图像全站仪快速天文测量中星点轨迹研究
张 旭,张 超,李华孝杨,路 辉,2
(1.信息工程大学,郑州 450001;2.96766部队,河南 信阳 464000)
天文测量是通过观测天体来确定地面点的天文坐标或两点间天文方位角的观测方法,是一种可靠性高、实用性强、隐蔽性好的定位定向方法,在所有定向测量中精度最高[1]。短时间内实现快速天文定向,确定地面目标天文方位角技术在航海、野外盲测、无路径导航等领域有诸多的应用[2]。
天文测量正在朝智能化、快速化的方向发展。传统天文观测通过人眼获得目标,人仪差不可避免,使天文测量的精度和效率下降[3]。20世纪80年代CMOS(Complementary Metal-Oxide-Semiconductor)传感器诞生之后,CMOS成像技术得到快速发展。CMOS技术引入到天文测量仪器,可实现自动化、智能化观测,消除人仪差的影响,真正在短时间内实现快速天文观测。对于无穷远处的恒星来说,短时间内在地球上观测到的相对角运动平均速度为15″/s,搭载CMOS传感器的图像全站仪具有1.5°视场角,研究短时间内星点轨迹,预测星点下一时刻在视场中的大致位置,实现星图的快速处理。
短时间内星点轨迹的研究对快速天文测量具有重要作用。最常用的三角形星识别算法,需要对多颗星连续观测,外推同一时刻下各恒星的方位信息,研究短时间内星点运动可以合理把握观测时间,建立正确外推模型[4];此外,研究星点轨迹可预判星点在视场中的大致位置,不仅可实现不转动仪器的前提下连续观测亮星,还便于缩小星图处理区域,快速提取星点质心像素坐标[5-6]。文中从几何模型理论推导和实测数据最小二乘拟合两个方面,分析短时间内连续观测亮星的轨迹,并给出符合最佳拟合效果的时间范围,为精密天文测量中单颗星观测时长提供参考。
1 图像全站仪快速天文测量
1.1 基于CMOS图像全站仪的天文测量
基于CMOS传感器的图像全站仪促进了天文测量的发展。互补金属氧化物半导体(CMOS)是制造大规模集成电路芯片用的一种技术,这种技术制造出来的芯片,也被用于制作数码影像器材的感光元件,又被称为CMOS光电影像传感器。相较于CCD传感器,CMOS传感器具有低功耗、抗辐射能力强、动态范围大、读出速度快、成本低、成品率高等优点[7]。因此,提高工作效率的同时降低数据转移的风险和工作成本,数据也可永久保存,这些优点用于全站仪恰好能改进传统天文测量仪器方面的不足[8]。
目前,CMOS传感器在图像全站仪精密天文测量中广泛使用。将CMOS传感器引入全站仪进行天文观测,可建立相对稳定、准确的转换关系,计算时只需准确客观的转换公式就可替代人眼观测,避免校准计算[9];相较于传统天文测量仪器,图像全站仪有稳定的自动转台,在计算机控制下,利用CMOS传感器拍摄亮星可使两星之间只需间隔在5 s以内,大大提高观测速度;另外,将CMOS传感器引入到测量仪器中,可以短时间内获取恒星的图像信息,所获得的图像无需打印处理可以直接在计算机上自动处理、分析、计算;基于CMOS传感器成像方法,获取拍照时延更加精确,可提高天文观测的精度。发挥CMOS图像全站仪的优势,可实现自动定位恒星和快速天文定位定向。
1.2 CMOS相机坐标与全站仪坐标之间的转换
CMOS相机内置于全站仪,两者固定成统一的刚体,但两者之间并不完全重合,CMOS相机坐标系(o-xcyczc)与全站仪坐标系(O-ZYX)之间存在差异(见图1),在测量之前要先确定两个坐标之间的转换参数。其中包括:相机投影中心在全站仪坐标系中的3个位置偏移量(Δx,Δy,Δz),像空间坐标系和全站仪坐标系的3个旋转角(φ,ω,κ),以及坐标系比例尺转换系数m。这7个参数也被称为相机相对于全站仪的姿态偏移参数OFFSET。

图1 坐标转换图
(1)
其中,(X,Y,Z)表示物点在全站仪坐标系下的坐标,Rφωκ表示xc,yc,zc3个方向的旋转矩阵,(x,y,z)表示物点在CMOS相机坐标系下的坐标。通过提前获得参数,对星点拍照时每张图像的OFFSET是一样的,只需标定坐标转换数学模型,发挥CMOS芯片的优势,达到图像实时处理和快速获取数据的目的[10]。
2 短时间星点轨迹分析
2.1 几何模型法
亮星在夜空中运动,短时间内在地球上观测到的平均相对角运动为15″/s,其运动轨迹模型如图2所示。
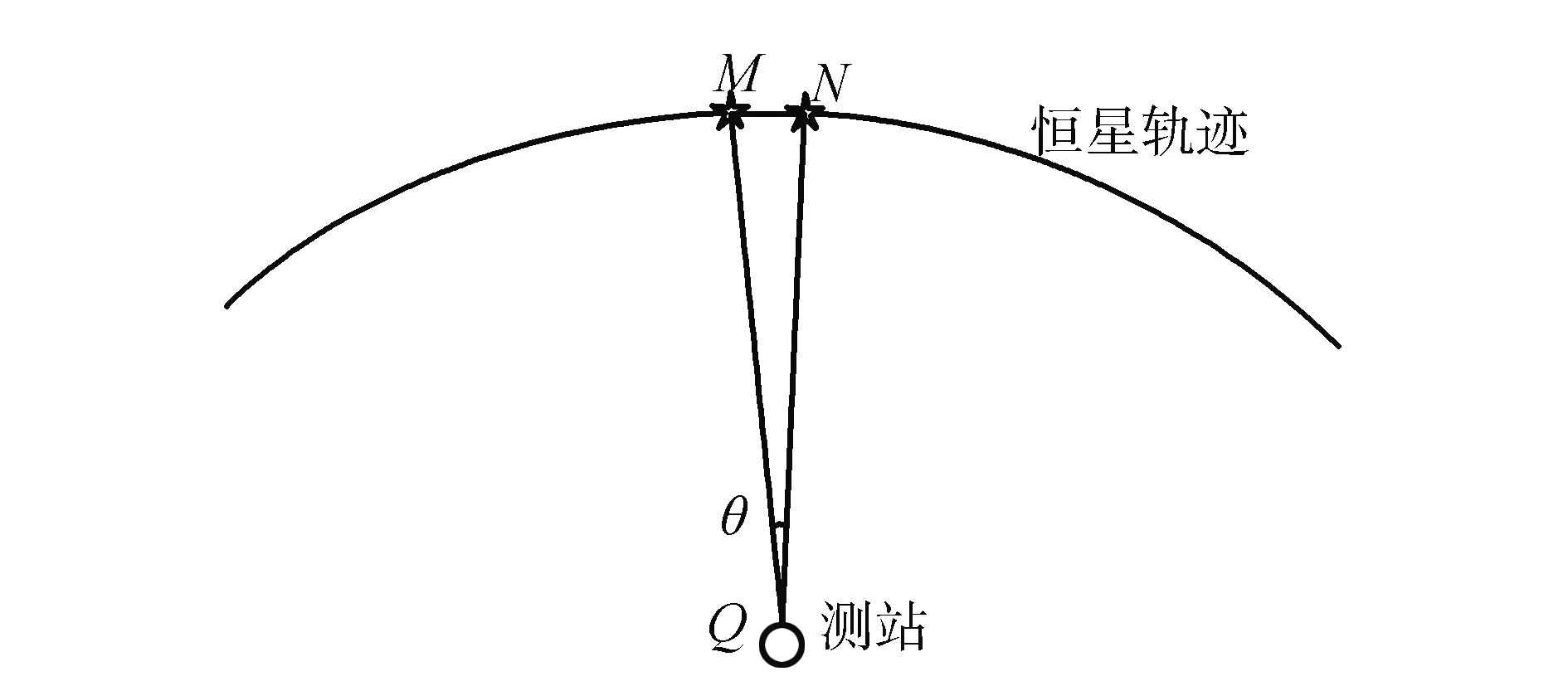
图2 星点轨迹模型
其中,M,N为亮星轨迹上的两个点,Q为MN间的角距,Q点为地球上的测站,由于地球距离亮星的距离为无穷远,设距离为R=1。由圆弧计算式和三角形计算关系可知:
(2)

(3)
其中,Rn(x)为拉格朗日余项,ξ为0与x之间的不确定值。由于θ的值较小,取n=2,有:
(4)
令cosξ=-1使得Δθ取最大,则:
(5)

2.2 最小二乘曲线拟合法
数学原理拟合星点轨迹。CMOS图像全站仪连续获取星点的图像信息,若每颗恒星拍摄n次,经图像处理和星点提取,获得n组亮星在地平坐标系下的水平角和高度角,令观测时间x和水平角或者高度角组成坐标(x1,y1),(x2,y2),……,(xn,yn),之后对坐标进行k阶多项式最小二乘拟合。
(6)
这些多项式对应的曲线不一定可以拟合所有点。因此,需计算出满足式(7)的一组系数。
(7)
由式(8)对a0,a1,a2,…,ak求偏导,并令其为0求解所有系数的值。
(8)
对此范德蒙矩阵继续分解,令:
则式(8)可以分解为:XTXa=XTY,可得到a=(XTX)-1XTY,求出各参数的系数。由实验数据,利用最小二乘方法拟合不同阶次的曲线,计算系数。比较不同阶曲线的拟合效果和残差平方和,得出最为符合星点轨迹的曲线拟合方式。
3 实验设计与数据分析
3.1 实验设计
2020年8月10日晚20时,在我国华北地区某固定测站采集天文数据。采用测角精度为±0.5"的徕卡TS60图像全站仪,粗瞄范围广,精瞄准确度高;搭配Y/JGT-01天文测量系统,具体观测条件如表1所示。

表1 观测条件
3.2 数据分析
星点观测数据经过处理,可以更好展现星点运行轨迹。图3是从所有观测亮星中任取1颗,将其8次图像像素叠加,从图中可看出星点轨迹大致呈直线型。

图3 星点轨迹像素叠加图
从观测数据分析,任选其中4颗亮星,每颗星的8张图像经图像处理后获得一组水平角、高度角的时间序列,分别将两个方位角的时间序列与观测时间进行不同阶最小二乘拟合,计算各拟合方式的均方根误差,如表2所示。由表中的数据可知,显然一次拟合的精度更高,且计算复杂度更低,也说明短时间星点轨迹线性拟合为最佳拟合的准确性。

表2 任意亮星多种拟合残差平方和 (″)
另外,为研究拟合时间跨度对拟合精度的影响,将16个时段中所观测的192颗星的方位角时序随机选取时间范围完成一次最小二乘拟合,并计算拟合的均方根误差,如图4所示,由于其他因素的影响,包括仪器观测误差、人仪差、星、温度等外界观测条件的变化,使得相同拟合时间的均方根相互之间存在差异,但绝大多数分布在一定精度范围内[11]。

图4 192颗星方位角时序随机拟合均方根误差
另外,从图4中发现相同拟合时间存在几个互差较大的孤点,人工剔除孤点后,计算相同拟合时间均方根的平均值,如图5,随着拟合时间跨度的增加,均方根呈现上升的趋势,且拟合时间不超过60 s时,均方根误差不超过1″,验证短时间星点轨迹线性拟合的可靠性,为天文测量中快速星点处理提供有价值的参考。
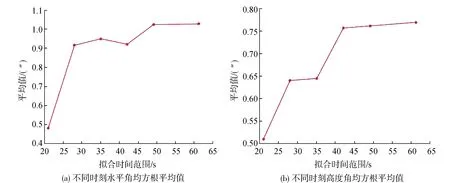
图5 不同时间跨度的方位角时序拟合均方根平均值
4 结束语
从几何模型中推导短时星点运动轨迹特征,之后建立数学模型并结合实测数据,将星点的方位角时序与观测时间多阶拟合,验证短时星点轨迹时序线性拟合的准确性。在此基础上,对观测亮星随机划分时间跨度拟合方位角时序,极大清晰地说明该结论的可靠性,且拟合时间跨度小于60 s时,均方根误差不超过1″。文中的研究不仅对图像全站仪应用于天文测量具有重要意义,且根据该理论可预测亮星下一时刻的位置,以缩小星图处理的范围,从而加速星点质心的提取速度。另外,观测者可控制合理的观测时间,以满足高精度的天文测量。

