空气静压型快刀伺服系统的流体动力学仿真分析

陈向阳，周 猛,邹喜聪

(黑龙江大学 机电工程学院，哈尔滨 150080)

0 引 言

基于快刀伺服系统的超精密加工方法具有加工精度高、表面质量好、加工效率高等特点，被广泛应用于自由光学曲面元件的加工与制造[1]。快刀伺服系统的驱动单元主要包含压电陶瓷和音圈电机两种形式[2]。以压电陶瓷为驱动单元的快刀伺服系统的工作响应频率较高，可达几十kHz，但其工作行程较短，一般在100 μm以内，不适用于加工具有较大深宽比的自由光学曲面元件[3]。而以音圈电机为驱动单元的快刀伺服系统在保证高频响的同时兼顾了大行程的特点，可实现毫米级行程，在渐进式多焦点镜片等较大深宽比的零部件加工制造方面具有不可取代的优势[4]。因此，以音圈电机为驱动单元、以空气静压导轨为导向机构的空气静压型快刀伺服系统成为自由光学曲面元件生产制造领域内不可或缺的重要装置。空气静压导轨的承载力、刚度以及导轨间隙内气体压力的分布情况是影响空气静压型快刀伺服系统性能的重要指标，其承载力和刚度特性直接影响着快刀伺服系统的运动稳定性和最终的加工质量[5-6]。

以自主设计的空气静压型快刀伺服系统作为研究对象，建立空气静压导轨的气体润滑基本方程，推导三维稳态Reynolds方程，获得空气静压导轨的承载力和刚度方程。通过FLUENT软件进行CFD仿真，研究空气静压导轨的供气压力、气膜厚度与承载力、刚度的影响关系。

1 快刀伺服系统结构设计与理论分析

1.1 快刀伺服系统整体结构

空气静压型快刀伺服系统主要包括驱动部分、导向部分及位置反馈系统等。驱动部分以音圈电机作为核心驱动单元，通过改变音圈电机的输入电压实现定子和动子之间的相对运动，不需要中间传动机构即可实现线性移动；导向部分以空气静压导轨作为导向机构，导轨与溜板之间利用压缩空气进行润滑，可达到接近零摩擦的效果，同时具备较高的系统刚度；位置反馈系统以直线光栅尺作为核心反馈单元，通过读数头的读取和细分实现高精度的位置反馈和闭环控制。

1.2 空气静压导轨

空气静压导轨采用气体静压润滑技术，具有摩擦力小、动态特性好、承载力强、刚度大等特点。空气静压导轨的三维模型见图1。由图1可见，上溜板、下溜板以及左右两个侧溜板共同合围形成矩形空间，导轨置于溜板围成的矩形空间并可在其内部进行平稳运动。各溜板内表面嵌有节流孔，高压空气从节流孔流出后在各溜板和导轨之间形成气膜，从而实现气体静压润滑。

图1 空气静压导轨结构

表1 节流器设计指标

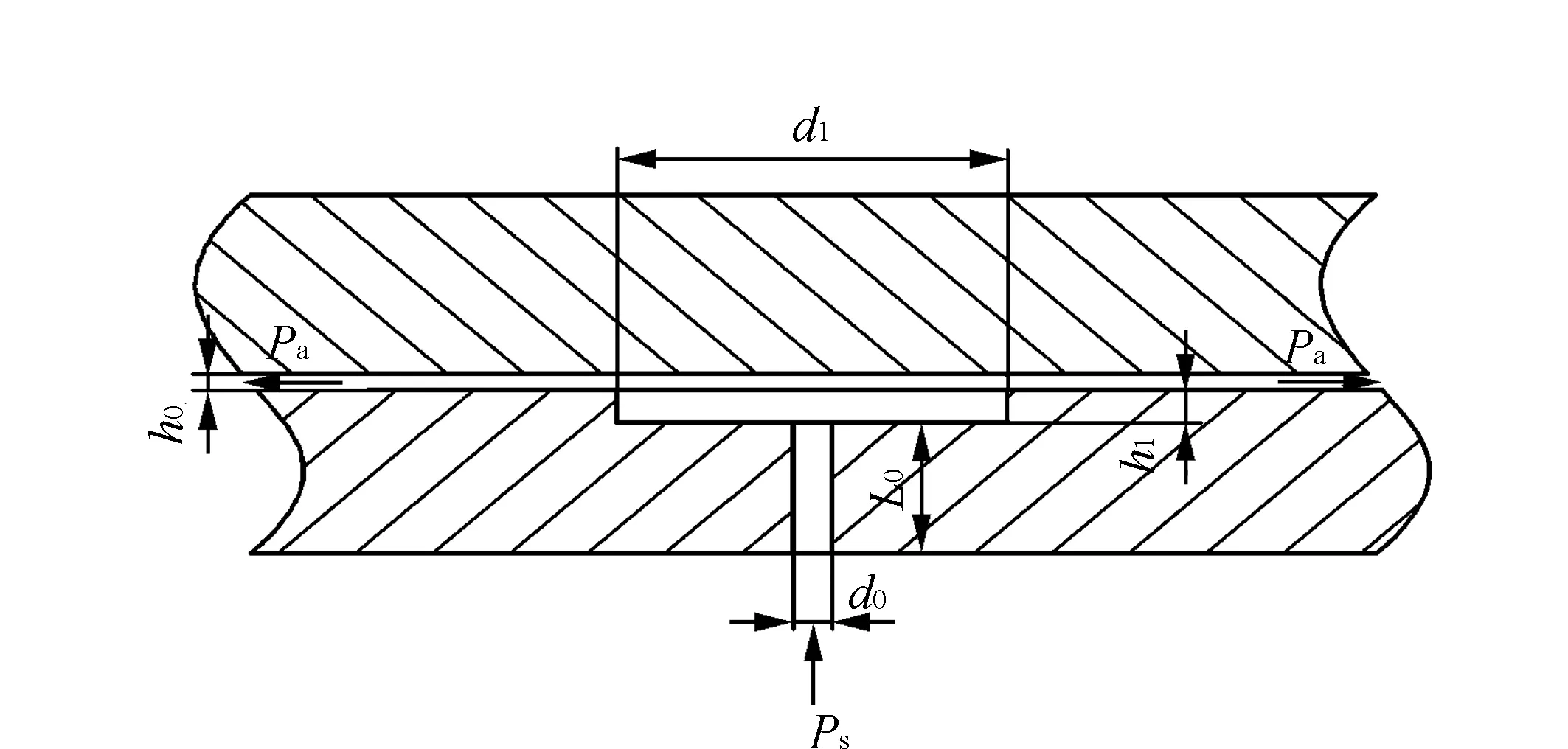
图2 节流器结构

各溜板内表面上的节流孔分布见图3，溜板和导轨之间的气膜流体域尺寸a×b为80 mm×40 mm，节流孔双排均匀排布，每排4个节流孔，横向、纵向间距c均为20 mm，有效气浮面积3 030.35 mm2，设计气膜厚度为15 μm。

图3 空气静压导轨流体域

2 气体润滑基本理论

2.1 气体润滑基本方程

气体润滑基本方程是指将质量、动量和能量守恒定律用于流体运动所得到的关于流体速度、压力、密度和温度等物理量的关系式，主要有连续方程、动力学方程和状态方程。

2.1.1 连续性方程

任意流体微团的流动都必须满足质量守恒定律，根据此定律可得到质量控制方程[7]为

(1)

式中:ρ为流体密度(kg·m-3);t为时间(s);vx为x方向的速度分量(m·s-1);vy为y方向的速度分量(m·s-1);vz为z方向的速度分量(m·s-1)。

空气静压导轨的气体流速较低，可视为不可压缩的恒定流动，即密度ρ为常量，因此，式(1)可改写为

(2)

2.1.2 动力学方程

动量守恒是流动动力学系统须满足的基本定律之一，动力学方程是根据动量守恒定律演变而来的控制方程。

空气静压导轨的气膜厚度与空气静压导轨结构尺寸相比要小不止一个数量级，因此可对空气静压导轨的气膜进行以下假设：①气膜厚度很小，可忽略与气膜相垂直方向上的气体流速和压力；②不计惯性力等体积力的影响；③气体润滑过程视为等温过程，黏性系数为常数；④气膜流体域中气体的流动为层流。

基于以上假设，空气静压导轨中气体可视为定常流，流体域内部沿y方向的压强P与坐标无关，简化后的动力学方程为

(3)

式中：P为气体压强(Pa);η为气体黏性系数(Pa·s)。

2.1.3 状态方程

状态方程一般表达式为

P=ρRT

(4)

由于空气静压导轨的两侧润滑面都是金属，导轨产生的热量大部分能传递出去，因此气体润滑可视为等温状态，状态方程可写为

P/ρ=Pa/ρa

(5)

2.1.4 Reynolds方程

从仿真分析角度而言，计算流体力学的本质是求解气体润滑的雷诺方程，气体润滑雷诺方程可由气体等温条件下连续性方程和动力学方程推导求得。

联立连续性方程式(2)、动力学方程式(3)、状态方程式(5)，并考虑速度边界条件、压力边界条件和对称边界条件等，可得到空气静压导轨的雷诺方程为

(6)

式中:vx0为x方向速度分量在y坐标为0时的速度值(m·s-1)；vxh为x方向速度分量在y坐标为h时的速度值(m·s-1)；vz0为z方向速度分量在y坐标为0时的速度值(m·s-1)；vzh为z方向速度分量在y坐标为h时的速度值(m·s-1)。

空气静压导轨中气膜表面可近似看成刚体，即

(7)

则雷诺方程可简化为以下偏微分方程形式

(8)

2.2 承载力和刚度方程

承载力W和刚度K是用来表征空气静压导轨的静态性能的主要参数。承载力是由导轨流体域浮力和大气压综合作用的结果，对气膜内的压力分布进行积分可以求得气膜承载力[8]

W=∬AP(x,z)dxdz-APa

(9)

式中：A为有效气浮面积(m2)；P(x,z)为节流孔中心压强(Pa)；Pa为大气压强(Pa)。

刚度是指气膜产生单位变形量时所能承受的载荷大小，考虑到求解的便利性，在满足计算精度的前提下，一般使用差分法进行刚度估算[8]。

(10)

3 CFD仿真分析

3.1 气膜三维模型

由于空气静压导轨的结构具有对称性，为了减少计算时的工作量,建立模型时进行简化处理，只抽取下溜板与导轨间的流体区域构建三维模型。利用SCDM软件模块建立，气膜三维模型见图4，气膜长度、高度和宽度方向分别为笛卡尔坐标系中的x、y和z轴。

图4 气膜流体域三维模型

3.2 网格划分及边界设置

对于计算流体问题，网格是一切计算的基础，网格质量很大程度上决定了结果的精确程度。因为空气静压导轨的长宽与厚度相差3个量级，比例失调，自动生成的网格质量不符合计算要求。因此使用ICEM软件手工划分气膜模型的网格，见图5，节流孔处为压力入口，气膜流域与空气相接触的部分为压力出口。

图5 气膜流体域的网格划分

“O”型网格划分方法是ICEM软件中特有的功能之一，“O”型网格最常使用于二维的圆、三维的圆柱、球形等横截面为圆形的几何模型的网格划分中。“O”型网格划分方法的基本原理是对圆截面进行分割，使其形成类似于方孔铜钱的外圆内方形状(如图5中压力入口处)并进行网格划分。在圆截面内创建一个几何中心与圆截面圆心重合的正方形；依次连接四边形的几何中心与4个顶点并延长到圆弧上，将圆截面均分成4等分；删除正方形内部的对角线，从而将圆截面分割成1个正方形和4个扇形区域。5个区域逐个进行结构化网格划分即可在圆截面内形成规则的四边形网格，沿圆柱体轴向上扫略即可生成规则的六面体网格。相比于常规面网格划分方法，“O”型网格可以优化网格纵横比、控制网格畸变、改善网格质量。“O”型网格的另一个优势在于可以很方便地施加边界层网格，“O”型网格与边界层扩展方向相一致，有利于网格质量的提升。

针对节流孔和气腔部分的形状特征，采用“O”型方法对节流孔处的流体进行网格划分，以避免形成网格畸变。由于节流孔和气腔的过渡处横截面产生急剧变化，气体流经此处后流速会陡然上升，速度梯度与压力梯度均较高，网格密度需要相应升高，因此采用渐进加密的方式提升密度，增长率设置为1.1。最终得到172 182个网格单元。

对网格的Quality、Angle、Determinant和Warpage评测，Quality最大值为1，最小值为0.724，在0.95～1.00区间所占比重最大，接近50%；Angle最大值30°，最小值46.44°，在区间85.5°～90°内占比为71.488%；Determinant行列式最大值为1.0，最小值为0.861，95%以上分布在0.9～1.0区间；Warpage最大值为27.1°，最小值为0°，区间0～4.5°占比为98.303%。以上指标均符合Fluent求解器的求解收敛要求。

3.3 求解器、边界条件及控制参数的设置

采用FLUENT软件进行流体动力学仿真分析，求解器选择双精度三维压力求解器，气膜内的气体视为等温层流、不考虑黏性且流动方向保持一致。依据已知条件，入口采用压力入口边界，压力初值设置为0.5 MPa，出口采用压力出口边界，出口表压力设置为大气压力，气体流动方向规范方法是Normal to Boundary。求解算法采用基于速度与压力相互耦合原理的SIMPLEC。解决方案控制中压力、密度、体积力和动量的欠松弛因子分别设置为0.3、1、1和0.7。在迭代过程中，残差值均设置为1×10-6，使用标准初始化，从Inlet开始计算，迭代次数设置为1 500次，动态地监视计算的收敛性和当前的计算结果，当残差达到设定值1×10-6计算终止，此时认为计算结果的精度达到要求。迭代过程残差监视图见图6。

图6 迭代过程残差监视图

3.4 CFD仿真结果及分析

当节流孔供气压力为0.5 MPa，出口压力为大气压力时，空气静压导轨气膜的压力分布见图7。由图7可见，节流孔处是压力源，此处压力高于其他部位。中间区域的气膜不直接与外界相连，此处压力分布均匀，且压力值高于周围其他空间。气压从中间区域向外逐渐降低，到压力出口处时压强降至大气压。

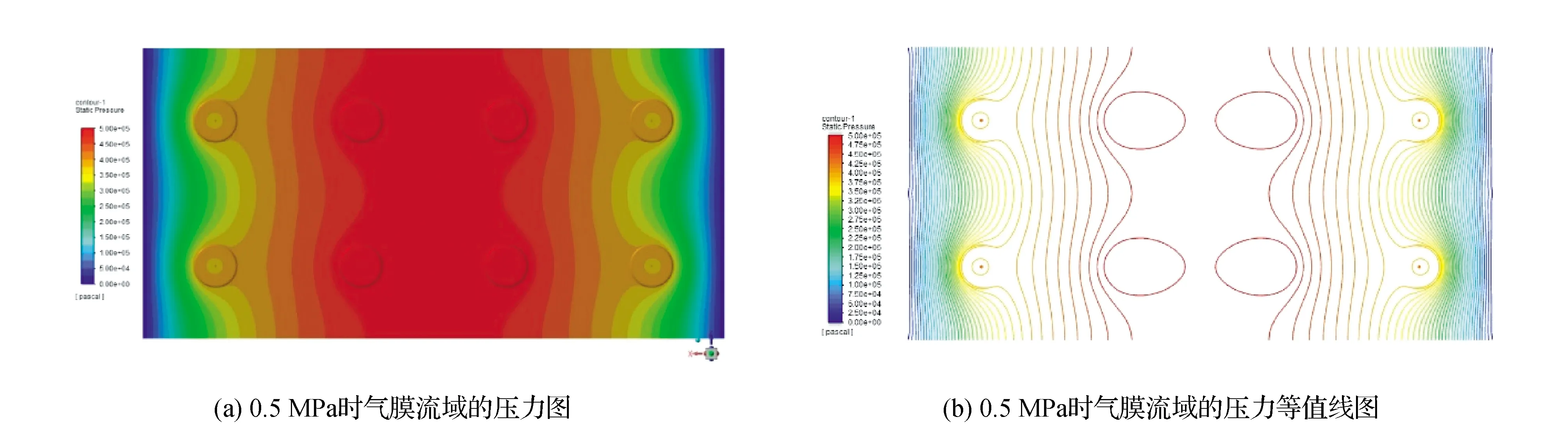
图7 0.5 MPa时气膜压力分布

3.4.1 节流孔气膜压力分布

沿x方向对节流孔进行依次编号1、2、3、4，气膜压力在x和z轴的分布见图8。由图8(a)可见，节流孔1处气膜沿z方向的压力分布，气膜压力在节流孔位置最高。由于气腔的存在，压力不再是从节流小孔出来后直接快速下降，而是存在一个压力相对稳定的均压阶段，并且因为气膜沿z方向不与大气相连，因此气膜两端压力最低值并不为零。由图8(b)可见，节流孔1处气膜沿x方向的压力分布，气膜左端与大气相通压力为零，右端由于2号节流孔的存在导致气膜压力上升。由图8(c)可见，4个节流孔处气膜沿x轴的压力分布，相较单节流孔，4节流孔中间两节流孔气膜压力值增加，压力分布从单一中心峰值过渡为4中心峰值。由图8(d)可见，8节流孔气膜压力三维分布图，节流孔数量的提升带来了更高的承载力。

图8 节流孔的压力分布

3.4.2 供气压力对承载力和刚度的影响关系

在气膜厚度不变的情况下，分别对供气压力为0.2、0.3、0.4、0.5、0.6 MPa进行了仿真模拟。当保持气膜厚度15 μm不变，仅改变供气压力的大小时，承载力和刚度也随之变化，见图9。气膜的承载力随供气压力的增加而增大，且基本上呈线性关系(图9(a))。气膜的刚度也随着供气压力的增加而增大(图9(b))。因此，适当增加供气压力，可以在一定程度上提高空气静压导轨的承载力和刚度。

图9 气膜厚度恒定时供气压力对承载力和刚度的影响

3.4.3 气膜厚度对承载力和刚度的影响关系

在供气压力不变的情况下，分别对不同气膜厚度进行了仿真模拟。当供气压力为0.5 MPa时，气膜厚度与承载力关系见图10(a)，承载力随气膜厚度的增加而下降，且下降速度逐渐加快，主要是由于随着气膜厚度增加，导轨内部的空间逐渐变大，气体压缩不够完全、对外压力降低，进而影响到气膜的承载力，与此同时气膜刚度却随气膜厚度的增加而增大，见图10(b)。为了揭示供气压力、气膜厚度对承载力和刚度的影响规律，在上述基础上进一步扩大仿真范围，对不同供气压力和不同气膜厚度进行仿真分析。

图10 供气压力恒定时气膜厚度与承载力和刚度关系

供气压力、气膜厚度对承载力的影响关系见图11。由图11可见，不同供气压力下，气膜厚度对承载力的影响关系基本一致：在气膜厚度为5～15 μm时，气膜厚度变化值对承载力的影响较小，而供气压力是影响承载力的主要因素，承载力随着供气压力的增加而增大；当气膜厚度为15～30 μm时，承载力随着气膜厚度的增加而快速下降，此时供气压力和气膜厚度共同影响着承载力；当气膜厚度大于30 μm后，承载力随着气膜厚度的增加而缓慢下降，但其下降速度有所放缓，此时供气压力不再是影响承载力的主要因素。

图11 不同供气压力、气膜厚度对承载力的影响关系

供气压力、气膜厚度对刚度的影响关系见图12。由图12可见，不同供气压力下，气膜厚度对刚度的影响关系也基本一致，随着气膜厚度的逐渐增大，刚度呈现先增加后减小的趋势，刚度的极值出现在气膜厚度15～25 μm，在此厚度区间内，刚度随着供气压力的增加而变大，表明除气膜厚度外供气压力也会对刚度产生较大影响；当气膜厚度较小或较大时，气膜刚度均趋于零，此时气膜抗干扰能力弱，无法为空气静压导轨提供充分的抗干扰能力。

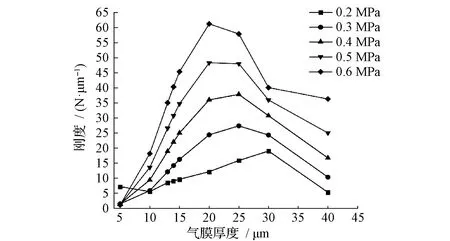
图12 不同供气压力、气膜厚度对刚度的影响关系

综上所述，供气压力恒定时，随着气膜厚度增加，承载力降低而刚度先增加后减小；气膜厚度恒定时，承载力和刚度都随着供气压力的增加而增加。当空气静压型快刀伺服系统需要较大承载力时，气膜设计厚度应为5～15 μm，同时也要适当增加供气压力；当需要较大刚度时，除了要增加供气压力外，还需将气膜厚度控制在15～25 μm之间，以便获得最强刚度。

4 结 论

本文针对空气静压型快刀伺服系统进行了空气动力学和结构力学仿真，讨论了供气压力、气膜厚度对承载力、刚度的影响规律，可得到如下结论：

1)当气膜厚度不变时，承载力和刚度随供气压力的增加而上升，而且呈线性正相关；当供气压力保持不变时，承载力随气膜厚度的增加而下降，刚度随气膜厚度的增加先上升后下降。

2)承载力和刚度两者极大值所对应的气膜厚度并不完全相同，为了获得较强承载力和刚度，气膜设计厚度一般应为15～25 μm，此时适当提高供气压力有益于提高承载力和刚度。