悬挂式有轨制导车辆车体多目标参数优化设计

□ 陈 思 □ 李成群

华北理工大学 机械工程学院 河北唐山 063210

1 优化设计背景

当前,物流仓储技术不断发展。悬挂式有轨制导车辆作为新型搬运设备,不仅能够满足高效物流搬运作业的需要,而且对环境的适应性更强,改变了传统人工作业模式,提高了仓储空间的利用率[1-2]。

悬挂式有轨制导车辆车体的质量和力学特性对搬运系统整体性能和功能有至关重要的影响。在承受既定载荷和给定约束的前提下,对悬挂式有轨制导车辆进行合理的结构布局和尺寸参数优化,通过计算机分析,得到最优的结构方案[3]。洪求才等[4]在对车架进行优化时,既保证了车架的动态特性和强度要求,又达到了轻量化的设计目的。Zhang Ran等[5]在对电动车进行优化时,结合灵敏度分析法提高了优化效率。

笔者对悬挂式有轨制导车辆车体进行多目标参数优化设计,选择满载工况进行分析,结合灵敏度分析、响应面分析、模态分析,在满足轻量化设计原则的前提下,优化车体框架尺寸和结构分布,提高悬挂式有轨制导车辆的整体性能,以达到车体性能最优化。

2 结构

对悬挂式有轨制导车辆车体进行静态分析,可以得到车体框架的变形和应力分布,针对结构的薄弱环节进行设计参数优化与改进,以提高车体结构的可靠性[6]。

悬挂式有轨制导车辆主要由车体、动力牵引单元、升降驱动单元、机械夹紧单元、导向单元、基础控制装置等组成。其中,车体结构如图1所示。

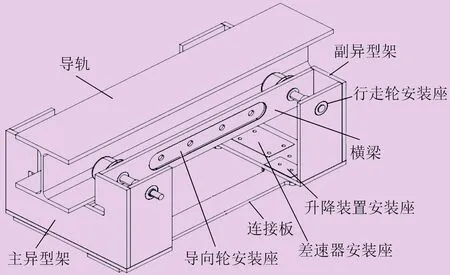
图1 车体结构

车体结构及性能特点如下:

(1) 车体主要基于两个由Q235B碳素结构钢焊接而成的异型架、一对连接横梁、两个对称连接板通过螺栓连接而成;

(2) 主异型架、副异型架上分别有横梁、连接板,以及升降驱动单元和机械夹紧单元的安装孔;

(3) 横梁上设有对称导向轮装置,使有轨制导车辆在单轨上能够正常行驶并及时导向,进而可以避免侧翻;

(4) 动力牵引单元及基础控制装置安装于车体内部,充分利用结构空间。

3 力学性能分析

应用CREO软件创建悬挂式有轨制导车辆车体参数化三维数学模型,同时配置CREO软件与ANSYS软件的数据接口,将参数导入ANSYS Workbench软件[7]。定义车体的材料为Q235B碳素结构钢,选择SOLID 185单元进行网格划分,网格尺寸为5 mm,共划分得到817 226个节点和362 324个单元。

考虑悬挂式有轨制导车辆最大负载时的接触与受力情况,选择超常载荷弯曲工况进行静力学性能分析与后处理。限制四个行走轮安装座位置的所有自由度,车体所受载荷主要由货箱、差速器、升降驱动单元、导向轮等部件的质量,以及车体自身质量组成。车体所受载荷与约束如图2所示。

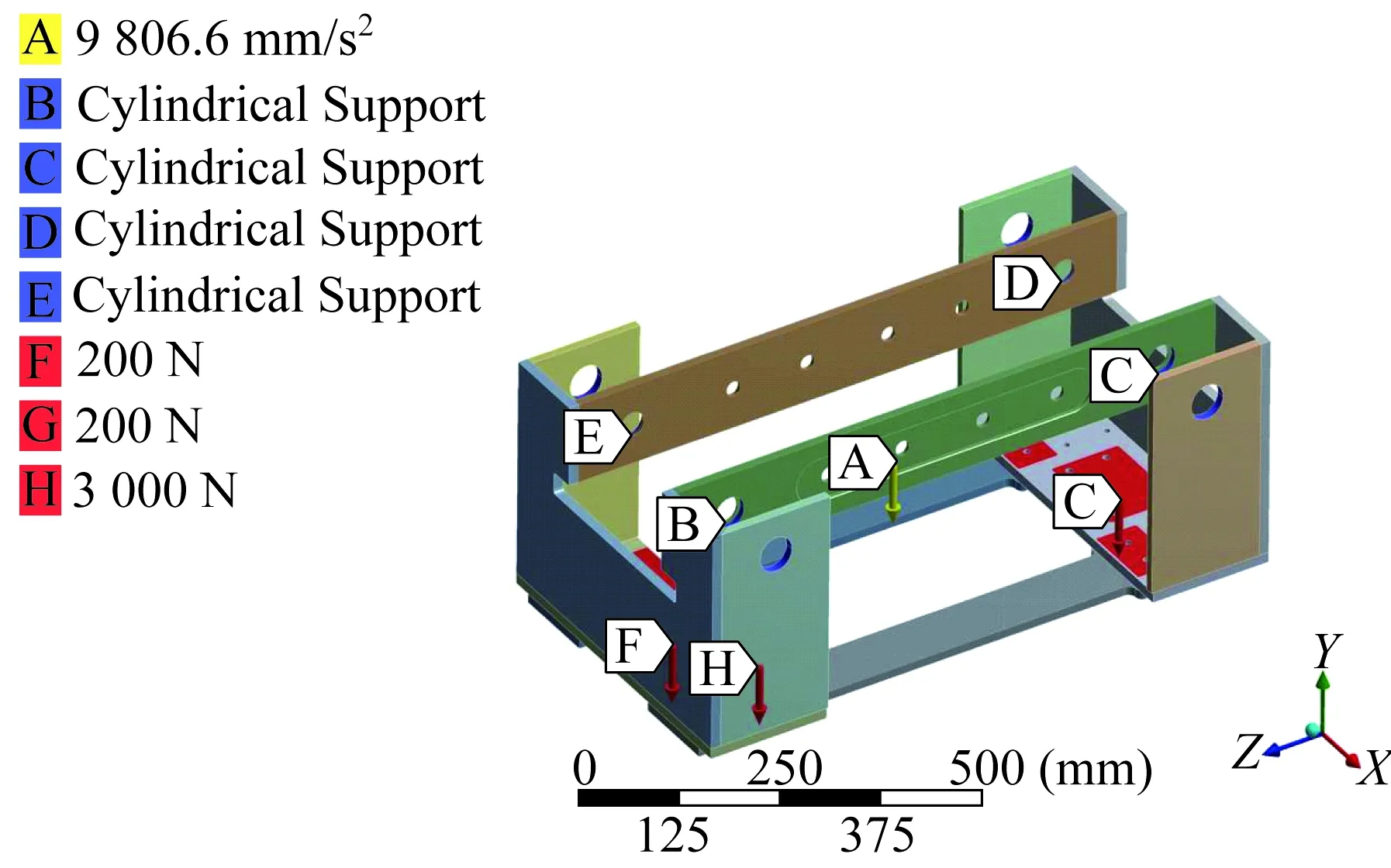
图2 车体载荷与约束

对车体进行静强度分析,车体的变形云图和等效应力云图分别如图3、图4所示。从图3中可以看出,车体最大变形产生于底部两连接板内侧中间部分,最大变形量为3.365 4×10-2mm,远小于1 mm。从图4中可以看出,车体最大等效应力产生于异型架底部两侧位置,最大等效应力值为9.873 3 MPa,远小于Q235B碳素结构钢的屈服强度235 MPa。

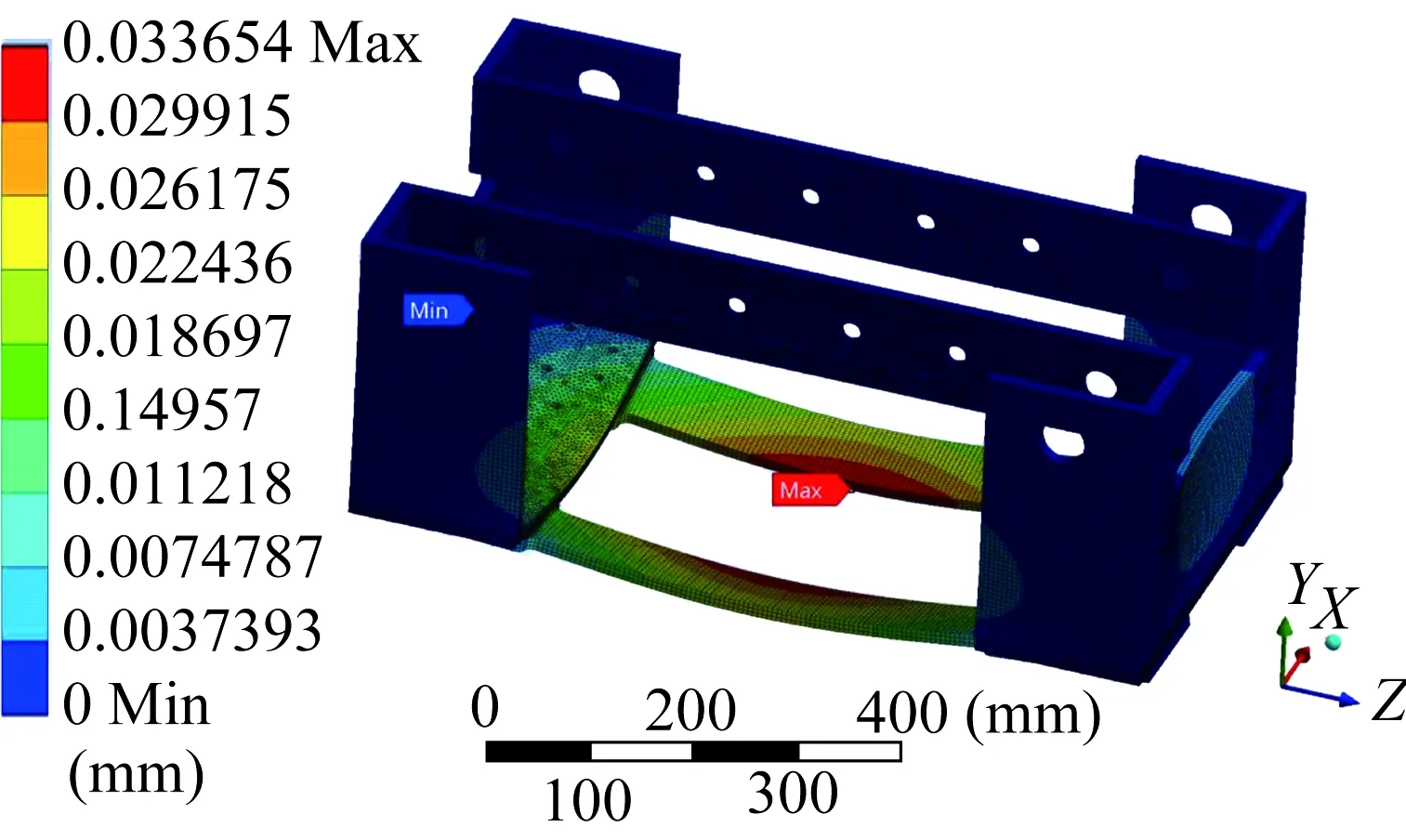
图3 车体变形云图

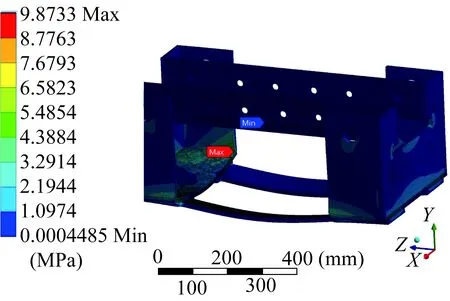
图4 车体等效应力云图

对车体进行模态分析,得到车体的前六阶模态频率和前三阶固有频率所对应的振型、最大变形。车体前三阶模态振型如图5所示,车体前六阶模态频率和最大变形量见表1。从图5、表1中可以看出,车体的一阶固有频率为232.45 Hz,远高于轨道的激励频率,轨道的激励频率低于100 Hz[8]。由此可见,能够避免悬挂式有轨制导车辆在搬运过程中发生共振现象,使悬挂式有轨制导车辆具有较高的稳定性与可靠性。

综合以上分析可以看到,车体的变形和等效应力均有较大的设计余量,且结构稳定,安全因数较高,有较大的优化设计空间。根据轻量化设计原则,可以考虑减小异形架组焊板截面尺寸,简化车体结构,在保证车体稳定性的基础上进行优化设计。

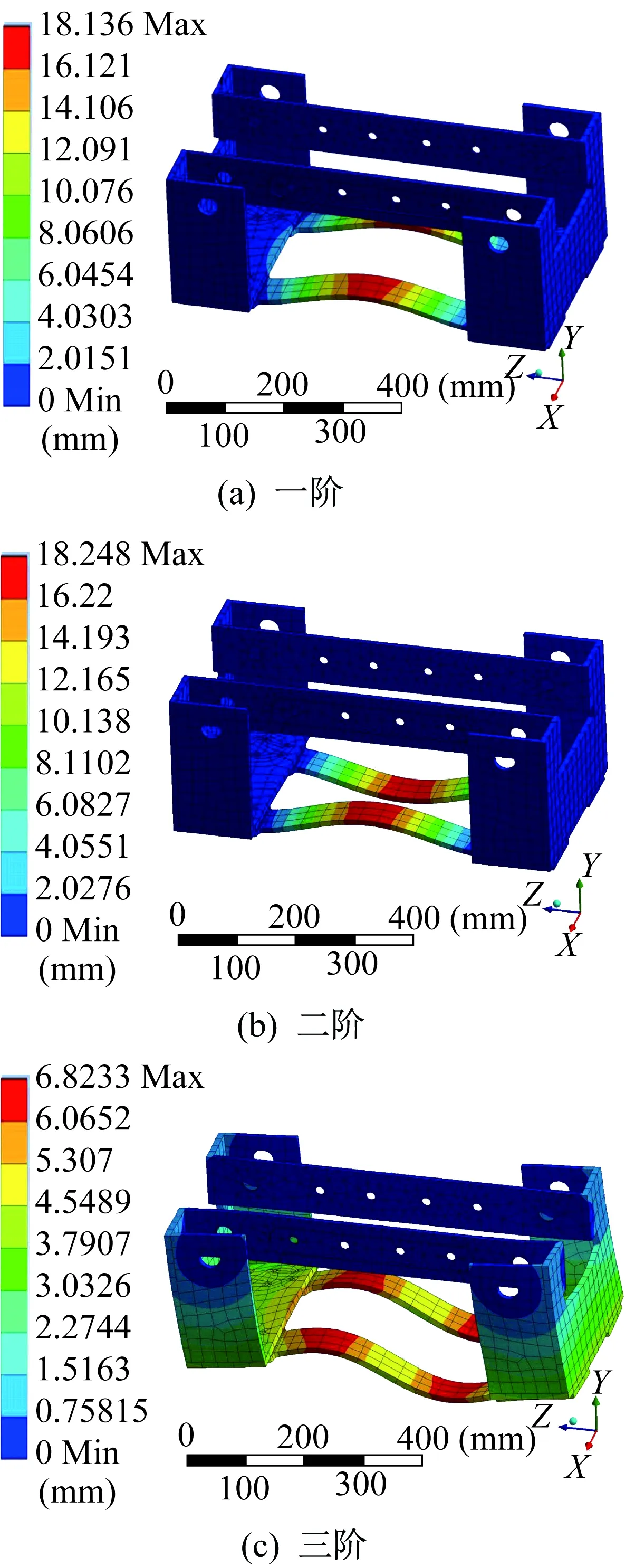
图5 车体前三阶模态振型

表1 车体前六阶模态频率和最大变形量

4 设计目标参数

在实际项目设计中,需要在物理模型中抽象出能够体现设计要求的一组数学表达式,即结构优化设计数学模型,主要包含设计变量、目标函数、约束条件三大要素[9]。数学表达式如下:

Findx=[x1,x2,…,xn]T

MinF(x)=f[x1,x2,…,xn]

s.t.Hj(x)=0j=1,2,…,k

Gi(x)≤0i=1,2,…,m

xia≤xi≤xibxi=1,2,…,n

式中:x为设计变量;n为设计变量数量;F(x)为优化目标函数;Hj(x)为等式约束条件;Gi(x)为不等式约束条件;xi为第i个所选设计参数;xia、xib分别为设计变量的上限、下限。

定义异型架底板厚度为P1,两侧板厚度为P2,连接板厚度为P3。根据上述静力学分析可知,车体框架的最大变形和最大应力分别产生在异型架的底板与侧板、底板与连接板的连接位置,异型架底板、两侧板、连接板的厚度对车体的变形和应力影响较大,因此将异型架底板厚度P1、两侧板厚度P2、连接板厚度P3设置为设计目标参数,如图6所示。

图6 设计目标参数

为减小车体变形量δ和应力σ,将车体质量M(x)、最大变形量δmax(x)、最大等效应力σmax(x)的最小值作为输出目标参数。其中,一阶频率f1(x)、二阶频率f2(x)、三阶频率f3(x)均需高于轨道的固有频率(100 Hz)[8]。将设计目标参数和输出目标参数代入前述数学表达式,建立目标参数优化数学模型:

Findx=[P1,P2,P3]T

MinF(x)=[M(x),δmax(x),σmax(x)]

s.t.M(x)=Mmin(x)

δ<δmax(x)

σ<σmax(x)

f1(x)>100

f2(x)>100

f3(x)>100

设计目标参数的取值范围见表2。

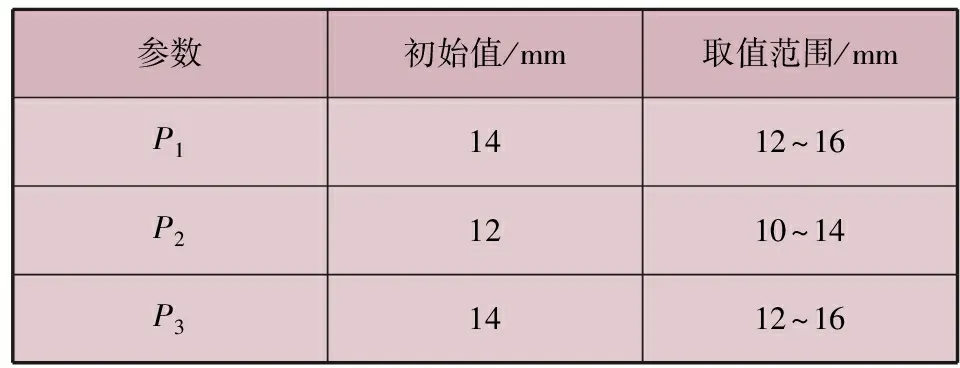
表2 设计目标参数取值范围

5 灵敏度分析

参数灵敏度分析是一种反映设计变量对目标变量敏感程度的分析方法[10]。在悬挂式有轨制导车辆车体参数优化过程中,需要对多个设计变量进行参数调整,以便找出对目标函数影响较大的关键设计参数。通过灵敏度分析,能够快速确定最为直接的主要设计变量。设计目标参数对目标函数的灵敏度分析结果如图7所示。由图7可以直观地看出优化过程中设计目标参数对车体质量、最大变形量、最大等效应力的相关程度、敏感因数、敏感程度。P1、P2、P3对车体质量的敏感因数依次为0.486 04、0.575 07、0.652 59,表明P3对车体质量影响程度较大,且呈正相关。P1、P2、P3对车体最大变形量的敏感因数依次为-0.877 49、-0.416 50、-0.250 55,表明P1对车体最大变形量影响程度较大,且呈负相关。P1、P2、P3对车体最大等效应力的敏感因数依次为-0.567 83、-0.675 53、-0.096 76,表明P1对车体最大等效应力影响程度较大,且呈负相关。

综合灵敏度分析可知,异型架底板厚度和连接板厚度对车体质量、最大变形量、最大等效应力影响较大,因此,在优化设计过程中要优先考虑选择较小值,这样有利于实现对悬挂式有轨制导车辆车体的结构优化与改进。

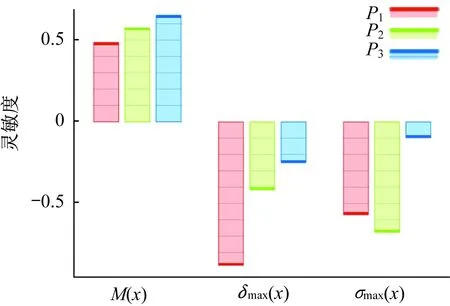
图7 灵敏度分析结果

6 响应面分析

响应面分析是一种能够准确反映输入参数与输出参数之间相互作用关系的分析方法[11]。针对悬挂式有轨制导车辆车体模型,通过响应面分析,拟合出输入的设计目标参数与输出的目标函数之间的响应关系曲面,能够更加直观地获得设计目标参数对目标函数的响应分布、响应趋势和每个设计点的响应。设计目标参数对车体质量、最大变形量、最大等效应力的响应依次如图8、图9、图10所示。

图8 设计目标参数对车体质量的响应

由图8可知,车体质量随P1、P2、P3增大而逐渐增大,其中P3对车体质量影响程度较大,P3应取较小值。

由图9可知,车体最大变形量随P1、P2、P3增大而逐渐减小,最大变形量远小于1 mm,因此,为使车体质量最小,这三个设计目标参数应尽可能选取较小值。

由图10可知,车体最大等效应力随P1、P3增大而减小,随P2增大先逐渐减小,当P2达到11.5 mm以后又逐渐增大。为减小车体最大等效应力,P2应选择为12 mm。

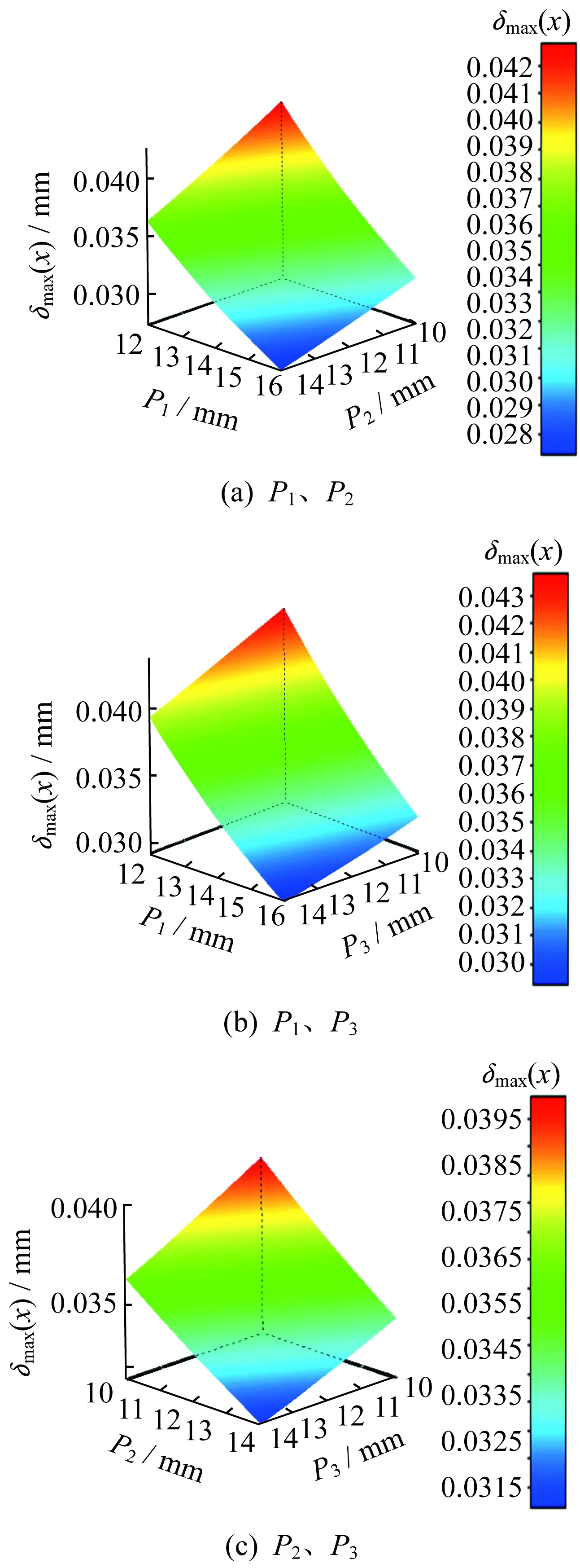
图9 设计目标参数对车体最大变形量的响应

7 候选方案

在满足所有约束条件的前提下,应用ANSYS Workbench软件DesignExplorer模块,根据优化设计数学模型,自动筛选出车体质量最小、最大变形量最小、最大等效应力最小的三组优化设计最大目标参数最优的候选方案,并对三个设计目标参数进行修正。候选方案见表3。由表3可知,三个设计目标参数优化后,使悬挂式有轨制导车辆车体总质量减小,车体最大等效应力有较小幅度增大,但未超出允许范围。综合上述分析可知,多目标参数优化设计不仅能够满足车体在强度和刚度方面的要求,而且使车体尺寸更加合理,优化效果显著。

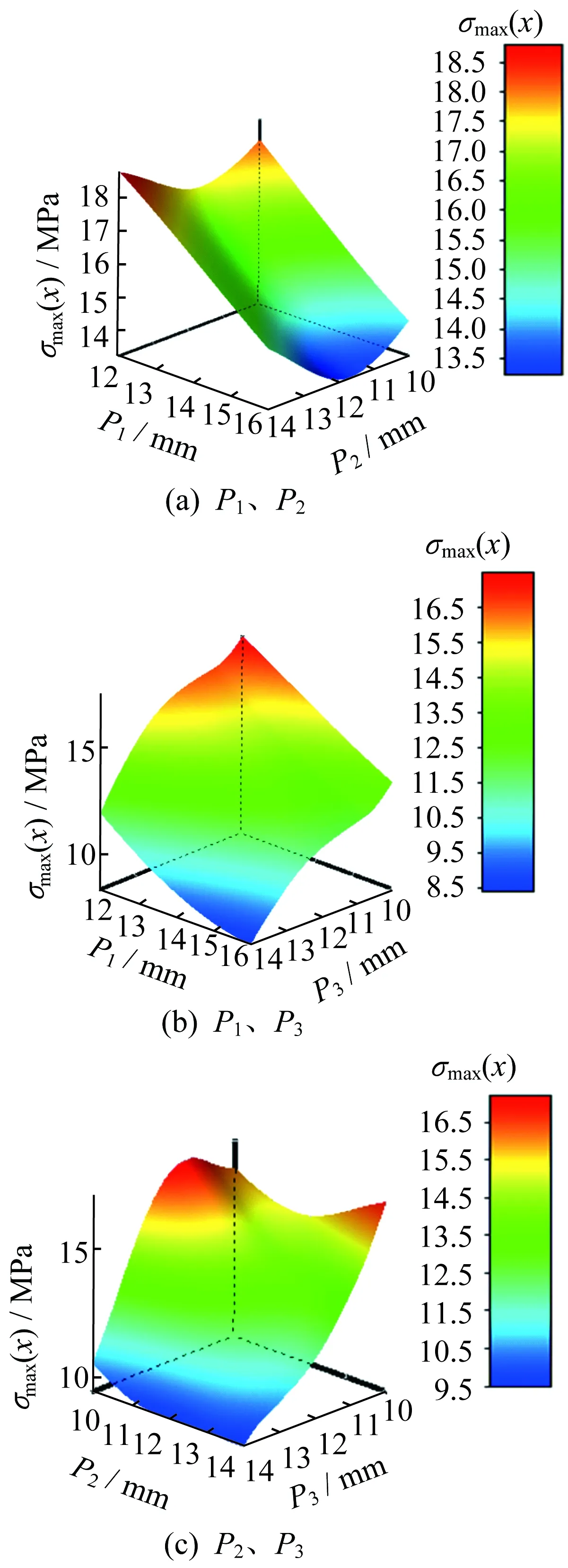
图10 设计目标参数对车体最大等效应力的响应

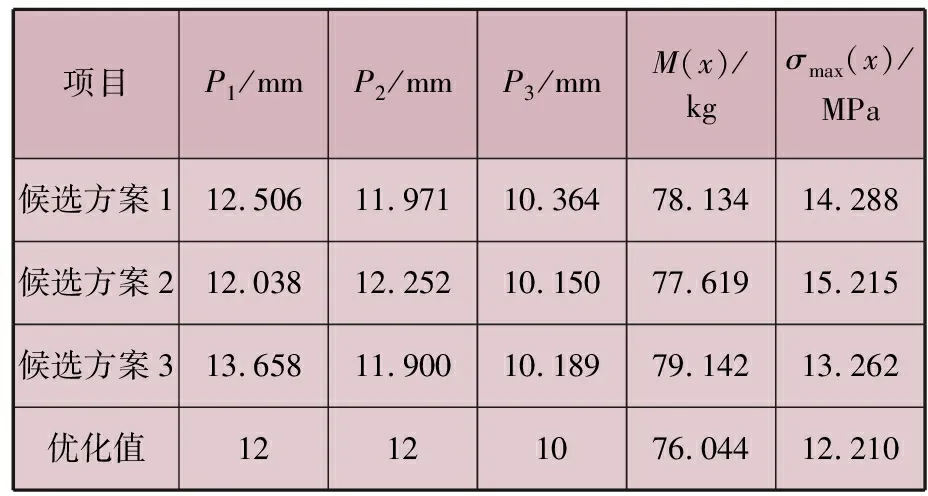
表3 候选方案

8 优化后车体性能评估

将确定的优化值输入ANSYS Workbench软件,应用DesignExplorer模块在相同的约束和载荷条件下再次进行静力学分析,得到优化后悬挂式有轨制导车辆车体与原车体的力学性能对比,见表4。

表4 车体力学性能对比

由表4可知,优化后车体质量较原车体质量减小了11.53%,轻量化效果显著。最大等效应力增大了23.67%,但仍远小于材料的屈服极限235 MPa,力学性能显著提升。一阶固有频率降低了3.24 Hz,且仍远离轨道的固有频率,在运行过程中可以有效避免共振发生,保证悬挂式有轨制导车辆运行的可靠性。

9 结束语

通过CREO软件与ANSYS软件建立数据接口,对悬挂式有轨制导车辆车体进行多目标参数优化设计,由静力学分析、模态分析、灵敏度分析、响应面分析得到车体关键尺寸与车体质量、最大变形量、最大等效应力间的关系曲线,通过筛选得到优化方案。优化方案与原车体对比,车体质量减小了9.908 kg,减小幅度为11.53%,轻量化效果显著。最大等效应力增大为12.21 MPa,但仍远小于材料的屈服极限。多目标参数优化设计使车体的结构和尺寸更加合理。