改进Census 立体匹配算法研究综述

宋培玉，王 森

（华东交通大学理学院，江西 南昌 330013）

立体匹配技术可以获得图像的深度信息，近年来受到了广泛的关注。 双目立体匹配的基本原理即模拟人的双眼，从两个视点观察同一场景获得两幅视图，根据两幅视图的像素点构建相似三角形计算两幅视图的视差获取深度信息。 自20世纪80 年代Marr 首次提出完整的机器视觉理论框架[1]。 曾文献等[2]对立体匹配算法进行了总结，描述了立体匹配算法的基本原理及立体匹配算法的分类。 陈华等[3]描述了立体匹配算法的基本步骤及各个立体匹配算法定性和定量的对比。 曹之乐等[4]总结了立体匹配算法的优缺点并对算法进行了深入的讨论和研究。 陈炎等[5]将立体匹配算法基于深度学习和人工特征进行了总结。 赵晨园等[6]分析了全局、半全局、局部、深度学习立体匹配算法的现状及不同算法的效果。 立体匹配技术不仅在医疗诊断、三维重建领域具有广泛的应用，而且可以准确、快速的识别障碍物信息，找出最优路径[7]。 但是，快速地得到图像的准确信息与立体匹配算法密切相关[8]。 全局立体匹配算法虽然可以得到较为精确的深度图，但是由于硬件设备要求高，计算复杂、实时性较差，一般采用局部立体匹配算法。 局部立体匹配算法主要是基于非参数变换和灰度相关性进行匹配。 常见的局部代价及算法包括灰度绝对值算法AD（absolute differences）、归一化互相关NCC（normalized cross correlation）[9]、去均值归一化互相关ZNCC（zero mean normalized cross correlation）[10]、 互信息MI（mutual information）、梯度法。AD 算法在计算匹配代价时对弱纹理区域误差较大； 同时NCC 算法在计算弱纹理区域和重复纹理区域时， 由于方差和均值变化不明显会导致误匹配； 基于梯度计算代价值在梯度不连续区域精度有所提高， 但对于光照的改变不敏感会导致误差较大。 基于灰度变换算法求视差图时， 由于噪声的影响使得到的视差图不平滑， 因此在实际应用中常使用由Ramin Zabih 和John Woodfill 等[11]提出的基于非参数的Census立体匹配算法。

本文根据Census 立体匹配算法的原理，分析算法存在的局限性；根据算法的局限性归纳算法的改进方向，并对各个改进算法对比；最后讨论Census算法的发展趋势。

1 Census 立体匹配算法描述

1.1 Census 立体匹配算法原理

Census 立体匹配算法的基本原理是建立以参考像素点为中心的窗口，以此窗口为滤波器，一一遍历匹配图像。 利用窗口内中心像素的灰度值和邻域像素的灰度值的大小关系将原本的邻域像素灰度值转化为二进制字符，整个滤波器使得邻域像素形成二进制字符串，比较两个字符串的汉明距离即为参考像素点与匹配像素点之间的匹配代价值。Census 立体匹配算法是在立体匹配的算法中引入了非参数变换的思想[12]。 Census 代价计算过程原理简单，不需要大量的计算，运行速度快[13]，同时Census 变换一定程度上抑制了噪声和光照不均匀造成的误差。 但是，由于立体匹配是一个“病态”问题，使得算法总存在一定的局限性。

1.2 Census 立体匹配算法局限性

根据Census 立体匹配算法的变换过程， 可将Census 立体匹配算法的局限性归纳：

1） Census 变换过程中先确立一个固定的窗口，这个固定的窗口在视差不连续区域会带来一些无用点，影响视差图的精度。

2） Census 在变换过程中是邻域像素灰度值和中心像素点的灰度值进行大小的比较，一旦中心像素点发生突变，会使得匹配结果产生极大的误差。

3） 在Census 变换过程中只利用了邻域像素的灰度信息，使得邻域像素的纹理、颜色、距离等信息大量丢失，造成误匹配。

4） 在Census 变换过程中只考虑中心像素和邻域像素的关系，忽视了邻域像素和邻域像素之间的关系，影响视差图精度。

In Figure 1: λ is the traveling wave wavelength, mm; 2a is the contact area length, mm; hm is the thickness of the friction material layer, mm; Wz is the vertical amplitude of the traveling wave, mm. The traveling wave equation of the stator surface can be written as follows

2 改进的Census 立体匹配算法

为了增强Census 立体匹配算法的性能，近年来提出了许多Census 立体匹配的改进方法。 以下将Census 的改进方法分类归纳。

2.1 基于变换窗口的Census 立体匹配算法改进

Census 代价计算中如何选择合适的窗口是一个难题[14]。窗口过大可能导致视差不连续，产生大量“无用点”， 窗口过小造成无法区分图像纹理信息，产生误匹配。传统的Census 立体匹配算法计算代价函数时，选定固定的窗口去寻找匹配像素点，当遇到视差不连续区域时，窗口内的像素灰度值变化较大，可能会造成误匹配。 基于可变窗口对传统Census 立体匹配算法优化，优化思路分为2 种：①改变窗口的形状，在视差不连续区域根据梯度算子[15]计算出边缘，从而确定窗口大小，使其保持在视差连续区域，去除了视差不连续区域的“无用点”；②通过对窗口内的像素点赋予权值，减少视差不连续区域的误差，从而降低“无用点”对代价值的影响。

匹配窗口不一定都是n*n 的正方形窗口，也可选择长宽不等的矩形窗口， 降低视差不连续区域“无用点”带来的误匹配。 张丽君[16]的实验结果发现采用长比宽短的形状在竖直边缘深度不连续区域可得到较高精度的视差图，采用长比宽长的形状在水平视差不连续区域可得到较高精度视差图。 雷磊等[17]采用高斯模板确定代价计算的窗口，把窗口内的像素坐标带入高斯函数中确定各个邻域像素点的权值，从而降低“无用点”带来的误差。黄超等[18]通过窗口内像素灰度的平均值调节窗口形状，设置最大窗口值和阈值来确定最佳的窗口，一定程度上也可以减少误匹配。

2.2 基于中心像素灰度值的Census 立体匹配算法改进

大多数Census 立体匹配算法的改进都是基于中心像素点的改进。在代价计算过程中Census 立体匹配算法过度依赖中心像素点的灰度值，使得Census 立体匹配算法产生的视差图精度较低。 为了防止中心像素点突变造成的误匹配，可从以下思路优化：以窗口内像素点灰度的平均值代替中心像素点的灰度值，理论上可以减少中心像素突变产生的误差；利用窗口内像素点之间的信息，判断中心像素点是否发生突变。

Ma[19]，Chang[20]，刘建国等[21]为改善中心像素点突变造成的误匹配，利用邻域像素平均值代替中心像素灰度值，此方法在一定程度上提高了初始代价值的可靠性。 理论上也可选择中心像素点邻近的四邻域或八邻域像素点的灰度值的平均值[22]来代替中心像素点的灰度值；刘爽等[23]将窗口内的灰度值进行排序，去除最大值和最小值之后求取均值，再进行比较，相比于用窗口内的所有像素平均值可靠性更高；黄彬等[24]利用正态分布为窗口内像素点的距离设置不同的权重即格式塔原理[25-26]，设定一个阈值判断中心像素点是否突变，这样大大降低了噪声对视差图的影响，使得初始视差图中的噪声点明显减少。

2.3 基于邻域像素其他信息的Census 立体匹配算法改进

邻域像素的灰度平均值虽然一定程度上可以降低误匹配，但未能充分利用各个邻域像素与参考像素之间的其他特征关系。 为了防止邻域信息的大量丢失可以利用窗口内邻域像素的距离、 颜色、纹理、梯度等信息对中心像素点的灰度值进行控制。

梁海波等[27]在Census 代价计算过程中加入了局部纹理反差加权项[28]描述图像的方向性，用邻域像素平均值和局部纹理反差项代替中心像素点灰度值， 此方法增加了二进制字符串的排列方法，减少了误匹配；侯华等[29]利用色补理论即两个像素的灰度值为窗口内的最大值和最小值，则这两个像素颜色互为补色，来改变中心像素灰度值，使得在代价计算过程中加入了邻域像素的颜色信息，同时在中心像素发生突变时也不会影响视差图的精度，提高了代价匹配的抗干扰性。 徐源等[30]将Census 立体匹配算法代价计算过程中的灰度值比较改成了中心像素点和邻域像素点之间的梯度比较，进而计算汉明距离，一定程度上减少了对中心像素点的过度依赖，时间复杂度相对较低，同时精度有所提高。

2.4 基于二进制字符串的Census 立体匹配算法改进

在不改变中心像素点灰度值的情况下，为了提高传统Census 立体匹配算法精度， 改进的Census立体匹配算法可从弱化中心像素点为唯一决定性角度出发，利用邻域像素之间的信息对中心像素点进行约束， 降低中心像素点发生突变时产生的误差。 改进的思路大致分为两类：在邻域像素灰度值和中心像素比较之后，再把邻域像素灰度值和像素平均值进行比较，或者邻域像素和邻域像素进行比较，增加编码长度，降低误匹配率；引入控制噪声的变量，使邻域像素灰度值与其比较，也可以增加编码长度，从而降低误匹配率。

2.5 基于代价聚合的Census 立体匹配算法改进

对于Census 立体匹配算法得到的视差图精度不足等问题，也可进一步利用其他信息即代价聚合方法对视差图进行优化， 得到精度较高的视差图。大致可以分为3 个方向进行代价聚合：充分利用邻域像素颜色、距离、插值等信息进行优化；使用滤波的方法增加视差不连续区域的精度，使图像边缘保持平滑； 利用跨尺度的方法提高图像的分辨率，提高匹配代价的精度。

Woodfill 等[34]通过相近像素具有相似的颜色对中心像素进行优化；杨淑云[35]在代价聚合阶段利用四路径插值的方法优化邻域像素灰度值， 从而提高代价值精度；Yoon 等[36]利用了双边滤波以及He 等[37]采用引导滤波的方法对图像边缘信息进行优化，提高了边缘像素的匹配代价值的精度；Zhang 等[4]将多尺度的优化方法加入到代价聚合中，利用人眼由远到近的观察方式将图像分成不同的分辨率，大大提高了信息的利用率。

2.6 基于融合算法的Census 立体匹配算法改进

根据Census 立体匹配算法计算代价函数所导致的视差图精度不足的问题， 许多研究者提出了Census 算法与其他局部立体匹配算法融合来计算代价函数。 其思想就是用其它局部算法来弥补Census 计算代价函数过程中的缺点，从而降低误匹配率，提高视差图精度。 可以和梯度算法融合降低视差不连续区域的误匹配；和灰度差融合降低重复纹理区域的误匹配；和权重或者改进的灰度、梯度进行融合。

Mei[38]提出了一种很经典的AD（灰度差绝对值）和Census 的融合算法，实验结果表明，这两种算法的融合大大提高了在弱纹理和重复纹理区域的视差精度；萧红等[39]将传统的Census 算法和梯度算法融合， 相比于传统的Census 算法误匹配率大大降低；邹进贵等[40]将自适应权重的SAD 算法和Census融合，实验结果表明融合的Census 算法在时间复杂度不增加的情况下误匹配率大大降低，同时对亮度差异也有一定的抗干扰性，3 种算法的匹配代价融合也可以提高算法的精度。

3 改进Census 立体匹配算法对比分析

3.1 立体匹配算法优缺点对比分析

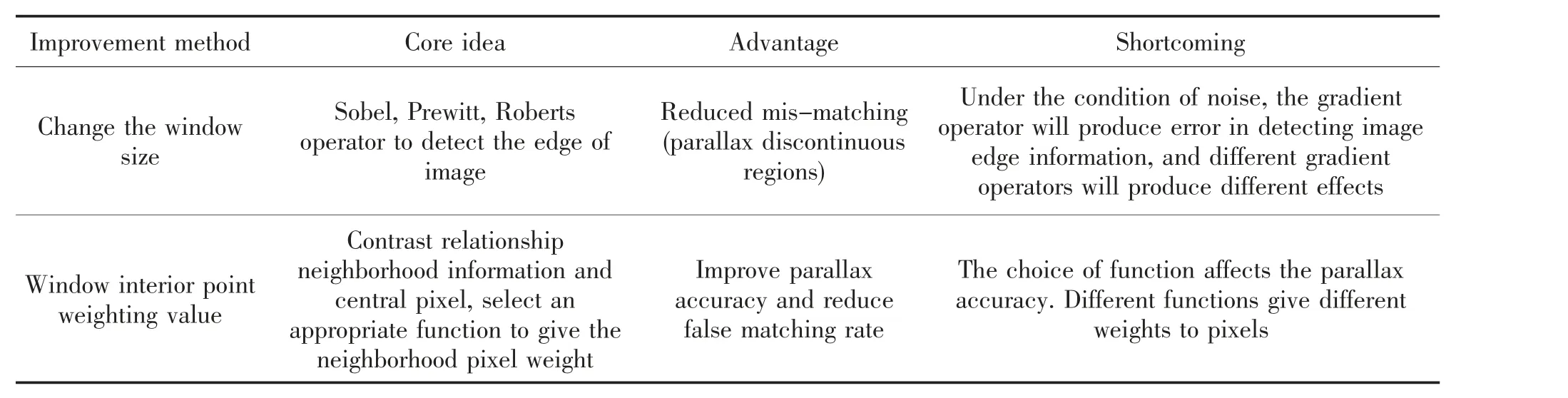
表1 基于变换窗口的Census 改进算法对比Tab.1 Comparison of Census improved algorithms based on transform window

表2 基于邻域像素平均化中心像素点Census 的改进算法对比Tab.2 Comparison of improved algorithm based on neighborhood pixel averaging center pixel census

表3 基于邻域像素其他信息Census 的改进算法对比Tab.3 Comparison of improved Census algorithm based on other information of neighborhood pixels

表4 基于弱化中心像素点为唯一决定性因素Census 的改进算法对比Tab.4 Comparison of improved Census algorithm based on weakening center pixel as the only decisive factor

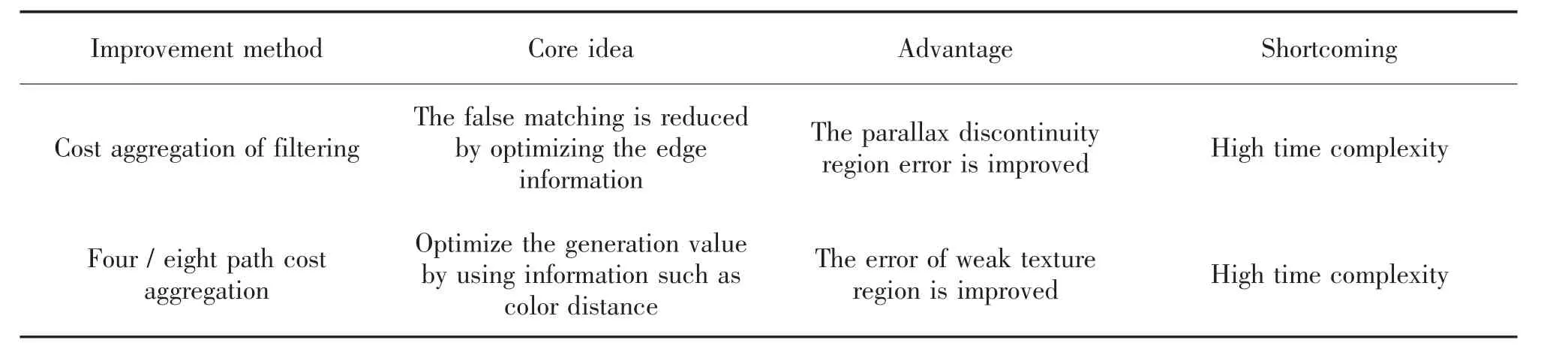
表5 基于代价聚合的Census 改进算法对比Tab.5 Comparison of improved Census algorithm based on cost aggregation

表6 基于融合算法的Census 改进算法对比Tab.6 Comparison of improved Census algorithm based on fusion algorithm

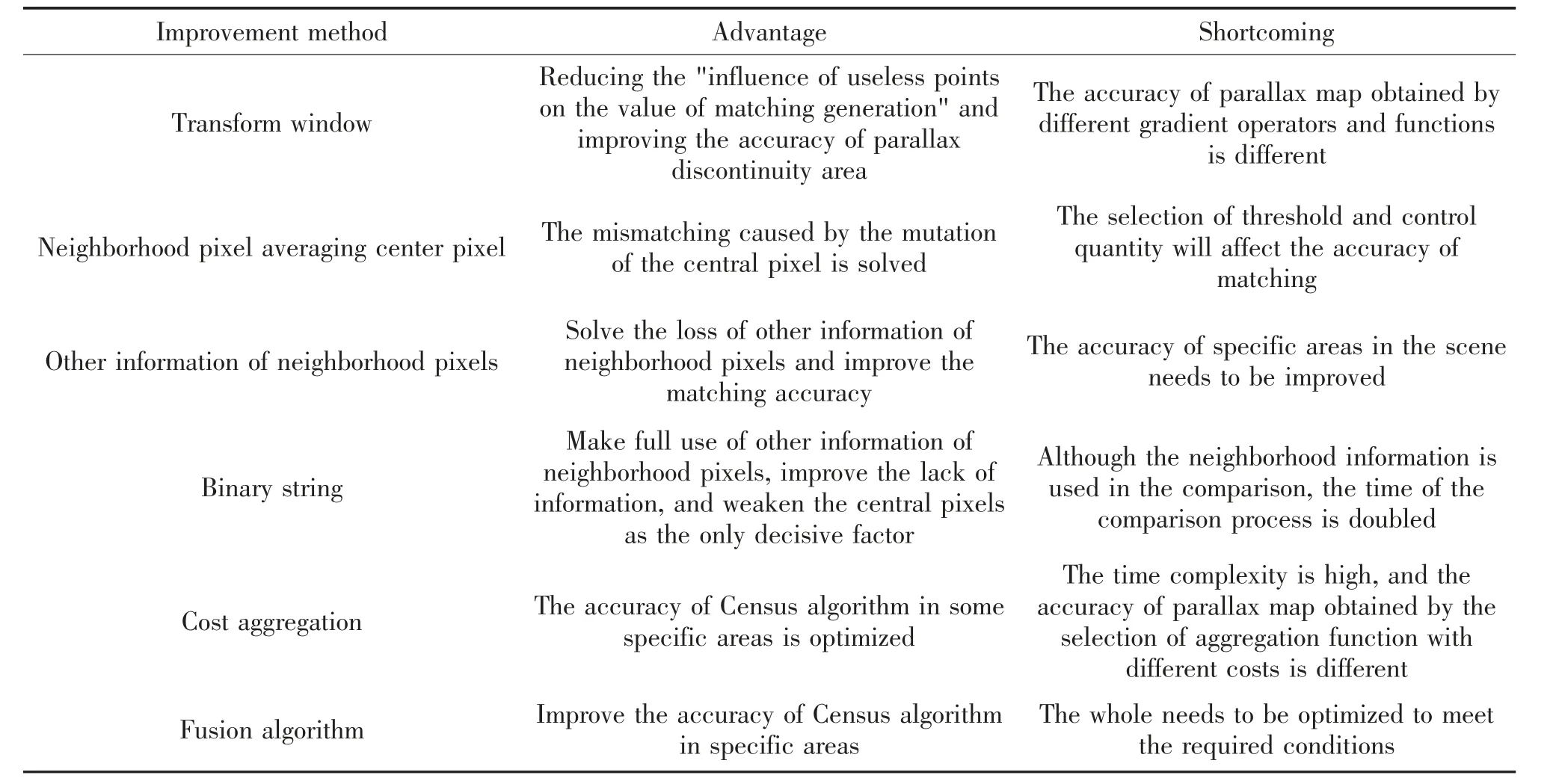
表7 各类改进Census 算法对比Tab.7 Comparison of various improved Census algorithms

3.2 立体匹配算法效果图对比分析

算法是在Visual Studio 2019 软件平台上使用C++操作实现的， 采用集数据集Middlebury 上的Cones 图像对算法进行验证[41]，实验环境为Windows10，X64 系统，Intel Core i5-7200U，主频为2.50 GHz。部分改进后的Census 立体匹配算法效果图如图1 所示。

图1 Census 算法效果图Fig.1 Effect of census algorithm

改进的算法一定程度上提高了视差图的精度，不同的改进算法在弱纹理，重复纹理等区域都有一定程度的视差精度的改善。 但在视差不连续区域的匹配精度效果仍然不太理想， 有待改进。 以上改进的Census 立体匹配算法中还存在大量的噪声点，因此在实际应用中往往根据Scharstein D[42]的视差计算步骤对改进后的视差图进行视差优化以达到需要精度。

改进算法匹配代价时间对比如表8 所示。

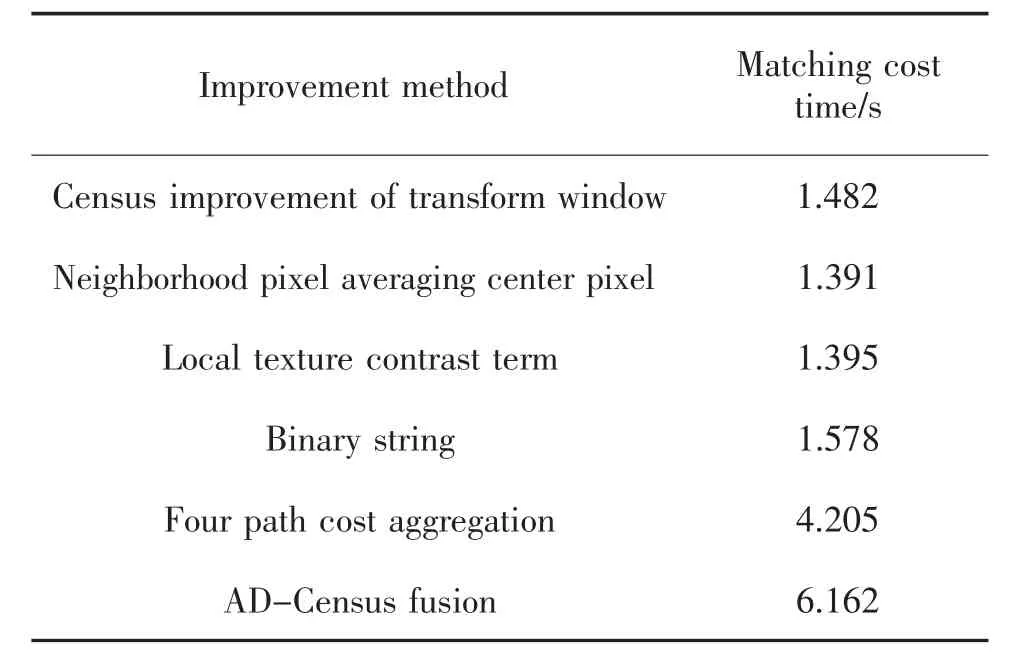
表8 改进Census 算法效果图的时间对比Tab.8 Time comparison of the improved Census algorithm effect diagram

改进算法效果图精度越高相对的时间复杂度越高。

4 Census 立体匹配算法的应用和发展趋势

双目匹配是计算机视觉中一直以来存在的问题之一，双目匹配是一个“病态”问题，已有近40 年的实践和研究。 多年来，立体匹配算法从全局算法到局部算法以及像素级的各种转变为连续优化和离散优化。因为Census 局部立体匹配算法相对来说原理简单、运行速度快、匹配精度较高和抗干扰性强，使得Census 算法在重建实时交互性三维场景得到广泛应用，是获取三维场景结构信息的研究热点之一；在FPGA 上最常用的就是Census 算法[43]，它结构简单，易于并行化，生成的视差图精度高并且在满足实时性的要求下可提高特定区域的匹配精度[44]；对于弱纹理场景和光照不一致场景也能得到较为精确的视差图；同时基于Census 立体匹配算法可用于医学上外科手术导航、无人车驾驶的路线规划及目标勘测，都可快速地找到立体相对的匹配[45]。 但是Census 立体匹配算法也存在一定的局限性，因此改进的Census 立体匹配算法可以使得寻找的立体匹配像对的精度更高。

立体匹配算法的实施要考虑诸多因素，并要以计算的稳定性和复杂度等总体性指标来衡量算法的有效性和可行性。因此对于研究Census 立体匹配算法应从系统的角度来分析，未来的发展趋势也要在以下几方面有所侧重：

1） Census 立体匹配算法和其它方法的有效融合。 由于立体匹配是一个“病态”问题，每一种算法在不同的场景都有各自的优缺点。 Census 立体匹配算法是基于局部特征进行的立体匹配，缺乏全局信息，因此可将Census 立体匹配算法融合到全局立体匹配算法框架中进行整体改进。

2） 提高Census 立体匹配算法在特征缺乏、纹理重复、遮挡和不连续区域的视差图精度。 由于场景中存在噪声、纹理重复、无纹理以及视差不连续等不可抗的因素， 导致匹配过程中容易产生误差。得到特定区域的高精度视差图是Census 立体匹配算法未来的发展趋势。

3） 建立实时的、稳定的、实用的Census 立体匹配算法[46]。在提高算法的匹配精度的同时，时间复杂度也是必须要考虑的一个因素。 目前大多数算法都是基于精度的提高对Census 算法进行的改进，因此在确保精度的条件下，减少Census 立体匹配算法代价计算过程中的时间复杂度是未来的发展趋势，使得Census 立体匹配算法在实时计算中得到广泛的应用。

4） Census 立体匹配算法和深度学习算法结合。人工智能算法越来越多的应用于解决立体匹配问题。 最近机器学习的兴起和深度学习的迅速普及增强了立体匹配新的发展趋势和应用，这在几年前是不可想象的。 有趣的是，这两个世界之间的关系是双向的。 机器学习，尤其是深度学习，推动了立体匹配技术的发展，而立体匹配技术本身又开创了新的方法。 它们提供了各类求解复杂系统优化问题的通用框架，可以此为基础建立智能化Census 立体匹配算法。

5 结束语

Census 立体匹配算法相对来说匹配精度较高，抗干扰性较强，但是还是具有一定的缺陷。 本文主要综述了Census 立体匹配算法的缺陷， 归纳了Census 立体匹配算法的改进方向以及对各个改进的算法进行了对比，分析了它们的优缺点、各个改进算法的效果图以及时间复杂度。 虽然立体匹配算法的研究已经经过了很多年，但是Census 立体匹配算法无论是在理论上还是实际应用方面都有一定的局限性。对于Census 立体匹配算法未来主要考虑它的精度和时间复杂度的进一步优化。 在提高算法匹配精度的同时，时间复杂度也是必须要考虑的一个因素。