基于FLAC3D的桩板结构在堆积体边坡中的地震响应评价

曲宏略，张 哲，李兆龙，陈 爽，王希科，马耀先

(1.西南石油大学 地球科学与技术学院，四川 成都 610500； 2.天然气地质四川省重点实验室，四川 成都 610500； 3.中铁二十三局集团第一工程有限公司，山东 日照 276826； 4.云南建设基础设施投资股份有限公司，云南 昆明 650501； 5.天津市水务规划勘测设计有限公司，天津 300204； 6.四川盛唐建设工程有限公司，四川 成都 610042)

堆积体主要是由滑坡堆积、残坡堆积、崩坡堆积、冲洪堆积等第四系堆积作用形成的地质体，属于斜坡变形破坏后继续运动阶段的产物[1]，堆积体边坡在我国西南山区广泛分布。汶川震害调查表明，崩塌滑坡类灾害中堆积体滑坡占了较高比例[2-3]，桩板结构作为当前治理边坡地质灾害的主要措施，已被广泛地运用于各类工程建设中。近年来，关于桩板结构动力响应特性国内外学者做了很多研究[4-5]，大致可以分为两大类：一类是通过大型振动台试验[6]，对桩板结构地震响应相关物理量(如：加速度、位移、土压力等)直接进行监测，并进行分析[5，7-8]；另一类是以数值模拟为基础，通过数值分析软件(如：FLAC、ABAQUS等)，进行桩板结构的数值仿真分析[9-11]。尽管关于桩板结构的动力响应已有不少研究，但通过调研分析可以发现，大多数学者以具体工程为基础，针对某一工点进行分析，或者针对影响桩板墙加固效果的个别参数进行探讨，缺少综合考虑多种参数的研究。因此，本文以数值模拟为基础，借助FLAC3D仿真计算软件，结合实际工点的边坡参数，进行多参数的桩板墙动力响应特性分析，对比不同参数对桩板墙加固效果的影响，为工程设计提供参考。

1 数值分析模型

根据前期勘察资料，川藏线路实际工程边坡设计断面图如图1所示，从机理分析的角度出发，结合此实际工程边坡，本文建立的计算模型如图2所示，其中X方向(顺坡向)总长110 m，Y方向(坡宽)20 m，Z方向(坡高)56 m，坡度约40°，此次研究为堆积体边坡模型，滑坡体为松散堆积体，滑床为基岩，滑床基岩各处岩性一致，产状相同。

模拟桩板墙桩身采用C30钢筋混凝土灌筑，截面尺寸为2.0 m×2.0 m，桩长12.0 m，桩间距为4.0 m，模拟桩间挡土板采用C30钢筋混凝土制作。桩、挡土板采用线弹性模型，土体采用Mohr-Coulomb弹塑性模型，对于桩土界面采用无厚度接触面单元“interface”单元进行模拟[12]。模型所需要的参数有：剪切模量G、体积模量K、黏聚力c、摩擦角φ、以及密度ρ。其中c、φ、ρ的取值由实测得出，G、K由公式换算得出[13-14]，G和K的计算公式如下：

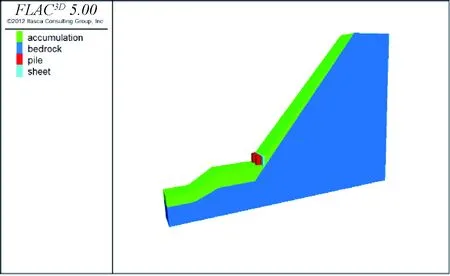
图2 堆积体边坡计算模型Fig.2 Calculation model of deposit slope

(1)

(2)

其中，E为弹性模量，μ为泊松比。

滑床、滑体参数取值由现场实测得到，桩、挡板根据工程地质条件和相关规范选定参数，模拟实际工况进行研究，如表1所示：

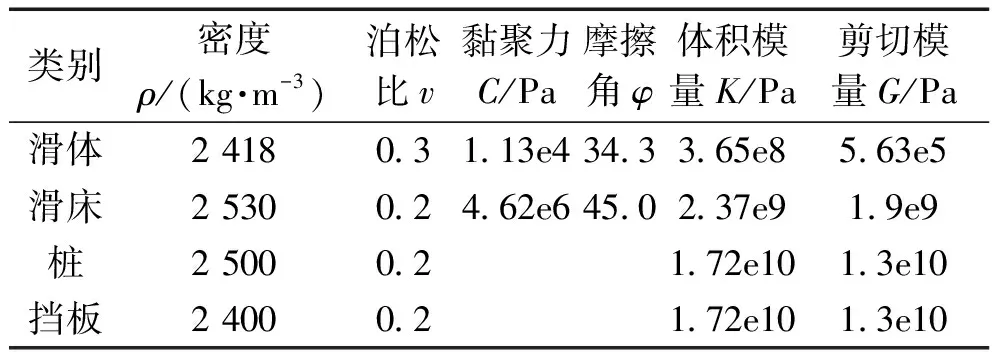
表1 模型计算参数表

静力计算时，模型底部固定，模型两侧施加Y方向约束，模型前、后方施加X方向约束。动力计算时，模型四周采用自由场边界[15]，在模型底部分别输入EI-Centro波、汶川波、Kobe波水平向(X向)和竖直向(Z向)双向加速度时程作为地震激励，加速度峰值强度为0.957 g，为节约计算时间，地震动加载时间取为30 s，这段时间包括了地震加速度时程中的较大振幅部分[16]。参考已有模型分析实例[17]，局部阻尼系数不用求解系统的自振频率，而且相对于瑞丽阻尼而言不会减小时间步，较适合于简单问题的求解，因此模型采用局部阻尼，阻尼系数取为0.157来近似表征土体在地震波传播过程中的阻尼作用。

2 桩板墙动力响应特征分析

桩板墙中挡土板主要起挡土作用，主要承力结构为抗滑桩，分析抗滑桩受力，最重要两点就是土压力和位移[18-19]，因此，本文先分析土压力、位移的特点，再更改不同参数，对不同参数下桩板墙的抗震效果进行探讨。

2.1 土压力

桩板墙在抗震设计过程中，其截面设计、配筋计算都受桩身所受剪力和弯矩的严重影响，而土压力正是产生桩身剪力、弯矩的原因，因此，数值计算对土压力沿桩身的分布情况加以分析。通过分析计算，得到土压力沿桩身分布曲线见图3。由于此次设计桩长12 m，故距桩顶距离-6 m以上为地上悬臂段，-6 m以下为地下嵌固段。

图3 土压力沿桩身分布曲线Fig.3 Soil pressure curve along pile

由图3可知，在地面以上悬臂段，桩身土压力较嵌固段小得多，在地面处，桩身土压力突变增大，且由悬臂段正值变为负值，增大幅值达到900 kPa，说明此处桩身承受土压力最大，也是抗滑桩最易产生破坏位置，在工程设计时，应重视地面位置(悬臂段与嵌固段结合位置)桩身的强度。

2.2 位移

为研究桩板墙在地震作用下的桩身变位反应，对模型进行X方向位移监测，并进行分析计算，得到桩板墙桩身位移沿桩高的分布曲线，如图4所示。

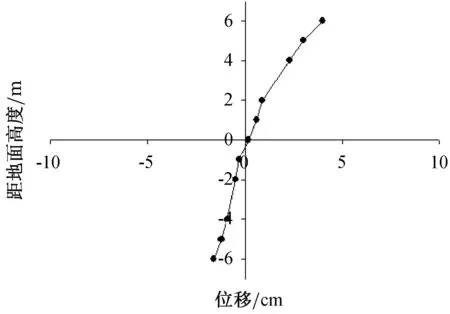
注：数值为“+”代表向自由面方向位移，“-”值代表向坡体内部位移。图4 位移沿桩身分布曲线Fig.4 Displacement curve along pile

由图4可以看出，抗滑桩悬臂段位移为正值，且桩顶位移最大，随着高程降低位移逐渐减小，而嵌固段位移为负值，桩底位移最大，且随着高程增加位移逐渐减小，这说明地面以上，桩身承受土压力向桩外，而地面以下桩身承受土压力向坡内，进而表明抗滑桩产生了一定的向自由面方向的“倾覆”。对比悬臂段和嵌固段整体位移，可以发现，地面以下明显比地面以上位移小，这表明受土体限位影响，嵌固段位移较小。但结合土压力分析，可知地面以下土压力较大，说明悬臂段抗滑桩由于较大位移，释放了一定土压力，进一步可以推测，抗滑桩破坏主要为地面处的折断或整体“倾倒”破坏。

3 桩板墙不同参数影响分析

为分析不同参数对桩板墙抗震效果的影响，更改模型计算的不同参数，通过改变地震波、峰值地面加速度(Peak Ground Acceleration, PGA)、桩间距、桩体嵌固深度以及不同土体参数(c、φ)分析桩板墙的抗震效果。

3.1 不同地震波影响分析

对堆积体边坡模型分别加载EI Centro、Kobe和汶川卧龙三种地震波，PGA归一化为0.1 g，分析不同地震波下的桩身土压力和位移，如图5—图6所示。通过FLAC3D进行自振频率计算，自振周期约为0.362 s，自振中心频率为2.76 Hz。在自振周期0.362 s附近，加速度反应谱幅值排序为汶川卧龙>El Centro>Kobe。

从图5可以看出，不同地震波作用下，桩身土压力有所不同，但差距不大，土压力表现出汶川卧龙>EI Centro>Kobe,对照结构自振频率和地震波频率，可以得出，结构自振频率和地震波频率对结构抗震效果影响较大，在结构自振频率附近地震波幅值越大，则对结构抗震越不利。

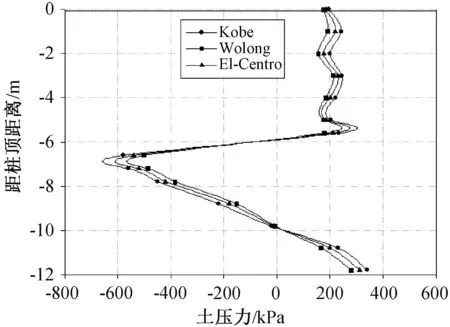
图5 不同地震波作用下土压力Fig.5 Soil pressure of different seismic waves

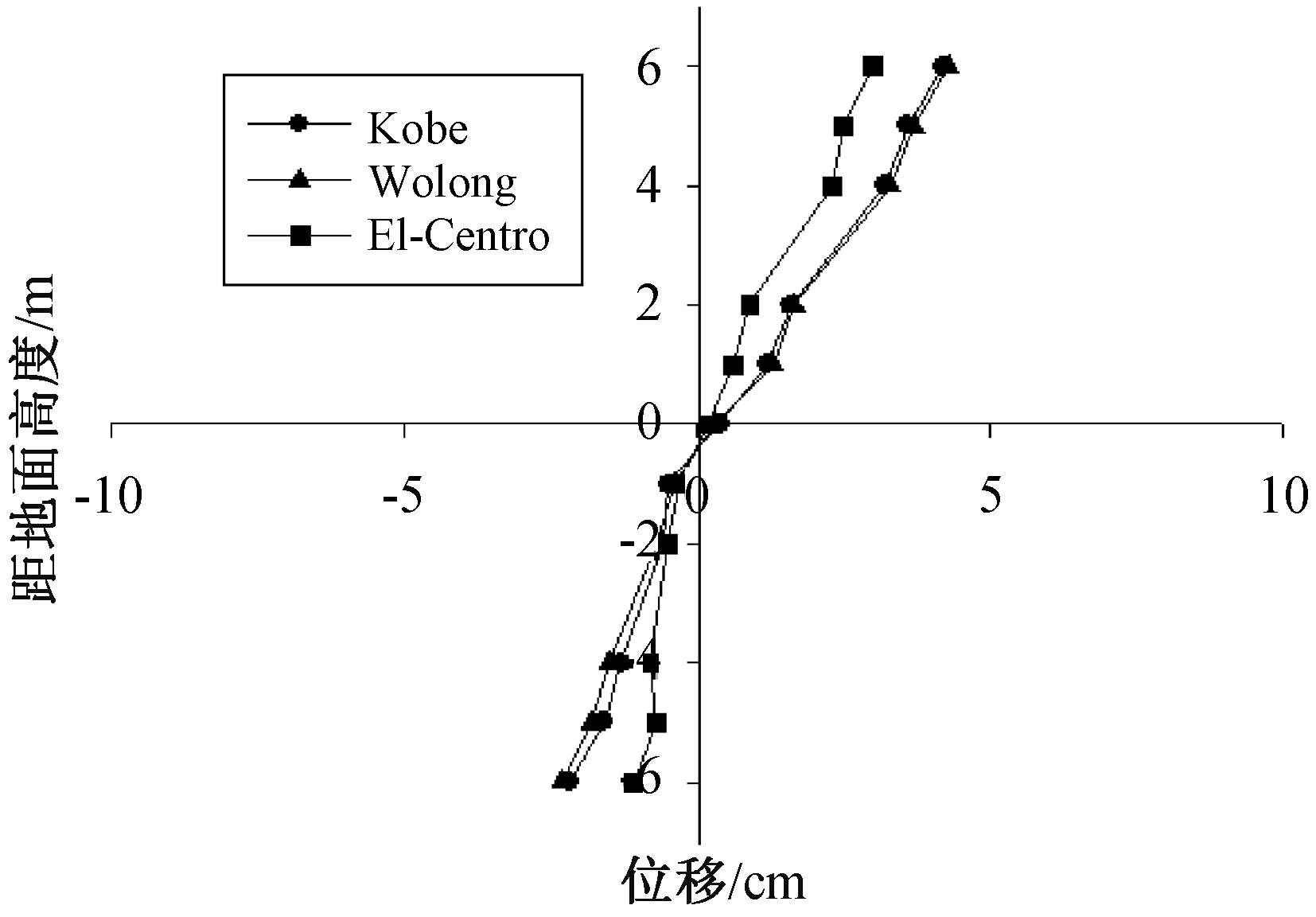
图6 不同地震波作用下桩身位移Fig.6 Pile displacement of different seismic waves

从图6可以看出，在不同地震波激励下，桩身位移同样表现出汶川卧龙>El Centro>Kobe，即位移的响应情况与结构自振周期附近加速度反应谱幅值排序的结果一致。结合土压力分析，充分说明汶川卧龙波对边坡破坏作用最大，Kobe波最小，进一步可以得出，针对不同地区，不同边坡的抗震设计，应考虑坡体自振频率与地区地震特征。

3.2 不同PGA影响分析

选取EI地震波，对堆积体边坡模型，分别加载PGA为0.1、0.2、0.4 g的地震加速度，以模拟结构在地震基本烈度VII度、VIII度和IX度区域的响应情况，对比分析计算结果如图7、图8所示。

由图7可以发现，当PGA较小时(0.1、0.2 g)，桩身土压力增长不明显，但当PGA达到0.4 g时，桩身土压力发生突变，急剧增大。说明，当地震烈度比较大时(IX度区以上)，抗滑桩需大幅提升强度。

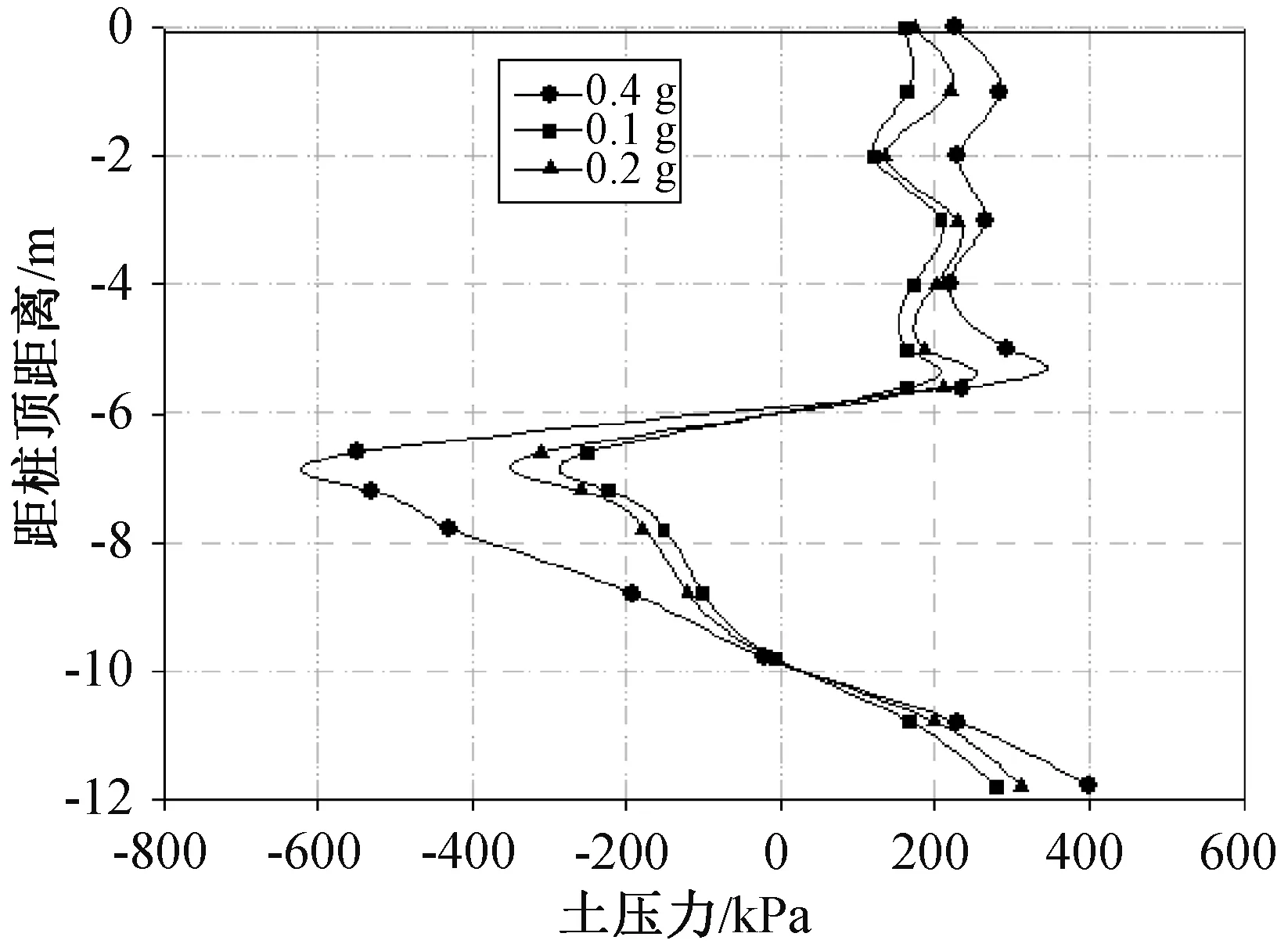
图7 不同PGA作用下土压力Fig.7 Soil pressure of different PGAs

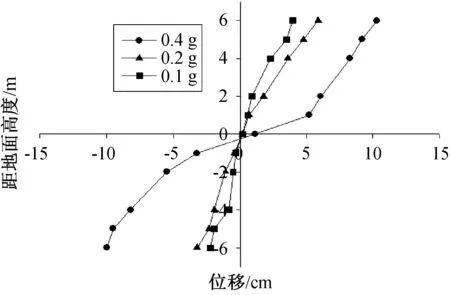
图8 不同PGA作用下桩身位移Fig.8 Pile displacement of different PGAs

从图8可以看出，随着PGA的增大，桩身位移不断增大，但在0.2 g时，桩身位移增长不大，说明此时抗滑桩仍能保持很好的抗震作用，对土体位移产生充分限位作用。但当PGA达到0.4 g时，桩身位移发生突变。位移达到10.5 cm，超过桩身长度的1%，此时抗滑桩已失去抗震作用。

3.3 桩间距影响分析

在原模型的基础上，调整桩板结构的桩间距，将原来的桩间距4 m加大为6 m、8 m。分别计算分析桩背土压力的变化，如图9所示。

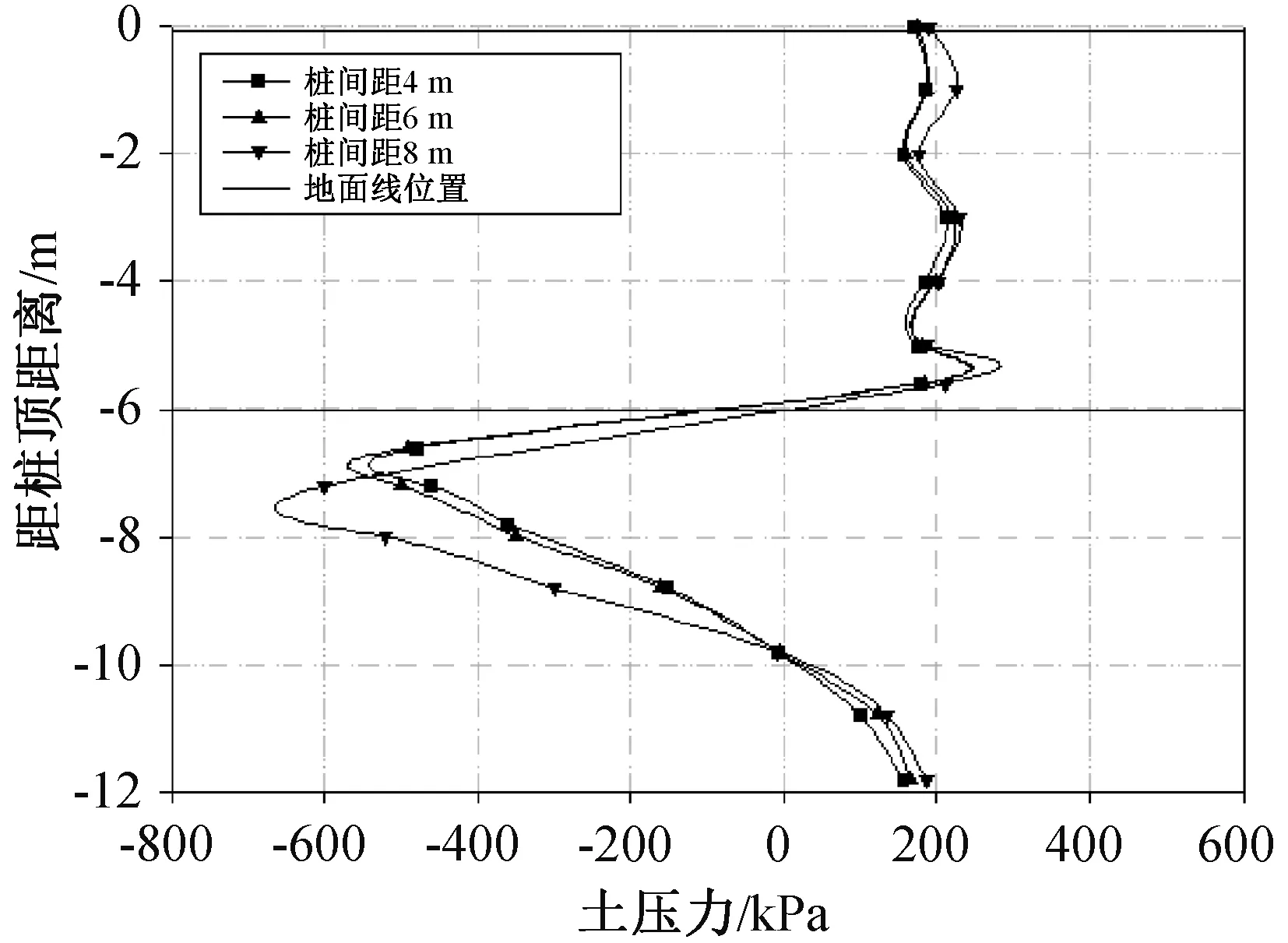
图9 不同桩间距土压力Fig.9 Soil pressure of different pile spacing

从图9可以看出，桩间距6 m时桩背土压力较4 m时稍大，但二者差距不大。当桩间距达到8 m时，土压力较二者有明显增大，主要表现为在抗滑桩嵌固段土压力显著提升。这是由于滑坡下滑力主要由抗滑桩承担，而桩间距的变化将直接导致抗滑桩对边坡的作用力重分布，当桩间距达到8 m时，已经超过桩长1/2。因此可以推测，当桩间距在一定范围内，桩背土压力变化较小，但超过这一范围，土压力增幅或减小明显，在进行桩板墙设计时，桩间距不应超过桩长的1/2。

3.4 嵌固深度的影响分析

抗滑桩的嵌固深度与嵌固地层的强度、所受推力、桩身刚度等条件有关。为研究嵌固深度对桩板结构的抗震影响，在原模型的基础上，分别减小嵌固深度至3 m(桩长1/3)和增大嵌固深度至9 m(接近桩长2/3)，对比原嵌固深度6 m(桩长1/2)，土压力沿桩身分布见图10，桩身位移对比见图11。

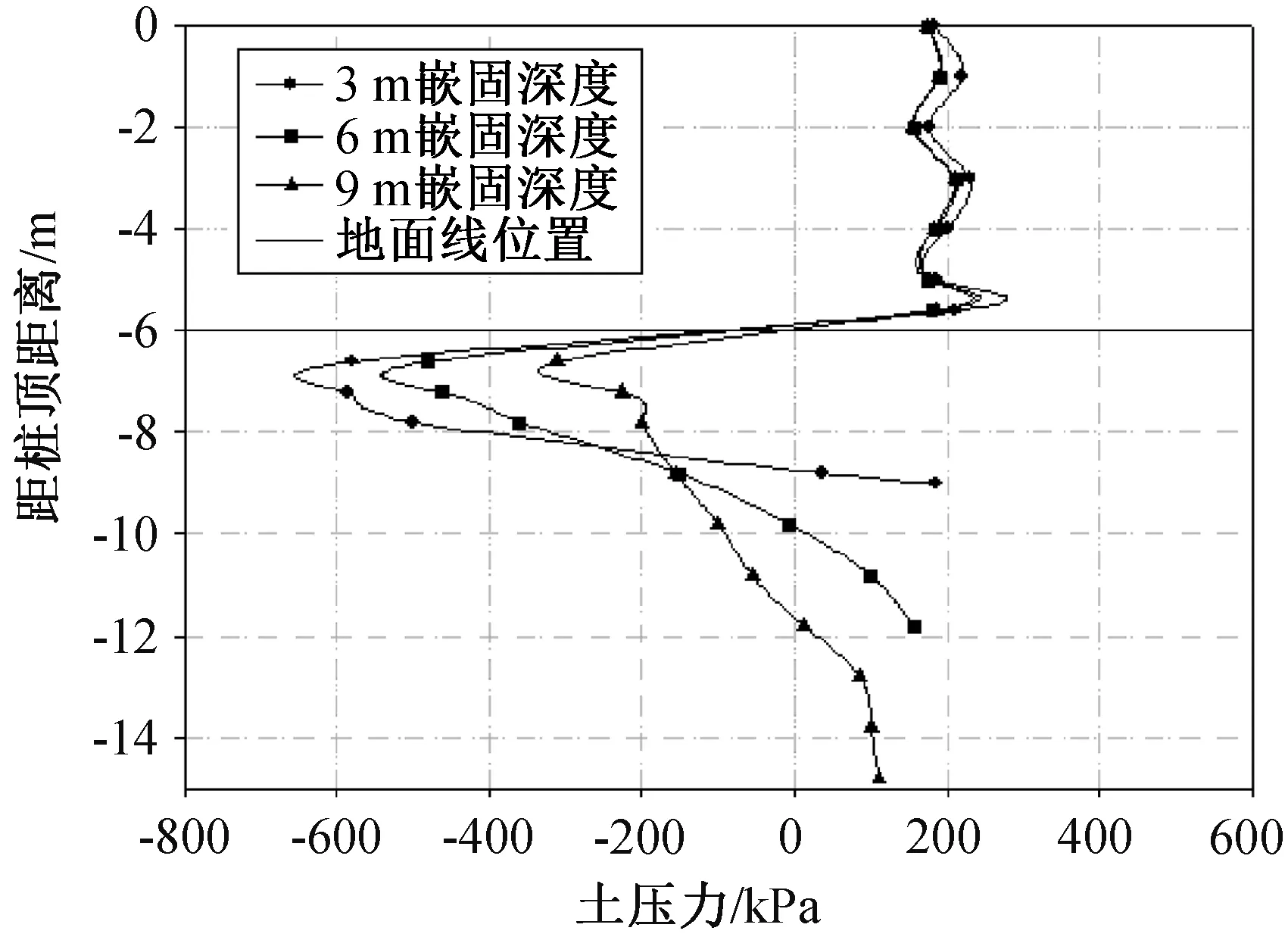
图10 不同嵌固深度土压力Fig.10 Soil pressure of different embedded depth

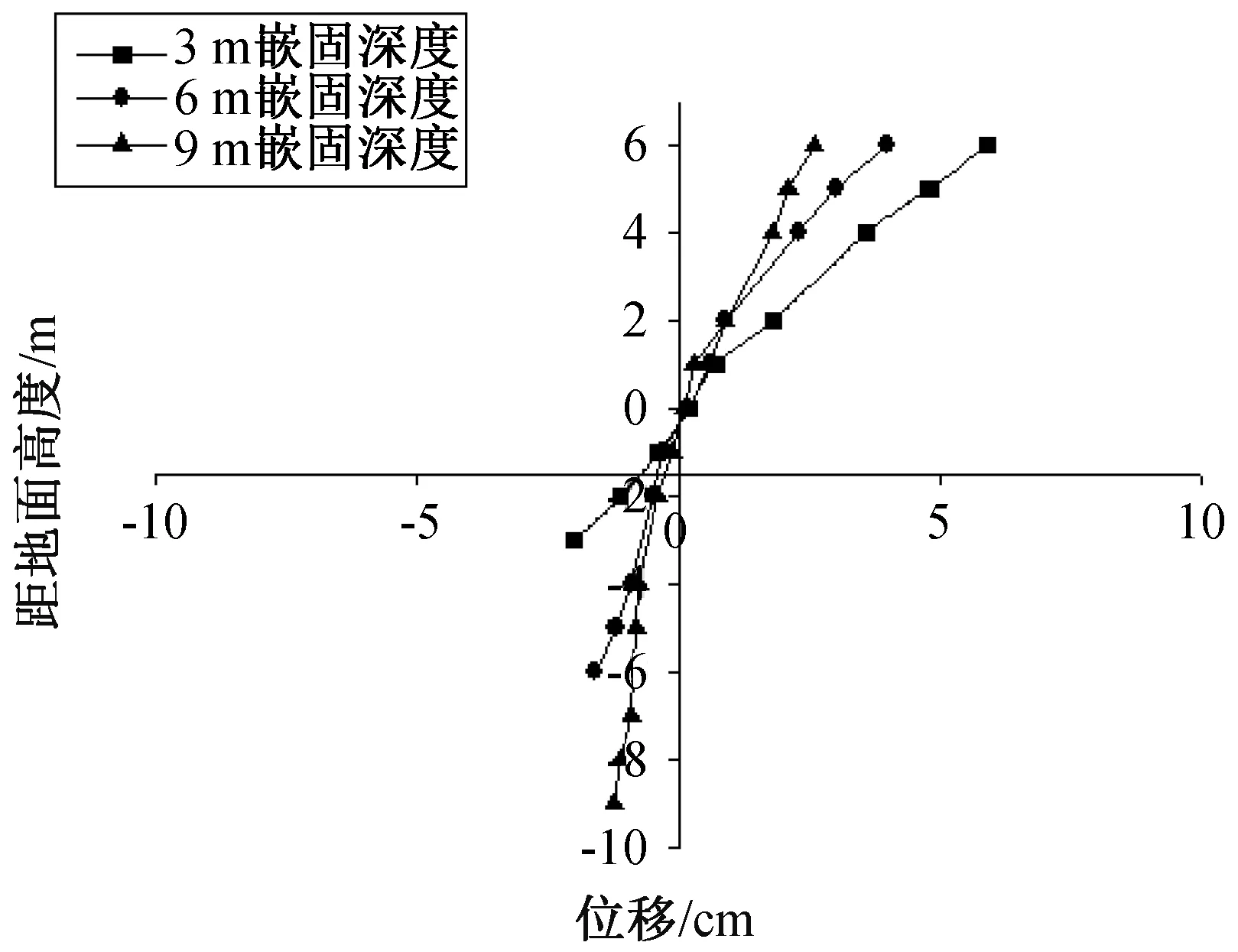
图11 不同嵌固深度桩身位移Fig.11 Pile displacement of different embedded depth

由图10可见，对于悬臂段，桩背所受滑坡推力分布对改变嵌固段长度的反应不大，说明滑坡推力主要受地震烈度、滑动面土体参数、滑体容重等自身参数控制，改变嵌固深度对于改善悬臂段桩身受力分布的效果不明显。而对于嵌固段，3 m嵌固深度的土压力明显大于6 m，说明嵌固深度的变浅直接导致了土体抗力的增加和土压力转点深度的变深，即结构需要在更短的嵌固段内产生更大的土体抗力，从而与滑坡推力在嵌固处产生的剪力和弯矩平衡；对比9 m嵌固深度，嵌固段桩背土压力要小的多，且桩身受力更均匀。所以，在工程设计中，建议抗滑桩嵌固深度最好达到桩长2/3，不能小于桩长1/3。

从图11可以看出，6 m嵌固深度桩顶位移为4 cm，3 m嵌固深度桩顶位移为5.9 cm，9 m嵌固深度桩顶位移为2.6 cm，嵌固深度3 m的变化，导致桩顶位移最多增加1.9 cm，增加较大，而桩身嵌固段位移最大增加1.1 cm，说明，桩身变位对嵌固深度的敏感度较高。在实际工程中，为减小桩身位移，可适当提升嵌固深度。

3.5 滑体黏聚力c的影响分析

岩土体材料自身属性，主要影响滑坡推力，调整滑体典型材料参数中的c为25、50和75 kPa，分别计算各自工况下的桩身受力、变位的地震响应情况，如图12—图13所示。

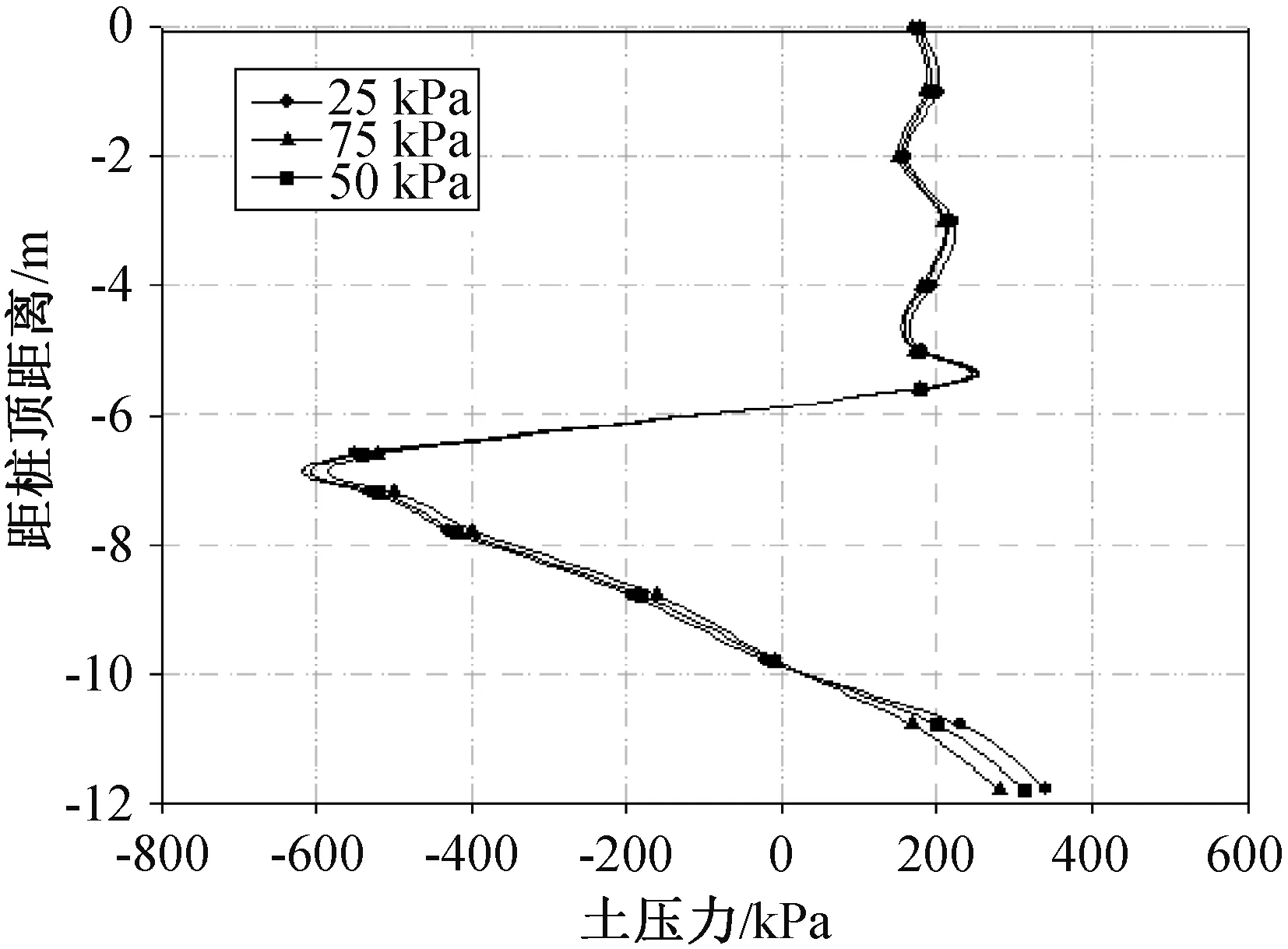
图12 不同黏聚力的土压力Fig.12 Soil pressure of different cohesion

从图12可以看出，不同黏聚力下，桩背土压力大致表现出25 kPa>50 kPa>75 kPa，但差距不明显。而根据图13，桩身位移虽同样表现出25 kPa>50 kPa>75 kPa，但差距较大。表明土体黏聚力的变化，对桩背土压力影响不大，但对桩身位移影响较大，在工程设计时，应着重考虑c的变化对桩身位移的影响。

3.6 滑体内摩擦角φ的影响分析

为分析内摩擦角φ对抗滑桩受力的影响，调整滑体材料参数中的内摩擦角φ为15°、20°和25°，分别计算各自工况下的桩身受力、变位的地震响应情况，见图14—图15。

图13 不同黏聚力的桩身位移Fig.13 Pile displacement of different cohesion

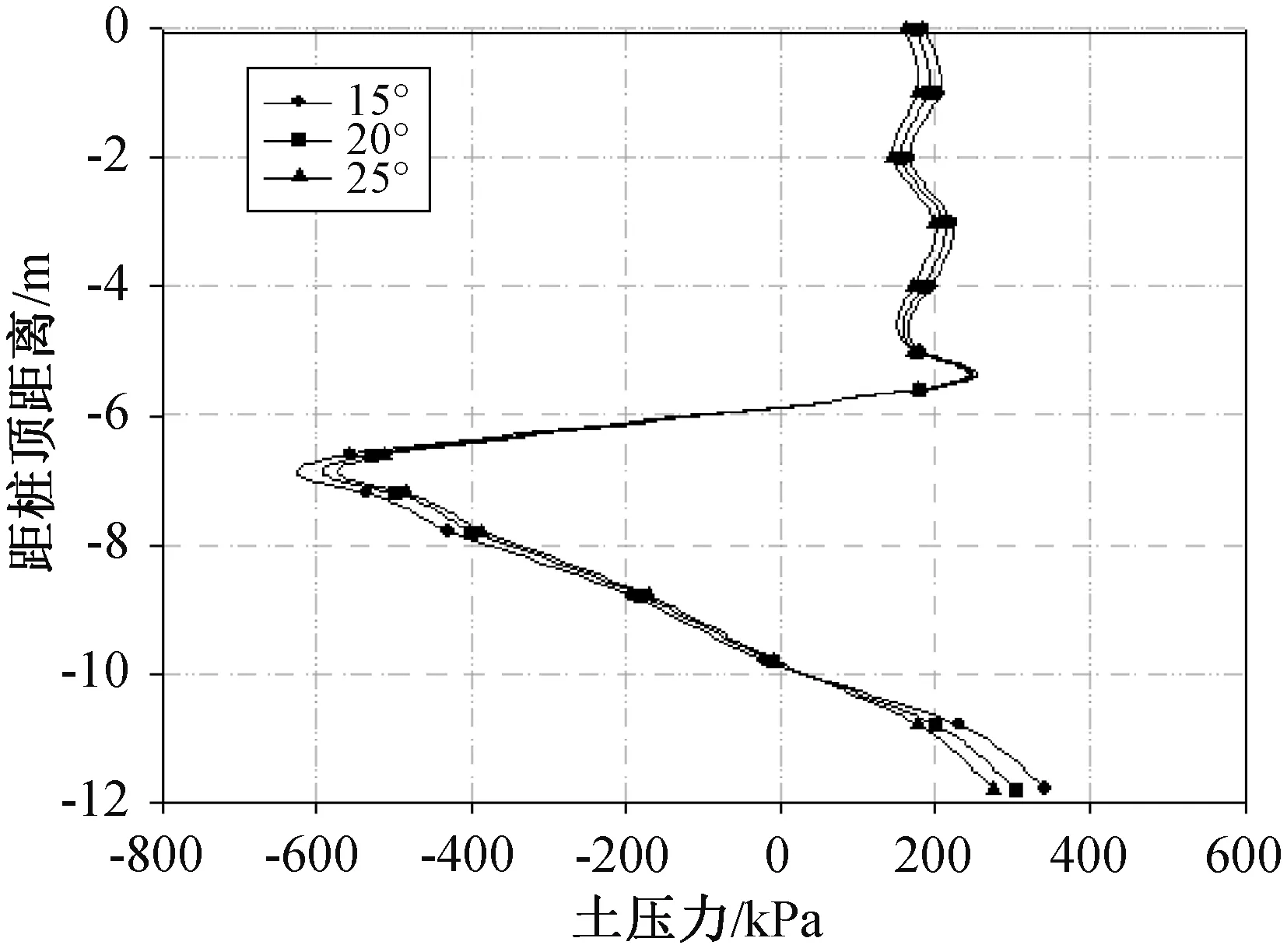
图14 不同内摩擦角的土压力Fig.14 Soil pressure of different internal friction angle

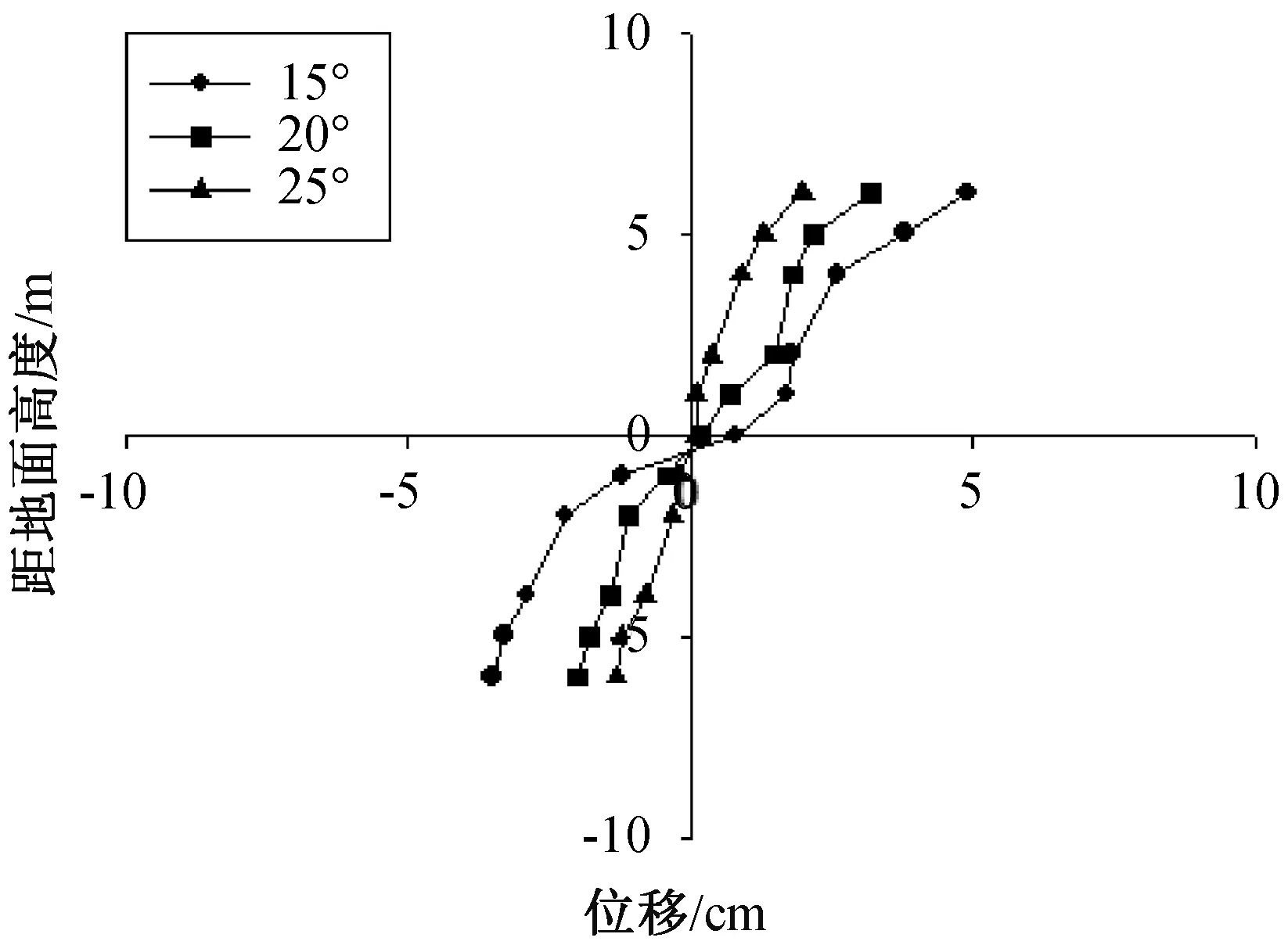
图15 不同内摩擦角的桩身位移Fig.15 Pile displacement of different internal friction angle

从图14、图15可以看出，随着内摩擦角φ的增大，桩身土压力和桩身位移均有所减小，其中，位移减小幅度更大，结合滑体黏聚力c的分析，可以得到，滑体自身参数对抗滑桩的抗震效果有一定影响，影响最大的为桩身位移。

4 结论

本文通过数值模拟软件FLAC3D，根据实际工况建立边坡模型，并进行了不同参数影响下的桩板墙动力响应特性分析，可以看出，桩身位移、土压力以及剪应力的响应情况与加速度反应谱幅值排序的结果一致，充分说明了结构抗震设计时动力特性对抗震效果的影响，另外，通过改变结构自身与外界条件的不同参数，主要得到以下结论：

1)在地震基本烈度VII、VIII度区，桩板墙可有效起到抗震作用，但在地震基本烈度IX度区，桩板墙桩身土压力较大，桩身位移超过桩身10%，不能满足抗滑需要。

2)桩间距的不同，直接导致了桩背土压力的分布不同，即滑坡推力和土体抗力会随着桩间距的减小而减小，但在一定范围内，减小幅度较小。

3)嵌固深度对悬臂段桩身的受力分布影响不大，而对于嵌固段的影响较大。随着嵌固深度的增加，土体抗力逐渐较小，即当嵌固深度较小时，结构需要产生更大的土体抗力与滑坡推力在嵌固处产生的剪力和弯矩平衡。

4)滑体参数选择直接影响着滑坡推力的计算和整治工程方案的选定。随着黏聚力c值和内摩擦角φ值的增大，桩板结构在地震作用下的位移减小，桩身受力减小。