一种改进的LiDAR点云滤波方法

马小陆，甄文雪，巩朝光

(安徽工业大学 电气与信息工程学院，安徽 马鞍山 243000)

激光雷达(LiDAR)因其测距精度高、实时扫描速度快、稳定性等特点，现被广泛应用在机器人等领域中，激光雷达获取的点云信息反映的是其与周围物体之间的距离信息。因此对原始点云数据的处理非常重要，它是获取高精度点云数据信息的基础[1]。

点云数据噪声表现为物体表面(包含物体边缘)一些随机分布的点，为了平滑这些噪声点，当前对原始点云数据的处理主要采用滤波方法，如万剑华等[2-3]提出基于曲面进行二次约束的方法，该方法能够对物体表面点云进行滤波；隋立春等[4-5]提出一种提取形态学点云滤波的处理方法；以双边滤波思想为核心，郑丽娟等[6-8]提出新的噪声检测过滤方法，该方法能够有效滤除数据和图像中的噪声；杨宏飞等[9]提出基于加权因子的双边滤波方法，该方法能够滤除离散波动较小的噪声；除此之外，Alexa等[10]提出基于多项式局部逼进曲面移动最小二乘(Moving Least-Squares，MLS)算法，得到较平滑的物体表面；Chen等[11]提出隐藏式移动最小二乘方法(Improved Moving Least-Squares，IMLS)，构建了接近隐式曲面；Zhang等[12]提出加权最小二乘方法加快了MLS，这些方法具有速度快的优点，但都对噪声敏感，稳定性差。戴士杰等[13]提出的张量投票算法和朱广堂等[14]提出直接使用曲率结合阈值的方法对特征点进行滤波会导致准确度下降。

综上可以看出，当前的点云滤波方法存在着稳定性差、准确度下降等问题。本文结合传统高斯滤波的思想，提出一种加权的LiDAR点云滤波方法。该方法在雷达扫描点云数据过程中，根据数据点之间夹角的余弦值设置合理权重，从而较好地克服了上述问题。

1 改进的雷达点云滤波方法

本文使用的单线激光雷达如图1所示，在工作模式时，激光发射器在高速旋转的同时向外界发射激光，激光在碰到障碍物后返回[15]，接收器将接收到的光信号化为电信号并实时传送给雷达内部。该雷达是基于三角测距的原理，其扫描速度快、测距误差小、稳定性高、技术成熟。

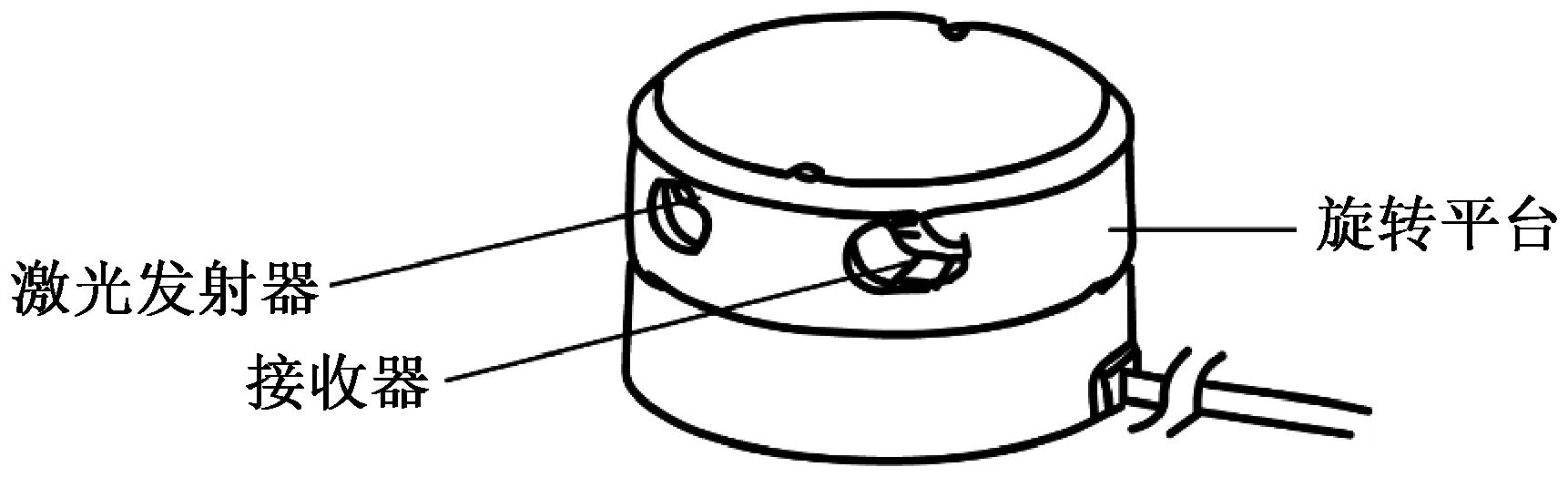
图1 激光雷达结构示意图Fig.1 Structural diagram of lidar

文中配置的激光雷达角度增量为0.003 456 rad，激光雷达的扫描范围是[-π/2, π/2]，每一帧扫描可获取909个激光扫描点，且每一个角度的激光扫描点上都有一个扫描距离与之对应。这些扫描数据点以极坐标形式返回测量数据，极坐标表示为

(1)

式中，ρn表示以角度增量为间隔第n个角度增量的方向上扫描到的物体的距离。

本文方法的测量数据是在笛卡尔坐标系下得到的，两者的转换关系如下。

(2)

式中，xn,yn为笛卡尔坐标系下雷达扫描点的坐标，文中n取909。

1.1 高斯滤波

当LiDAR 开始工作时，由周围环境反射激光点云产生点云信息，在获得的点云信息中含有大量的噪声，这些噪声总体为以下两个方面。第一个为LiDAR 传感器噪声，当 LiDAR 工作时激光旋转时产生的振动和出厂时的精度，影响了LiDAR 的测量效果；第二个为 LiDAR 工作时周围环境噪声。受到这些噪声影响，需要对点云进行处理。第二个噪声为本文的研究重点。

高斯滤波本质上是一种通过正态分布确定权重的线性平滑滤波，能够有效地抑制噪声，平滑数据，其实高斯滤波就是对LiDAR 扫描到的每一个点云数据进行加权平均之后再进行卷积的过程。传统的高斯滤波模板W定义为

(3)

式中f(x)定义为

(4)

高斯滤波结果表达式为

Ifiltered=W·I(xi)

(5)

扫描窗口的宽度定义为

x=lin space(-d,d,2·d+1)

(6)

式(5)与式(6)中，Ifiltered为当前滤波扫描点的距离值，x为当前窗口的宽度，d为窗口的半径，xi为窗口内排除极大值位置和无效点位置数据之后雷达扫描到的数据点位置，I(xi)为每个数据点对应的距离值。

本文传统高斯滤波方法中扫描点的高斯模板计算公式为式(3)和式(4)，公式中x为扫描窗口宽度，文中分别取σ=3，d=1。传统的高斯滤波方法中，默认每个数据点没有设置权值，以模板确定窗口宽度为3的数据点经高斯滤波后计算得到一个新的数据点，过程见式(5)。

高斯滤波的核心思想其实就是卷积过程，也就是将雷达扫描到的窗口中心点和左右数据与一个高斯模板进行卷积操作。本文设计中选择1×3的高斯模板。整个高斯滤波实现的过程就是随着选定的高斯模板的移动对雷达扫描到的环境中909个数据点(实际情况下可用的数据点一定小于909个)进行卷积处理，并将卷积之后某个数据点的高斯滤波值放到定义好的高斯模板中间位置，随后高斯模板继续基于中心点向后移动一个数据点位置。

高斯模板对整个数据进行卷积操作的过程中还需要考虑的地方有：909个点云数据的边缘情况，保证能取到1×3大小的窗口数据点；雷达扫描到的点云数据中存在的极大数据点和0值的点，这些数据点对高斯滤波是无效的，在与高斯模板进行卷积的过程中，注意窗口中排除不需要的数据点。为改进后高斯模板能扫描到完整的点云数据，以提取到的高斯模板中心位置不为零的数据点为中心起点，采用中心点前后位置以相同步长同时开始搜索的方法，判断同一时刻下前后位置数据是否为零，若同时不为零，模板扫描到的数据有效，若有一侧数据等于零，继续搜索，直到前后数据都不为零结束。高斯模板向后移动，以提取到的中心位置不为零的数据点为中心起点，重复此过程对每一个点云数据进行前后区域搜索。

对雷达扫描到的有效数据点在文中规定的窗口范围内重复上述过程，得到传统高斯滤波方法之后的扫描点数据，最后通过滤波得到的真实扫描数据结果如图2所示。

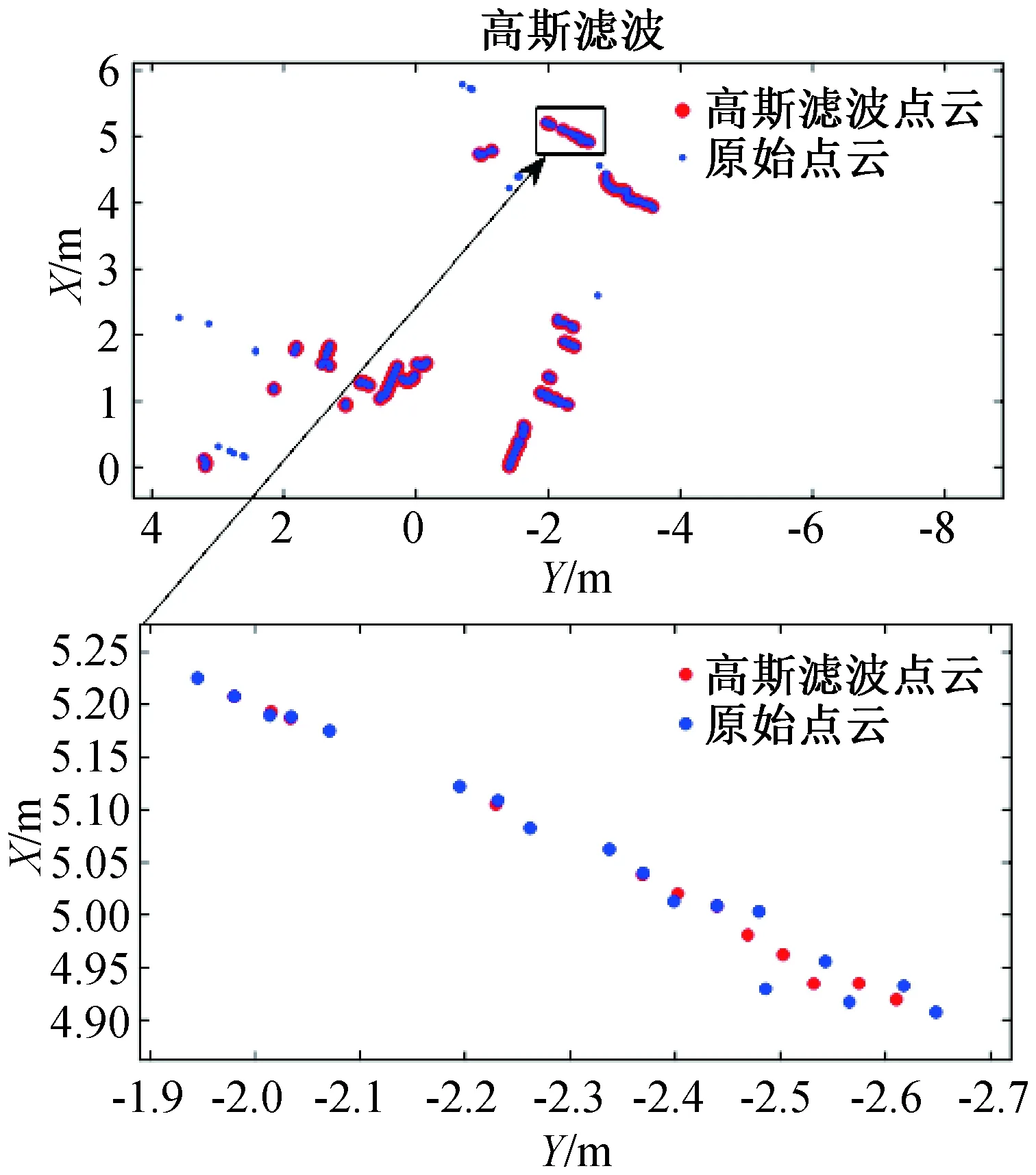
图2 点云高斯滤波Fig.2 Point cloud Gaussian filtering

图2中，蓝色点为激光雷达扫描到的室内原始数据，红色点为通过传统滤波之后得到的点云数据。通过滤波结果可以发现，初次滤波之后，离散程度较大的噪声点得到了一定程度的平滑处理，但是平滑效果还没有达到预期结果，需要进一步滤波。本文把传统的高斯滤波思想作为核心，提出一种新的滤波方法。

1.2 加权高斯滤波

根据传统的高斯滤波思想，为了调整窗口中心数据点的影响力，本文采用对雷达扫描到的点云进行加权滤波的处理方式，即对点云采用在传统高斯滤波的基础上再加一次权重的方法，减小雷达扫描到物体轮廓的波动，提高滤波方法准确性。雷达点云滤波方法流程如图3。

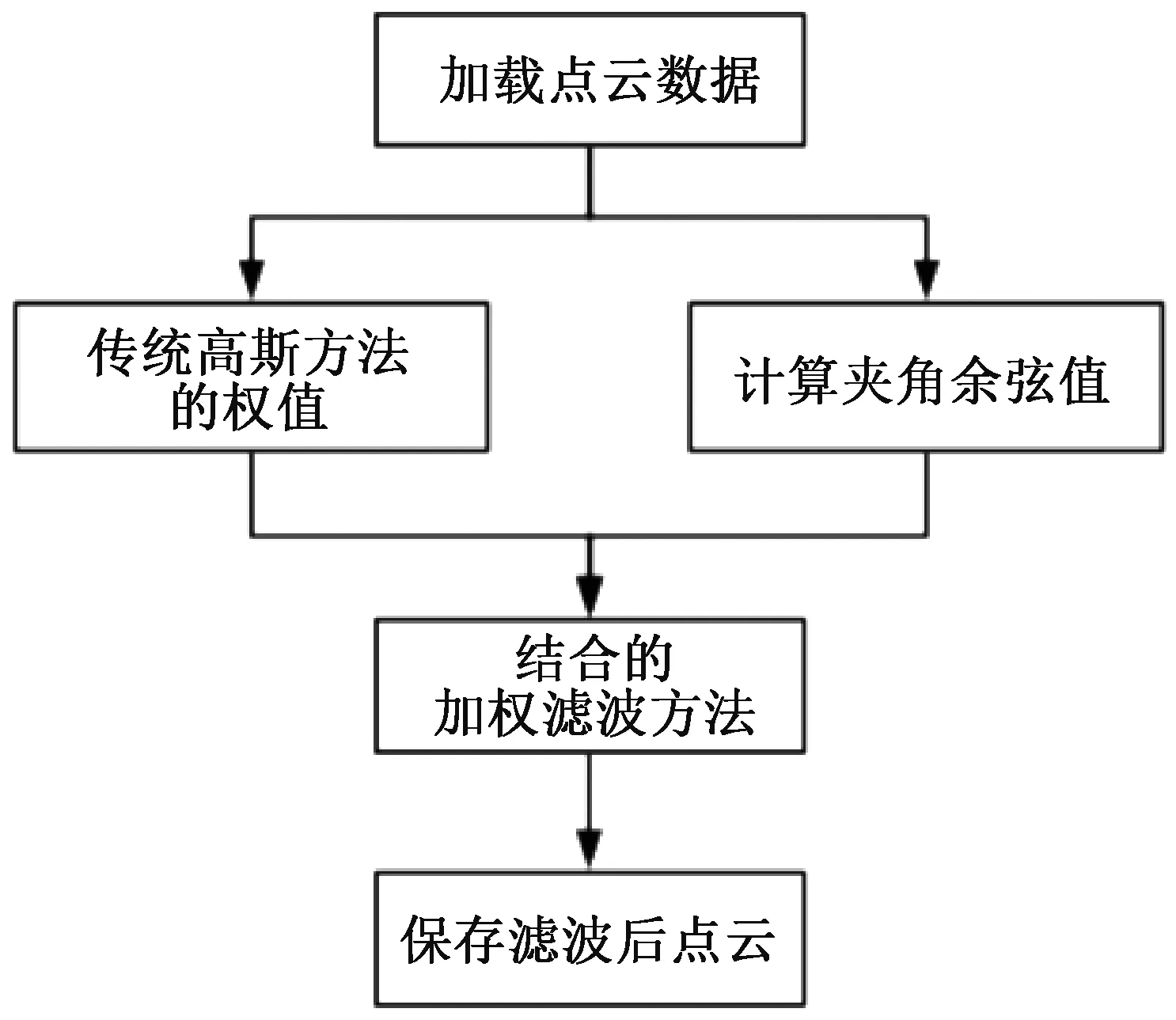
图3 点云滤波方法流程Fig.3 Gaussian filtering method flow

直接使用传统高斯滤波方法对雷达扫描到的数据点进行滤波，可以处理雷达点云中较明显的噪声，但是还存在离散波动较小的噪声。从matlab中导出的点云效果如图2所示的离散点分布可以看出，当离散数据点两两之间的夹角逐渐趋于180°时，点云的效果会更加平滑，对后续进行的使用雷达建图等效果也会更好。因此本文考虑从相邻数据点之间的夹角入手，对雷达扫描到的点云利用加权高斯滤波方法进行滤波处理，窗口内数据点之间夹角的大小决定了窗口中心数据点所赋的权值大小，并且以窗口中心数据点为起点，分别对左右两边数据点赋权值，保证窗口内各相邻数据点之间权值之和为1。

1.2.1 权值选取方法

由于在LiDAR 扫描到点云数据发生突变的数据点，数据特征变化随之较大，相邻数据点之间的夹角变化剧烈；相反的，在平滑区域的数据点，其数据特征变化比较平缓，所对应的数据点之间的夹角变化幅度较小。因此从相邻数据点间的夹角入手进行权值的选取是正确合理的。

由正态分布曲线可知，越接近中心取值越大，越远离中心取值越小。当数据点与相邻点之间的夹角在0°～90°范围时，夹角的余弦值是单调递减函数，即余弦值随着角度的增大而减小，从而使窗口中心位置数据点所占权重减小；当数据点与相邻点之间的夹角在90°～180°范围时，夹角余弦值的绝对值是单调递增函数，即余弦值的绝对值随着角度的增大而增大，窗口中心位置的数据点所占的权重就越大。

因此依据权重值参照正态分布选取的原则，并结合夹角余弦函数分布规律，采用窗口内相邻数据点之间夹角余弦值来作为滤波时窗口中心数据点的权值是合理的。

1.2.2 点云数据的权值计算

首先创建一个2m+1的窗口(文中m=1)，分别在窗口的中心数据点位置和左右两边数据点取值，取值为激光雷达在真实实验环境中扫描到的每个点云数据的角度与其对应的距离值，需要注意的是距离值必须为非0的有效值。并计算出相对于中心位置在窗口左右两端的斜率值k1,k2：

(7)

式(7)中x,y分别为极坐标系下的雷达扫描数据点对应直角坐标系下的x,y轴上的坐标。两段线段之间的夹角为

(8)

方法中加权高斯模板定为

(9)

式(9)中：

B=[(1+cosθ·c)·D(2)(a+

1)·D(1)(b+1)·D(3)]

(10)

∑B=(1+cosθ·c)·D(2)+(a+

1)·D(1)+(b+1)·D(3)

(11)

x=lin space(-d,d,2·d+1)

(12)

(13)

将改进后的窗口中间位置的数据点定义为

Ifiltered=W·I(xi)

(14)

式中，σ=3、d=1、a=-0.5、b=-0.5、c=-1，I(xi)是半径为d的窗口内每个数据点位置分别对应的距离值，Ifiltered是改进滤波方法之后的窗口中间位置的数据点对应的距离值。

根据上述公式可以知道，改进后的高斯滤波方法根据窗口内邻近区域点云的夹角余弦值来确定滤波之后点云位置的优化。因此，通过测试多次数值调整之后，由a，b，c的值对窗口内每个数据点的权重值进行了更加合理的分配，在对含有较小波动点云边缘信息的离散噪声进行滤波时尽可能使边缘信息得到平滑，提高了高斯滤波的准确性。

1.3 Harris角点检测

上文所述高斯滤波方法表明，扫描到的室内环境不平滑信息得到了一定程度的改进，为验证方法的可靠性，使用Harris角点检测的方法。Harris角点检测就是寻找扫描点中的极大值点来确定角点，具有一定的稳定性。Harris角点检测算法实现的步骤如下：

以单线激光雷达扫描到的点云数据作为输入值，计算扫描到的数据点u在X和Y方向两个上的梯度ux,uy：

(15)

计算数据点在两个方向上梯度的乘积：

(16)

(17)

式中w为高斯加权函数。图像u(x,y)在点(x,y)处平移(△x,△y)后的自相关函数可以近似为

c(x,y;Δx,Δy)≈AΔx2+2CΔxΔy+BΔy2

(18)

将自相关函数表示为椭圆方程：

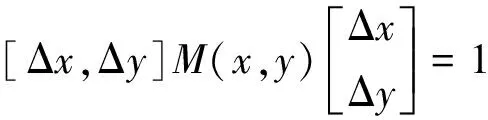
(19)

式(19)中计算每一个数据点的矩阵M：

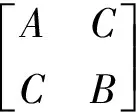
(20)

计算每个数据点的Harris角点响应值：

R=detM-α(traceM)2,α∈[0.04,0.06]

(21)

式中α为经验常数，文中α=0.06。每个数据点的角点响应值首先要大于阈值TR，计算公式为

TR=pr·Rmax

(22)

式中pr为角点响应比例系数，取pr=0.000 2，Rmax为遍历一帧点云后得到的最大角点响应值。

在点pi及其某一邻域D，D={pi|i∈(k-2,k+2)}，若点pk所对应的值在其邻域中为最大值且大于阈值TR，则保留pk的值作为提取到的角点。

2 实验结果与分析

2.1 实验数据采集

为了验证方法的适用性和可靠性，本文实验数据均来源于搭载在机器人上的单线激光雷达扫描仪，为得到真实实验室室内环境点云数据，通过真实的机器人平台得到雷达扫描到的点云数据，对所处实验室内扫描的点云进行滤波处理。机器人使用两轮差速运动底盘，搭载了激光雷达、工控机等设备，实验环境是Windows10，64位操作系统，实验软硬件参数配置见表1。

表1 实验软硬件参数配置

图4 实验环境Fig.4 Experimental environment

本文的实验环境如图4 (b)所示，真实环境下雷达实时扫描到的点云图见图2。环境中存在着一些桌子、墙面等简单特征物体，对应扫描点云图中的圆弧和线段特征，也存在杂乱电线、形状较复杂的椅子腿等复杂物体。真实实验环境中，使用搭载在机器人上的激光雷达实时扫描得到室内点云数据，首先对原始的室内点云数据进行加权高斯滤波改进，然后再进行角点特征提取。实验在不同场景下从滤波方法优化效果对比、角点提取结果和距离测量上，验证本文滤波方法的稳定性和准确性。

2.2 实验结果与分析

本文采用matlab2019a进行编程并进行实验仿真，对激光雷达采集到的点云数据利用经典的高斯滤波方法和加权滤波方法对数据进行滤波处理。两种方法的滤波效果对比如图5所示。

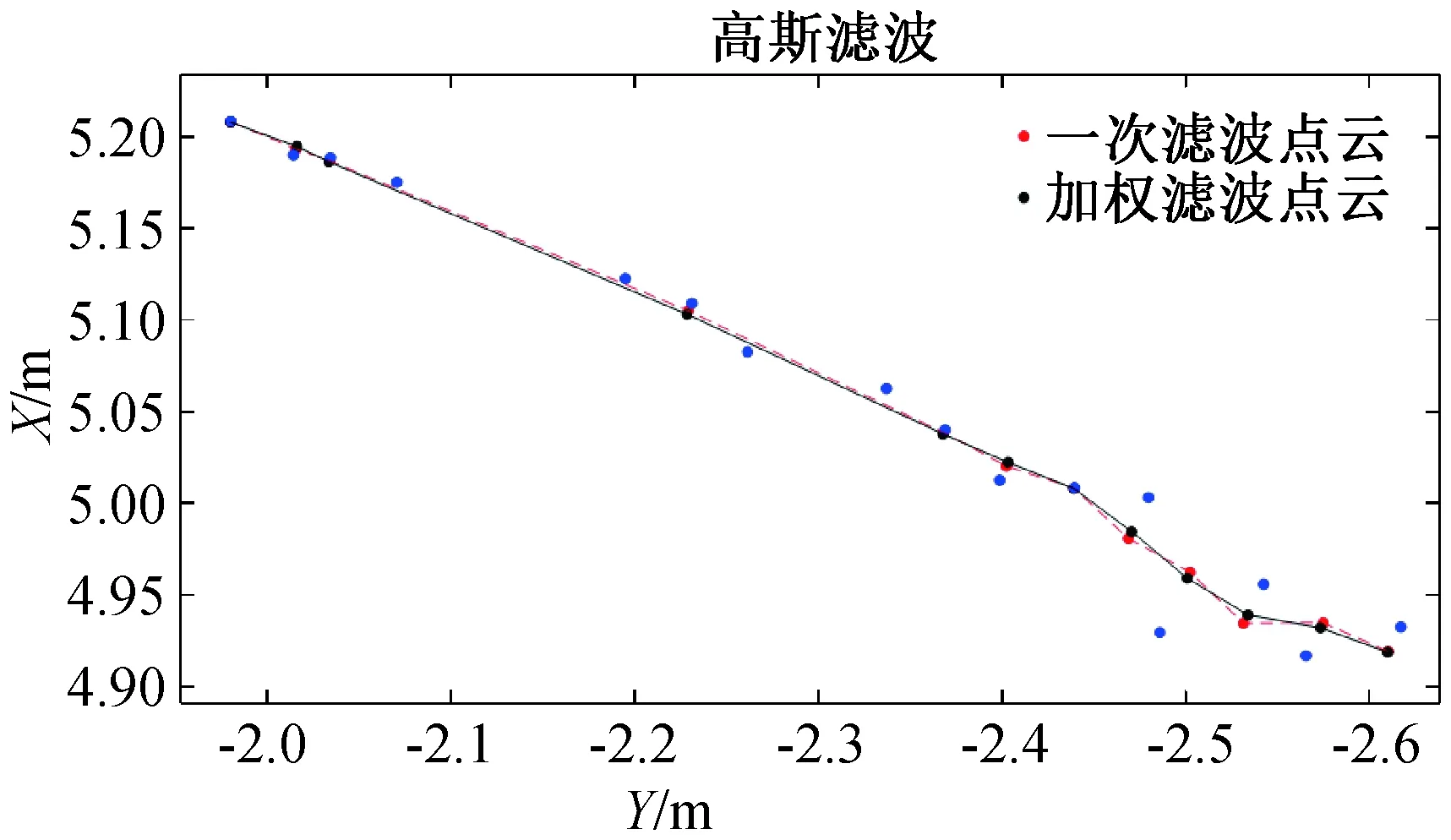
图5 两种滤波方法的点云效果对比Fig.5 Comparison of point cloud effects between two filtering methods

图5中蓝色散点为原始点云，红色线段为原始高斯滤波后点云的平滑效果，黑色线段为加权高斯滤波后点云的平滑效果。原始点云受到噪声等影响之后，由雷达扫描到的物体轮廓会发生波动，经过高斯加权滤波之后，通过黑色线段和红色线段对比的平滑效果可以看出，离散点较小的波动也得到了更好的抑制，物体边缘点云更加平滑。

为了验证本文滤波方法的适用性，在实验室环境里，对另一种场景进行滤波和角点提取的测试，图6为实验室拍摄的真实场景图。将基于传统高斯的点云滤波结果、加权点云滤波结果与相同区域内原始点云进行对比分析，统计如图7所示，图中蓝色散点为原始点云，黑色线段为加权高斯滤波之后点云平滑效果。

图6 实验环境及点云分布Fig.6 Experimental environment and point cloud distribution

相对于雷达扫描到的原始点云，从不同场景实验环境对比中可得改进后点云平滑效果更好，为了验证改进的高斯滤波方法的稳定性，在本次实验场景下进行角点提取测试。角点检测如图8所示。

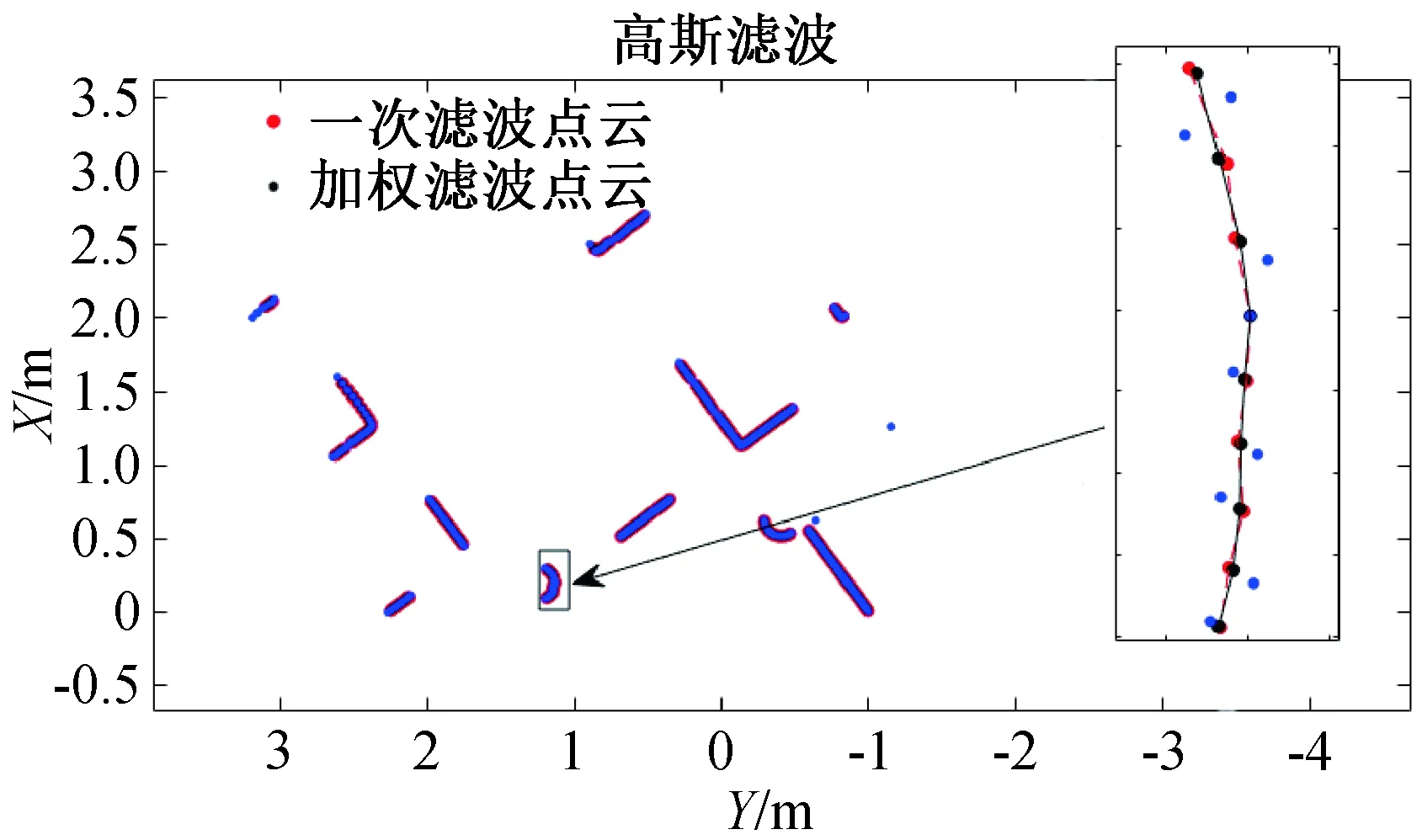
图7 滤波效果对比图Fig.7 Comparison diagram of filtering effect

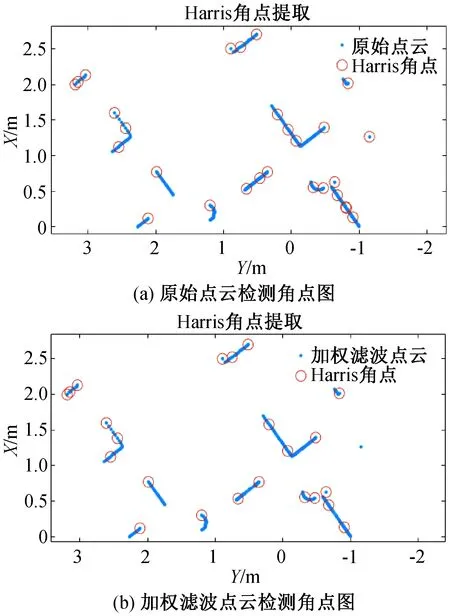
图8 点云角点检测结果Fig.8 Point cloud corner detection results

由图8提取结果可得，从原始点云数据中提取的角点数量为28个，经过加权滤波方法处理后，角点提取数量减少到了23个，改进后的滤波方法产生的数据点云检测出的角点数比初始点云提取出的角点数要少。原因是我们需要的主要是特征边界处的角点，但使用原始点云进行角点提取时，把连续的数据点中一些波动幅度较大的点也当作Harris角点提取出来。使用加权滤波的方法后，平滑了雷达扫描到的数据点，因此所能提取到的角点数就变少了，结果对噪声敏感度降低，相对较准确。

图6(b)中，取一段激光雷达扫描到的物体边缘信息直线段“L1-L2”，计算此时雷达扫描中心到物体平面边缘信息的距离和雷达扫描中心到初始点云的距离，重复测量100次，每次距离值统计结果如图9所示。由图9可得，相比于原始点云的测距结果，使用本方法处理之后，结果更加稳定，雷达扫描之后得到的数据更加准确。

图9 本文方法与原始点云数据测距对比图Fig.9 Comparison between this method and original point cloud data

图9中，蓝色线段为使用原始点云得到的距离值，红色线段为使用本文改进滤波方法之后得到的距离值。这两次实验中分别统计测量均值、标准差和平均绝对误差(以均值为参考值)，如表2所示。由表2可得，通过本文方法处理点云之后，绝对平均误差更小，说明加权滤波方法有效提升了雷达扫描准确性。

综上可得：由激光雷达扫描到的原始点云信息，数据点离散程度大，且角点检测时把一些波动幅度较大的点也当作Harris角点检测出；通过传统高斯滤波方法，边缘信息数据点的离散程度得到了一定的优化，但是还存在一定的波动；而加权高斯滤波方法，相对于传统滤波方法它使点云数据的波动再一次得到了抑制，较好的角点检测结果验证了改进滤波方法的可靠性，点云测距结果验证了准确性。因此，加权滤波方法有效提升了激光雷达扫描点云滤波过程中的问题，有助于之后激光雷达局部建图效果。

表2 点云测距结果统计

3 机器人操作系统的加权高斯滤波方法实现

本文在机器人操作系统(Robot Operating System, ROS)平台上，改进的高斯滤波方法优化了建图时接收到的激光雷达数据，实现了机器人的增量式地图构建，在构建实验室环境地图时，需要输入优化之后的激光雷达数据信息和机器人行驶过程中产生的坐标信息，启动所需的建图节点之后，就会订阅这两个信息产生的话题，订阅和发布的话题如表3所示。

表3中的机器人坐标信息tf树表示机器人在实验室环境建图过程中所需要的坐标系，它是已经定义好的，机器人在行驶的过程中一定要保证tf坐标是连通状态，也就是说建图过程中要订阅相应的tf变换，即订阅激光雷达到机器人底盘坐标系、机器人底盘到里程计以及里程计到地图坐标系的tf，由tf static_transform_publisher定期广播插入到tf树中，保证tf树处于连接状态，这样才能完成机器人在建图过程中的坐标系转换。

表3 建图订阅与发布的话题

雷达发布的激光数据：本文加权高斯滤波方法优化之后的激光数据，是建图过程中必要的环境信息，由909个激光扫描点中有效的数据点组成，激光雷达节点发布，建图节点订阅。

地图信息：全局地图坐标系，消息类型为nav_msgs/OccupancyGrid，由建图节点Gmapping发布。

基于ROS平台，本文的实验场景为电气楼研究生工作室，传统的激光雷达获取的点云数据存在噪声点问题，噪声点不处理则会在机器人建图中产生负面影响，在建图时可能会在没有物体的栅格上出现障碍物或建图得到的物体边缘信息不够平滑。因此移动机器人需要使用改进的激光雷达点云滤波方法，在实验室真实场景下进行建图实验，最终获得局部二维栅格地图。建图过程如图10所示。

从实际建图效果和二维激光雷达本身的特性来看，基于Gmapping的建图方式存在如下几个问题：

(1)无法探测到的区域问题。因为激光雷达能够扫描到的平面范围取决于激光雷达在机器人上的安装高度，图10(a)的椅子经测量最低处平面高度为50 cm，机器人雷达扫描高度为16.5 cm，相机高度为57.3 cm，椅子支撑部分宽度大于机器人宽度。类似场景中，物体表面在视觉范围内但高于激光雷达安装高度，雷达扫描建图时，只能扫描到椅子的支撑部分如图10(a)中红框。会影响机器人的通行效果使机器人产生碰撞。

(2)无法探测到玻璃材质的门窗。因为激光雷达的特性，探测到玻璃材质物体时，发射出的红外激光无法穿透，不能接收到玻璃上发出的反射激光，从而导致建图出现差错。

针对上述问题，需要结合视觉来丰富机器人获取周围环境信息的能力，因此此处只需要获取局部二维栅格图即可。

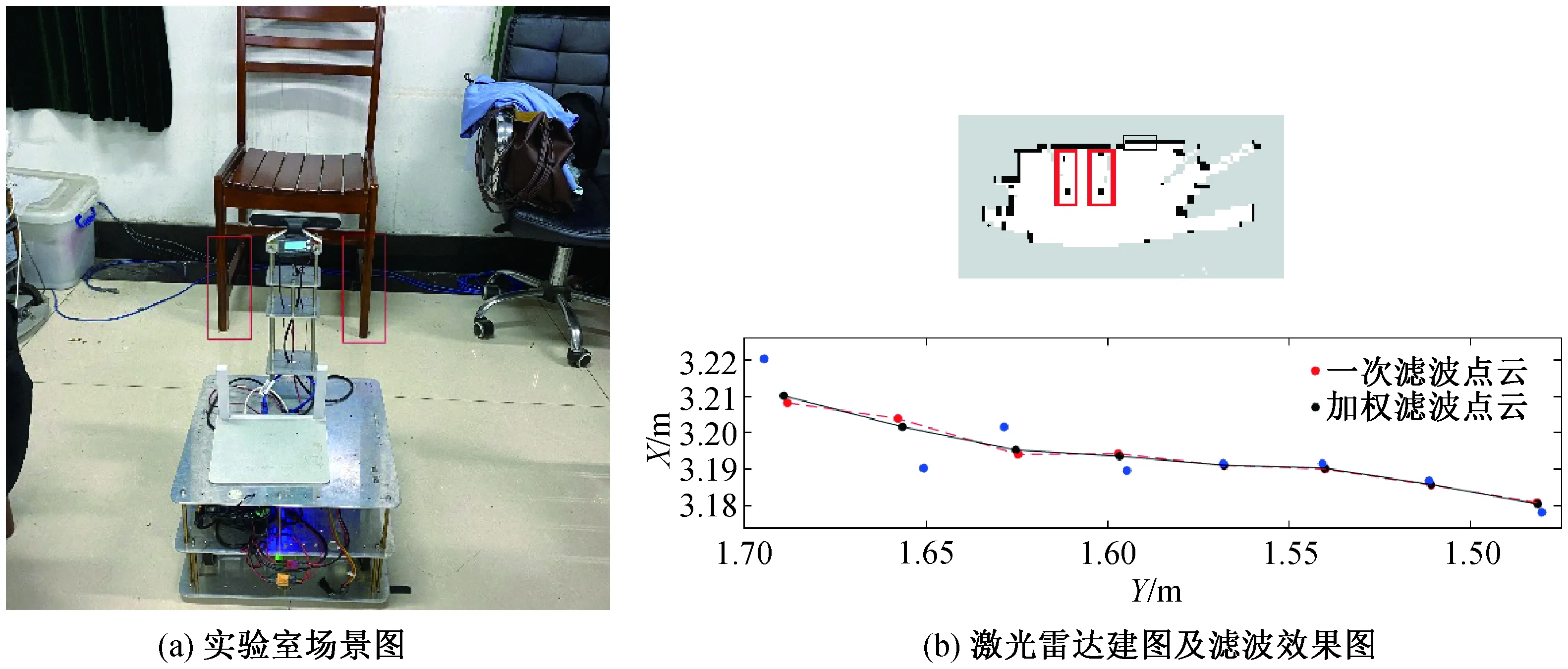
图10 建图环境及结果Fig.10 Mapping environment and results

4 结论

本文提出一种以高斯滤波方法为基础，以角度余弦为加权值的滤波方法，改进后绝对平均误差较改进前减少到了0.000 2，滤波准确性更高，且点云数据离散程度更加平滑，稳定性更高。最后将本文方法应用到实际机器人操作系统底盘中实验结果表明，改进后的滤波方法准确性高，适应环境能力较好，满足机器人雷达点云滤波需求。