基于改进SSA-BP神经网络的复烤水分和温度预测
王浩陈婷陈兴侯陈明高兴宇马显滔范振宇
(1.昆明理工大学机电工程学院,云南 昆明 650504;2.云南烟叶复烤有限责任公司麒麟复烤厂,云南 曲靖 655000)
引言
打叶复烤是初烤后的再加工过程,烟叶经过复烤,理化性质进一步发生变化,内在品质提高,有利于长期贮存和适应卷烟工业的使用需要。所以复烤作为卷烟加工中必不可少的环节,其技术的提升对烟叶加工有着重要意义。随着技术的不断发展,复烤生产线利用模糊控制、电控系统、先进控制算法和多策略复合控制等技术实现了生产线加工的自动化,如今复烤企业要求提高,自动控制也正向着智慧控制的方向发展。其中一个重要问题就是加工一致性问题,即在传统加工中由于人工经验不同,导致复烤设备设置的加工参数不一样,使得成品烟叶水分和温度不同,从而影响烟叶品质,造成品吸感觉不同。基于此,许多学者进行了研究。
有学者从化学成分方面入手,分析烟叶化学成分,从而得出应该采用的工艺参数。马亚萍[1]等研究了复烤对四川凉山地区烟叶多酚含量的影响,得出烟叶香气感官质量最优的打叶复烤参数:一润出口温度为60℃、复烤一区温度为50℃、复烤二区温度为79℃、复烤三区温度为67℃、复烤四区温度为70℃、醇化时间12个月;胡静宜[2]等研究了复烤后不同尺寸烟叶化学成分差异;李庆祥[3]等研究了不同工序对烟叶糖碱比的影响。也有学者通过直接实验的方法,明确参数设置依据。白万明[4]通过单因素实验,对加料比例、阀门开度等进行实验,确定了料机内的蒸汽阀门开度40%和60%较为合适。朱贝贝等[5]利用均匀设计方法,经过试验分别得出了上、中、下部烟感官质量最高时的干燥区温度。还有学者从烟叶物理特性出发,研究均质化加工和物理特性关系。王戈[6]引入颜色特性和光谱特性作为调控因子,分析了不同调控模式下复烤的均质化效果。
总的来说,这些研究虽然从不同角度都促进了复烤技术的提升,但是都存在一些不足之处。其都是针对复烤的某个环节,是从局部而不是整体考虑技术的提升;都需要进行实验,对复烤企业有负担且不方便,甚至有的是针对特定产地烟叶,因此不具有普适性和推广性;最重要的是,并没有直接给出参数和质量指标之间的关系。综上所述,将参数设置依据转化为具有普适性并且可以量化的标准依然是一个亟待解决的问题。
建立预测模型反映输入输出关系,可以在复烤之前预测结果,并且不必专门实验,以平常加工中得到的数据即可分析,能较为直观地为参数设置提供可靠依据。复烤中存在许多非线性问题,且数据之间没有明确数学关系,运用神经网络可以较好地解决该问题。
人工神经网络无需知道输入和输出的数学方程,通过训练即可得到期望的输出。其中BP神经网络是应用最广泛的神经网络之一,其具有优良的多维函数映射和非线性映射能力,适合运用到寻找复烤参数的输入数据与输出数据的映射关系。基于此,本文提出用改进的麻雀搜索算法优化初始权重和阈值,建立BP神经网络预测模型,找到复烤输入参数和输出结果的映射关系,为输入参数设置提供依据。最后以麒麟复烤厂某个批次的加工数据作为研究对象,将预测模型运用到其中,验证效果。
1 工艺分析
复烤技术由国外传入国内,20世纪60年代开始挂杆复烤转变为打叶复烤,如今随着技术和工艺的不断发展,已经逐步实现全面机械化和自动化加工。复烤是一个复杂的过程,涉及多种物理和化学变化,现简要分析复烤的部分工艺阶段,并选择了研究的工艺参数和控制指标。
1.1 流程分析
复烤车间流水线可粗略分为润叶、风分、干燥、冷却和回潮5个阶段,流程如图1所示。其中,从仓库到风力除杂等步骤为预备阶段,烟叶从烟筐中转移到铺叶台,然后经过人工筛选将烟叶中的非烟物质初步去除,接着机器把大片烟叶切断,再通过机器二次风力除杂,流量称可以检测流水线上烟叶的重量,保证加工时烟叶的量在机器承受范围内。预备阶段处理是为了后续更好的加工。
从打叶风分开始,为复烤主要阶段。打叶风分主要涉及的是烟叶物理形态变化(烟叶叶片和梗的分离),就不作为分析对象。复烤厂现在逐步采用“直接复烤”技术,即烟叶在干燥段被加工到指定水分含量和温度,经过冷却就符合要求,不用回潮,因此减少了回潮段的蒸汽使用量,大幅度节约成本,所以回潮段也不作为分析对象。综上,选择润叶、干燥以及冷却3个阶段数据建立预测模型。
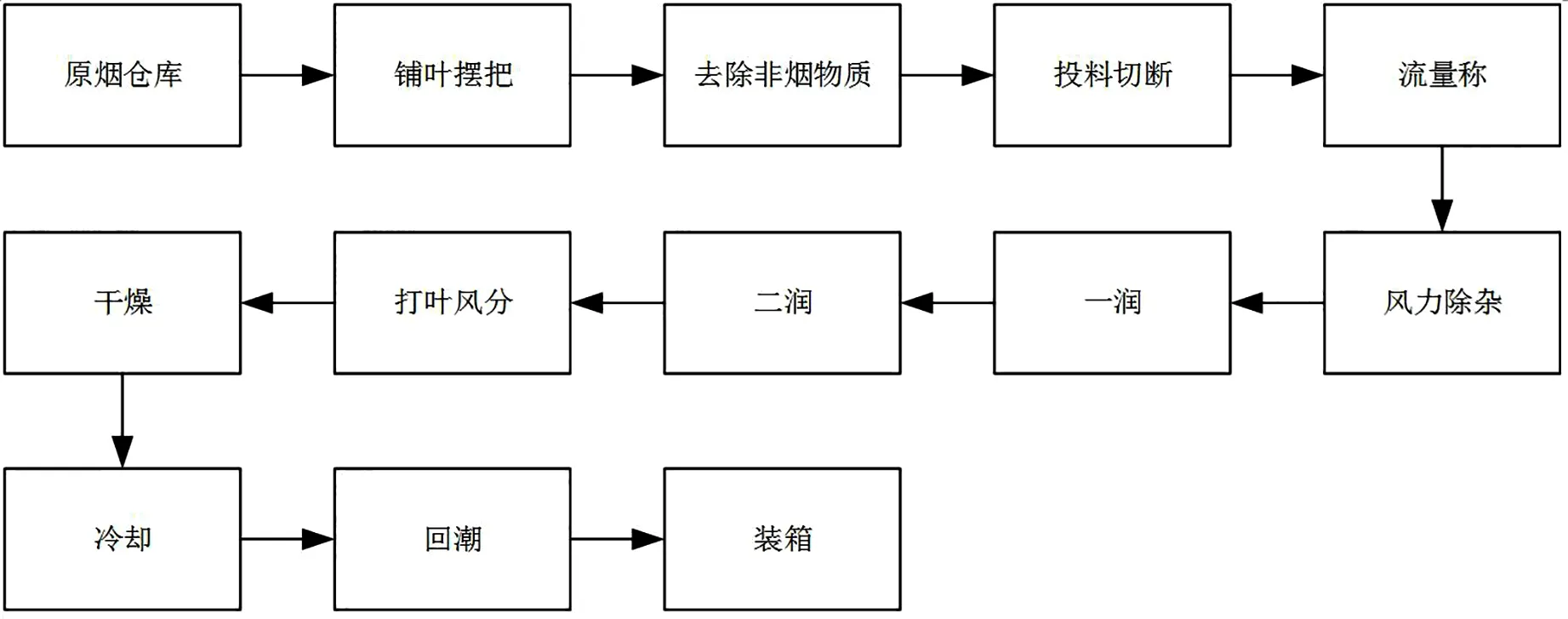
图1 复烤工艺流程
1.2 材料选择
烟叶材料选自麒麟复烤厂2020年某个批次加工数据,选取经过工业分级后的普洱(墨江)C3F单打烟叶,数据由加工时复烤设备记录,真实可靠。
1.3 控制指标
复烤加工时,每个阶段开始和结束都会测量烟叶的含水量和温度,这2项指标在复烤时至关重要[12]。水分过大时,不利于烟叶的储存,容易霉变;水分过低,则会增加烟叶脆性,导致碎烟率上升、大中片率降低等一系列问题。温度不仅会影响烟叶水分,还与烟叶化学成分(如pH值[13]、烟碱值[14]等)变化密切相关,而烟叶化学成分直接决定了其内在品质。所以将出口温度和水分这2项数据作为模型的控制指标,复烤厂对其要求如表1所示。因为要对整个复烤环节进行研究,探究每个阶段的参数对于最后成品的含水率和温度影响,所以中间过程就不予考虑,只将最后阶段的叶片含水率和温度作为模型的期望输出。
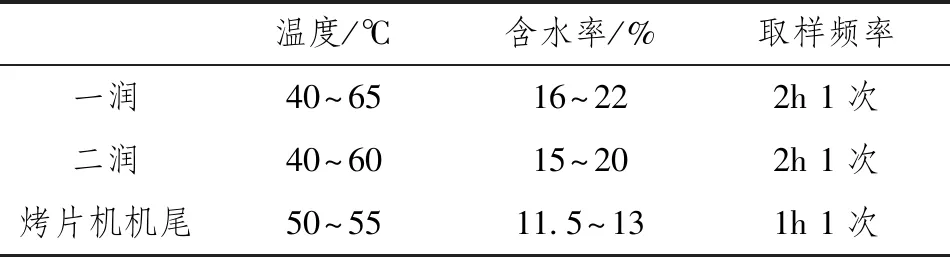
表1 质量要求
1.4 工艺参数选择
从流程分析可确定研究阶段为润叶、干燥和冷却,根据每个阶段各特点和复烤厂实际需求选择特征输入,即选择流量称实际值、一润热风温度、一润回风温度、一润散热蒸汽压力、二润散热蒸汽压力、二润热风温度、二润回风温度、烤片机一区加水量、烤片机二区加水量、烤片机三区加水量、冷却区温度、冷却区水分、干燥一区温度、干燥二区温度、干燥三区温度、烤片机入口温度、烤片机入口水分17个作为工艺参数。
需要特别说明的是,烤片机是加工的最后阶段,入口的水分和温度与出口水分和温度密切相关,所以烤片机入口温度和水分也作为输入变量;工艺参数太多,不好一一列举,故只展示部分,部分参数指标如表2所示。
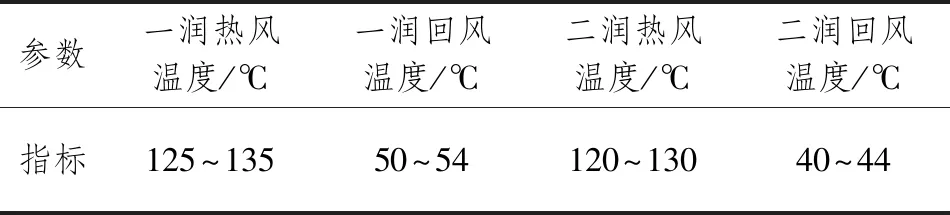
表2 部分工艺参数指标
2 模型建立
人工神经网络通常也被称为平行分布式处理模型,具有高度自适应性和容错性,并且其优越的非线性模拟能力也很突出,使得在预测、控制等方面有很多应用。复烤环节工艺参数众多,与控制指标之间没有明确数学模型,建立神经网络模型能有效根据输入预测输出。
2.1 神经网络原理
人工神经网络是一种旨在模仿人脑结构及其功能的由多个非常简单的处理单元彼此按某种方式相互连接而形成的计算机系统,BP神经网络亦是如此,其学习过程由信号的正向传播与误差的反向传播2个过程组成。正向传播时,输入样本从输入层传入,经隐层逐层处理后,传向输出层。若输出层的实际输出与期望输出不符,则转向误差的反向传播阶段。误差的反向传播是将输出误差以某种形式通过隐层向输入层逐层反传,并将误差分摊给各层的所有单元,从而获得各层单元的误差信号,此误差信号即作为修正各单元权值的依据[7-14]。BP网络由输入层﹑输出层和隐层组成,结构如图2所示。
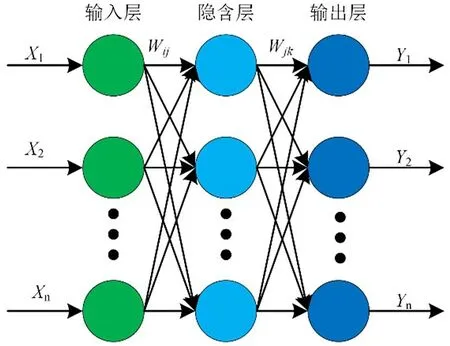
图2 BP神经网络结构
假设输入层的节点个数为n,隐含层的节点个数为l,输出层的节点个数为m。输入层到隐含层的权重为wij,隐含层到输出层的权重为wjk,输入层到隐含层的偏置为aj,隐含层到输出层的偏置为bk。学习速率为η,激励函数为g(x)。隐含层的输出Hj:
(1)
输出层的输出:
(2)
令期望Yk为期望输出,记ek=Yk-Ok,网络总误差:
(3)
其中,i=1…n,j=1…l,k=1…m。权值更新公式:
(4)
2.2 训练网络
将总样本数中的3/4数据作为训练集,1/4为测试集。以工艺参数作为特征输入,以控制指标作为期望输出。设置学习速率为0.01,训练最小误差为0.0001,迭代次数为1000次。
隐含层节点数根据经验公式(5)确定:
(5)
式中,h为隐含层节点数;r和e分别为输入层和输出层节点数;s为1~10常数。根据经验公式(5)计算得隐含节点最大、最小值,然后通过试验,求每一个节点数下训练集均方误差,取均方误差最小的隐含节点数作为神经网络隐含节点数。
训练步骤如下。Step1:初始化网络的权值和阈值;Step2:导入训练样本;Step3:前向传播计算;Step4:误差反向传播计算并更新权值;Step5:迭代,用新的样本进行步骤3和4,直至满足停止准则。
流程如图3所示。
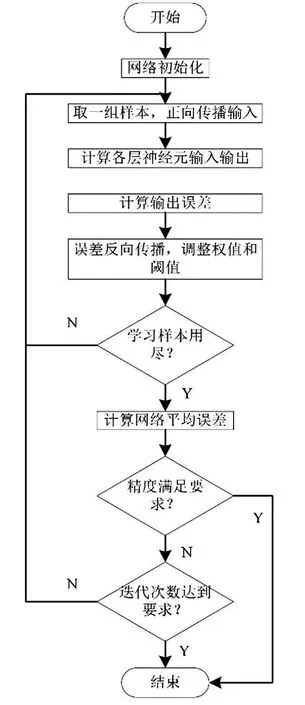
图3 神经网络训练流程
3 优化算法
麻雀搜索算法(Sparrow Search Algorithm,SSA)[15]是一种新型的群智能优化算法,主要是受麻雀的觅食行为和反捕食行为的启发。麻雀种群在觅食过程中分为发现者与加入者2部分,分别负责提供种群觅食的方向以及追随并获取食物。当麻雀种群意识到危险时,则会发生反捕食行为并更新种群位置。
3.1 算法原理
麻雀搜索算法具有良好的局部寻优能力和稳定性,其实现原理如下。初始由n只麻雀组成的种群表示形式:
(6)
式中,d表示待优化问题变量的维数;n为麻雀的数量。则所有麻雀的适应度值表示形式:
(7)
式中,f表示适应度值。在SSA中,具有较好适应度值的发现者在搜索过程中会优先获取食物。发现者的位置更新描述如下:
(8)
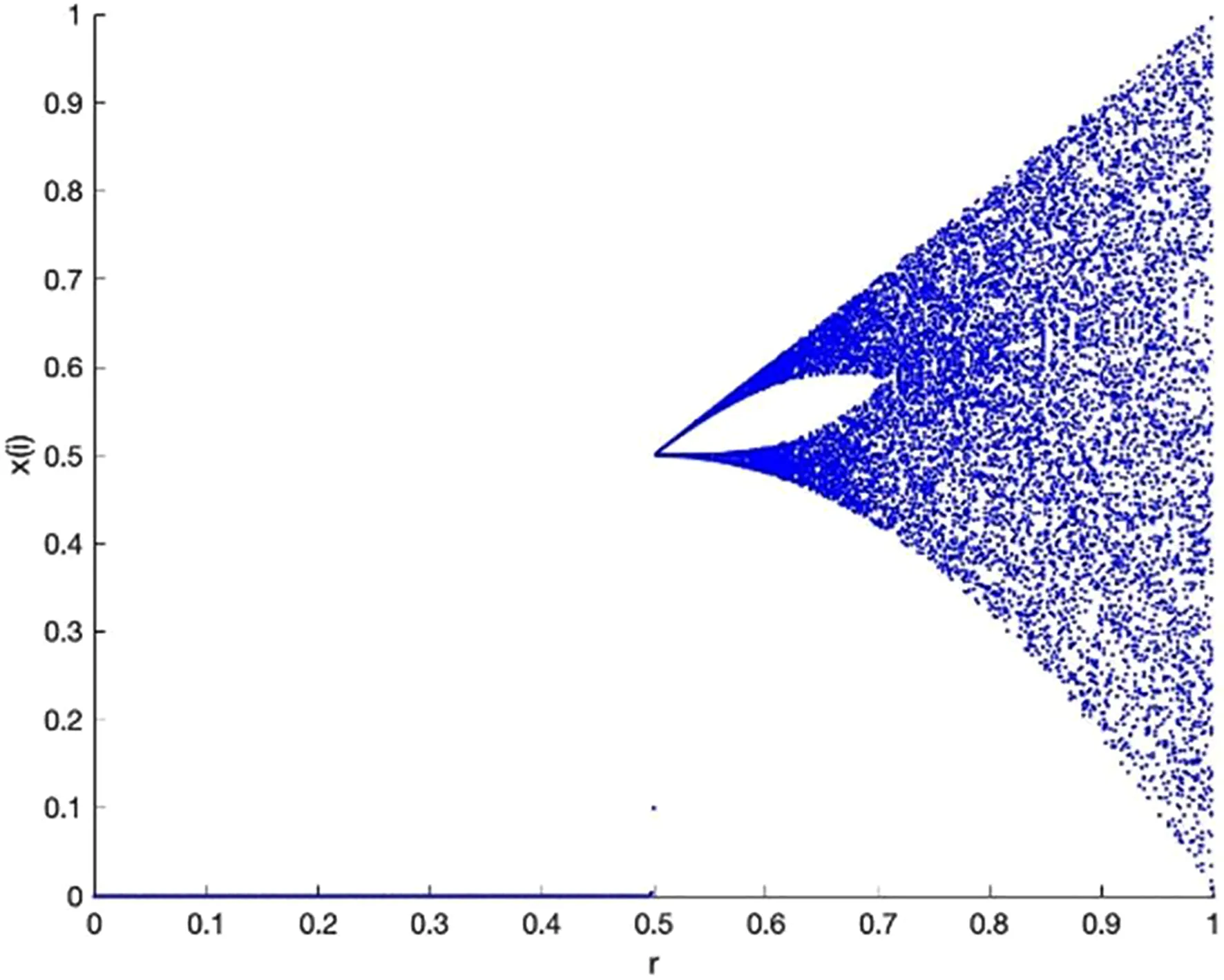
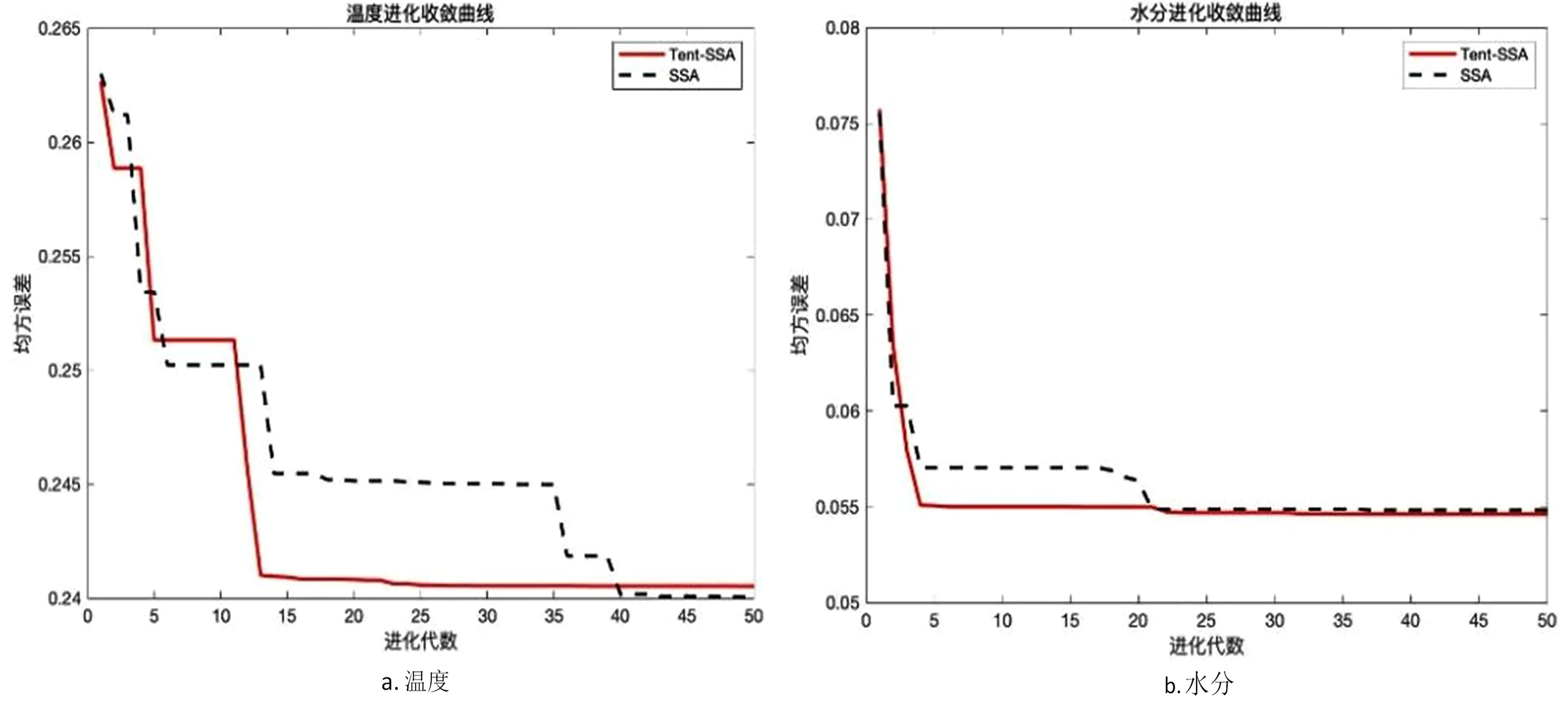
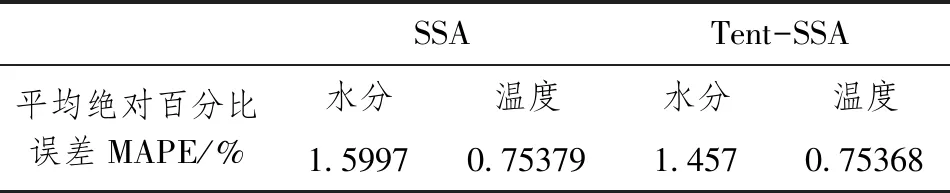
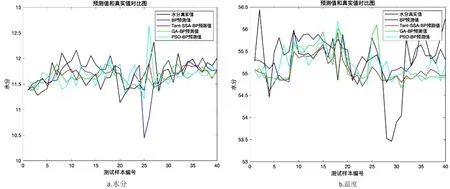
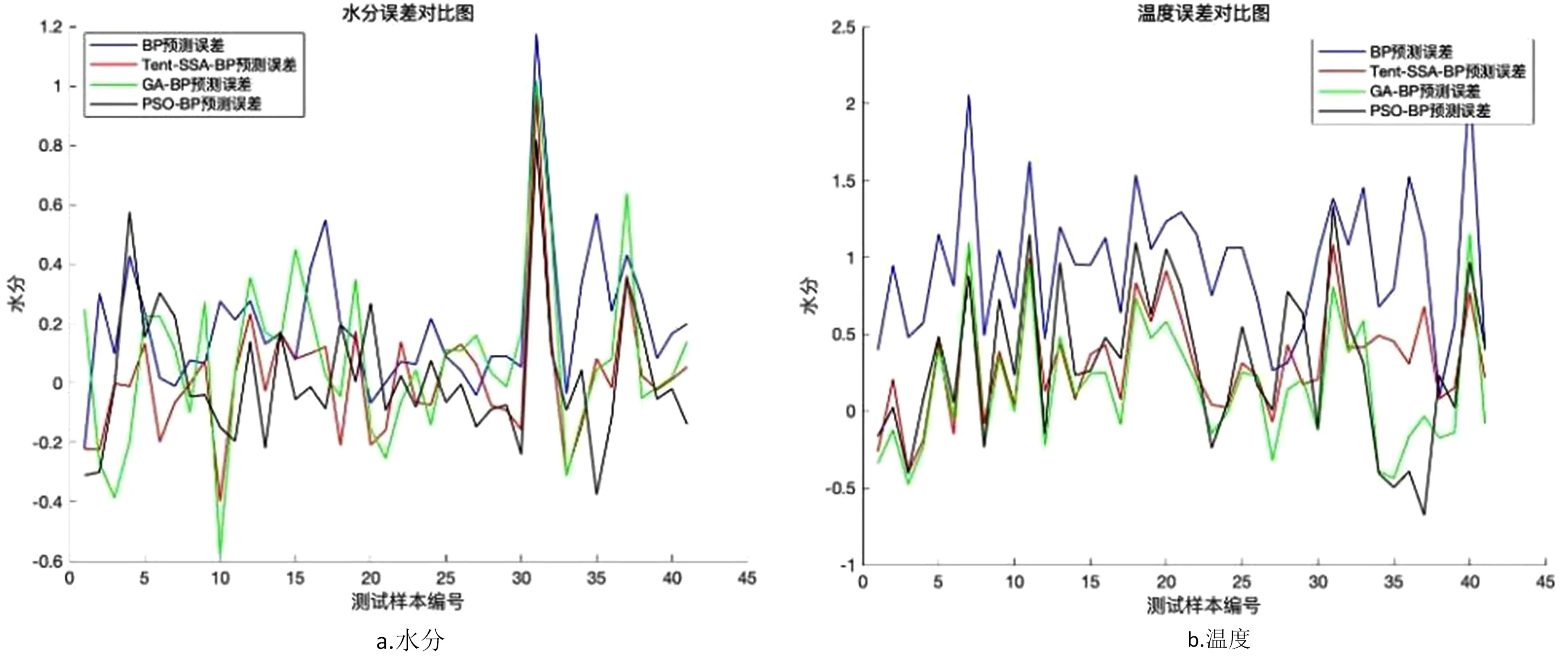
式中,t代表当前迭代数;j=1,2,3,…,d;itemmax是一个常数,表示最大的迭代次数;Xi,j表示第i个麻雀在第j维中的位置信息;α∈(0,1]是一个随机数;R2(R2∈[0,1])和ST(ST∈[0.5,1])分别表示预警值和安全值;Q是服从正态分布的随机数;L表示一个1×d的矩阵,其中该矩阵内每个元素全部为1。当R2 (9) 式中,XP是目前发现者所占据的最优位置;Xworst表示当前全局最差的位置;A表示一个1×d的矩阵,其中每个元素随机赋值为1或-1,A+=AT(AAT)-1。当i>n/2时,表明适应度值较低的第i个加入者没有获得食物,处于十分饥饿的状态,此时需要飞往其它地方觅食,以获得更多的能量。反捕食行为,更新麻雀种群的位置如下: (10) 式中,Xbest是当前的全局最优位置,也是十分安全的;β作为步长控制参数,是服从均值为0,方差为1的正态分布的随机数;K∈[-1,1]是一个随机数,表示麻雀移动方向同时也是步长控制;fi是当前麻雀个体适应度;fg和fw是当前全局最佳和最差适应度;ε是常数,避免分母为零;当fi>fg表示此时的麻雀正处于种群的边缘,极其容易受到捕食者的攻击;fi=fg时,表明处于种群中间的麻雀意识到了危险,需要靠近其它麻雀以尽量减少其被捕食的风险。 算法步骤如下。Step1:初始化种群、迭代次数、初始化捕食者以及加入者比列;Step2:计算适应度值并且排序;Step3:利用式(8)更发现者者位置;Step4:利用式(9)更新加入者位置;Step5:利用式(10)更新警戒者位置;Step6:计算适应度值并更新麻雀位置;Step7:是否满足停止条件,满足则退出,输出结果;否则,重复执行Step2~6。 从上述可知,麻雀搜索算法的初始种群位置是随机的,这种方式生成的种群多样性较差,可能导致算法陷入局部最优解,影响收敛速度和精度[16,17]。混沌是一种确定的系统中出现的无规则的运动,将其引入算法中,能较好解决该问题。 本文采用Tent混沌映射函数,其具有分布均匀、不可重复、不确定性和遍历性等特点。Tent映射混沌分岔图如图4所示。当系统的参数不断连续变化时,每跨过一点复杂程度都会成倍增加,直到一点系统突然变得不规律,即系统跨入混沌。此时将Tent映射生成的数据作为初始麻雀种群的位置信息既能保持多样性,从而避免局部最优解,也能提高收敛速度和全局搜索能力[18,19]。 图4 分岔图 3.2.1 Tent混沌序列 单梁[20]等研究表明,Tent映射可以作为产生优化算法的混沌序列,并且其遍历均匀性和收敛速度优于Logistic映射,其表达式: (11) 经过贝努利位移变换后: zi+1=(2zi)mod1 (12) (13) 相应的贝努利位移变换式为: (14) 式中,NT为混沌序列内的粒子个数;rand(0,1)为[0,1]之间的随机数。 3.2.2 改进流程 改进的步骤如下。Step1:初始化麻雀搜索算法的参数,包括种群数量、预警值、安全值等;Step2:利用Tent混沌映射函数生成均匀分布于整个解空间中的混沌序列,即种群初始位置;Step3:计算每只麻雀的适应度值,确定解空间中适应度值最优和最差的麻雀个体的位置;Step4:确定麻雀种群中发现者的数量,根据公式(8)计算其更新过后的位置;Step5:确定麻雀种群中加入者的数量,根据公式(9)计算其更新过后的位置;Step6:确定麻雀种群中意识到危险的个体数量,根据公式(10)计算其更新过后的位置;Step7:计算每只麻雀的适应度值,与之前的适应度值进行比较,若新的适应度值更优则更新;Step8:如果达到算法的最大迭代次数,则输出全局适应度值最优的麻雀的位置信息;否则转到第4步继续执行。 在BP神经网络中,初始权值和阈值是在一个固定范围内随机产生的,初始权值的选择对于局部极小点的防止和网络收敛速度的提高均有一定程度的影响,如果初始权值范围选择不当,学习过程一开始就可能进入“假饱和”现象,甚至进入局部极小点,网络根本不收敛。本文采用改进的麻雀搜索算法就是通过计算得到最优的初始权值与阈值,提高BP神经网络的收敛速度和精度,以达到期望的效果,优化流程如5所示。 图5 优化流程 本文的实验数据来自麒麟复烤厂,经过筛选共得到480组数据,前360组作为训练集,后120组作为测试集。17个工艺参数作为神经网络的输入,水分和温度作为输出。 均方误差是反映预测量和被预测量之间差异的一种度量,其越小说明预测效果越好,计算公式: (15) 表3 试验结果 为了证明所提算法的优越性,还使用了粒子群算法(Particle SwarmOptimization,PSO)、遗传算法(Genetic Algorithm,GA)进行优化,最后对比结果,为了保证公平,同一参数设置相同,而关键参数设置如表4所示。 表4 对比算法参数选择 设置好参数后,将数据导入到标准BP模型、Tent-SSA模型、GA-BP模型和PSO-BP模型中,进行精度和稳定性分析。 4.2.1 改进前后对比 图4为SSA-BP模型和Tent-SSA-BP的进化曲线图。从图中可以看到,使用Tent混沌映射产生大量的初始原子,从中选出适应度最佳的若干个原子作为初始种群,从而改进的SSA算法比改进前的SSA算法收敛速度加快。 图6 收敛曲线对比图 平均绝对误差百分比描述的是模型真实值和预测值之间的误差百分比,计算公式: (16) 表5 精度对比 4.2.2 算法对比 为了突出算法的优势,与其它算法优化结果进行对比,表6为对比结果。由表6可知,水分预测值的均方误差小于温度预测值,但是平均绝对误差百分比却大于温度,说明水分预测值比温度预测值离散程度更小,但是温度的预测比水分更精确;在水分的预测上,改进后的麻雀搜索算法的均方误差和平均绝对误差百分比都有明显减小,并且相比其它算法这2项数据都更小,所以精度更高;对于温度的预测,虽然对比遗传算法和粒子群算法提升效果并不明显,但是对比优化前,精度是有明显提升。 由于数据较多不方便观察,就选取部分数据作图进行对比,预测值和真实对比以及误差对比如图7、图8所示。从图中可以看出,对比其它方法,无论是在水分还是在温度方面,改进后的SSA-BP模型误差波动性更小更加接近期望值,性能更好。 图7 预测值和真实值对比 图8 误差对比 表6 不同优化方法的结果比较 本文针对烟叶复烤阶段工艺参数设置问题,分析了现阶段研究的情况与不足,提出了运用BP神经网络预测水分和温度为参数设置提供依据。运用麻雀搜索算法对BP神经网络的初始权值和阈值进行优化,提升了BP神经网络的性能;并引入了Tent混沌映射产生混沌序列,对麻雀搜索算法的初始种群位置进行了优化,对比算法改进前既能保持多样性,从而避免局部最优解,也能提高收敛速度和全局搜索能力。同时,还与遗传算法和粒子群算法优化效果进行了对比,结果显示所提算法的预测精度和稳定性都更好。综上所述,本文提出的基于Tent混沌映射改进的SSA-BP神经网络算法预测效果更好。3.2 改进策略
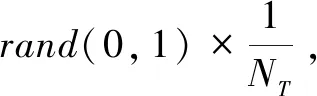
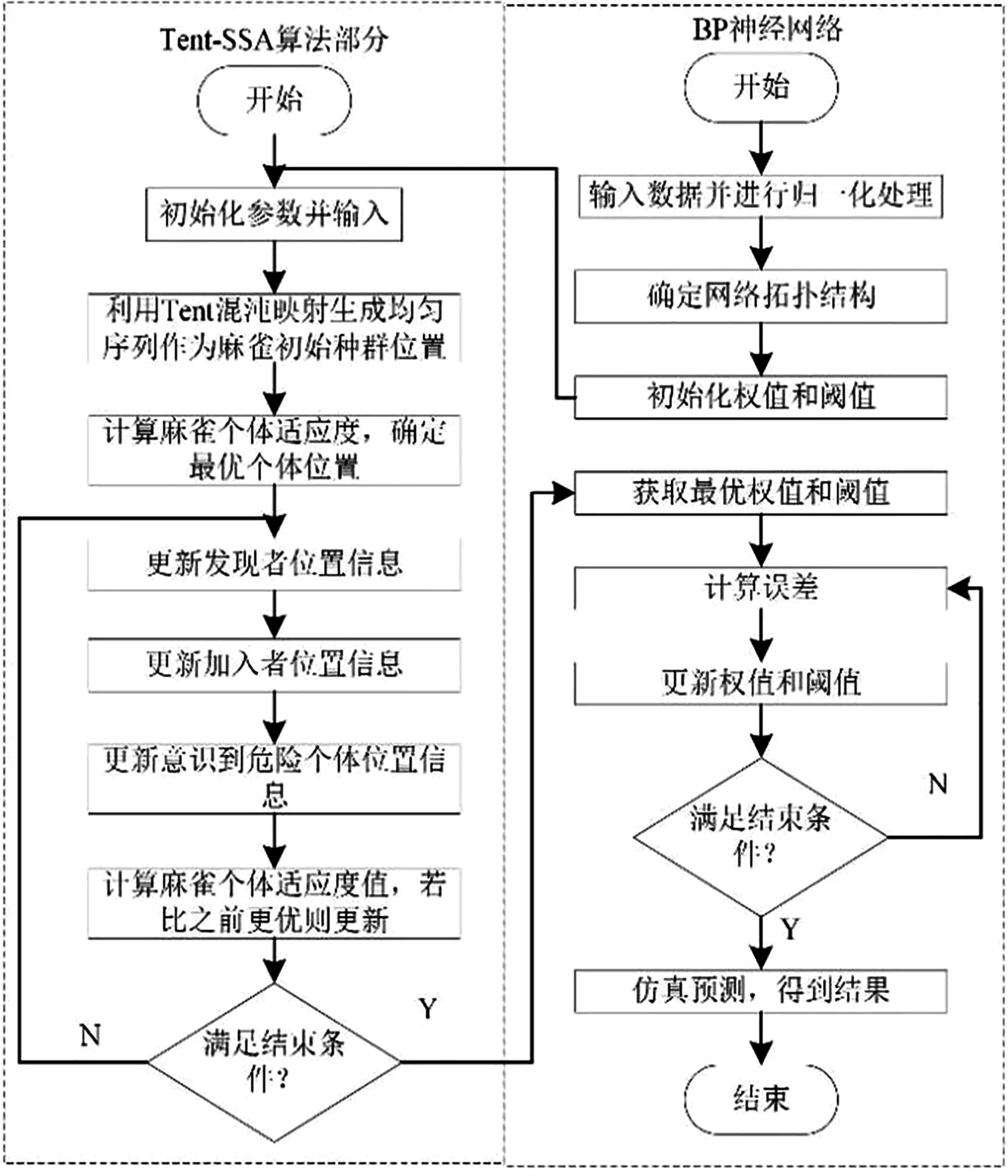
3.3 优化BP神经网络
4 结果分析与算法对比
4.1 模型参数选择
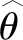


4.2 结果分析
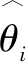

5 结论

