基于PF-GPR算法的锂离子电池剩余使用寿命预测

吴 菲，郑秀娟

(1.武汉科技大学冶金自动化与检测技术教育部工程研究中心，湖北 武汉，430081；2.武汉科技大学机器人与智能系统研究院，湖北 武汉，430081)

锂离子电池作为诸多领域储能系统的核心部件，具有输出电压高、能量密度大、循环性能好、自放电量小、无记忆效应以及环保等突出优点[1]。然而在实际应用中，锂离子电池性能会因其内部不可逆的物理、化学反应以及工况条件等因素而逐渐老化、衰退[2-4]，从而导致用电系统发生功能性失效或损坏，并有可能造成巨大经济损失。因此，对锂离子电池进行高效管理是保障用电设备安全运行的重要措施，也是当前能源领域的研究热点问题。

锂离子电池的性能退化是一个动态、时变的复杂非线性电化学过程，其性能状态指标主要有荷电状态(state of charge, SOC)、健康状态(state of health, SOH)和剩余使用寿命(remaining useful life, RUL)等[4-6]，可利用滤波模型、数据驱动或数据融合的方法等对这些性能指标进行估算[7-8]，其中，基于滤波模型的估算方法主要有扩展卡尔曼滤波(extended Kalman filter，EKF)[9-10]、无迹卡尔曼滤波(unscented Kalman filter，UKF)[2, 11-13]、粒子滤波(particle filter，PF)[14-16]等，该类方法将SOC、SOH和RUL等作为系统内部状态，通过建立系统状态空间方程再以递推的形式实现最优估计；利用数据驱动对锂离子电池性能进行估算的方法则从数据本身出发，借助神经网络(neural network,NN)[17-18]、支持向量机(support vector machine, SVM)或相关向量机(relevance vector machine,RVM)[7, 15, 19]等机器学习方法对历史数据进行学习和分析，从而提取电池的性能状态；数据融合法主要通过有效融合多种预测方法，综合利用单个方法的优点来改善模型的性能、提高整体模型的预测精度，从而提供更为可靠的估算和预测结果，如Chang等[7]提出了融合PF与RVM的锂离子电池寿命预测方法，并对预测结果的不确定性进行了分析，Li等[15]提出了一种融合交互式多模型PF与支持向量回归的方法，Ma等[16]在提出一种容量再生检测方法的基础上，融合自回归模型与PF算法对锂离子电池RUL进行了预测。不过，已有研究大多只关注了锂离子电池的全局退化趋势而忽视了其局部容量再生行为，即电池充放电结束后，在短期搁置时出现局部容量增加的现象，这将在一定程度上改变正常的电池容量退化曲线，进而影响电池RUL预测的准确性。有鉴于此，本文在综合考虑锂离子电池容量全局退化趋势和局部再生现象的基础上，建立一种新的电池容量退化模型，提出融合PF与高斯过程回归(Gaussian process regression，GPR)的锂离子电池RUL预测算法并对该算法的有效性进行验证。

1 锂离子电池容量退化过程建模

1.1 电池数据集

本文基于NASA Ames Prognostic Center of Excellence (PCoE)提供的电池数据集[20]，选取其中容量退化特征较明显的B5、B6、B7和B18电池为典型样本。该数据集是通过在室温下对18650号锂离子电池(额定容量2 Ah)进行循环充放电实验而获得的，电池充放电循环工况如下：

(1)充电测试：电池在1.5 A恒定电流模式下充电，直到电池电压达到4.2 V，然后以恒定电压模式继续充电，直到充电电流降至20 mA；

(2)放电测试：电池在2 A的恒定电流模式下放电，B5、B6、B7和B18电池的放电截止电压分别为2.7、2.5、2.2、2.5 V；

(3)通过电化学阻抗谱进行阻抗测量，扫描频率为0.1 Hz～5 kHz。

当电池容量衰减至额定容量的70%左右时停止实验，因此，实验中将电池容量失效阈值设置为1.38 Ah。图1所示为B5、B6、B7、B18电池的容量退化曲线。由图1可见，4组电池的容量衰减特征大致相似，前期退化速率较慢而后期退化速率明显加快，都出现了多次局部容量再生现象，并且每次容量再生的程度和时间也存在差异。4组电池中B6电池的容量衰退速度最快，B7电池的容量衰退速度最慢，后者容量在实验结束时仍未衰减至失效阈值。

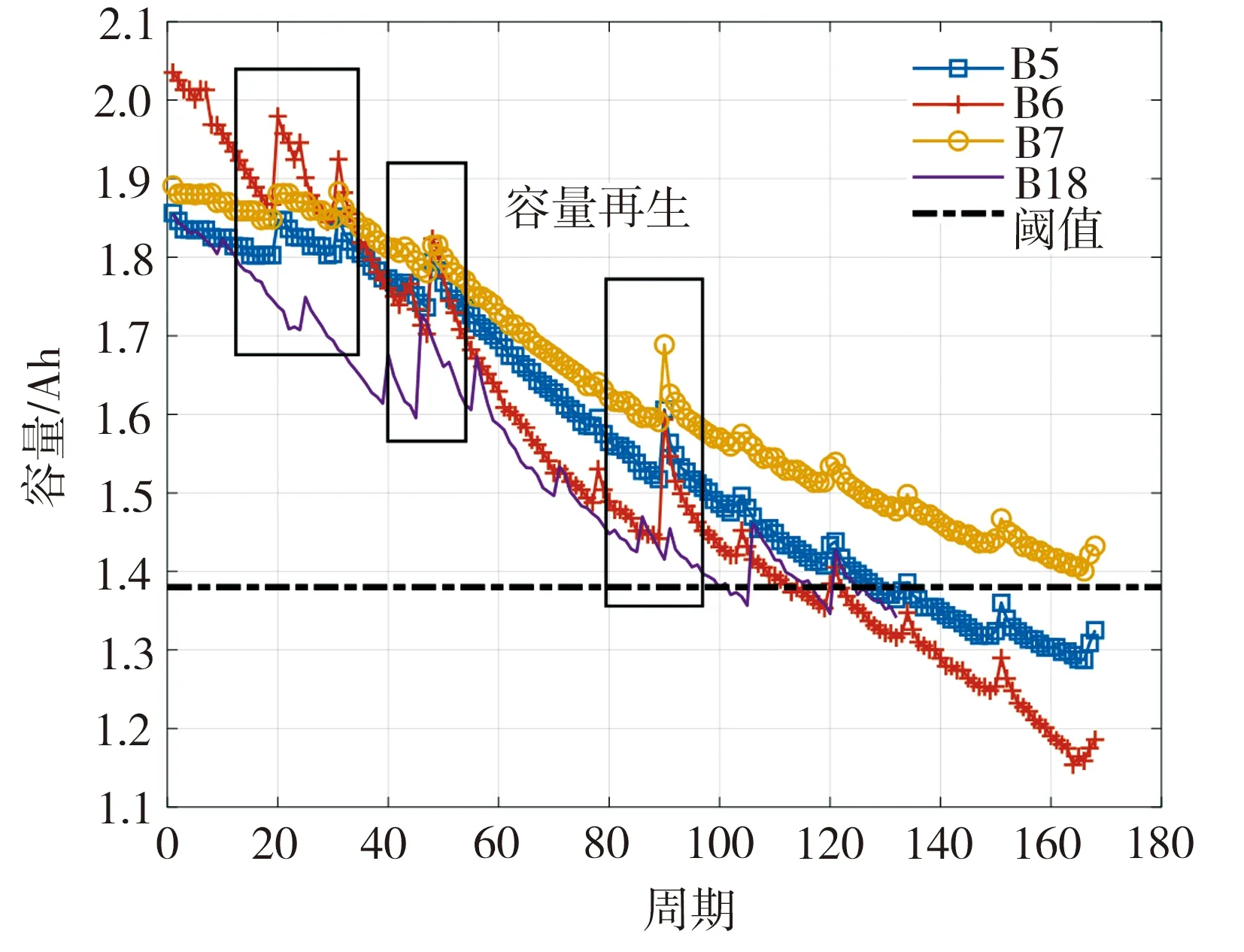
图1 B5，B6，B7和B18电池容量退化曲线

1.2 电池容量全局退化模型

用来描述锂离子电池容量退化过程的双指数经验模型[21]为：

xk=akexp(bkk)+ckexp(dkk)

(1)

式中，k为循环次数，xk为k次循环时的电池容量，a、b、c、d是根据电池历史数据拟合的参数。虽然该模型能较好地拟合锂离子电池容量的衰退趋势，但在后续电池RUL预测过程中需处理4个参数，计算复杂且误差较大，因此，Russell等[22]提出了一种改进的双参数模型：

(2)

式中，α是决定电池容量退化速率的参数，参数β与电池容量退化速率的峰值位置有关，vk、vα和vβ表示系统噪声。该模型只需处理2个参数，故而大大减少了计算工作量。

1.3 考虑局部再生的电池容量退化模型

文献[23]指出，当电池搁置时间不足2 h时对电池容量恢复几乎没有影响，超过10 h时电池容量恢复量则较为明显。以B5电池为例，提取出对应的搁置时间并去除异常点，得到电池搁置时间与其再生容量的拟合曲线如图2所示。基于该拟合曲线，建立锂电池容量局部再生模型为：

g(t)=a1ta2+a3

(3)

式中，g(t)表示电池容量的增量，t表示电池搁置的时间(h)，a1、a2、a3是需要拟合的参数。

综合锂离子电池容量的全局退化模型及局部再生模型，建立锂离子电池容量的退化模型为：

(4)

式中，γt∈{0,1}，是一个判断能否发生容量再生现象的二元变量，取值条件为：

(5)

式中，θ是一个超参数，它随历史数据集的变化而变化，根据实验数据，此处选取θ=10；Δt(k)表示电池第k次循环与第k-1次循环之间的间隔时间，T(k)是一个新电池完成第k次充放电循环的时间。

采用拟合优度R2和均方根误差(root mean squared error, RMSE)两个指标对模型进行评估，二者表达式为：

(6)

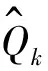
图2 B5电池搁置时间与容量再生量拟合曲线

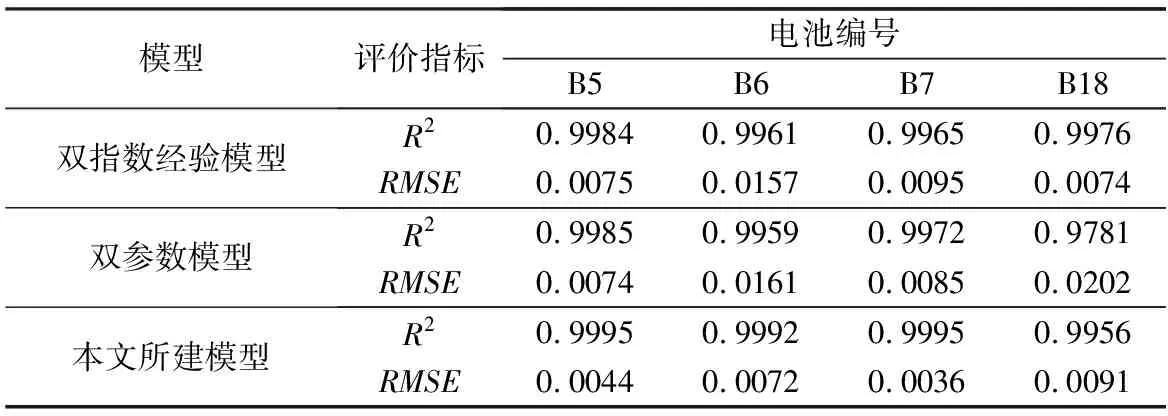
表1 锂离子电池容量退化模型评估

2 锂离子电池RUL预测

2.1 粒子滤波(PF)算法

PF算法基于贝叶斯滤波和蒙特卡罗算法，以样本均值代替积分运算获得状态的最小方差估计，通过状态更新和测量更新得到状态的概率密度分布函数(probability density function, PDF)。使用PF算法来估计本文所建锂离子电池退化模型(式(4))的参数，假设初始状态为x0，其PDF可以表示为p(x0|Q0)=p(x0)，则状态的一步预测可表示为：

p(xk|Q1:k-1)=

(7)

式中，Q1:k-1={Q1,Q2,…,Qk-1}表示第1个周期到第k-1个周期的电池容量。在k时刻获得测量值Qk，则更新后的状态后验PDF可表示为：

(8)

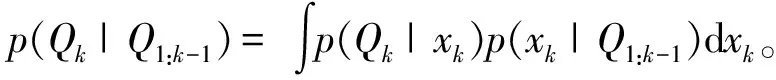
(9)

(10)

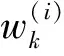
(11)

式中，π(·)表示重要抽样密度函数，一般选择为π(xk|xk-1)=p(xk|xk-1)。最后，在粒子权重更新过程中利用重采样算法，保留并复制权重大的粒子，淘汰权重小的粒子，从而减少粒子的退化。

需要指出的是，采用粒子滤波算法进行状态预测时，由于缺少预测起始时刻之后的测量值，将导致状态的后验PDF无法完成更新过程，只能利用所建系统模型迭代进行状态预测。随着预测步长的增加，迭代过程中的误差变得越来越大，从而可能导致预测结果不可信。

2.2 高斯过程回归(GPR)模型

数据驱动方法可借助机器学习建立电池电压、电流、温度和容量等数据和电池状态之间的非线性映射关系，其中高斯过程回归模型是一种非参数模型，能够输出预测均值、方差和置信区间，预测结果具备不确定性表达能力。给定一组输入和输出序列D={(xi,yi)},i=1,2，…,n,则GPR模型可以表示为：

y=f(x)+ε

(12)

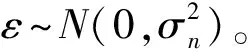
(13)

式中，Y={y1,y2,…,yn}，X={x1,x2,…,xn}，K(X,X)=[Kij]=[k(xi,xj)],为n×n阶对称正定协方差矩阵，用来描述xi与xj之间的相关性。I为n阶单位矩阵。Y和预测值Y′的联合先验分布为：

(14)

式中，X′为测试输入数据。预测值的集合Y′的后验分布为：

(15)

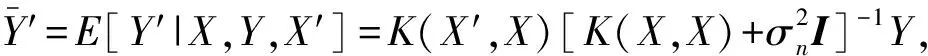
一般说来，使用电池容量数据{Qk}作为GPR模型训练的输入和输出数据时，预测过程需满足：

(16)

式中，L表示输入的维数，P表示预测的步长，且L=P。该处理方式存在两个不足：一方面，由于训练数据只包含单一的电池容量值，数据量有限；另一方面，锂离子电池容量难以直接在线获取，在实际应用中，无法通过直接测量容量来评估电池的状态。

通过对锂离子电池容量退化数据进行分析发现，在充电过程中，随着锂离子电池的老化，电压、电流和温度都存在着规律性的变化，以B5电池的电压、电流和温度分别在第10、50、100周期的变化为例(见图3)，可以看到随着电池的老化，相应充电电压升至截止电压所需时间以及充电电流保持恒定的时间均变短，电池温度更快速地升至最大值。根据这种变化趋势，可以利用GPR模型处理锂离子电池的电压、电流和温度与容量之间的映射关系，即：

(17)

然而，基于GPR的锂离子电池RUL预测方法只能为退化状态提供一个点估计，随着时间的推移，电池退化状态不断变化，单一退化模型不足以完整描述整个退化过程，特别是对于退化过程中的电池容量再生现象，利用GPR很难实现准确跟踪。

2.3 基于PF-GPR算法的锂离子电池RUL预测

针对单独使用PF或GPR算法在进行电池退化预测时存在的优点和不足，本研究提出PF-GPR融合算法对锂电池RUL进行预测。首先利用GPR模型预测得到锂离子电池全局退化趋势，从而在预测过程中实现对PF后验概率密度函数和模型参数的更新，使PF能够跟踪局部的容量再生现象，具体步骤如下：

Step1：从NASA PCoE电池数据集中提取电池充电状态下的电压、电流、温度作为输入特征，提取电池容量作为输出特征。将数据进行预处理，剔除异常数据点并进行数据的归一化处理，然后将数据集按7∶3划分为训练集和验证集；

Step2：利用Step1中确定的训练集训练得到GPR模型；

Step3：假设预测起始时刻为T，利用GPR预测模型输入测试集特征预测得到T时刻后的测试集容量{QT,QT+1,…,QT+n}；

Step4：利用电池容量局部再生模型(式(3))得到预测值，再以Step3中的高斯预测值{QT,QT+1,…,QT+n}充当观测值来修正PF算法，进行状态更新过程；

Step5：如果预测容量达到给定的阈值QEOL，则锂离子电池RUL=tEOL-tT。

该融合算法主要流程如图4所示：

图4 PF-GPR算法流程图

3 仿真实验

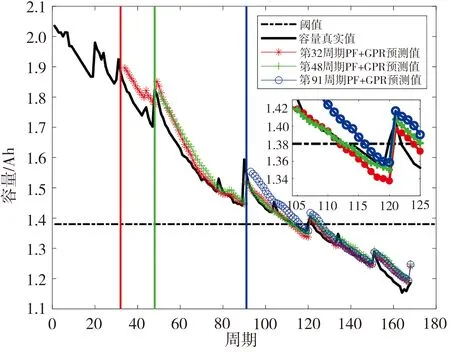
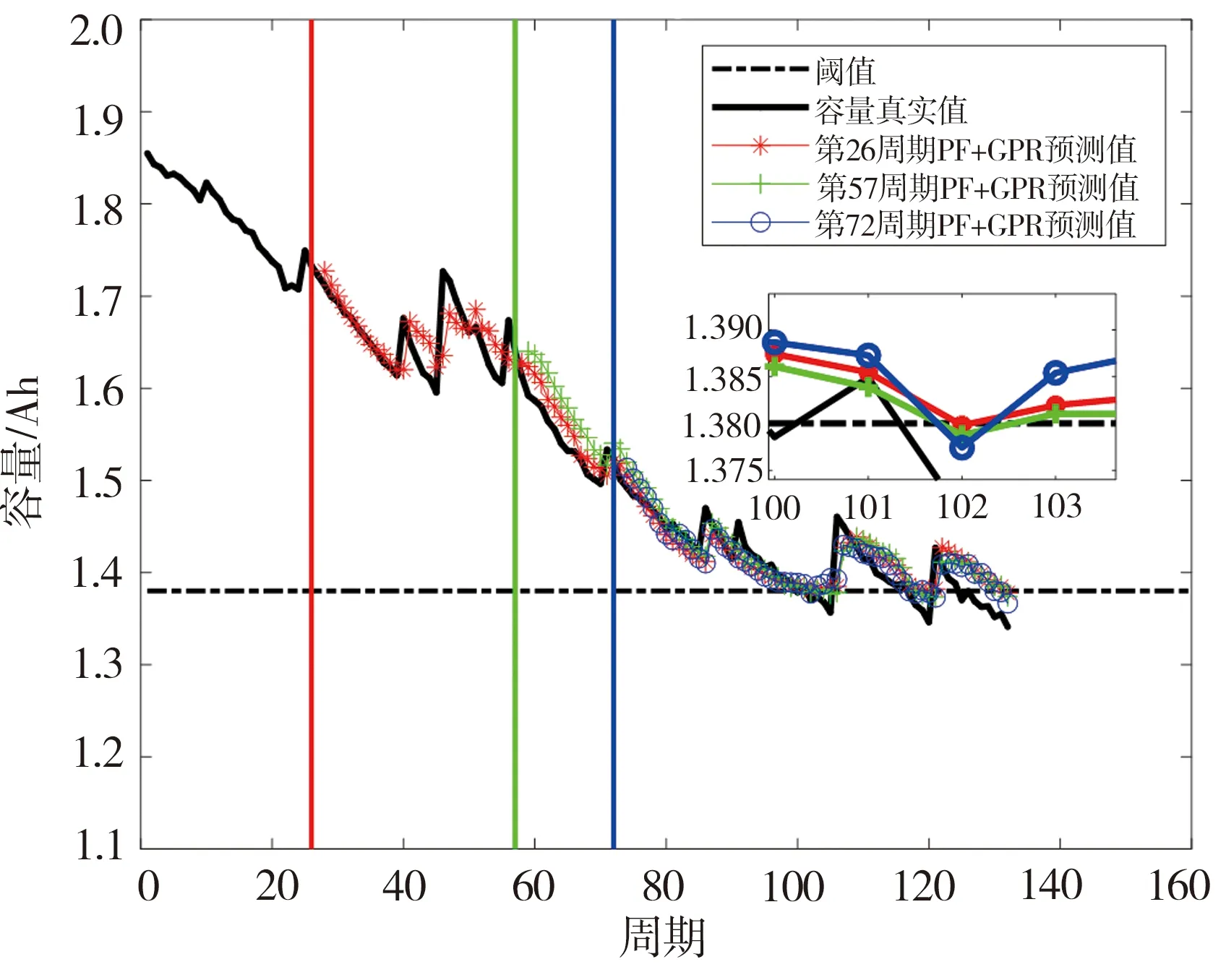
因NASA PCoE电池数据集中的B7电池在实验结束时仍未衰减至失效阈值，故此处选用B5、B6、B18电池进行仿真实验来验证本文所提算法的有效性，B5、B6、B18电池的实际寿命结束周期(end of life, EOL)分别为128、112和99。由图1所示的电池容量的退化曲线可知，B5电池容量局部再生现象出现在第32、90和121周期；B6电池相应现象出现在第32、48和91周期；B18电池相应现象则出现在第26、57和72周期，选取这些容量再生点作为预测起始时刻，使用本文提出的PF-GPR模型进行仿真实验。设置粒子数M为500，预测开始时，初始参数(x,α,β)的值根据T时刻之前数据利用PF估计得到。假设系统的噪声都是高斯白噪声，设置状态噪声方差为:v=vα=vβ=10-4，系统测量噪声方差为w=5×10-5。实验结果见图5，相应的预测结果评价分别列于表2～表4，其中Erul为电池RUL的预测误差，表达式为：

Erul=|RULT-RULP|

(18)

式中，RULT表示预测起始时刻T处的剩余使用寿命值，RULP表示预测值。由表2～表4中电池RUL预测结果的评价指标可以看出，本文所提融合方法总体预测误差较小，整体预测精度高，对于电池容量再生现象也有较好的预测效果，并且将预测点设置为电池寿命早期条件下的RUL预测精度最高。同时也注意到，B5电池以121周期为预测起点时，相对误差较大，主要原因应为预测起始点与电池EOL接近。

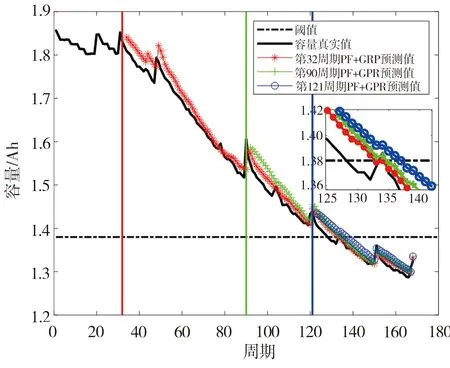
(a) B5电池

(b) B6电池

(c) B18电池

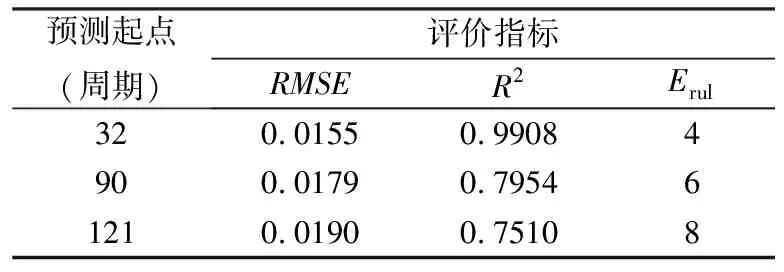
表2 B5电池预测结果评价

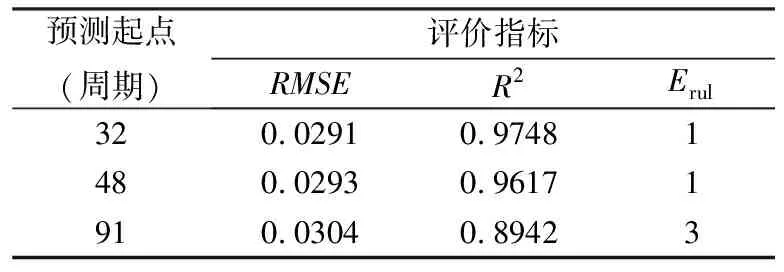
表3 B6电池预测结果评价

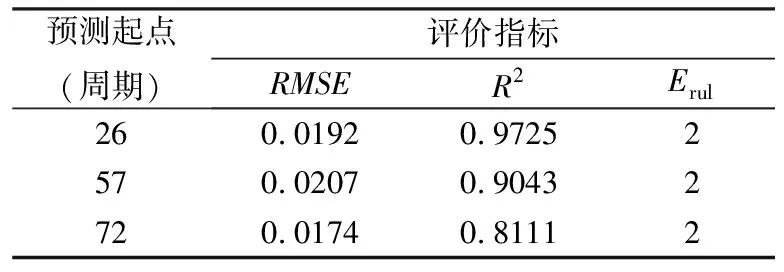
表4 B18电池预测结果评价

设定预测起始点为第30周期，分别利用PF、GPR以及本文所提PF-GPR融合算法对锂离子电池RUL进行预测，相关性分析仿真结果如图6所示，相应的预测结果对比见表5。由图6可见，本文所提PF-GPR融合算法相较于GPR算法的预测结果更接近于真实值，表5预测结果对比分析显示，相较于GPR算法，PF-GPR融合算法在维持锂离子电池RUL预测精度基础上提高了整体预测效果，验证了本文所提融合算法的有效性。

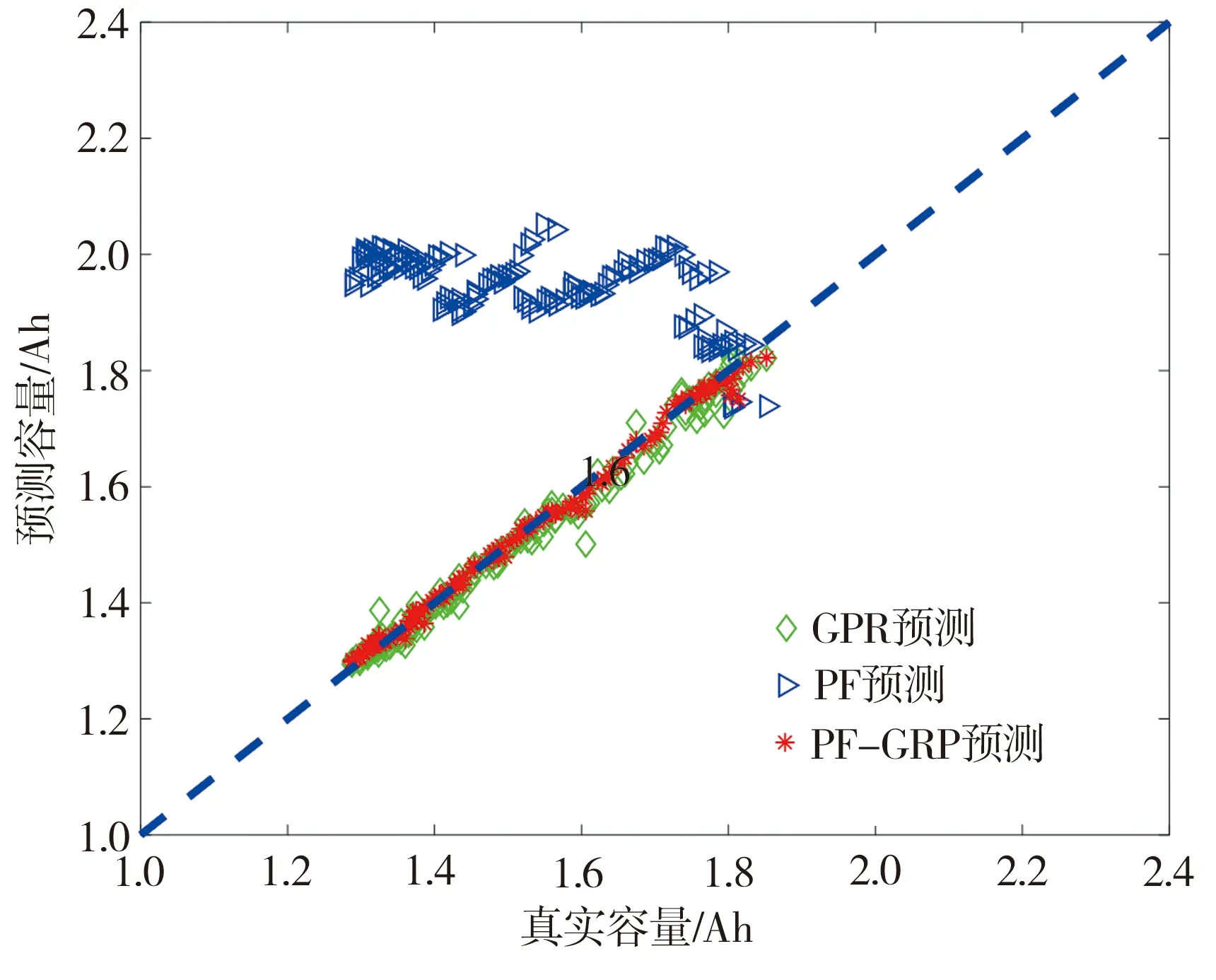
(a) B5电池

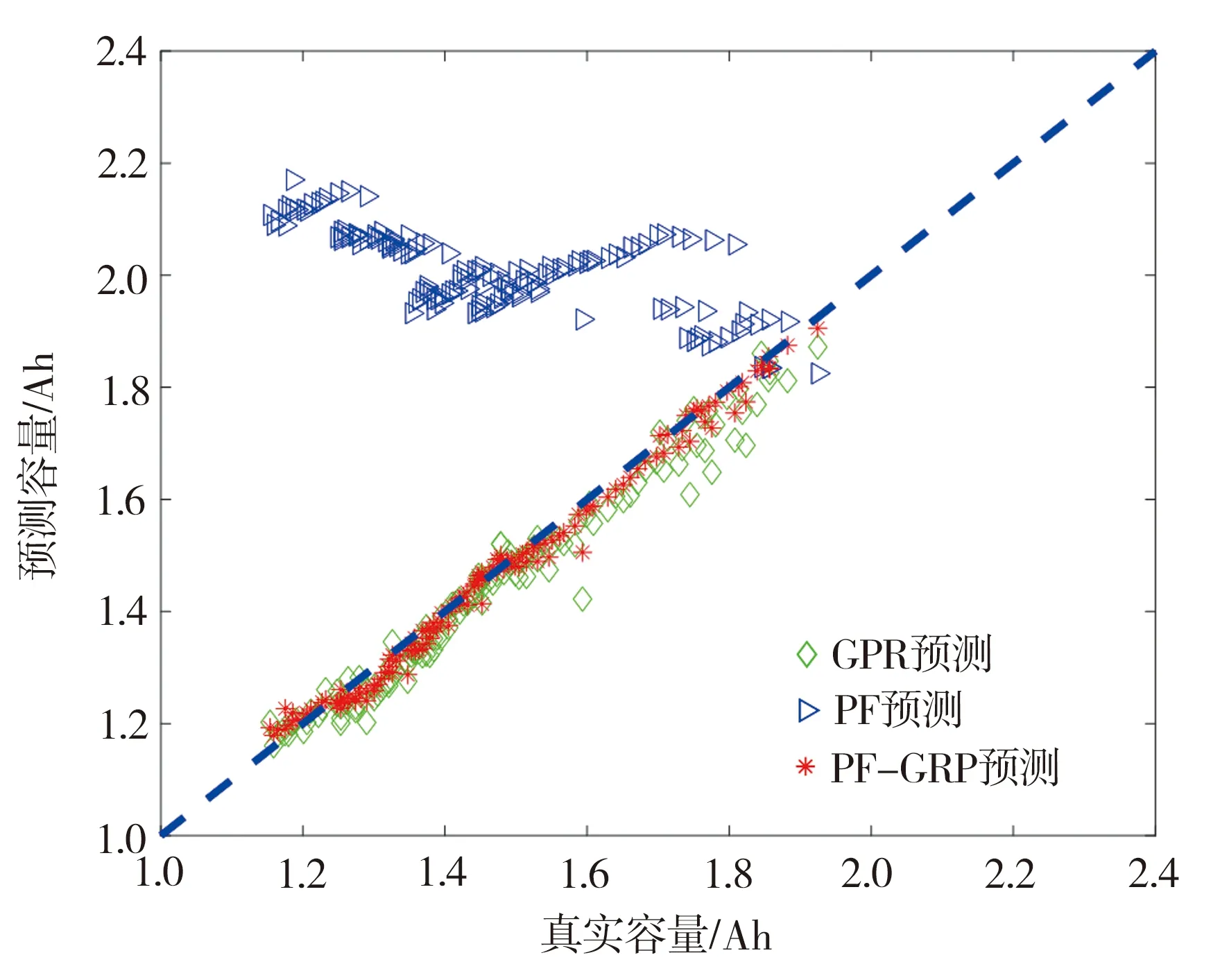
(b) B6电池

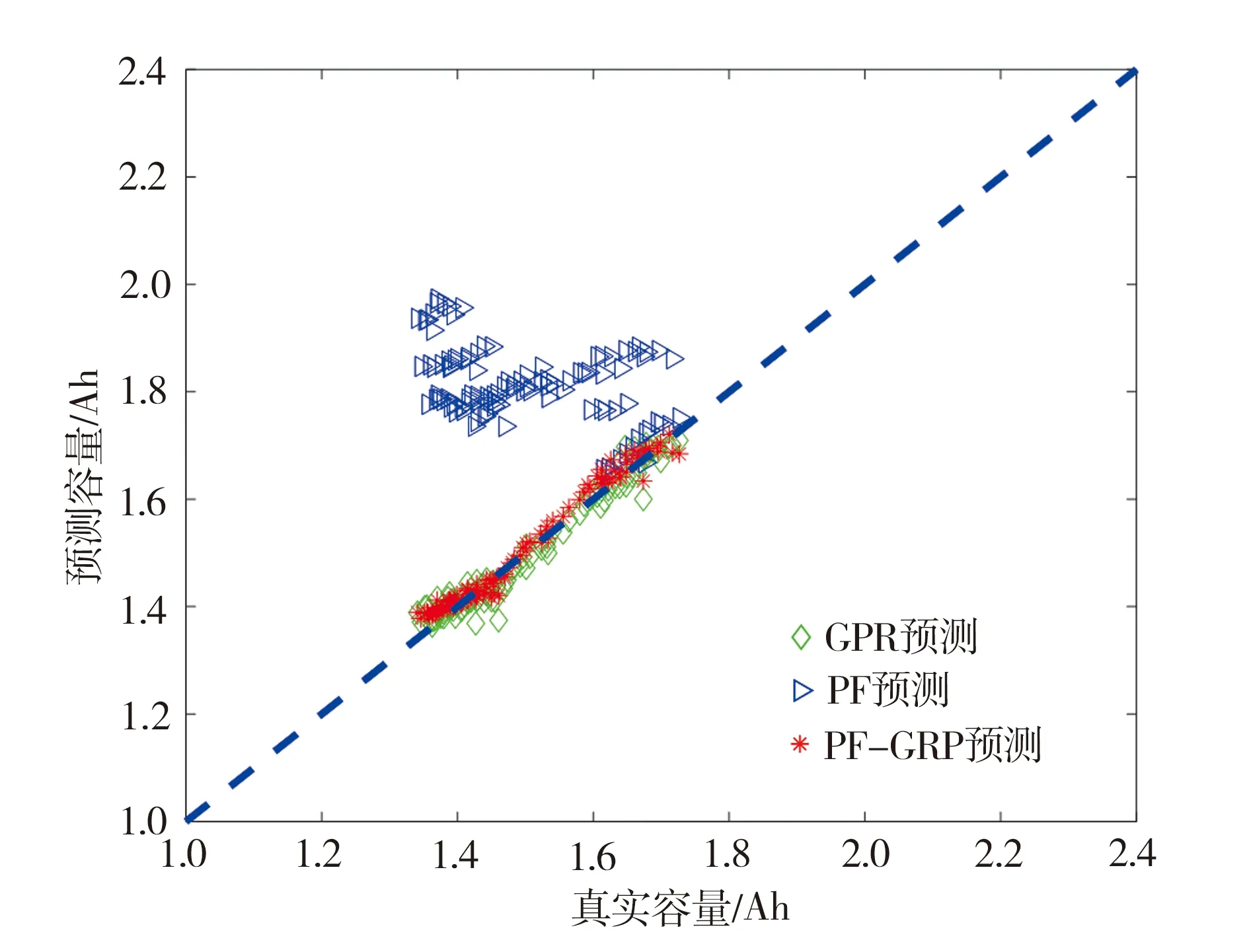
(c) B18电池

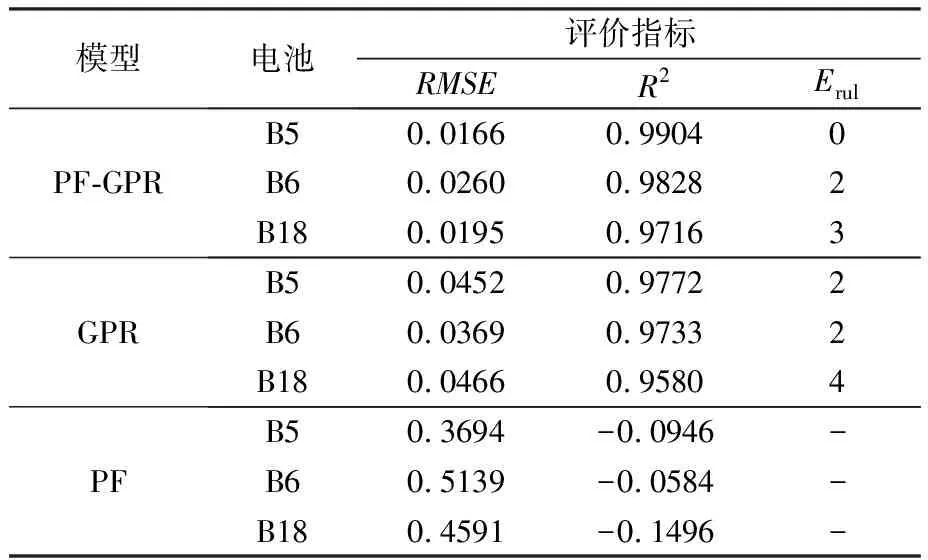
表5 预测结果对比

4 结语

针对锂离子电池在退化过程中出现的容量再生现象，建立了电池局部容量再生模型，并提出了基于PF-GPR算法的锂离子电池RUL预测方法，该方法主要利用GPR模型学习电池充电过程中所采集电压、电流和温度数据与电池容量之间的非线性映射关系，并对电池容量退化的全局趋势进行预测，从而在预测过程中实现对PF的后验概率密度函数和模型参数的更新，使得PF能够跟踪局部的容量再生现象。借助NASA Ames Prognostic Center of Excellence (PCoE)提供的电池数据集进行的仿真实验表明，本文所提基于PF-GPR算法的锂离子电池RUL预测方法具有较高的预测精度，其有效性得到验证。