基于拉普拉斯特征映射的三维结构模态分析

符伟华，王 成，2+，陈建伟，赖雄鸣，李海波,2

(1.华侨大学 计算机科学与技术学院，福建 厦门 361021；2.厦门市企业互操作与商务智能工程技术研究中心，福建 厦门 361021；3.圣地亚哥州立大学 数学与统计学院，圣地亚哥 加州 92182，美国；

0 引言

模态是结构本身具有的振动特性，通过工作模态分析(Operational Modal Analysis, OMA)方法识别每阶模态的参数(如模态固有频率、振型、阻尼比等)，可以了解结构的动力学特性，进而进行结构的损伤识别[1]、结构优化[2]等。然而，对于许多大型复杂结构，可以利用的激励方式只有工作状态下的环境激励，从而导致无法对激励输入进行测量。为了解决该难题，一种仅通过利用结构的输出响应识别结构模态参数的方法引起了许多研究者的关注[3]。

当前，工作模态分析已经得到了广泛应用，各类工作模态识别方法层出不穷。PONCELET等[4]采用了独立分量分析和二阶盲辨识两种盲源分离技术，进行了纯输出模态分析。王成等[5]利用了主成分分析(Principal Component Analysis, PCA)进行模态参数识别,解决其他方法识别过程中出现虚假模态的问题。DEVRIENDT等[6]提出的基于传递率测量的OMA技术，用于降低由于谐波存在而导致模态参数识别错误的风险。

这些模态识别方法都取得了很好的实验效果，但对复杂三维连续体结构工作模态参数识别的研究甚少。白俊卿等[7]利用局部线性嵌入的流形学习方法，将模态数据集视作高维数据，通过寻找低维的线性嵌入，从而识别复杂三维连续体结构工作模态参数。王成等[8]利用模态坐标的概念，找出动力机械系统的振动模态振型与线性混合矩阵之间、模态响应与主成分之间的一一对应关系，提出一种新的三维结构时域统计模态分析方法。通过最小二乘反迭代，王建英[9-10]提出了二阶盲辨识的三维连续体结构工作模态参数识别方法。通过振动响应三维矩阵的直接组装，张天舒[11-12]提出了主元抽取的三维连续体结构工作模态参数识别方法。

近年来，流形学习在图像处理等多个工程领域得到了广泛应用。流形是一个几何概念，它表示镶嵌在高维空间中的低维几何结构[13]。基于这个概念，流形学习的降维过程中需保持降维之后的数据同样满足与高维空间流形有关的几何约束关系。目前，流形学习[14]运用较为广泛的算法有等距离映射(Isometric feature mapping, Isomap)[15-16]、局部线性嵌入算法[17]等。拉普拉斯特征映射(Laplacian Eigenmaps, LE)[18]是流形学习的主要算法之一，其基本思想是从局部角度构建数据之间的联系，使得相互间有联系的点在完成降维后尽量保持该联系，这使得降维后的数据集依然能保持原来数据集的数据结构。相比主成分分析，LE能考虑数据的内在几何；相比等距离映射，拉普拉斯特征能仅从局部构建数据的内在几何，使得算法时间复杂度更低[19]。本文的主要创新点如下：

(1)统一提出了基于流形学习的工作模态参数识别方法体系。其基本思想是找出各阶模态坐标响应与低维嵌入数据之间的一一对应关系，从而将工作模态参数识别问题转化为结构振动响应数据的流形降维问题。

(2)将LE算法引入动力学系统，提出基于LE的工作模态参数识别方法，并与主成分分析、等距离映射进行理论比较。

(3)结合最小二乘广义逆反迭代或者直接组装三维位移响应求解法，提出了基于拉普拉斯特征映射的复杂三维结构工作模态参数识别方法。

(4)在三维圆柱壳结构上的振动响应仿真数据集上进行基于LE的三维结构工作模态参数识别方法的效果验证。

1 基于LE的复杂三维连续体结构模态参数识别

1.1 工作模态参数识别问题的描述

工程结构系统一般可看作是一个具有一定粘性比例阻尼的系统。结合结构的动力学理论，对于包含n个自由度的线性时不变振动系统，该系统在物理坐标系统中的动力学方程表示如下：

(1)

式中：M∈n×n，为结构系统的质量矩阵;C∈n×n,为结构系统的阻尼矩阵;K∈n×n,为结构系统的刚度矩阵；n×T与n×T，依次为结构系统的位移响应信号、速度响应信号与加速度响应信号的时域采样矩阵；F(t)∈n×T,为系统的外载荷激励向量的时域采样矩阵。

针对阻尼较小的n自由度工程结构，结构的位移响应信号X(t)=[x1(t),x2(t),…,xn(t)]T∈n×T,在模态坐标中可表示如下：

(2)

式中:矩阵Φ=[φ1,φ2,…,φn]∈n×n,为由结构的n阶模态的振型向量φi(i=1,2,…,n)所构成的模态振型矩阵；Q(t)=[q1(t),q2(t),…,qn(t)]T∈n×T,为由结构的n阶模态响应qi(t)∈1×T(i=1,2…,n)所组成的模态响应矩阵。且式(2)中的主振型向量φi需要满足相互正交，即

(3)

其中mi为第i阶模态质量。并且，qi(t)与qj(t)二者相互独立，其中i与j为不同的模态阶数。

工模模态识别方法的基本思想是通过仅有结构输出的位移响应信号X(t)，识别出结构的各阶模态振型Φ和模态响应Q(t)；最后用单自由度识别技术识别出各阶的模态固有频率f以及模态阻尼比ξ。

1.2 基于LE算法的工作模态参数识别

拉普拉斯特征映射算法是流形学习的热门算法之一，它的基本思想是从局部的角度去构建数据之间的联系，这使得降维后的数据集依然能保持原来数据集的内部结构。LE算法的具体描述如下。

(4)

通过推导式(4)，可得到变换后的LE目标优化函数如下：

mintrace(STLS),

s.t.

STDS=I。

(5)

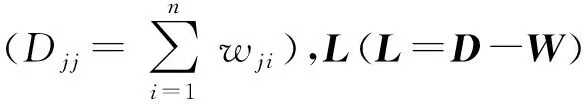
LS=-DSΛdiag。

(6)

式中：Λdiag为一个对角矩阵，由于D，L均是实对称矩阵，故它们的转置与自身相等。因此，对于单独的si(t)向量，式(6)可写成以下形式：

Lsi(t)=λDsi(t)。

(7)

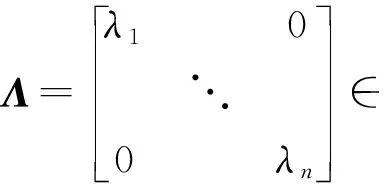
LE通过对式(7)做特征值分解，并将其d(d≪n)个最小非零特征值[λ1,λ2,…,λi,…,λd]所对应的特征向量{υ1，υ2，…，υi，…，υd}作为降维后的结果输出，即可达到降维的目的。n个d维向量S(t)={s1(t),s2(t),…,sd(t)}T∈d×T与降维后的结果{υ1，υ2，…，υi，…，υd}一致。

因此，依据最小二乘广义逆，存在变换矩阵B=(b1,b2,…,bd)∈n×d，使得式(8)成立，X(t)可分解为式(9)。

B=X(t)ST(t)(S(t)ST(t))-1,

(8)

(9)

1.3 基于LE的三维结构工作模态参数识别的物理意义

当使用拉普拉斯特征映射获取T个S维向量构成的S(t)={s1(t),s2(t),…,sd(t)}T∈d×T(向量si(t)与sj(t)之间满足相互正交(i≠j))时，由式(2)、式(3)和式(9)，发现各阶模态响应矩阵Q(t)对应LE得到的低维嵌入S(t)={s1(t),s2(t),…,sd(t)}T∈d×T。模态振型Φ对应变换矩阵B=(b1,b2,…,bd)∈n×d。因此，模态参数识别可通过运用LE分解求得。具体的求解流程如图1所示。图1中的流形学习方法可以是线性的主成分分析(PCA)[8]、也可以是非线性的等距离映射(Isomap)[16]。

1.4 基于LE的三维结构工作模态参数识别方法

1.4.1 运用最小二乘广义逆反迭代求解法

针对复杂的三维结构，本文将结构的时域响应信号表示如下：

(10)

在有限元的实验设计中，复杂三维连续体结构被离散化为H个检测点，时间的采样点总数为T个。因此，被离散化后的三维连续结构在时域上的响应在理论上可以近似用式(11)表示。

(11)

式中：S为有限元计算过程中的模态截断数，A(t)S×T为三维系统结构的模态响应矩阵。LE算法运用最小二乘法广义逆反代法做三维结构模态参数识别的流程图如图2所示。

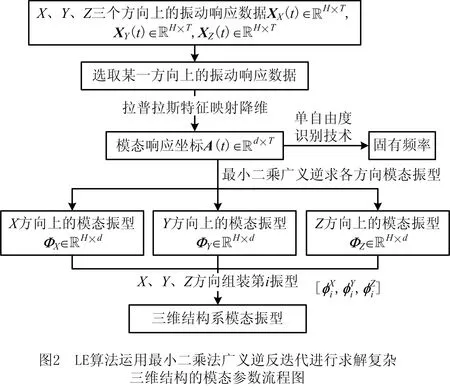
(1)在复杂三维结构的X，Y，Z轴3个方向上的时域数据集(XX)H×T(t)，(XY)H×T(t)，(XZ)H×T(t)中选取响应最大的那个方向上的振动数据作为识别的基础数据集。将选取的数据集记为E,则数据集E的维数为H,样本点数为T。

(2)利用LE算法计算数据集E降至d维空间上的低维嵌入数据A(t)d×T={a1(t),a2(t),…,ai(t),…,ad(t)}T，其中，t=1,2,3,…,T。

(3)用A(t)d×T替代式(11)中的A(t)S×T，用(ΦX)H×d替代式(11)中的(ΦX)H×S，用(ΦY)H×d替代式(11)中的(ΦY)H×S，用(ΦZ)H×d替代式(11)中的(ΦZ)H×S，通过该替换，式(11)可用式(12)表示。

(12)

(4)将步骤(2)中求得的A(t)d×T带入式(12)中，可依次求出(ΦX)H×d，(ΦY)H×d，(ΦZ)H×d，如式(13)所示:

(13)

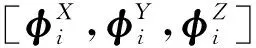
1.4.2 直接组装三维位移响应求解法

最小二乘法广义逆反代求解法在求解过程中，需要多次求解广义逆，使得求解精度出现下降，因此本文采用直接组装三维位移响应求解法。

根据式(2)，该方法将X，Y，Z三个方向的模态响应组装成整个三维结构的整体位移模态响应。组装后的公式如式(14)：

(14)

式中:(HThree)3H×T(t)为整个三维结构的整体模态响应；(XX)H×T(t)，(XY)H×T(t)，(XZ)H×T(t)分别对应X，Y，Z方向的位移响应信号；矩阵Φ3H×S是复杂三维结构的各阶模态主振型向量φi所构成的模态振型矩阵；QS×T(t)则是结构的各阶模态响应qi(t)所构成的模态响应矩阵，S是有限元计算过程中的模态截断数。

LE算法运用直接组装三维位移响应法做三维结构模态参数识别的流程图如图3所示。

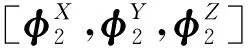
1.5 基于LE的三维结构工作模态参数识别与其他方法的比较

本文主要将基于LE的三维结构工作模态参数识别方法与基于主成分分析(PCA)[8]、等距离映射算法(Isomap)[16]的三维结构工作模态参数识别方法进行比较。正常情况下，算法的时间开销是不可忽视的问题。除此之外，复杂的三维结构具有一定粘性比例阻尼，因此采集到的数据集带有一些非线性特征。PCA算法是一种线性降维算法，当某阶模态非线性特征过多时，识别复杂三维结构的模态参数精度会变得不太理想。LE是一种非线性降维算法，在降维过程中，LE算法能更好地保留数据集的特征，从而处理数据的非线性特征。因此，LE算法在对复杂三维结构做模态分析时，某阶模态的识别精度在一定程度上能更优于PCA算法。Isomap算法也是非线性降维方法，与LE算法保留局部性质相比，Isomap算法是一种保留全局性质的算法，故这是Isomap时间开销高的主要原因。在识别精度方面，由于Isomap算法对数据的局部结构更为敏感，这会使得其在识别复杂三维结构模态参数时，对数据的要求更为严格，从而造成Isomap的识别精度在一定程度上会低于LE算法。3种方法的优缺点说明如表1所示。

表1 基于LE与PCA和Isomap的三维结构工作模态参数识别比较

2 仿真验证结果与分析

2.1 实验对象和仿真数据介绍

为了验证LE算法能有效识别三维连续体结构系统的模态参数，进行实验仿真验证。仿真验证中主要进行具有复杂三维结构的圆柱壳系统[20-21]研究，模拟图如图4所示。

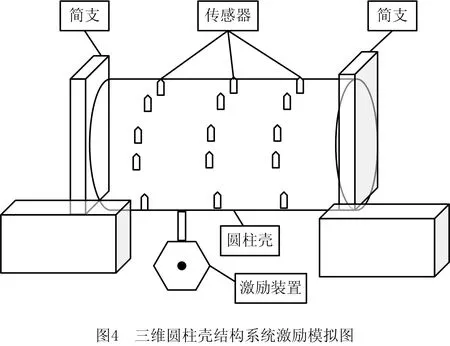
圆柱壳系统有两端简支，在其表面放置一定数量的振动信号传感器，然后利用设备记录传感器X、Y、Z三个方向上的振动响应信号。圆柱壳的参数设计如下：圆柱壳使用的材料厚度为0.005 m，半径长度是0.182 5 m，总长0.37 m，同时圆柱壳材料的弹性模量为205 Gpa[8]，泊松比的数值是0.3，密度是7 850 kg/m3。在进行实验仿真的过程中，人为地设置阻尼比η为0.03，进行测量。

圆柱壳上的传感器观测点布置规则如下：首先沿着圆柱壳的长度轴向均匀分成38个圈，然后在每个圈中均匀地布置115个观测点，因此圆柱壳表面共布置H=38×115=4 370个传感器观测点。在布置好装置，通过使用激励装置对圆柱壳施加高斯白噪声激励的基础上，再采样得到三维圆柱壳的振动响应信号。其中，将机器的采样频率设置成5 120 Hz，采样的时间长度设置成1 s，即T=5 120。

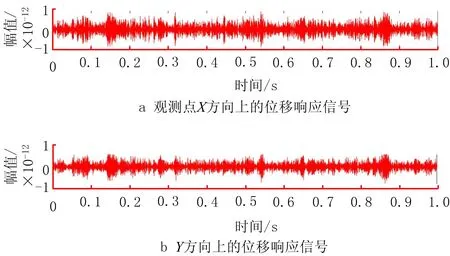
振动信号记录设备采用一套数采前端LMS SCADS-X Ⅲ，Test lab 9B系统，DELL M65。然后使用LMS Virtual.lab中的有限元方法对传感器输出的振动响应信号进行读取。从而测量到三维圆柱壳结构X、Y、Z三个方向的响应数据集合，第358个观测点的响应信号集合如图5所示。

2.2 评价指标

为了评价LE算法对三维圆柱体结构系统做模态参数识别是否具有有效性，本文将用LE算法识别到复杂三维结构的模态参数与利用有限元方法分析识别到的真实模态参数进行比较，分析LE算法识别的模态参数的有效性。

本文将使用模态置信度准则(Cmac)来评估LE算法识别到的模态振型准确度，

(15)

式中:φi为LE算法识别得到复杂三维结构的第i阶模态振型，ψi为利用有限元分析识别复杂三维结构得到的第i阶真实模态振型。由式(15)可知，模态置信度准则的取值范围0≤Cmac,i≤1，当Cmac,i的值越接近1时，所识别的第i阶的模态振型精度越高。

2.3 基于LE的三维圆柱体模态参数识别结果

本文采用1.4.2节的直接组装法识别三维圆柱体的模态参数，因为该方法相对最小二乘法广义逆反代法，对测量数据的噪声不敏感。当圆柱壳阻尼比η=0.03时，为了更直观地比较，本文将得到的三维模态振型图形进行旋转，得到各阶模态振型的二维形状图。本文将识别的模态振型与有限元分析的真实模态振型进行比较。有限元分析的真实模态振型如图6所示。

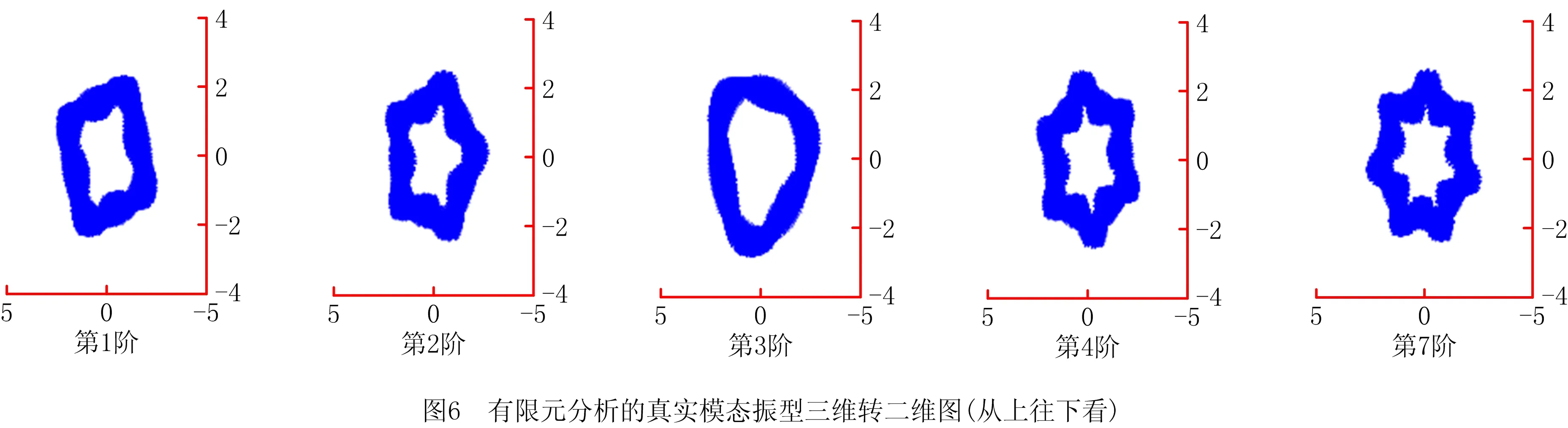
图7是基于LE算法识别的模态振型三维旋转成二维图。LE算法对三维圆柱壳参数识别出来的固有频率图如图8所示。然后用LE算法识别出的固有频率与有限元分析计算得到的真实固有频率进行比较，比较结果如表2所示。最后，根据模态置信度准则，求得LE算法的Cmac值，结果如表3所示。

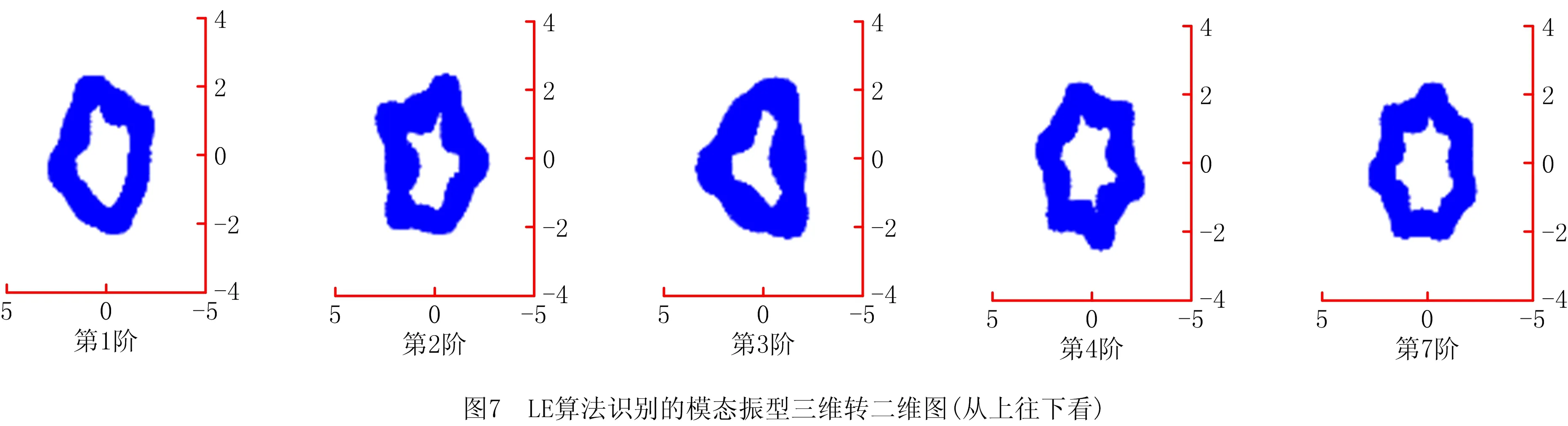
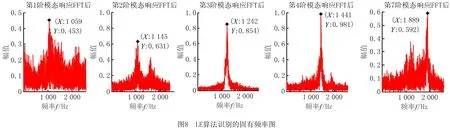
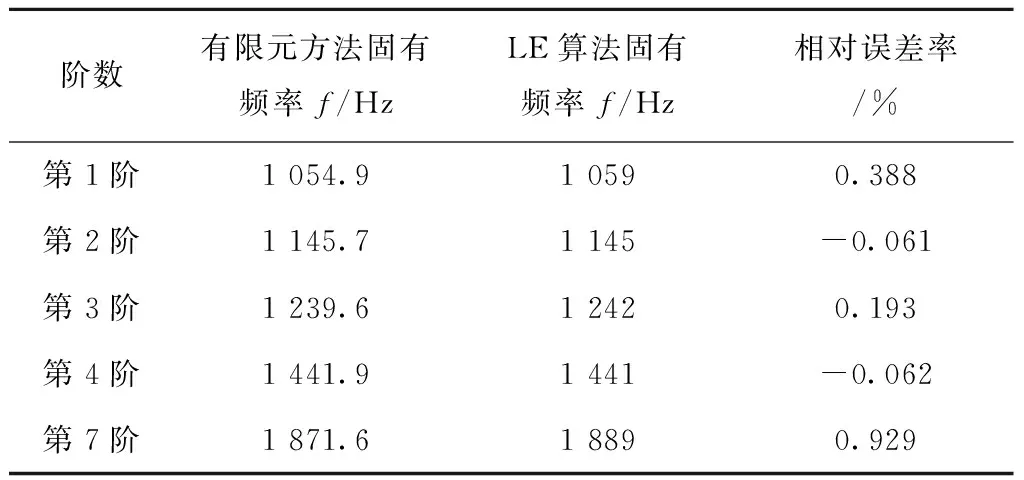
表2 有限元方法与LE算法固有频率相比较

表3 LE算法置信度准则值

2.4 基于LE的三维圆柱体工作模态参数识别结果分析

在1.5节中，本文采用PCA算法，Isomap算法与LE算法进行了比较，分析了他们各自的优缺点。表4和表5给出了利用PCA算法、Isomap算法与LE算法对三维结构模态参数识别的比较结果。

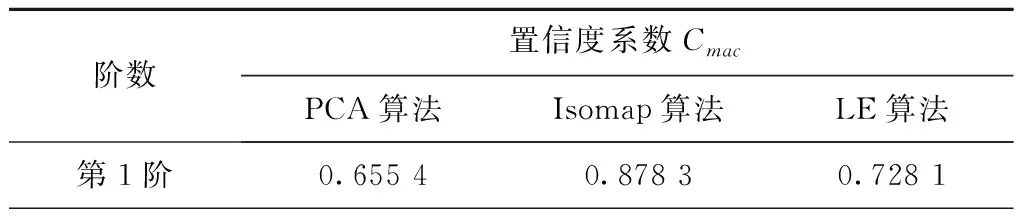
表4 PCA算法、Isomap算法与LE算法模态置信度系数比较

续表4

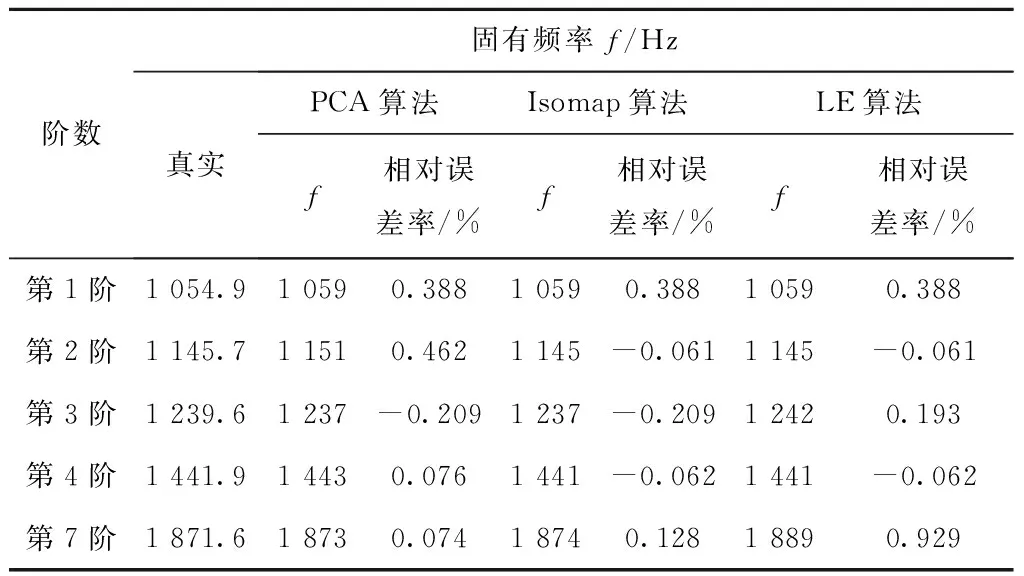
表5 PCA算法、Isomap算法与LE算法固有频率比较

通过表4可知，与PCA算法相比，LE算法第1、2阶的模态振型识别精度比PCA高，第3、4阶差别不大，第7阶的识别精度低于PCA。与Isomap算法相比，LE算法除了第1阶低于Isomap算法，第2、3、4和7阶的识别效果均比Isomap算法好。通过表5可知，LE算法识别第2、3、4阶的固有频率误差比PCA算法低，第7阶固有频率误差高于PCA算法。与Isomap算法相比，LE算法识别第3阶固有频率误差更低，但第7阶固有频率误差更高。

表6给出了PCA算法、Isomap算法与LE算法的时间开销，从表6可知，Isomap算法的时间开销远高于LE算法，LE算法的时间开销高于PCA算法。

表6 PCA算法、Isomap算法与LE算法时间开销比较

3 结束语

本文将拉普拉斯特征映射(LE)算法应用于三维连续圆柱壳结构系统的模态参数识别。通过在圆柱壳结构系统数据集上的仿真结果说明，LE算法能有效地识别三维结构系统的工作模态参数(模态振型、模态响应与固有频率)。LE算法的识别结果与PCA算法和Isomap算法相比，LE算法能更为均匀地识别出各阶模态振型；且与Isomap相比，LE算法识别速度更快，平均识别精度更高。

但是，LE算法在识别过程中，容易出现某阶的模态缺失或重叠现象。如何解决模态的缺失或重叠问题，是LE算法模态参数识别需要继续进一步解决的问题。除此之外，未来的工作中还可以用实际结构进一步验证该算法的有效性。