风筝飞行的动力学分析和实际应用

于冰川，杨 薇

(沈阳师范大学，沈阳 110034)

本文为中国高等教育学会2020年“基于一流课程建设的”教学改革与实践研究专项课题、中国教育学会2021年度规划课题(编号202100150702B)、国家教育考试科研规划2021年度重点课题(编号GJK2021004)阶段性成果。

将放风筝分为两个阶段，即放飞、抬升和高空稳定，进行抽象建模，利用动力学分析方程探究放飞过程的最优方式、抬升和高空稳定阶段的稳定原理，通过理论结果，定性分析市面上几种风筝的平衡原理、优势与不足，为风筝的优质化生产提供建议。

1 风筝起飞的动力学分析与最优放飞方式

在起飞阶段，将迎风面抽象为一个平面，对其运动学受力进行如图1方式的建模。

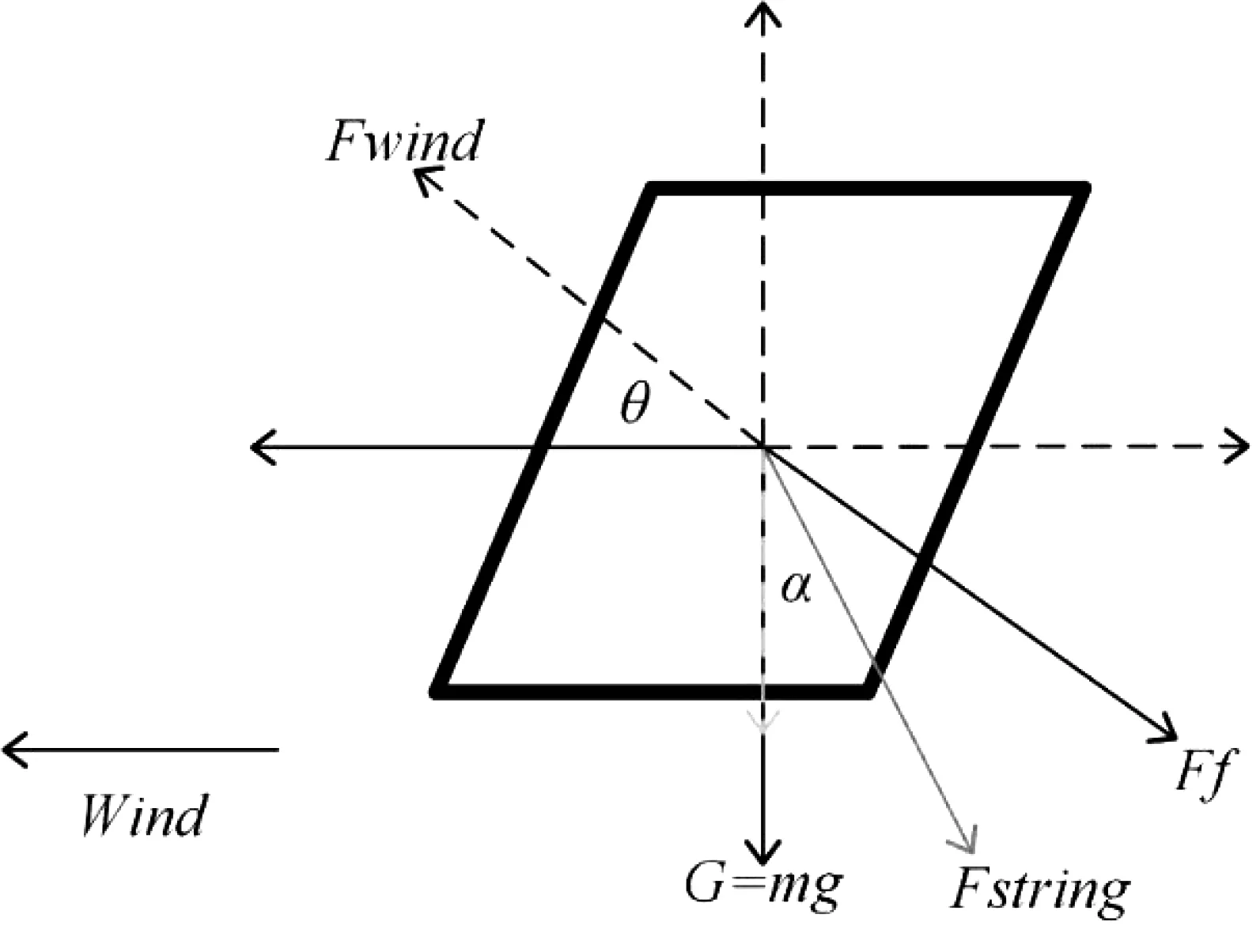
图1 风筝在起飞阶段的动力学受力模型Fig.1 Kinetic force model of a kite in take-off stage

其动力学方程如下：

Fx=Fwindcosθ-Ffcosθ-Fstringcosα

(1)

Fy=Fwindsinθ-Ffsinθ-Fstringsinα-mg

(2)

Ff=k·v2+Fflow≈k·v2

(3)

图1中，Wind代表风向，其对于相对风向成θ，牵引线与风筝质心所在竖直平面的张角为α，Fwind是风力在垂直于风筝平面方向上的分力，Fstring是风筝的牵引线上张力。

其相对于风力方向的反方向，受到空气的黏滞力Fflow与空气阻力k·v2，黏滞力较小，可忽略不计，将阻力视为空气阻力，其是与速度相关的函数。根据伯努利流体力学可推出风力计算公式(在此情形下，为求简洁，根据标准状态情况下的风压计算公式进行计算，且风压的小范围波动相对于风速、重力等较小，对于结果的影响相对也较小)：

(4)

(5)

将(3)、(5)代入(2)中运算取开始放飞状态时有：

(6)

为了使风筝以较大的加速度飞向天空，需要使Fy数值较大。根据式中变量分析，可以通过跑动、借助高速风流等方式获取相对较大的风速v。通过控制引线，使风筝与水平风张角θ=45°。

此过程中，对牵引绳施加的力应适宜，若施力过大，会导致Fy减小或符号变为负值，令起飞失败；若施力过小，在水平方向上：

(7)

使得其横向加速度很大，在横向上的运动位移大于竖直方向上的运动位移，令风筝与水平风张角θ迅速减小，从而(6)式中Fy减小，导致起飞失败。利用“一收一放”，控制合适张角，使得风筝的动力学方程的解在竖直向上的加速度上最优。此外，在初始状态下，可以对风筝施加一个向上的外力，即把风筝“扬”起，突破开始起飞的困难。

风筝起飞时的物理原理和理论最优放飞方式为：在起飞阶段，利用牛顿运动力学将风力、重力和风筝牵引力作正交分解，通过其数学结果来判断风筝的最佳起飞状态。

2 风筝在抬升和高空静止阶段的稳定平衡原理

一般认为，低空风速场不均匀，空气不能看做定常流动的流体。风速的相对大小会给予风筝一个转动力矩(图2)，由力矩的计算公式得到：

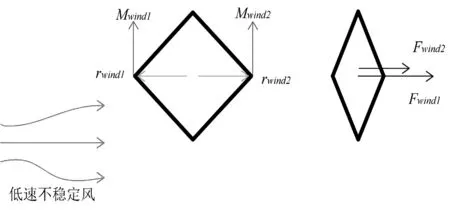
图2 风筝在非定常流动风速场下的受力模型(平旋)Fig.2 Stress model of kite under unsteady wind speed field (flat spin)

Mwind1=rwind1×(Fwind1-Fwind2)

(8)

Mwind2=rwind2×(Fwind2-Fwind1)

(9)

二者是等价的，在此情形下，各自均在数值大小为正时有意义，即在两个相对风力大小不相等的情形下，风筝有旋转的趋势。这里Fwind1、Fwind2是抽象出来的风速场对风筝两翼的作用力，其力矩则是相对质心而言的。

由公式可知，在低空的风速场，风筝除了飞行状态控制外，还需要通过改善自身结构，避免摇摆导致的风筝旋转、飘动和跌落等行为。风筝结构中维持稳定的结构给予质心的力矩称为“稳定力矩”，其一般采用相对对称的结构，从而不改变风筝质心的位置，但是在风筝发生倾斜时，由于配重的二者相对质心的力臂改变，导致力矩改变。以下为简化“配重”型风筝模型及其在侧旋状态下的作用(图3)。

图3 连接配重风筝在姿态改变前后的受力模型(侧旋)Fig.3 Stress model for connecting counterweight kite before and after attitude change(lateral spin)

平旋不会在竖直高度上对风筝姿态造成影响，配重主要是为了避免风筝的侧旋。当风力使风筝侧旋时，风筝的形态如图3(b)所示。此时，两个“配重”对质心的作用效果发生改变，利用力矩公式：

M1=r1×F1

(10)

M2=r2×F2

(11)

(12)

在图中位置，可根据矢量运算法则求得力矩数值大小：

(13)

由于“配重”材料的对称性，其二者受到的重力满足：

(14)

其作用效果表现为使风筝的姿态由侧旋恢复图3(a)的状态。事实上，在偏转后风筝的质心位置有所改变，图中的质心应比图示方向适当右偏，不过稳定力矩的作用效果性质类似。

由(13)可知，F越大，稳定力矩的大小就越大，考虑到风力的大小有限，若“配重”过于沉重，会使风筝起飞困难。

在风筝抬升至高空后，由于细线的作用，(2)中重力有所增加，同时在高空中，风速场减弱，风力大小也减小。在一定的高度上，风筝在以一定的姿态处于较稳定的平衡，即以下方程中满足Fx=Fy=M=0。

Fx=Fwindcosθ-Ffcosθ-Fstringcosα

Fy=Fwindsinθ-Ffsinθ-Fstringsinα-mg

由此可以得到结论，通过“配重”装饰风筝，不仅可以使风筝形态美观，更可以作为稳定力矩的作用者维持风筝在抬升和高空静止阶段的姿态稳定、受力平衡。

3 常见风筝特性的定性分析和生产建议

风筝在较理想的模型基础下有一个拱起的形变效果，以增加稳定性，但由于大多数风筝基本呈轴对称，拱面上风力在x方向的分力抵消，y方向的分力差由人对风筝的拉力平衡，余下垂直于风筝平面的力(z方向)，需要对常见风筝的特性进行定性分析。

风筝主要有两种，即十字风筝和三角风筝。

十字风筝是用横竖两根竹条做骨架，在尾部粘上用蒙面材料做成的长尾条，再将横竹条背面用细线拉紧，使风筝面变成弧形，以增加飞行的稳定性，风筝姿态的稳定主要靠尾带配重，王字风筝的稳定也是类似原理。此类风筝的生产建议是使用轻薄材料减小重量，连接长尾带以增大配重(丝带、燕尾)，采用软质材料利用伯努利原理抬升。

三角风筝飞行状态像伞翼机，主要是靠风筝面向上拱起成弧形达到姿态稳定。该种风筝用宽厚相同的三根竹条做骨架，一根粗细相仿的弹性竹条做撑杆，用尼龙绸做蒙面，弹性竹条可随风力大小改变弯曲程度，进而改变风筝姿态。这种风筝的缺点是风力太大时背面撑杆会弯过头，使迎风面积大幅度减小，升力骤减，风筝会调头向下坠落。此类风筝的生产建议是使用切变模量合适的材料，使其小范围变动内切变模量较小，大范围时切变模量较大，尽量拓宽羽翼，同时考虑质量。

对于串形风筝，平衡配重极其重要，应使用轻软质材料，维持其盘旋飞舞的姿态，一般用颜色较浅的轻杆作配重材料。

图5 利用“配重”稳定的串形风筝(图片来源：网易新闻)Fig.5 String kites stabilized by “counterweights”(source: NetEase News)

图6 非传统放飞式的异形风筝(图片来源：腾讯新闻)Fig.6 Non-traditional flying shaped kite(source: Tencent News)

4 结论

通过建平面模型和动力学稳态分析，从理论上得出了放飞风筝的最佳方式：抛起风筝，给予初始速度和加速度；控制引线“一收一放”，使得风筝线与风筝迎风面处于合适张角；在放飞同时以合适的速度跑动，增加风力的相对大小，借助强风顺势，给予风筝更大的抬升力，使其能够更快到达高空。通过配重力矩分析，得出了风筝在抬升、稳定、生产中的建议：增加配重，使用尾带、拓宽羽翼等方式；使用轻软质材料。存在的不足之处是理论过于趋向于平面化，而未考虑拱形在维持风筝稳态时的重要作用；力矩分析过于定性化，不能很好地应对实际风速场情况。