基于排列熵和CSP融合的脑电信号特征提取

龙佳伟，郑 威，刘 燕，王 玫

(江苏科技大学 电子信息学院，江苏 镇江 212100)

0 引 言

脑-机接口(brain-computer interface，BCI)是一种人脑与外界环境通信的人机交互系统[1]，对于思维正常但神经肌肉系统瘫痪或丧失肢体运动能力患者的康复训练具有重要意义。

研究脑-机接口的关键是脑电信号的特征提取。时频分析法、空域分析法和非线性分析法是脑电特征提取的常用方法。时频分析法主要有小波变换(wavelet transform，WT)、经验模态分解(empirical mode decomposition，EMD)等。空域分析法主要有共空间模式法(common spatial pattern，CSP)、主成分分析(principal component analysis，PCA)等。非线性分析法主要有近似熵(approximate entropy，AE)、样本熵(sample entropy，SE)、排列熵(permutation entropy，PE)、模糊熵(fuzzy entropy，FE)等。其中，共空间模式法能够最大化两类数据之间的方差特征，被广泛应用于运动想象脑电信号的特征提取。Shi Tianwei等人[2]提出了一种新的自适应回归与CSP相结合的特征提取法，该方法能够有效提取脑电信号的特征。Guo Yao等人[3]针对CSP算法的局限性提出了滤波器带分量正则化的公共空间模式方法(filter band component regularized common spatial patterns，FCCSP)，该方法具有显著的优越性，平均分类准确率提高了15.72%。

由于脑电信号具有随机性、非平稳性、非线性等特点，单一的特征无法从多个角度分析脑电信号。近年来，将非线性分析法作用于时频域和空域成为了一种趋势。Syed Salman Ali等人[4]提出了一个基于最大熵的CSP算法，该算法在估计基于样本的协方差矩阵时结合了最大熵原理，分类效果优于传统的CSP算法。Ji Na等人[5]提出了一种基于离散小波变换(discrete wavelet transform，DWT)、经验模态分解和近似熵的脑电特征提取方法，解决了宽频带覆盖问题，使得运动想象脑电信号的分类效果更加显著。Li Yanping等人[6]提出基于局部均值分解(local mean decomposition，LMD)和模糊熵的脑电特征提取方法，结果表明，该方法比经验模态分解法具有更高的分类精度。张学军等人[7]针对模糊熵算法的不足，提出一种基于局部均值分解、模糊熵和共空间模式算法的特征提取方法，有效提高了脑电信号的分类识别率。

以上所提出的算法均是将非线性分析法作用于时频域或者空域，其中模糊熵是在近似熵和样本熵基础上提出的一种非线性分析法，虽然可以表现出某一时间段内左右手运动想象脑电信号间的差异性，但其性能往往受信号长度等多因素的影响[7]。排列熵作为一种非线性分析法，虽然与近似熵、样本熵以及模糊熵一样都是用来表征时间序列的复杂程度，但排列熵获得特征样本集的聚类效果更加明显[8]。2002年，Brandt等人[9]首次提出排列熵(permutation entropy，PE)理论，是一种衡量一维时间序列复杂程度的平均熵参数。张健钊[10]提出了一种基于S变换和排列熵的癫痫脑电信号自动判别方法，该方法在癫痫疾病的诊断方面有较好的应用前景。刘晓凤[11]提出基于多尺度排列熵的面部表情识别方法，该方法能够有效识别与情绪相关的脑电信号。排列熵算法的优势就是用排列的思想来计算重构子序列之间的复杂程度，虽然能够将时间序列的细微变化最大化，但在计算概率分布时，引入该思想会很难察觉内部序列中的异常点。

该文提出了一种基于DWT、并将排列熵算法与共空间模式相融合的特征提取方法(discrete wavelet transform and permutation entropy combined common space pattern，DWT-PECSP)。利用DWT算法分解运动想象脑电信号从而重构出与任务相关的频带，使用排列熵算法提取出判别左右手类别明显的特征向量。针对单一的特征提取方法无法多方面表示脑电信号特征的问题，该文在提取完每段的排列熵特征后，再用CSP提取每段的方差特征，最后将两个特征相融合作为SVM分类器的输入以获得更高的分类精确度。

1 DWT-PECSP算法

1.1 算法流程

整个算法流程见图1。首先对原始信号进行8 Hz～30 Hz的带通滤波处理，接着采用db4小波对EEG信号进行3层小波分解，重构出包含左右手运动想象特性明显的μ和β节律频段，然后分别提取出该频段信号的排列熵和CSP方差作为特征量，并将这两组特征量进行组合。最后，采用支持向量机进行分类识别。

1.2 离散小波变换

小波变换能够有效地分析非平稳信号，通过改变小波窗口的大小来得到信号的时域和频域信息[12]。离散小波变换(DWT)是一种通过对母小波函数进行缩放和移位，将输入信号分解成小波系数集的过程[13]。

设x[n]是离散输出信号，采用Mallat算法对EEG进行小波分解：

(1)

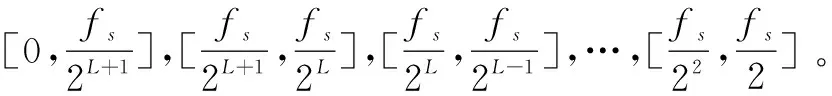
1.3 排列熵

排列熵(permutation entropy，PE)是一种检测信号突变的非线性方法，可以将以前不能定量描述的复杂系统用一种较为简洁的方法描述出来[14]。计算过程简单且具有较高的抗干扰能力和较好的鲁棒性。

假设{xi,i=1,2,…,N}是个一维的时间序列，嵌入维数为m(m>1),时间延迟为τ(τ>0)，组成一个能够使当前序列依次通过的窗口(m,τ)，对该一维时间序列进行像空间重构：

(2)

矩阵的每一行作为一个重构分量：

Yj=[xj,xj+τ,…,xj+(m-1)τ],j=1,2,…,k

(3)

按照数值大小的升序方式对重构分量进行排列，排列方式总共有m！种。将P1,P2,…,Pk表示每一种排列情况出现次数的概率，排列熵是由 Shannon 的方式来定义的：

(4)

排列熵值Hp(m)的大小可以表示一种时间序列的复杂程度。越有序的时间序列所对应的排列熵的值越小，越复杂的时间序列所对应的排列熵的值越大。

1.4 共空间模式法

CSP是一种空域分析法，算法的原理是利用矩阵对角化找到一组最大化两种类型任务方差的最优空间滤波器，从而得到具有最大分辨能力的特征向量[15]。该算法主要处理的是两类问题，是主成分分析法的延伸[2]。

算法具体步骤为：

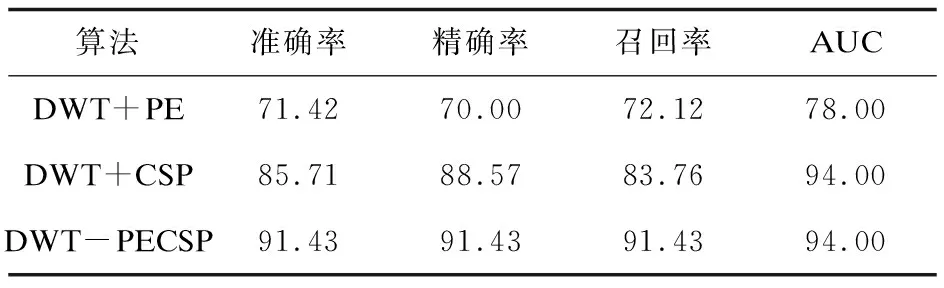
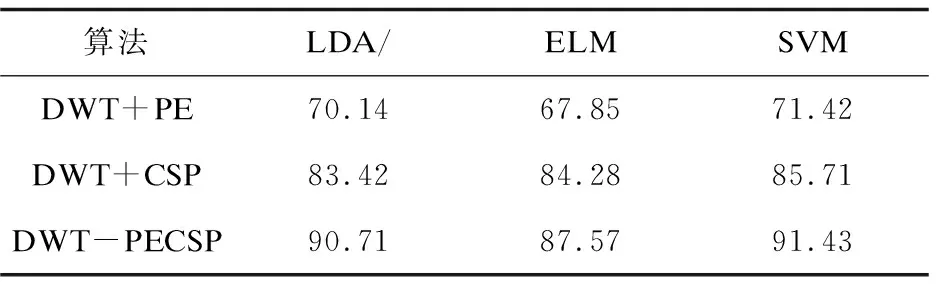
步骤1：将离散小波变换重构得到的μ节律和β节律频段信号作为CSP算法的输入向量，记作X1∈RN×T和X2∈RN×T，其中N为通道数，T为采样点数。当N

(5)

(6)

(7)

步骤3：对特征值进行降序排列得到白化矩阵P，并对R1和R2进行变换和主分量分解。

(8)

(9)

λ1+λ2=I

(10)

其中，I为单位矩阵。

步骤4：计算投影矩阵W。

W=BTP

(11)

步骤5：将原信号X1和X2经投影矩阵W滤波得到矩阵Z1和Z2:

Z1=W*X1

(12)

Z2=W*X2

(13)

2 实验分析

2.1 实验数据

实验采用2003年BCI竞赛的Graz数据集(data set III) 。实验受试者为一名25岁的健康女性。实验范式是受试者以放松的状态坐在椅子上，根据屏幕的随机提示，通过想象左手或右手的动作来控制目标移动。如图2(a)所示，实验的总时长是9 s。t=0 s-2 s受试者处于放松状态，t=2 s时，屏幕上显示时长为1 s的“+”提示符表明实验开始。t=3 s时，会出现一个向左或向右的箭头，受试者按照箭头的方向进行对应的运动想象，t=9 s实验结束。如图2(b)所示，实验采集了C3、Cz和C4通道的脑电信号，信号的采样频率为128 Hz，并进行了0.5 Hz～30 Hz的带通滤波。其中，该文只选取了包含左右手运动想象信息最丰富的C3和C4通道，Cz作为参考电极。整个实验共进行280次，分7组运行，每组40次。实验数据包括训练样本和测试样本各140次。其中，分别想象左右手运动任务各70次。

2.2 数据预处理

大脑在做运动想象任务时，大脑同侧运动感知区μ节律和β节律能量或幅度会升高，这就是事件相关同步(event related synchronization，ERS)现象，而对侧μ节律和β节律能量或幅度会降低，这就是事件相关去同步(event related synchronization，ERD)现象[16]。因此，ERD/ERS现象可以对运动想象信号进行有效的识别[17]。该文首先对原始信号进行8 Hz～30 Hz的带通滤波处理，然后对C3和C4通道上的EEG信号进行傅里叶变换得到C3和C4通道想象左右手运动的脑电信号频谱图，如图3所示。通过频谱分析，选取ERD/ERS最为明显的频段信号进行接下来的特征提取和分类。

由图3可得，受试者在8 Hz～30 Hz频段范围的运动想象实验中，其出现ERD/ERS现象最明显的是μ节律(8 Hz～12 Hz)和β节律(18 Hz～26 Hz)这两个频率段。因此，接下来该文将通过离散小波变换分解重构出μ和β节律的频段信号进行后续的特征提取和分类。

表1 小波分解后各层频带范围

由于本实验采集信号的频率为128 Hz，因此该文使用db4小波对预处理后的运动想象脑电信号进行3层小波分解与重构。由表1可以看出，μ/β节律主要包含于小波分解的细节信号D2和D3中。故该文对第2层、第3层细节信号进行重构。重构后的C3和C4通道的脑电信号如图4所示。

2.3 特征提取

2.3.1 排列熵特征提取

使用排列熵算法对重构后C3和C4通道上包含μ/β节律的频段信号进行特征提取。该文在提取排列熵特征时，选取的参数m取值为4，τ取值为1，采用窗口长度为1 s，采样点数为128，窗移为1个采样点来计算各个时间窗的熵值，从而获得运动想象脑电信号C3和C4通道排列熵的时间序列。由图5(a)可以看出，在4.5 s～7.5 s期间，发生ERD/ERS现象。当大脑想象左手运动时，C3通道能量增加，排列熵值变小，产生ERS现象；当大脑想象右手运动时，C3通道能量减少，排列熵值变大，产生ERD现象。由图5(b)也可以很明显地看出，在4.5 s～7 s期间，发生ERD/ERS现象。在想象右手运动时，C4通道能量增加，排列熵值变小，产生ERS现象；在想象左手运动时，C4通道能量减少，排列熵值变大，产生ERD现象。由此可见，提取脑电信号的排列熵作为特征也可以表现出ERD/ERS现象。

2.3.2 CSP特征提取

为了使两类向量之间的差异度更大，该文也采用共空间模式算法对重构后C3和C4通道上包含μ/β节律的频段信号进行共射投影。提取CSP特征时，选取的参数m取值为1，得到的特征数目为2，如图6所示。从图6中可以很直观地看出左右手的区分效果。由此可见，对于两类的左右手运动想象信号，经过CSP处理，左右手任务的区分效果更加明显。

2.4 脑电信号分类

2.4.1 支持向量机

支持向量机(support vector machine, SVM)是一种针对二分类问题的机器学习方法。其目的是在结构风险最小化的基础上保证学习算法具有良好的泛化能力。SVM具有适应性强、分类能力好以及计算效率高的特点[18]。

SVM分类的基本思想是通过一个合适的非线性变换将输入空间映射到一个高维空间，然后在这个新空间中寻求广义最优分类面，使它能够将两类样本无错误地分开，同时使分开的两类样本的分类间隔最大。对于非线性映射，核函数的选择尤为重要，不同的核函数取得的分类效果是不同的。本研究选用的核函数为径向基核函数Rbf，误差因子C取0.8，实验总次数为280，使用前140次作为训练集输入SVM进行训练，然后用后140次作为测试集来测试训练的效果。

2.4.2 分类结果分析

该文利用四个指标对左右手运动想象信号的分类结果进行评估，分别是准确率、精确率、召回率和AUC(area under curve)。准确率表示预测受试者进行左右想象的正确率，精确率表示衡量模型对某一类预测的准确度，召回率表示预测出的受试者进行左右想象的组数占实际进行左右手组数的比例，AUC为ROC曲线和坐标轴所围面积的大小。AUC值的大小可以作为分类器分类效果优劣的指标。AUC值越大，表明分类器的分类效果越好[19]。

利用提出的基于排列熵与CSP融合的算法对脑电数据进行分类。为了验证该算法能够有效分类脑电信号，采用基于DWT的排列熵、基于DWT的CSP以及两者相融合的算法进行特征提取，并使用SVM进行分类。

三种不同特征提取算法的分类准确率、精确率、召回率和AUC指标见表2。

表2 实验结果 %

由表2的实验结果可知，提出的特征提取算法的分类准确率达到91.43%，相比于单一使用排列熵算法的分类准确率71.42%和CSP特征提取算法的分类准确率85.71%有了明显的提高。说明该算法能够提高运动想象脑电信号的分类准确率，更加验证了算法的有效性。

将近几年其他文献中提取运动想象脑电特征的分类算法与文中实验结果相对比，如表3所示。从表3可以看出，与文献[6]中基于LMD和模糊熵的多特征融合提取算法相比，准确率高6.07%，这是因为文中算法还结合了CSP算法，使得两类向量之间的差异度增大，提高了分类准确率。总体来看，文中算法的准确率明显高于其余四组的分类准确率。

表3 与其他文献的分类准确率比较

2.4.3 不同分类算法的分析比较

为了能够更好地验证分类算法的有效性，将单一特征的特征向量和融合后的特征向量用线性判别法(LDA)和极限学习机(ELM)两种分类方法进行分类，并将其结果与SVM的分类结果相比较，结果如表4所示。

表4 不同分类算法的准确率比较 %

由表4可知，对于排列熵特征，线性判别法和ELM的分类准确率分别为70.14%和67.85%，而SVM的分类准确率达到了71.42%；对于CSP特征，线性判别法和ELM的分类准确率分别为83.42%和 84.28%，而SVM的分类准确率达到了85.71%。对于融合后的特征，线性判别法和ELM的分类准确率分别为90.71%和87.57%，而SVM的分类准确率达到了91.43%。可见对单一特征和融合后的特征向量，SVM的分类性能都比其他两种分类算法要好。线性判别法是一种常用的线性统计学分析法，操作简单，而且不需要繁复的计算。但由于EEG的非线性，往往导致识别率不高。ELM是一种极限学习机，是用来求解单隐层神经网络的算法。在保证学习精度的前提下比传统的学习算法速度更快。但ELM参数的不确定会导致整体分类精度下降。

分类结果表明，SVM相较于其他两种分类算法可有效地对运动想象EEG进行分类。体现出SVM结构风险最小化和分类间隔最大化的特点，对于解决小样本、非线性、高维度和局部极小点的问题时效果显著。

3 结束语

该文提出一种将非线性域作用于时频域和空域的特征提取法。在使用小波变换重构出特定频段的基础之上，利用排列熵算法衡量运动想象脑电信号复杂度特性以及共空间模式加大左右手特征向量差异度，从而提取出易于区分的特征向量。实验采用的数据集是BCI2003中的Data set III，实验结果表明，该算法的最高分类准确率高达91.43%，优于单一使用排列熵和CSP的特征提取算法。