形变预测中两种模型的对比研究

刘世城 唐斌 金春阳

（1、成都理工大学地球科学学院，四川 成都 610059 2、桂林理工大学测绘地理信息学院，广西 桂林 541006）

形变是指如今的钢筋混凝土房子会随着时间的推移而产生一些形变，例如下沉、平移以及扭转等现象。而形变监测的目的，就是要得到目标在时间和空间上的关系，最后做出几何分析与报告。其意义在于，获取了目标的形变数据，然后及时分析，当即做出相关有效的控制，避免其出现问题后对周边环境造成不可挽回的局面。

如今，国内已有很多学者对形变问题进行了大量的研究。例如，以高层建筑静态形变监测为研究对象，分析了高层建筑形变监测的范畴，探讨了形变监测方案的设计思路和观测周期的确定方法，在此基础上，探讨了建筑形变监测的具体方法[1]；以高层建筑为形变监测对象，进而探讨了形变监测方案的设计思路和观测周期的确定方法，在此基础上，探讨了建筑形变监测的具体方法[2]；以高层建筑形变为研究对象，分析了高层建筑形变的一些主要原因以及形变监测在高层建筑中的重要性。从而提出高层建筑形变监测方案的设计思路及有效控制措施，为提高高层建筑的质量和保障人们生命安全提供了理论研究[3]，还有从高层建筑形变监测概述入手，探讨了高层建筑形变监测方案设计及监测措施[4]。

本文是以广西某小区的形变监测数据为基础，以数理统计与拟合预测为数据处理的方式，运用图表对比的方式，绘制出累计沉降量与观测时间的关系图和本次沉降速率与观测时间的关系图。文中还阐述了数据处理中常用的回归分析法，然后运用Matlab 进行数据分析，确定出监测点的线性函数模型与非线性函数模型，用回归模型与灰色系统模型进行拟合预测，将拟合预测结果进行对比，进而得出形变预测中两种模型的精度对比。

1 研究区概况与数据来源

1.1 研究区概况

研究区位于广西某地，其东面与北面依靠着阳江路和桃花江，交通顺畅便利，南面与徐家村相邻，西面相邻的是农田。

1.2 数据来源

文章所用的数据均是对研究区小区进行的二等水准测量所获取得的形变监测实测数据，数据来源可靠。沉降监测数据工作从2017 年10 月27 日开始，到2017 年12 月19日。

2 数据分析与预测

2.1 图表法分析数据

图表法主要是对监测数据进行基本处理之后，所绘制形成的图表来表示各阶段的监测结果。通过图表法可以很直观、形象地反映出每一个测点的变化以及变化趋势。

根据沉降监测的观测结果，将全部数据分为局部和整体进行图表法分析。将2017 年10 月27 日到2017 年12 月5日划分为沉降观测的局部阶段，然后2017 年10 月27 日到2017 年12 月19 为沉降观测的整体阶段。

局部阶段沉降变形监测点的沉降量与时间关系曲线图如图1 所示。

图1 测点累计沉降与观测时间关系图

整体阶段沉降变形监测点的沉降量与时间关系曲线图如图2 所示。

图2 测点累计沉降与观测时间关系图

2.2 回归分析法预测数据

根据回归分析，对各阶段的沉降监测数据进行计算并拟合出线性函数模型，求出自变量与因变量量之间的关系，最终推算出测点沉降的变化位移量。该方法主要用于分析和预测各阶段的监测数据。

面对建筑物坍塌等灾害事故，人们认识到变形监测只是手段，而科学预报才是目的。文章利用研究区的沉降实测数据，通过线性分析与非线性分析进行对比，得出不同的预测结果，进而比较得出线性分析与非线性分析的预测精度对比结果。

2.2.1 一元线性回归分析

此法分析是将自变量与因变量联系起来的。对于本次的沉降变形监测，自变量为观测时间，因变量为观测点的沉降数据。

根据观测点的观测值，用一元线性方程去拟合，然后运用Matlab 进行预测，最后用得出的线性方程去预测未来的观测时间所对应的观测值大小。

一元线性回归方程的数学模型为：

其中，f(x)是预测对象，称为因变量；x 是影响因素，称为自变量；a、b 均为待定的回归系数；ε 是随机误差[5-7]。

2.2.2 一元高阶非线性回归分析

一元高阶非线性回归分析亦是将自变量与因变量联系起来。自变量为观测时间，因变量是观测点的沉降数据。

根据观测点的观测值，用一元高阶方程去拟合，然后运用Matlab 进行预测，最后用得出的非线性方程去预测未来的观测时间所对应的观测值大小。

一元高阶非线性回归方程的数学模型为：

由于观测点比较多，所以选择比较有代表性的点来分析。从图2 中可以看出，测点1 呈上升的趋势，而测点4 呈下沉的趋势，并且是累计沉降量下沉最大的几个观测点。

根据上述方法分析代表性上升的观测点，得出由测点1的前23 组数据拟合与预测得到如图3、图4 不同的线性与非线性拟合图。在下图中，虚线表示测点实际累计沉降量的走势，实线表示由Matlab 根据实际数据计算出测点的线性函数或非线性函数与其预测值，其中横坐标“24-30”数值表示在观测频率一样下，未来的观测时间，其相对应的纵轴值为累计沉降量的预测值。

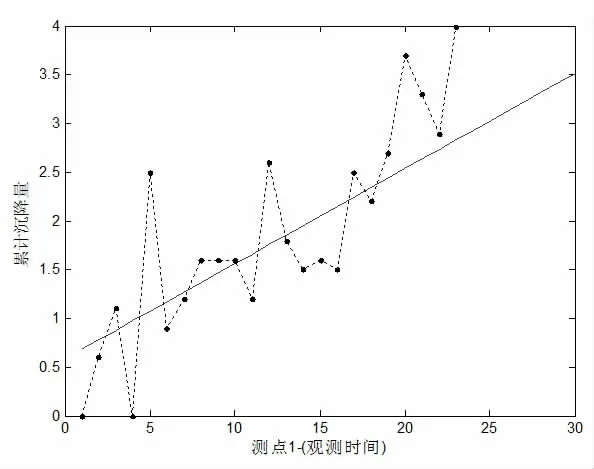
图3 测点1 线性拟合图

测点1 的拟合方程分别如下：

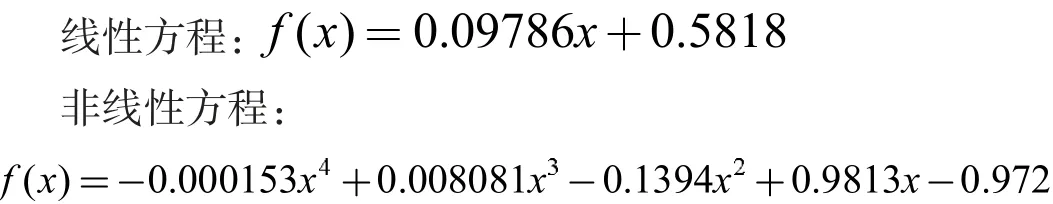
由图4 来看，预测短时间内的数据比较相近，但是之后其急剧下降，所以非线性回归分析预测在长时间来说，会出现误差比较大的可能性。

图4 测点1 非线性拟合图

根据上述方法分析代表性下沉的观测点，得出由测点4的前23 组数据拟合与预测得到如图5、图6 不同的拟合图。

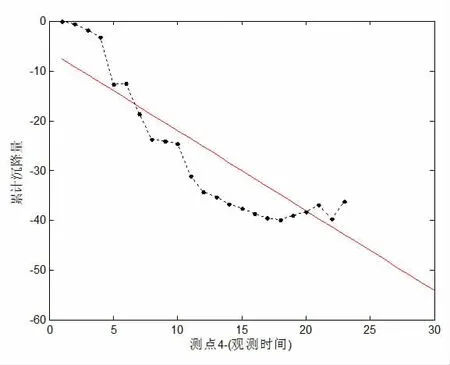
图5 测点4 线性拟合图

图6 测点4 非线性拟合图

拟合方程分别如下：

非线性方程：

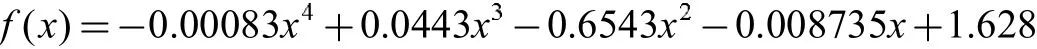
2.3 灰色系统模型预测

灰色系统理论与方法的核心是灰色动态模型，其特点是生成函数和灰色微分方程。灰色动态模型是以灰色生成函数概念为基础，以微分拟合为核心的建模方法，灰色系统理论认为：一切随机量都是在一定范围内、一定时段上变化的灰色量和灰过程，对于灰色量的处理不是寻求它的统计规律和概率分布，而是将杂乱无章的原始数据列，通过一定的方法处理，变成比较有规律的时间序列数据，即以数找数的规律，再建立动态模型[8]。对于原始数据以一定方法进行处理，其目的是为建立模型提供中间信息和将原始数据的波动性弱化[8]。

GM(1,1)建模思想是直接将时间序列转化为微分方程，从而建立抽象系统的发展变化动态模型[9]。

根据灰色模型GM(1,1)的基本步骤[9]，结合研究区实测的沉降数据，通过Matlab 进行分析预测，最后得出几个代表性观测点的预测值、关系图和对应的灰色预测模型。其上升测点1、测点11 和测点12，下沉测点4、测点5 和测点16 的预测图如图7 所示。

图7 各测点灰色模型预测图其中各测点的灰色预测模型中a、b 的值计算结果如表1所示。

表1 灰色预测模型中a、b 的值

3 精度对比

文章利用回归分析模型和灰色系统模型预测了较有代表性的沉降观测点，将两种模型的预测值与实际观测值相减得出观测点的残差，此残差大小即表示为各个模型的精度大小。

其中，测点1 和测点4 作为代表性观测点的预测值及其残差的计算结果如表2 所示：（表中残差1 表示线性模型预测累计沉降量与实测累计沉降量之差；残差2 表示非线性模型预测累计沉降量与实测累计沉降量之差；残差3 表示灰色模型预测累计沉降量与实测累计沉降量之差）。

表2 测点1 和测点4 的各模型预测累计沉降量及其对应残差值

4 结论

综上所述，运用回归模型和灰色系统模型进行样本预测，所得出的预测数据和计算出的残差数据结果，得出精度较高的模型为高阶非线性回归分析模型。

当用图表法分析数据时，由于观测数据比较少，所以用Matlab 对沉降观测数据进行拟合以及进行一元线性回归分析和GM(1,1)模型预测时，所预测的数据与实际上的有一些差别，并且形成的线型和实际上的线型不能完全地重合，在后续的研究中，可以增加数据量和运用其它模型来分析预测变形结果，为监测工作提供更有利的数据支撑。