铜绿山矿上向分层充填法数值模拟及充填体强度优化

马生徽，刘俊，赵朋飞

(1.三林万业（上海）企业集团有限公司，上海 200000； 2.武汉华咨同惠科技有限公司，湖北 武汉 430070)

0 引言

随着充填采矿技术的不断进步及矿山安全环保与尾砂综合利用的需要，充填采矿法的应用越来越广泛。充填采矿法的安全性与经济效益主要取决于胶结充填体强度，充填体强度过高会造成生产成本的增加，过低会造成矿山开采安全问题。因此充填体强度设计既需要考虑保障开采安全，也需要考虑降低成本。

国内外学者对充填体强度设计提出了很多理论与方法，包括经验公式法、数学力学模型法和数值模拟分析法。经验公式法如蔡嗣经教授利用7个国家的13个矿山实际采用的充填体强度数据，得出胶结充填体的强度和高度是一种曲线关系[1]。李爱兵教授等综合有限元分析与监测结果，采用半经验公式计算安庆铜矿120 m高充填体自立高度所需的实际强度[2]。而数学力学模型法是在岩体充填体力学特征研究的基础上，简化抽象出可以表征胶结充填体基本力学特征的分析模型，借助于数学力学方法获得胶结充填体应力分布特征，包括太沙基强度计算法[3]，Mitchell强度模型法[4]，卢平强度公式[5]，高水模型[6]等。数值模拟分析法是利用计算机软件，模拟矿山开采充填，对充填体-岩体系统进行应力分析的方法，具有建模方便、计算快速、适应性强的优点，在充填体强度设计中的应用越来越多[7-10]。

1 工程概况

目前铜绿山矿普遍使用上向分层充填法。矿山中段高度为60 m，采场一般垂直走向布置。每个采场宽8～10 m，长为矿体厚度，划分矿房矿柱回采，底柱高8 m。中段划分为4个分段，每个分段3～4个分层，每分层回采高度一般为3 m，自一分段向四分段由下而上逐步回采。分层矿石出完后，立即对空区进行充填，充填高度一般为3 m，一步骤矿房、拉底层及铺面采用胶结充填，二步骤矿柱采用全尾砂非胶结充填。胶结充填料水泥、尾砂的配比为1∶5～l∶10；尾砂和胶凝材料的质量浓度≥65%；充填体强度≥2 MPa。设计充填强度根据工程类别确定，存在胶结充填体强度较高造成充填成本高的问题。本文通过FLCA3D软件模拟开采充填过程，从充填体受力特征出发，优化充填体强度，实现降低充填成本与保证安全开采的目的。

2 数值模型及计算方案

2.1 计算模型的建立

利用FLCA3D自带建模命令建立采场结构参数数值计算模型，如图1所示。整个模型宽200 m，高300 m，厚10 m。共6300个单元与13 222个节点，中段高度为60 m，采场宽度为10 m。围岩范围是开挖区的3倍尺寸。为了建模与赋值方便，将模型划分为8个部分，中间7个单元体为采场，包括矿房与矿柱，四周为围岩。

图1 采场结构参数数值计算模型

2.2 初始条件和计算参数的选取

初始应力采用应力边界法在模型边界施加应力约束，先计算原岩应力场平衡，得到采场开挖前的最初应力状态。在充填采矿过程中添加位移边界 条件，然后模拟开挖充填，得到采矿过程前后的矿岩应力状态。矿岩力学参数通过矿山已有资料，矿岩采用摩尔-库伦准则，采空区采用空模型，变形设置为大变形。计算参数见表1。

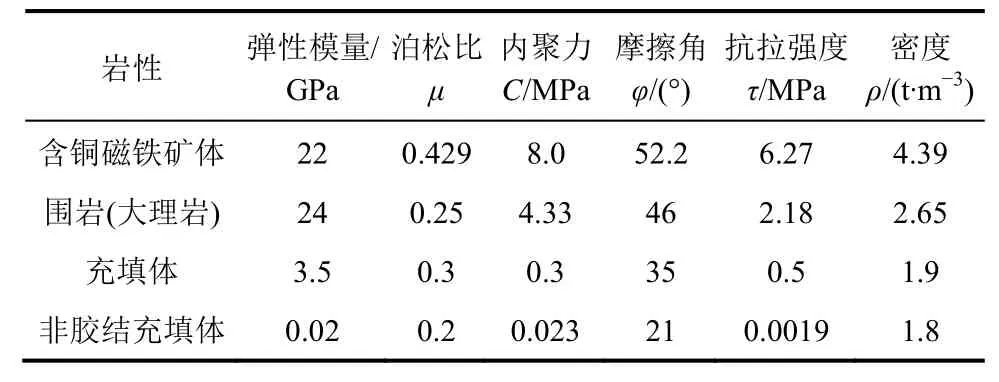
表1 矿岩物理力学参数

2.3 计算方案的确定

根据矿房矿柱的回采充填顺序，将数值模拟划分为4步骤进行，一步骤回采2，4，6号矿房，二步骤胶结充填2，4，6号矿房；三步骤回采1，3，5，7矿柱；四步骤全尾砂非胶结充填1，3，5，7矿柱。上述计算过程可以模拟出整个中段开采过程，每个阶段的计算均按顺序在前一阶段计算的基础上连续进行，从而客观地反映了开采过程中矿岩应力状态的发展过程，以便分析充填采矿过程中矿岩与胶结充填体应力变化与分布特征，为充填体强度优化提供依据。由于实际生产充填体固化脱水收缩，采空区接顶难度大，数值模拟以充填体未接顶进行计算。

3 计算结果及分析

3.1 矿岩应力分析

图2为一步骤至四步骤的最大主应力分布图，从图2可以看出，一步骤矿房开挖过程中，应力向采空区两侧转移，采空区两侧形成应力集中区，矿房顶底板形成应力下降区。应力集中区出现在采空区四周拐角处。二步骤充填矿房后，整体应力分布特征基本和一步骤保持一致，但应力最大值有所下降，说明充填可以缓解应力集中现象。三步骤矿柱在开挖后应力进一步向围岩转移，整体应力分布状态发生改变，采区顶底板的卸压区范围变大，两侧的应力集中区域也变大。四步骤矿柱采空区充填后，最大主应力分布状态和三步骤也基本保持一致，说明开挖对应力分布状态起决定作用，充填对整体影响不大。另外充填体的整体应力值较小，应力集中主要分布在围岩区域，说明地压主要由围岩承担，充填体只起到应力转移作用。

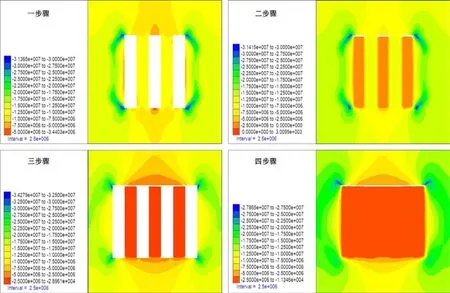
图2 最大主应力分布

3.2 塑性区分析

图3为一步骤至四步骤的塑性区变化情况。一步骤矿房开挖后，矿房两侧的矿柱区域出现剪切塑性区，3号、5号矿柱的剪切塑性区集中在中部，与其单向受力状态有关。1号、7号矿柱的剪切塑性区出现上下区域，与其应力集中有关。二步骤矿房胶结充填后，对塑性区分布影响不大，保持与一步骤相同的塑性区分布。三步骤矿柱开挖后，两侧围岩出现剪切塑性状态。四步骤矿柱采用非胶结充填完毕后，围岩塑性变化不大，矿柱周边区域出现剪切与拉伸塑性状态。采用胶结充填体的矿房在第三步骤中出现塑性状态，矿柱充填后塑性区消失，最终充填体保持稳定。

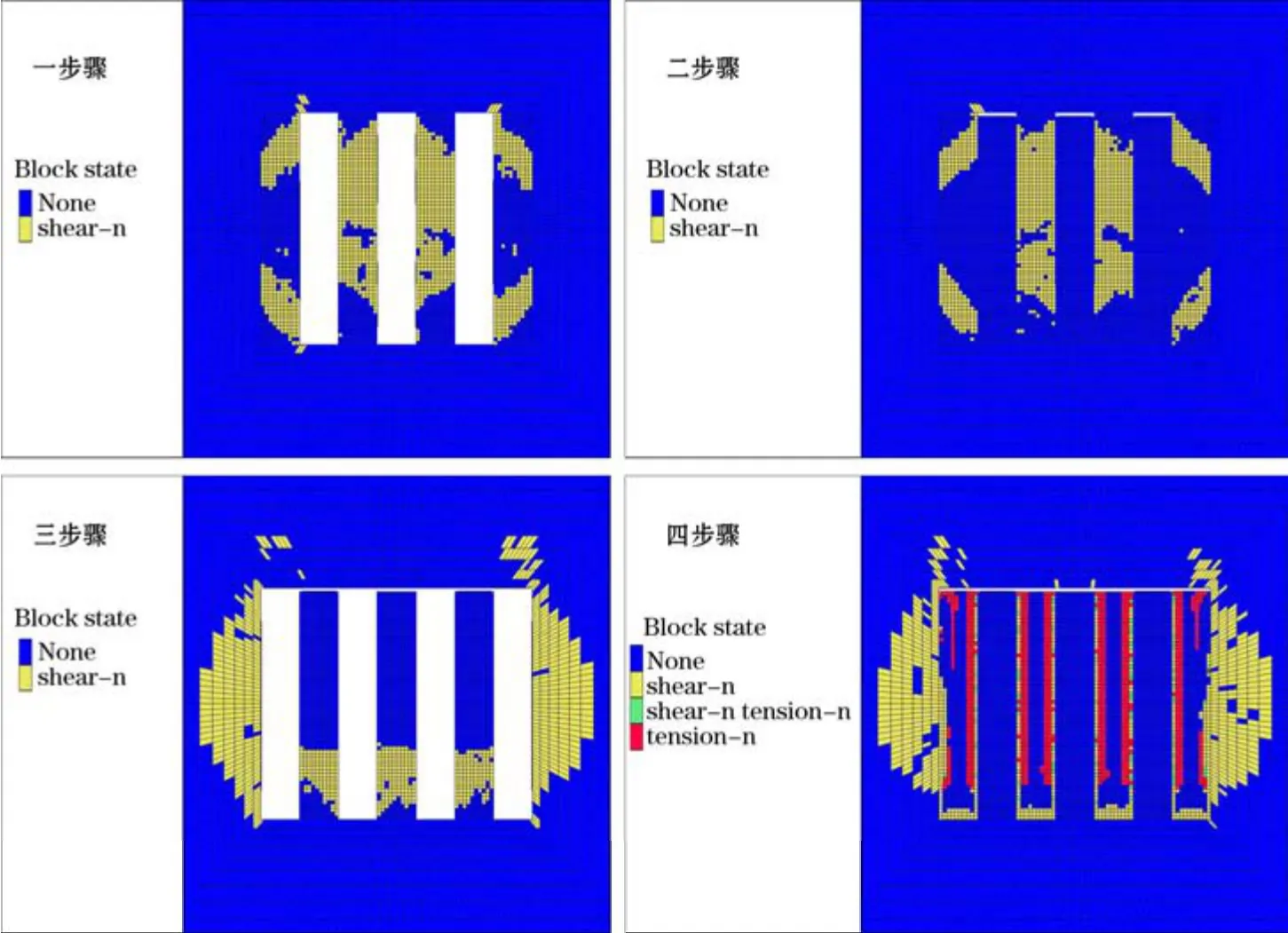
图3 塑性区分布

3.3 胶结充填体受力分析

图4为矿房胶结充填体的最大主应力分布图， 二步骤后胶结充填体主体区域的应力值为1 MPa左右。整体应力分布集中在充填体顶底角及周边。充填体四周应力值大，但其面积较小，充填体内部应力值较大，分布范围较大。三步骤后胶结充填体的应力分布转化为分层分布，应力值主要集中在0.5～2 MPa之间，底部有小部分应力值达到4.05 MPa。四步骤后胶结充填体的最大主应力分布规律仍然是分层分布，但出现一定的拱形状态。总体而言，胶结充填体的受力状态并非均匀，在垂直方向上，下部的应力值较大，上部的应力值较小。在水平方向上中间应力值比两侧应力值大。因此采用统一强度充填采空区未考虑充填体实际受力特征，设计的充填体强度偏大，造成充填成本高。

图4 胶结充填体最大主应力分布

4 胶结充填强度优化

通过数值模拟可知，开采充填过程中产生的应力集中主要由围岩承担，充填体主要起到应力转移作用，充填体在采空区中以自立为主，最终充填体受力状态呈现非均衡的层状拱形分布。矿山充填强度设计偏于保守，未充分考虑充填体力学状态与作用，造成水泥使用量和充填成本的增加。根据垂直方向上充填体受力特征，设计与之强度匹配的胶结充填体，能在保证安全与经济的前提下实现强度优化设计。因此，对数值模拟中胶结充填体的最大主应力进行定量分析，充填体垂直方向的最大主应力值见表2。

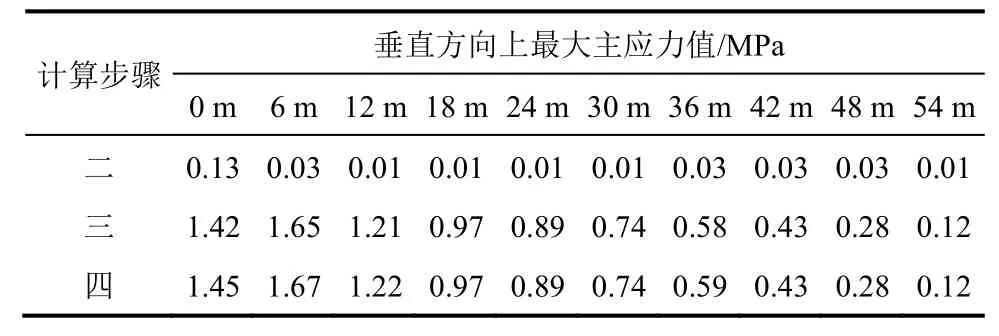
表2 垂直方向上充填体最大主应力值

由于充填体主要为受压破坏，当充填体两侧回采揭露形成空场时，充填体处于单向受力状态，根据摩尔-库伦准则，当单轴压缩破坏时，σ2=0，σ1=σc，因此充填体所需抗压强度应大于最大主应力σ1。根据表2充填体应力分布特性，在采场垂直方向上划分为若干个单元进行充填，设计充填体强度如下：回采高度为0～12 m时，设计充填强度为1.6 MPa；回采高度为12～24 m时，设计充填体强度为1 MPa；回采高度为24～36 m时，设计充填体强度为0.8 MPa；回采高度为36～60 m时，设计充填体强度为0.5 MPa。胶结充填体优化后平均强度为0.9 MPa，而矿山实际充填体强度不小于2 MPa。设计充填体强度的降低意味着水泥的使用量减少，可直接降低充填成本。

5 可靠性验证

利用数学力学模型法计算充填体强度来验证数值模拟优化结果的可靠性，本文选取了表3中的3种公式[4-6]。充填体强度参数如下：内聚力C=0.3 MPa，内摩擦力φ=35°，充填体密度ρ=1.9 t/m3，胶结充填体宽度与长度即矿房宽度B=10 m，长度L=20 m，充填高度H=60 m，代入公式计算的充填体强度分别为0.26 MPa，0.204 MPa，0.36 MPa。3种方法计算的数值比较接近，且均小于通过数值模拟设计的充填体强度值，说明通过数值模拟设计的强度值有一定的合理性。

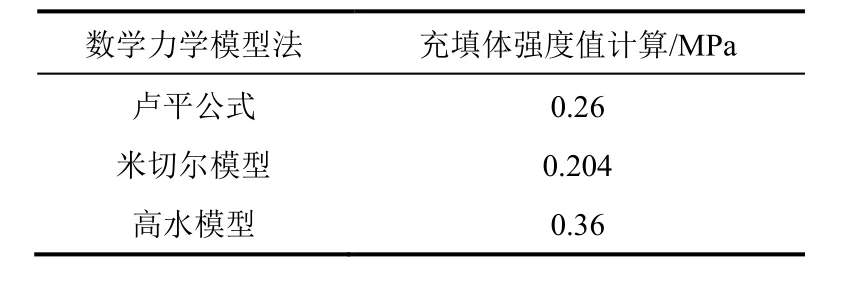
表3 数学力学模型法计算充填体强度

6 结论

从数值模拟的结果来看，采用单一的胶结充填体强度对采空区充填与充填体实际受力状态不匹配。因此，应根据胶结充填体的受力状态设计与其应力状态匹配的强度，避免充填体强度设计过大的问题，有利于节约胶结材料使用量，降低充填成本，并通过典型的数学力学模型验证了基于数值模拟充填体强度设计的合理性。