矩形巷道锚杆中性点位置特征研究*

任何，宋义敏，张军徽

(北方工业大学 土木工程学院，北京 100144)

0 前言

随着矿山开采向深部发展，地应力呈非线性增加。开采时软弱煤层在高地应力作用下容易发生失稳破坏，对采矿工程造成极大的危害[1-3]。因此，开展巷道支护研究具有十分重要的意义。

近年来，巷道支护已经成为煤矿开采领域的热点[4-10]。其中，锚杆及锚索等支护结构广泛应用于各种岩土工程中[11-14]，国内外学者们为此开展了大量的研究工作。程良奎等[13]根据模型试验和现场试验,对摩擦式锚杆的作用原理进行了探讨，揭示了摩擦式锚杆的支护效果和先柔后刚的特点；杨庆等[14]等根据局部变形理论，推导出全长注浆岩石锚杆的界面剪应力和轴向载荷的分布函数；李桂臣等[15]采用弹塑性力学理论，推导出注浆前后锚固剂与孔壁之间剪应力分布的理论解析式；王正义等[16]将冲击应力波进行合理简化，建立了平面P波与圆形锚固巷道相互作用简化模型；宋洋等[17]在局部变形理论基础上，对全长黏结型锚杆锚浆界面破坏类型的锚固机理进行了分析研究；LI等[18]建立了三种锚杆的分析模型，指出现场锚杆具有拾取长度、锚固长度和中性点；姚显春等[19]以中性点的轴力为集中力，由半无限体受集中力作用的Mindlin解导出中性点以内锚杆界面剪应力的分布规律；朱训国等[20]结合中性点理论，对影响中性点位置的因素进行了分析，得出了影响锚杆中性点位置的相关因素。虽然学者们在锚杆及锚索等支护结构的研究方面取得了很多有意义的成果，但大多数研究都是针对同性岩体、圆形洞室，没有考虑层状结构的影响，因此，本文以全摩擦锚杆为例，通过理论分析对矩形巷道层状围岩中的锚杆应力分布特征进行探究。

本文通过将煤层顶板简化为只发生剪切变形的剪切梁模型，对开挖后煤层的横向变形进行分析；进而以煤层的横向变形为参量，结合锚杆已有的本构解析解，建立矩形巷道锚杆应力计算模型，对其中性点位置特征进行分析。

1 锚杆应力计算模型

图1为嵌入煤层的锚杆，锚杆承受的剪应力应该分为两部分。首先，巷道开挖后，煤层岩体向采空区发生变形，锚杆对岩体变形产生约束作用。即煤层岩体横向变形对锚杆产生了剪应力τ1。而随着煤层变形向深部递减，作用在锚杆上的剪应力τ1逐渐减小，即锚杆巷道端的部分对深部的部分产生拉拔作用，引发了煤层岩体施加给锚杆的另一个剪应力τ2来抑制这种拉拔趋势。

图1 煤层中的锚杆

在嵌入锚杆的煤层取单元体b如图2所示，假设原始应力条件下煤层岩体横向变形为du，而设置 锚杆后，围岩的应力分布重新调整，煤层岩体的实际变形变为dub；变形的减小量dur则是由锚杆与煤层岩体间相互作用，使得煤层岩体中应力增加了Δσr的结果。

图2 煤体单元

dx左端界面平衡方程为：

式中，S为锚杆影响范围，A为锚杆截面面积。

将式（2）代入式（1），得到锚杆轴应力与煤层岩体变形关系式：

锚杆单元平衡方程为：

即：

式中，db为锚杆截面直径。

则原始应力条件下的煤层岩体变形引发的剪应力τ1为：

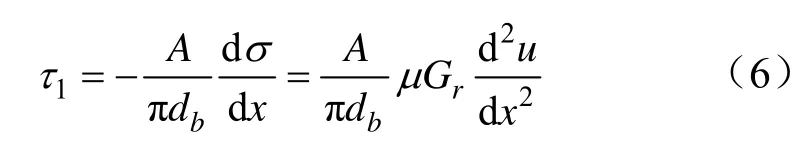
根据I W FARMER拉拔作用下锚杆剪应力衰减公式，将其应用于锚杆可得到：

煤层岩体变形引发的剪应力τ1导致了锚杆内部dt处轴应力的差值dσ，dσ在x处引发了接触面施加给煤层岩体的剪应力τ2。则dt处轴应力在x处引发的剪应力为：

则x处的τ2为：

所以，煤层岩体中锚杆剪应力计算公式为：

2 剪切梁模型

将煤层上顶板简化为只考虑剪切变形的剪切梁，假设煤层岩体为均匀、各向同性，底板为刚性，忽略其变形，进而建立剪切梁模型，对采空后煤层峰前阶段的横向变形进行分析。计算模型如图3所示，其中，顶板厚度为H，煤层厚度为h。

图3 煤层变形计算

取顶板单元体如图4所示，定义顶板垂向挠度为ω，横截面剪力为Q，平均剪应力为τ，平均剪应变为γ，而上覆岩层对顶板的压力为q，煤层对顶板的支撑应力为p，剪切梁剪切模量为K。

图4 顶板单元体

竖向平衡公式为：

几何方程有：

物理方程有：

联立式（11）至（15）得：

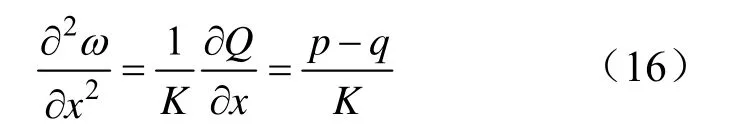
取煤层单元体如图5所示，煤层与顶板间摩擦力为τf，有平衡方程：

图5 煤层单元体

简化得：

采空后，煤层发生弹性变形，其中，在工作面附近出现弹性变形外区，此时煤层与顶板发生相对滑动，产生横向变形。而在远离工作面的区域为弹性变形外区，煤层与顶板间无相对滑动。采空区长度为a，弹性变形外区长度为B=b-a，如图6所示。

图6 煤层变形区域分布

在弹性变形内区，即b≤x，有公式：

代入平面应变公式得到弹性变形内区基本方程：

联立式（20）至式（23）得：

在弹性变形外区，即a≤x≤b，有公式：

将式（26）代入平面应变公式得到弹性变形内区基本方程：

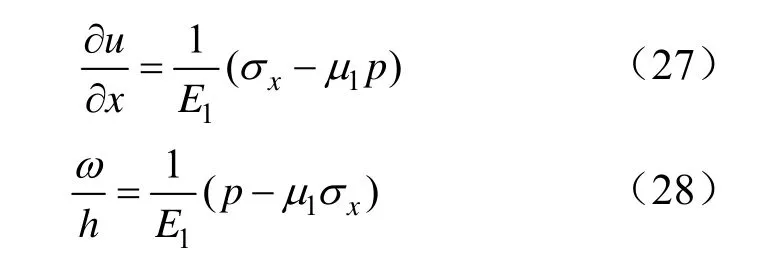
联立式（27）至式（30），得到：

解得弱夹层弹性变形外区横向变形u2：

3 中性点位置影响因素分析

下面对岩体及锚杆力学参数取值，分析不同因素对锚杆中性点位置的影响。锚杆直径db=35 mm，长度为1.5 m，杨氏模量E=210 GPa，影响范围直径d0=200 mm。煤层岩体杨氏模量为5 GPa（3 GPa、4 GPa、6 GPa），泊松比v=0.35，横向应力系数为υ=0.54（0.33，0.43，0.67），厚度h=3 m，接触面摩擦系数f=0.5。顶板剪切模量为8 GPa，厚度H=5 m，上覆岩层压力q=10 MPa。假设采空区长度a=4 m，弹性变形外区长度b=5.58 m。

3.1 煤层弹性模量的影响

图7为煤岩不同弹性模量时锚杆的应力分布。如图7所示，当煤岩弹性模量为3 GPa时，中性点在0.66 m处出现，轴应力峰值为15.5 MPa；当煤岩弹性模量为4 GPa时，中性点在0.56 m处出现，轴应力为12.0 MPa；当煤岩弹性模量为5 GPa时，中性点在0.49 m处出现，轴应力为9.9 MPa；当煤岩弹性模量为6 GPa时，中性点在0.44 m处出现，轴应力为8.4 MPa。由此可见，当煤岩弹性模量增加时，锚杆中性点到洞壁的距离减小，轴力峰值减小。

图7 煤岩不同弹性模量时锚杆的应力分布

3.2 不同横向应力系数的影响

图8为煤岩不同横向应力系数时锚杆的应力分布图。如图8所示，当煤岩横向应力系数为0.33时，中性点在0.46 m处出现，轴应力峰值为13.3 MPa；当煤岩横向应力系数为0.43时，中性点在0.47 m处出现，轴应力为11.8 MPa；煤岩横向应力系数为0.54时，中性点在0.49 m处出现，轴应力为9.9 MPa；煤岩横向应力系数为0.67时，中性点在0.51 m处出现，轴应力为7.6 MPa。由此可见，当煤岩横向应力系数增加时，锚杆中性点到洞壁的距离增大，轴力峰值减小。

图8 煤岩不同横向应力系数时锚杆的应力分布

4 结论

（1）锚杆在矩形巷道煤层中的应力分布也符合中性点理论的假设，剪力沿锚杆先减小，后改变方向增大，轴力先增大后减小；在中性点位置，剪力为零，轴力达到峰值。

（2）当煤岩弹性模量增加时，锚杆中性点到洞壁的距离减小，轴力峰值减小；当煤岩横向应力系数增加时，锚杆中性点到洞壁的距离增大，轴力峰值减小。