多变量非线性系统超平面神经网络辨识算法设计
余世明,孙云坤,岑江晖,何德峰
(浙江工业大学 信息工程学院,浙江 杭州 310023)
现实世界中大多数实际系统是非线性和时变的,无法使用线性模型精确表示。与已有的线性系统辨识方法相比,非线性系统辨识需要辨识多个未知的非线性参数以及非线性系统存在的时变和强耦合问题,最佳的辨识方案与其应用场景息息相关,因此辨识非线性系统一直是具有挑战性的问题[1]。随着人工智能的快速发展,深度学习方法在非线性系统辨识中的作用也逐渐凸显。常用的神经网络包括BP神经网络[2-3]、小波神经网络(Wavelet neural networks,WNNs)[4]、模糊神经网络(Fuzzy neural networks,FNNs)[5]、递归神经网络(Recurrent neural networks,RNNs)[6]以及连续分段线性(Continuous piecewise linear,CPWL)神经网络[7]等,上述模型已在非线性系统的辨识问题中得到了广泛应用。Pati等[4]在具有线性输出神经元的前馈神经网络中引入小波作为神经元的激活函数,以此方式将小波与神经网络相结合,促进了小波神经网络的发展。Billings等[8]提出了一种基于方差分析(ANOVA)展开的小波神经网络,将高维系统的模型构造为多个变量较少的函数的叠加,解决了中高维非线性系统的辨识问题,并在后续工作中提出了一种自适应小波网络模型[9],使用了一种两阶段混合训练方案生成一个精简的网络模型,以两个时空系统的辨识试验证明了该方法的性能。Khodabandehlou等[10]使用小波神经网络,实现了对一个通讯网络上的非线性系统的在线辨识,并将该方法应用于无人驾驶汽车的在线辨识和控制。模糊系统建模方法具有模糊推理处理不确定性的能力和灵活的规则,通过对输入和输出数据进行学习,得到精度较高的预测模型[11]。其中,模糊神经网络及其改进形式得到了广泛应用。Wu等[12]提出了一种基于数据知识的模糊神经网络(DK-FNN),使用多层连接结构,运用集成迁移学习方法和数据互相吸引策略,解决了利用不完整数据集建立准确模型的问题。以高炉炼铁过程和污水处理过程为例,证明该方法在数据集不完整时的优势。Zhang等[13]提出了一种基于自回归(ARX)与Takagi Sugeno(T-S)型的Tanh函数相结合的模糊神经网络,利用改进的遗传算法自动确定网络的结构和参数。通过对工业焦炉液位建模中的应用表明了该方法在复杂非线性系统建模中的有效性。递归神经网络中包含延时变量,能有效地处理时间序列数据[14],常用于辨识动态系统。Wang等[6]提出了一种新的递归网络FARNN,该网络由全连接的单层神经网络和反馈动态网络组成,以状态空间的形式描述未知动态系统,使用了一种完全自动化的构造算法,利用系统的输入输出数据完成对未知系统的辨识。Zhao等[15]通过一种高效的流水线功能连接人工循环神经网络(PFLARNN)进行非线性动态系统辨识,通过网络结构的模块化提高了计算效率。Zhang等[16]将递归神经网络与模糊神经网络相结合,提出了一种递归模糊神经网络(Recurrent fuzzy neural networks,RFNNs),建立了非线性系统的长期预测模型。Lin等[17]提出了一种交互式递归自进化模糊神经网络(IRSFNN),将其用于处理时变系统的辨识和时间序列的预测问题。
链接超平面(Hinging hyperplanes,HH)神经网络[18]属于一种CPWL神经网络[19],在非线性系统辨识中得到了广泛应用[20-21]。由于HH模型无法表示二维或二维以上的CPWL函数,Wang等[22]提出了广义链接超平面(Generalized hinging hyperplanes,GHH)模型,证明了该模型具有任意维度的表示能力。受多元自适应回归(Multivariate adaptive regression,MARS)[23]的启发,Xu等[24]提出自适应链接超平面(Adaptive hinging hyperplanes,AHH)模型,该模型消除了HH模型和GHH模型在辨识过程中的存在的局部最小值问题。在AHH模型之后,Xu等[25]研究了它的一种变体,高效铰链超平面(Efficient hinging hyperplanes,EHH)神经网络,与AHH相比,EHH模型更适用于高维问题。考虑到常规EHH神经网络辨识方法不能完成多变量系统的辨识,笔者使用多目标规划方法对EHH神经网络辨识方法进行改进,提出将多变量系统中各变量的辨识作为不同的优化目标,结合线性加权法和理想点法的特点,研究线性加权辨识方法和理想点辨识方法。以CFBB燃烧过程为例,分别使用线性加权辨识方法和理想点辨识方法设计CFBB建模方法,通过大量实验数据,完成对CFBB燃烧过程的辨识。
1 EHH神经网络预测模型
EHH神经网络如图1所示,它包括一个输入层、一个隐藏层和一个输出层。隐藏层结构如图2所示。图1,2中:x为输入变量;D为源节点;C为中间节点;y为输出变量。
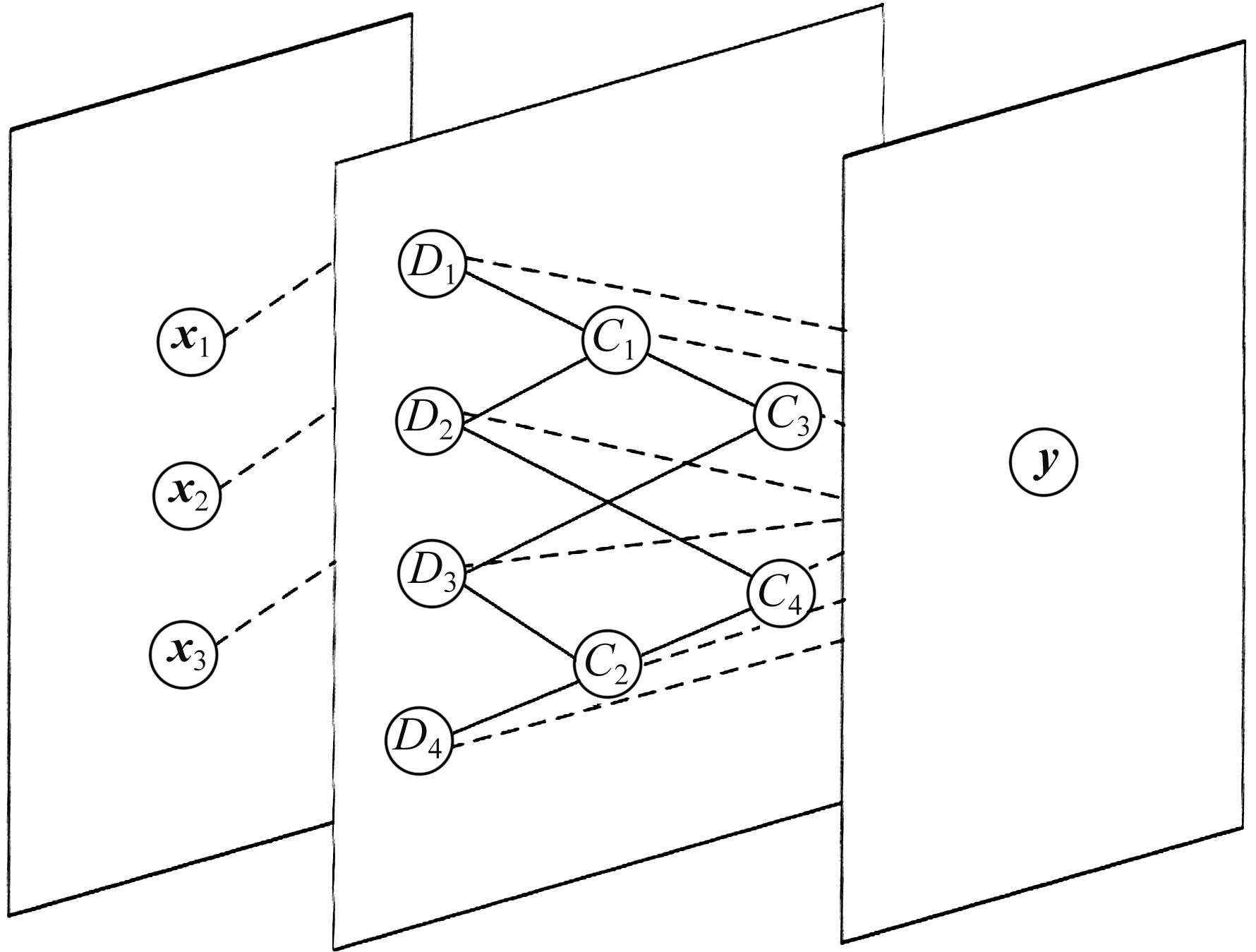
图1 EHH神经网络示意图Fig.1 The structure of a EHH neural network
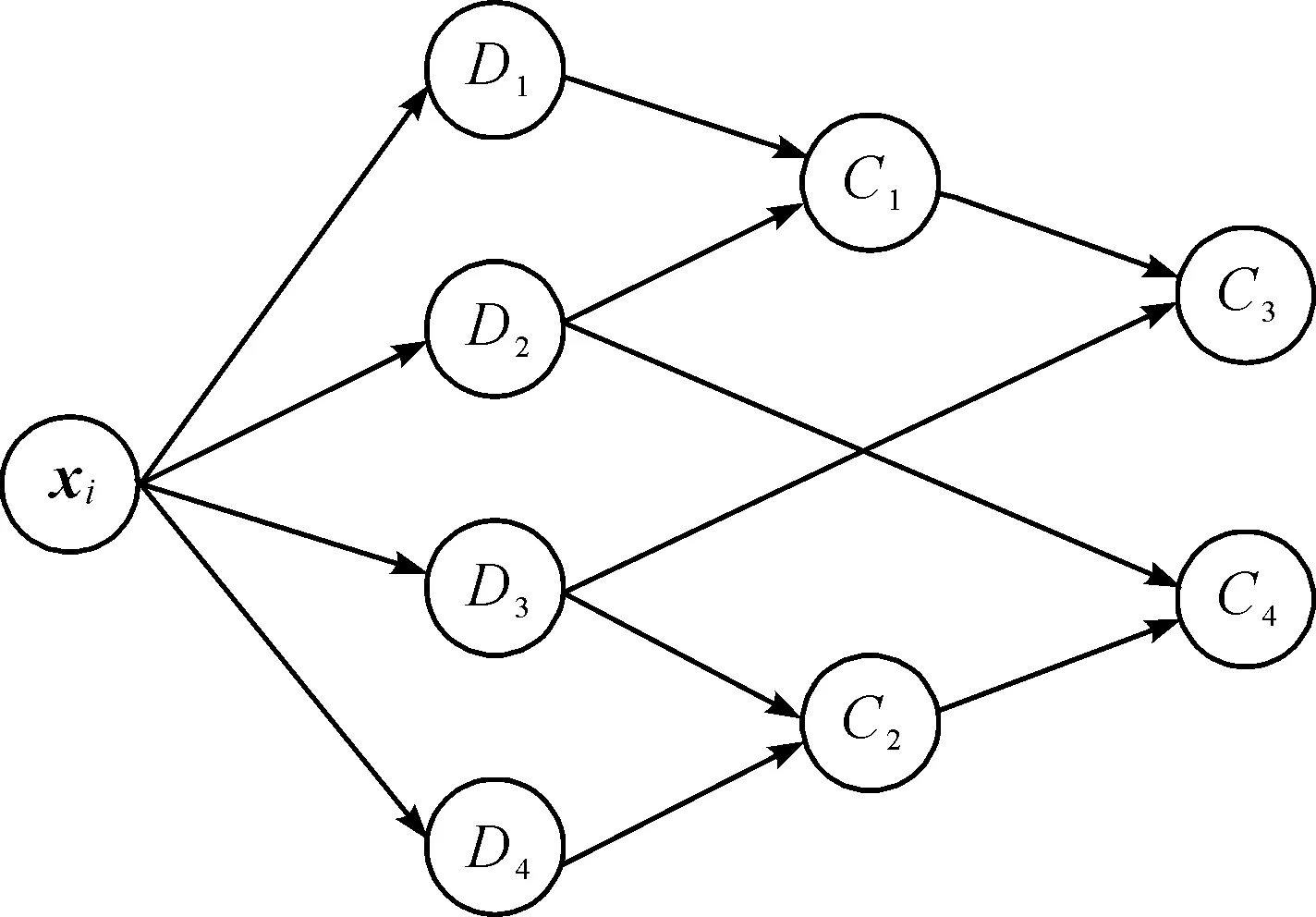
图2 隐藏层示意图Fig.2 The view of hidden layer
1.1 输入层与隐藏层的连接
在EHH神经网络中,输入层与隐藏层之间通过源节点D连接,因此定义源节点为只接受输入层输入变量传递数据的节点。源节点D通过max激活函数进行输出,表示为
nnD(x)=max{0,xv-βv}
(1)
式中:v为输入变量x的索引;βv为输入变量x对应的偏置。
1.2 隐藏层内部的连接
在隐藏层中,中间节点C按顺序生成和排序,只接受源节点或隐藏层中其他中间节点的输入。中间节点通过min激活函数从隐藏层中的另外两个节点接收输入数据。为了系统地表示隐藏层中各个节点,定义Ai=Di,i=1,2,…,Nd;Ai+Nd=Ci,i=1,2,…,Nc。假设节点Aj3接收节点Aj1和Aj2的数据,那么Aj3的输出为
nnAj3(x)=min{nnAj1(x),nnAj2(x)}
(2)
以图2所示的隐藏层为例,nnC1={nnD1,nnD2},nnC2={nnD3,nnD4},nnC3={nnC1,nnD3},nnC4={nnD2,nnC2}。
1.3 隐藏层与输出层的连接
EHH神经网络与其他神经网络的不同之处在于,EHH神经网络的源节点和中间节点都传输数据至输出层(图2)。因此,EHH神经网络的输出可以表示为
(3)
式中:Ak为隐藏层中的节点;nnAk为节点Ak的输出;αk为节点Ak对应的权重系数;α0为偏置。
2 多变量非线性超平面神经网络训练过程
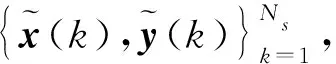
(4)
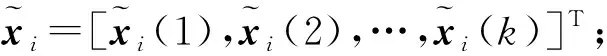
由于EHH隐藏层中所有的节点都对最后输出层产生影响,为取得较好的辨识效果,需要分别对EHH网络结构和权重参数进行优化求解。常规EHH训练方法只能求解一个EHH神经网络结构和一个对应的权重向量α,因此只适用于单变量系统模型的辨识,无法辨识多变量系统。笔者提出将多目标规划的方法与EHH神经网络训练过程相结合,完成对多变量系统的辨识。
考虑到多变量系统具有多个输出变量,需要使用一个EHH神经网络结构,通过多个权重向量分别映射不同的输出变量。因此将不同输出变量的辨识看作是不同的目标,为每个变量设计一个目标函数,通过多目标规划的方法求解各目标函数,得到优化后的网络结构以及各输出变量对应的权重向量,从而实现对多变量系统的辨识。求解多目标规划的方法有很多,考虑到EHH神经网络的特性和系统辨识的过程,使用线性加权法和理想点法进行辨识。
2.1 线性加权EHH神经网络辨识算法
线性加权法就是将各个子目标线性加权和作为评价函数,即
F(X)=γ1f1(X)+γ2f2(X)+…+γnfn(X)
(5)

(6)
假设隐藏层共有M个节点,其中源节点数量为Nd,源节点数量为Nc,对于具有n个输出变量的多变量系统,为每个输出变量设计目标函数,即
fi(αi)=(y-Zαi)T(y-Zαi)+λi‖αi‖1
(7)
式中:i为输出变量的索引值;y=[y(1),y(2),…,y(Ns)]T;αi=[αi0,αi1,…,αiM]T;Z的表达式为
(8)
收缩变量λi是为了控制权重αi的大小,其定义为
(9)
式中:lαi为权重向量αi的数量,lαi=M+1;ξi为参数,根据经验选取。结合式(5,7),建立线性加权训练方法的目标函数为
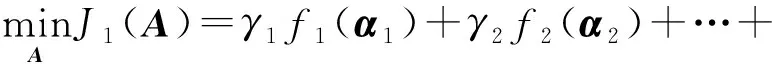
(10)
式中A=[α1α2…αn]。
2.1.1 结构优化
EHH神经网络的结构优化是指通过调整隐藏层中各中间节点的连接方式,求解出一个辨识效果最优的连接方式。使用式(10)依次对(M-Nd)个中间节点进行优化,即选取第Nd+k个节点,k=1,2,…,Nc,遍历其输出的(Nd+k-1)(Nd+k-2)/2种可能性,分别求解该情况下的目标函数值,以使目标函数值最小的连接方式作为该节点最优的连接方式,以此类推,直至完成对所有中间节点的优化,得到最优网络结构。
2.1.2 权重优化
在完成对网络结构的优化后,进行权重向量A的优化求解。固定最优网络结构保持不变,迭代求解线性加权目标函数式(10),直至J1(A)不再减小,此时求解得到的权重向量A就是该网络结构最优的权重向量。
2.2 理想点EHH神经网络辨识算法
使用EHH神经网络辨识多变量系统时,存在同一个EHH网络结构无法使得多个输出变量同时达到最优辨识效果的冲突性。为解决该冲突,使用理想点法进行辨识。

(11)
对于具有n个输出变量的多变量系统,相同的,假设隐藏层共有M个节点,其中源节点数量为Nd,源节点数量为Nc。每个输出变量的目标函数如式(7)所示。
2.2.1 结构优化
根据理想点法,每个输出变量的目标函数式(7)构造理想点评价向量为
F(A)=[f1(α1)f2(α2) …fn(αn)]
(12)

(13)
使用目标函数式(13)依次对(M-Nd)个中间节点进行优化,遍历优化所有中间节点后,得到折中网络结构。
2.2.2 权重优化

3 仿真与结果分析
以生物质循环流化床锅炉(Circulating fluidized bed boiler,CFBB)燃烧过程为研究对象,使用多变量高效链接超平面神经网络辨识方法学习生物质CFBB燃烧过程的预测模型。CFBB燃烧过程如图3所示,其过程的简要描述:给料机将生物质燃料送入炉膛底部后,燃料被炉膛底部存在的流化态的燃烧物迅速加热燃烧;随着一次风和二次风进入炉膛,质量较大的燃料在下部密相区剧烈燃烧,而质量较小的燃料则被气流夹带着进入上部稀相区燃烧。

图3 循环流化床锅炉结构示意图Fig.3 Schematic diagram of circulating fluidized bed boiler
部分稀相区的燃料先通过分离器后被收集,再由返料器送回炉膛循环燃烧,烟气经过尾部完成热交换,最后经过除尘器净化后排向大气[27]。Ikonen等[28]建立的机理模型为

(14)
式中:WC为燃烧剩余量;CB为床氧体积分数;CF为稀相区氧体积分数;TB为床温;TF为稀相区温度;PT为热功率;QC为锅炉燃料给料速率;F1为一次风风速;F2为二次风风速;其余模型参数如表1所示,具体取值见文献[28]。
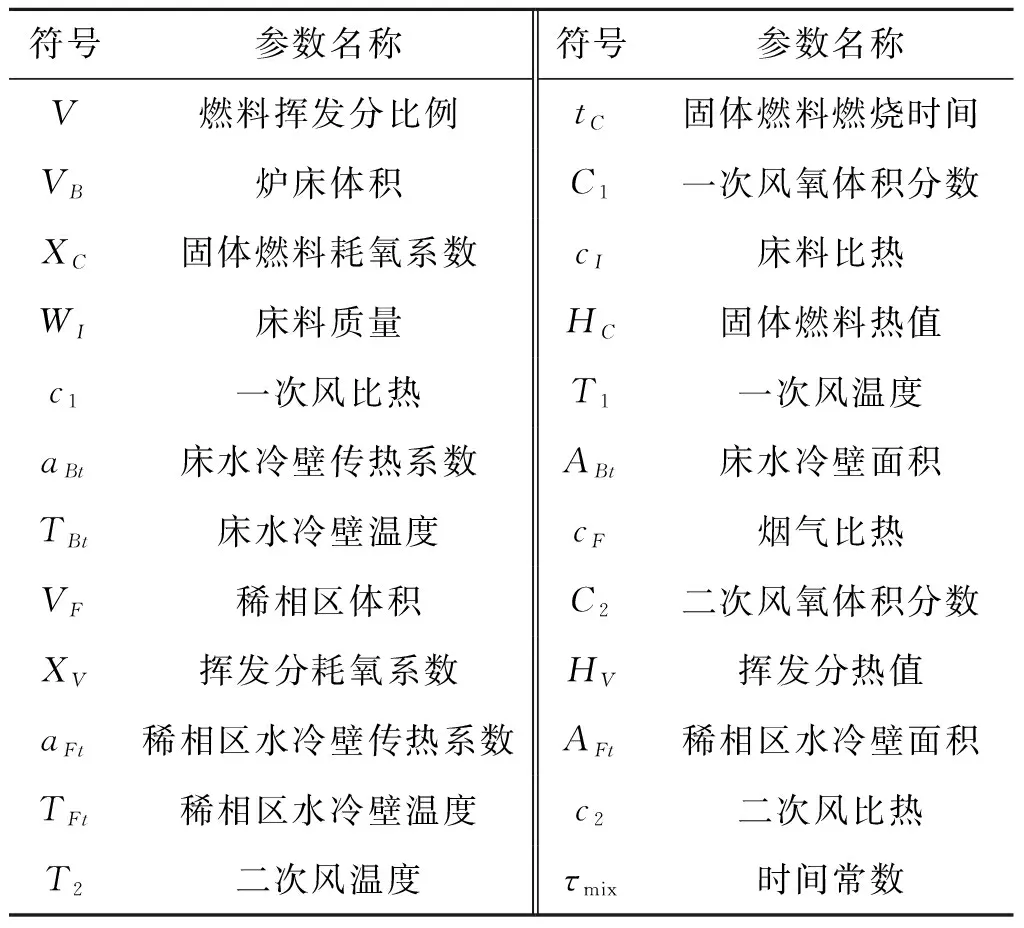
表1 CFBB模型参数Table 1 The variable of CFBB
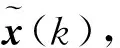
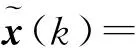
PT(k)QC(k)F1(k)F2(k)]T
(15)

TF(k+1)PT(k+1)]T
(16)
按照CFBB燃烧过程的实际情况,设置多组u(k)=[QC(k),F1(k),F2(k)]T以覆盖整个运行工况,如图4所示,其中图4(a~c)分别为QC,F1,F2的控制输入。将这些数据集应用于系统模型式(14),得到的输出数据集如图5所示,其中图5(a~f)分别为WC,CB,CF,TB,TF,PT的输出数据集。另外,设置500组数据作为预测精度的验证集。利用该训练数据集,分别使用线性加权法和理想点法对EHH神经网络进行训练。经多次试验,最终设置EHH神经网络节点数为50个,其中源节点27个。验证集的控制输入设计为
Qc(k)=3.9+0.4sin(0.05πk)F1(k)=5+0.9sin(0.13πk)F2(k)=15.1+0.6sin(0.04πk)
(17)
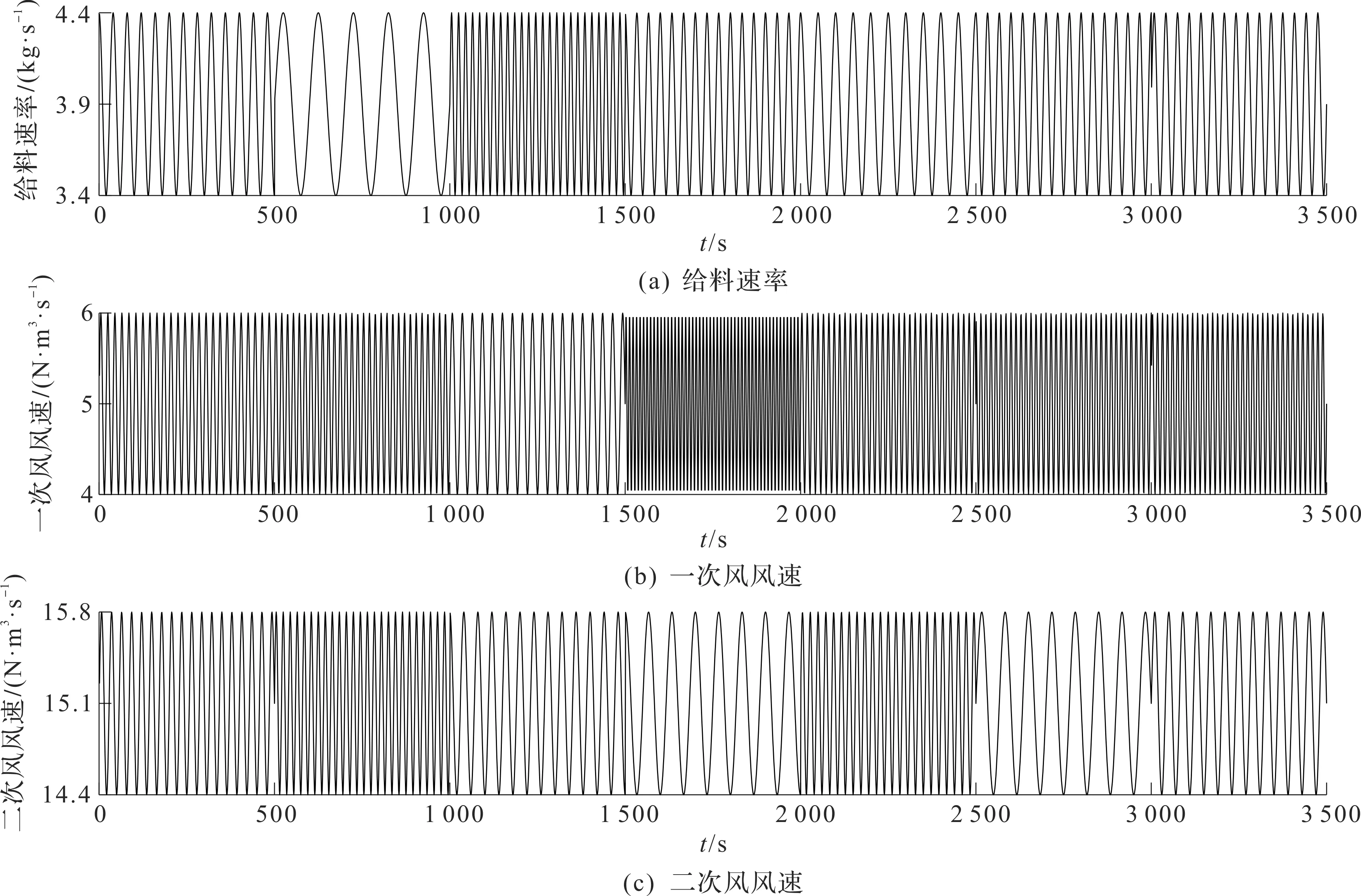
图4 控制输入Fig.4 The control input dataset

图5 输出数据集Fig.5 The output dataset
3.1 线性加权EHH神经网络辨识算法
使用线性加权法学习CFBB预测模型,由于CFBB具有6个输出状态量,所以设计6个如式(7)所示的目标函数,分别对应6个变量,构造线性加权训练方法的目标函数为
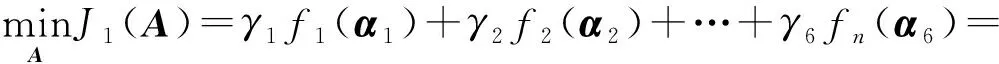
(18)
式中A=[α1α2…α6]。第1次试验设置加权系数为γ1=1,γ2=1,γ3=1,γ4=1,γ5=1,γ6=1,使用内点法进行优化问题的求解。使用验证集的数据对训练完的模型进行测试,结果如图6所示。其中图6(a~f)分别表示WC,CB,CF,TB,TF,PT的预测结果,实线表示CFBB输出的真实值,虚线表示EHH预测模型输出的预测值。由图6可知预测效果并不佳。根据各变量的预测结果,调整加权系数为γ1=3,γ2=100,γ3=100,γ4=25,γ5=1,γ6=10,使用该组数据进行训练,结果如图7所示。由图7可知:对加权系数进行适当调整,可以明显提高预测精度。
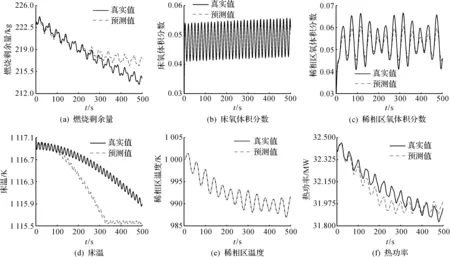
图6 第一次试验预测结果Fig.6 The prediction of first test
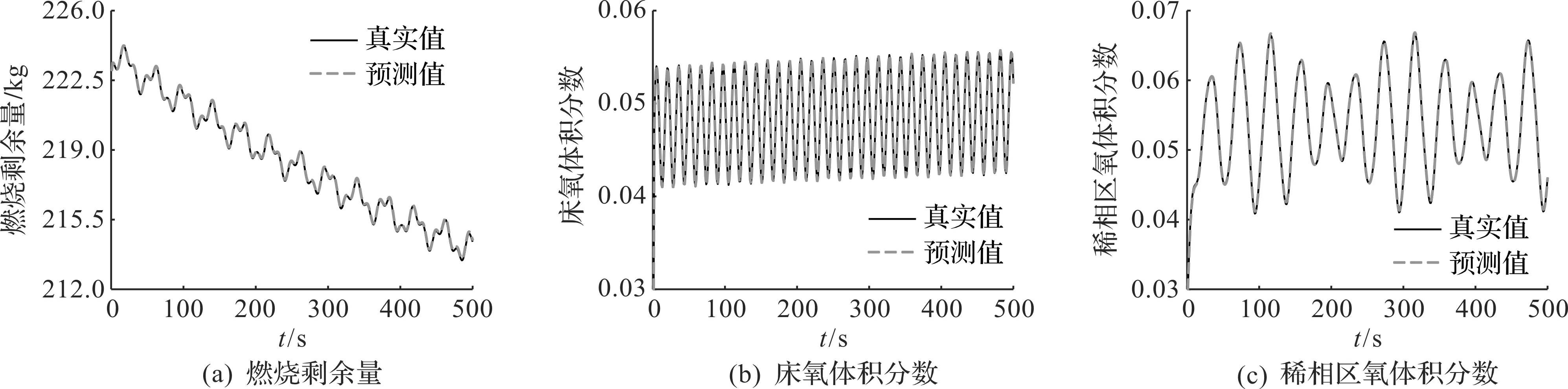

图7 调整加权系数后的预测结果Fig.7 The prediction after adjusting weighting coefficient
3.2 理想点EHH神经网络辨识算法
按照2.2节所述理想点辨识法对CFBB燃烧过程进行辨识。与线性加权法类似,设计6个如式(7)所示的子目标函数,构造评价向量为
(19)
(20)

(21)


表2 3次试验的均方根误差对比Table 2 Comparison of mean square errors of 3 experiments
4 结 论
在现有EHH神经网络学习预测模型方法的基础上,将各个输出变量的辨识作为不同的优化目标,使用线性加权法和理想点法对其训练过程进行改进,实现了对多变量系统的辨识。以复杂的生物质CFBB燃烧过程为研究对象,以大量实验数据作为训练数据集,分别以线性加权法和理想点法进行仿真试验。以仿真对比图和均方根误差作为辨识精度的评价指标,两种方法得到的CFBB预测模型均具有较高的精度。其中线性加权法需要根据经验对加权系数进行调整,才能取得较好的辨识效果,而理想点法能直接训练并得到较好的预测模型。因此,对于复杂系统的辨识,理想点训练方法更加适用。

