沿海输电导线风压数值模拟及风洞试验分析

徐 英,胡成杰,朱敏俊

(1.舟山启明电力设计院有限公司,浙江 舟山 316000;2.浙江工业大学 土木工程学院,浙江 杭州 310023; 3.浙江交工集团股份有限公司设计院分公司,浙江 杭州 310051)

风会给大跨柔性结构的稳定性带来明显影响[1-3],随着跨海交通建设工程、海岛建设工程等一系列近海工程的开展,我国沿海地区输电线路的建设工程逐渐增多,但是在架设沿海地区跨海输电线路时面临一个十分棘手的问题,即高风速下的抗风设计。研究表明:输电线路作为典型的风敏感结构,其中导线所受到的风荷载占整个输电线路风荷载的50%～70%[4],与目前输电线路中使用最为广泛的钢芯铝绞线相比,低风压导线所受的风压较小,这对于减弱风荷载的作用及提高输电线的抗风压能力意义重大。国外学者木村容康等[5]对低风压导线的机理及其应用进行了研究;Teruhiro等[6]和Toshio等[7]分别对低风压噪音架空线和低风压绝缘线进行了研究。近年,随着我国输电线路建设的不断加速,国内学者也对低风压导线展开研究。如尤传永[8]对低风压导线进行了研究,相较于普通导线,低风压导线阻力系数下降约30%;谢强等[9]和彭添等[10]借助风洞试验,对分裂导线的整体阻力系数随不同参数的变化规律进行了研究,进一步为导线振动防治提供参考;胡渊尉[11]对低风压导线机理进行分析,并对其开发应用及试验进行展望。国内部分学者[12-19]利用风洞试验对输电导线的气动参数以及导线的选型和输电线路的安全也有一定研究。针对导线气动力特性的研究,文献[20-26]利用数值模拟研究典型导线的气动力特性;沈国辉等[27]采用风洞试验对比不同风速导线和同直径圆柱的阻力系数,并与《架空输电线路杆塔结构设计技术规定》[28]的有关规范进行对比。但是,目前针对风压利用数值模拟和风洞对比展开的研究则较匮乏,风压和风荷载作为导线气动力特性的重要体现,有必要借助风洞试验对其进一步研究。此外,针对低风压导线风荷载分配系数也鲜有研究,目前在国内仍处于理论分析和假设阶段,亟需风洞试验来验证[29]。

鉴于上述研究现状,首先,基于CFD数值模拟对低风压导线周围风压分布进行初步分析;然后,考虑舟山沿海地区实际的风速,参考文献中的风速取值[12-14,17,27],借助风洞试验对具有代表性的10,20 m/s来流风速下不同方位角的低风压导线和ACSR风压变化规律进行对比分析;最后,基于10,20 m/s风速对低风压导线的分配系数进行具体分析,以期为架空输电线路杆塔结构设计技术规定[28]中不同方位角条件下分配系数的选取提供一定参考。

1 CFD数值模拟

为获得低风压导线周围风场风压分布规律,鉴于舟山地区实际风速,采用具有代表性的20 m/s来流风速,对低风压导线(直径D=38.4 mm)进行二维数值模拟。

1.1 计算域及网格划分

借助计算流体动力学软件FLUENT对图1所示的低风压导线截面进行有限元建模计算。

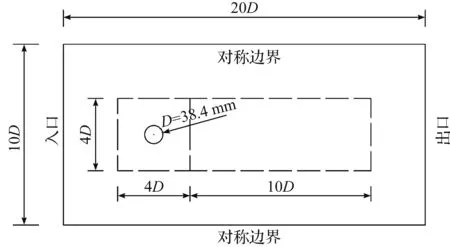
图1 计算域Fig.1 Computational domain

细长的低风压导线沿长度方向截面形状不变,各截面形式不同(即绕截面形心旋转一定角度),因此选用二维模型对其进行计算分析。在建立模型时,合理地选择计算域的大小不仅可以保证模型的精确性,还能将边界对流场的影响降到最低,更能缩短分析计算时间、提高计算精度。考虑风洞试验阻塞率不能大于5%的要求,计算域长度取20D(低风压导线外径D=38.4 mm),宽度取10D,对整个计算域划分为3个区块(图1),内部两个区块面积分别为4D×4D,4D×10D(图1),靠近导线附近的区块网格适当加密,外围区块的网格适当稀疏,使网格由导线向四周有逐渐变稀疏的趋势,以便更准确地模拟实际风场情况,并可让导线背部尾流充分发展。计算域的整体网格划分如图2(a)所示,导线周围局部网格如图2(b)所示。

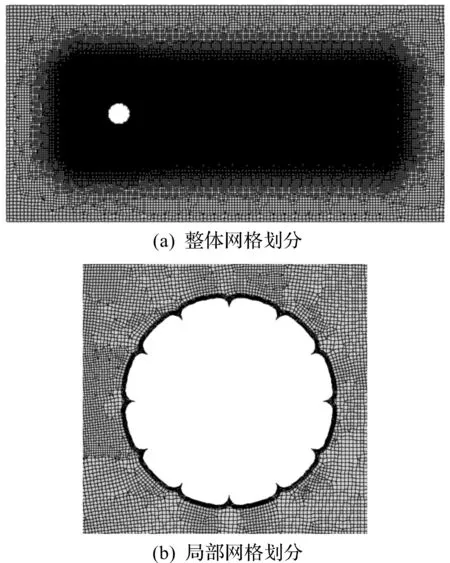
图2 计算域网格划分Fig.2 Grid generation of computing domain

1.2 计算设置

将建立的有限元网格模型导入FLUENT进行计算,风场入口(Inlet)采用速度入口,风速为20 m/s,以保证整个流场的均匀来流;风场出口(Outlet)采用Outflow出口,以保证尾部气流的自然流出,避免了尾部气流回流给模拟带来的影响;上下边界采用对称边界(Symmetry),等同于自由滑移的壁面,以保证该边界法向速度等物理量梯度为0,从而避免对来流的影响,更真实地模拟导线上下两侧远方的空气流动几乎不受影响的实际情况;低风压导线表面设置为无滑移壁面(Wall)。

模拟选用SSTk-ω模型,采用有限体积法进行离散,速度与压力耦合采用SIMPLE算法,并采用二阶迎风格式离散。根据网格划分原理,选用非结构化网格,在导线附近区域进行了非结构网格加密处理,导线外围及尾流发展区网格适当稀疏。边界层为6层,以1.1的增长率向外扩张。为保证精度,接近边界层的网格y+值小于1,收敛残差都控制在10-3以下。

1.3 数值模拟结果分析

流场中导线绕流的风场压力整体云图如图3(a)所示,局部细节图如图3(b)所示。

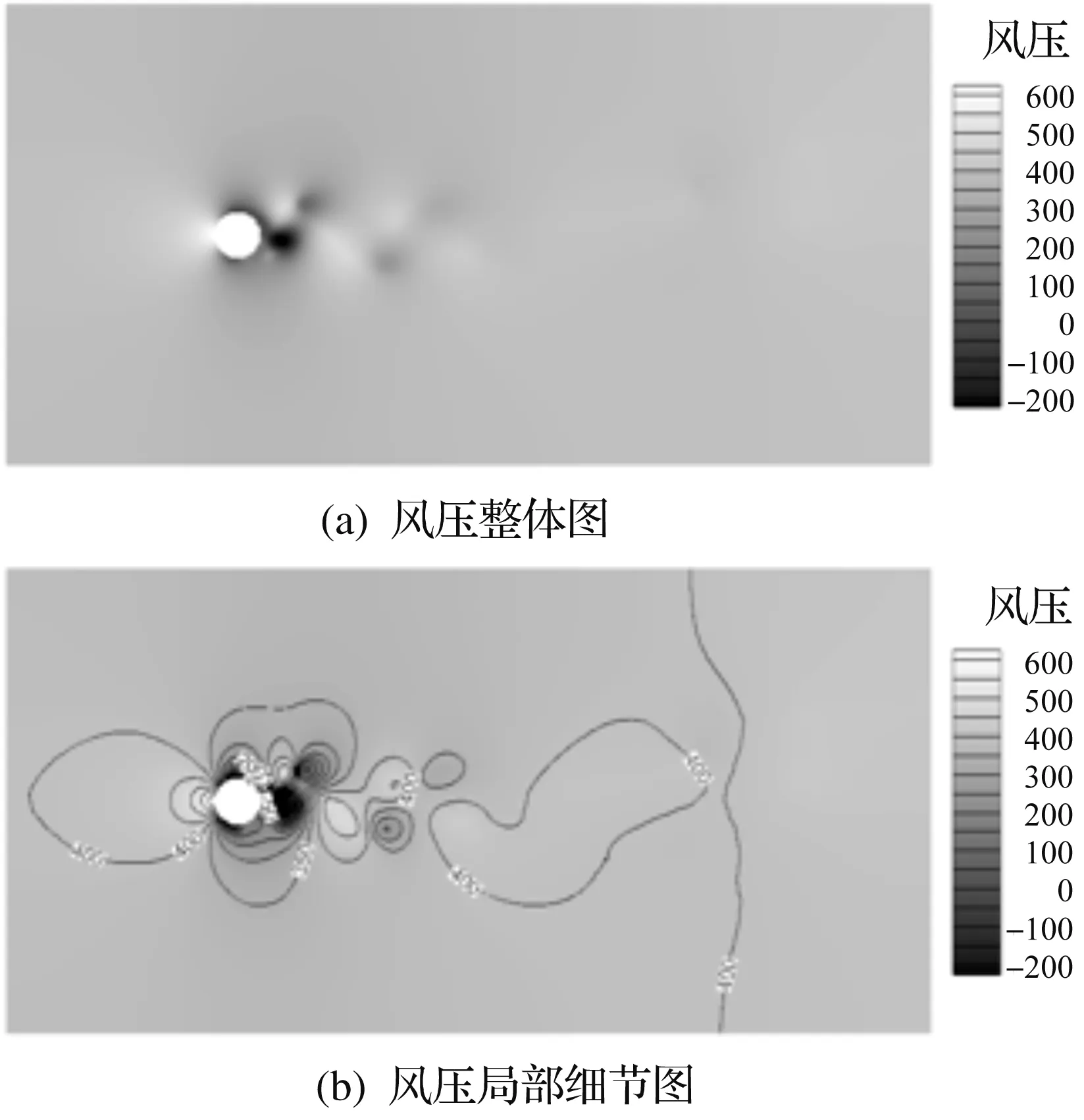
图3 风压云图(单位:Pa)Fig.3 Wind pressure cloud picture (unit: Pa)

由图3(a,b)可知:风压在计算域内的分布差异明显,在来流作用下导线周围风压分布具有一定的规律性,导线迎风侧表现为正压,背风侧表现为负压,在导线周围有负压区的存在。在导线的两侧也可以明显发现风压分布情况近似成对称分布,两侧风压小于迎风侧风压。总体来看,导线尾流区域压强较小,该区域长度约为导线外径的两倍,区域湍动现象明显。导线前后压强差在150 Pa左右,150 Pa压强差转换为力,体现在力上约4.032 N,与20 m/s风速下的风洞实测数据3.887 8 N非常接近,误差为3.7%。总体而言,低风压导线的绕流现象与传统的圆柱绕流类似,有明显的气压差和涡脱现象。数值模拟导线绕流的风速整体云图如图4(a)所示,局部细节图如图4(b)所示。

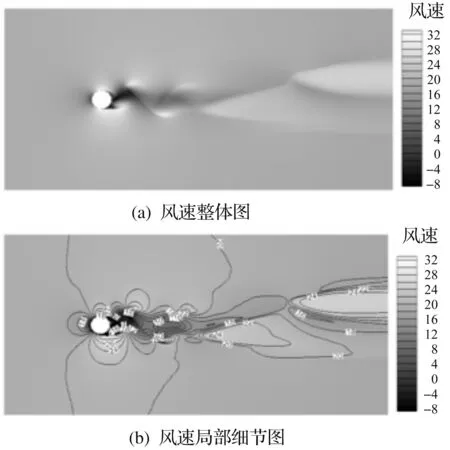
图4 风速云图(单位:m/s)Fig.4 Wind velocity cloud picture (unit: m/s)

由图4(a,b)可知:由于导线的遮挡作用,导线迎风侧风速较小;导线上下侧风速较大,最大值接近30 m/s;导线背风侧的风速较小,在导线迎风侧,气流受到导线的阻挡,在紊流风速情况下,导线两侧近似不对称分布。在导线表面,受到来流风速的影响,气流沿着导线向两侧流动,从而导线侧面速度加大,在尾部风场速度变化成旋涡脱离。

2 风洞试验

为研究低风压导线与普通钢芯铝绞线所受风压的差别,开展了风洞试验以进行对比分析。风洞试验段截面尺寸为4 m(宽)×2.8 m(高),测力天平段最高风速为20 m/s。导线所受阻力采用高频动态测力天平(HFFB)测得。采用如图5,6所示的低风压导线和钢芯铝绞线截面图进行试验模型制作,导线模型材料采用玻璃钢(FRP),因其密度低、重量轻和强度高的特点能够避免过高风速对模型形状造成影响,较好地满足了风洞试验的要求。两种导线的参数如表1所示。

图5 低风压导线Fig.5 Low wind pressure conductor

图6 钢芯铝绞线Fig.6 ACSR

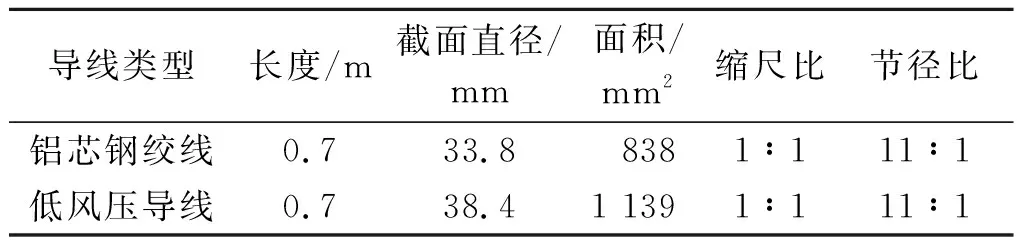
表1 导线参数Table 1 Conductor parameters

为研究两种风速工况下360°全方位角风荷载作用下导线风压分布规律,将导线沿来流方向定义为0°,如图7(a)所示,将导线垂直于来流方向定义为90°,如图7(b)所示,并分别在0～90°以15°为间隔定义7个风向工况(0°,15°,30°,45°,60°,75°,90°),然后进行10,20 m/s均匀流风吹试验,以获得导线风压力数据。考虑到风洞内受近地面的影响,沿竖向高度方向无法保证完全均匀流,因此采用将导线横向放置的测试方法,将导线固定于支架,如图7(c)所示。实际操作中,首先将导线置于支架上,测得导线和支架的总阻力;然后撤去导线,测得空支架所受阻力,两者的差即为导线所受阻力。

图7 导线方位角示意图Fig.7 Schematic diagram of conductor azimuth

3 两导线风压结果对比分析

根据文献[30],把风速V按图8正交分解可得

Vx=V×sinθ

(1)

Vy=V×cosθ

(2)

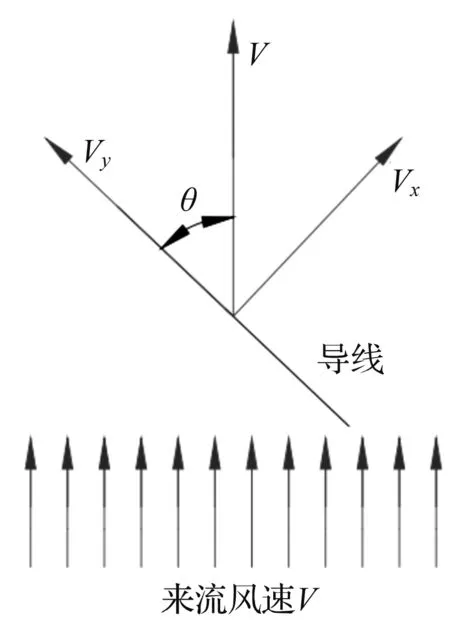
图8 风速分解示意图Fig.8 Wind speed decomposition diagram

与风速分解一样,风荷载F同样可以分解为垂直导线方向和顺导线方向的风荷载(Fx,Fy),进而通过迎风投影面积转换为等效风压(px,py),来定量研究不同方位角的风压分布规律。不同方位角由测力天平测得的荷载分布情况如图9所示,由荷载转化而来的风压分布情况如图10所示。由图9可知:与钢芯铝绞线相比,低风压导线在两种风速条件下,所受的风荷载均较小,且风速越大所受的风荷载差距越大。进一步观察0°和90°方位角所受风荷载,0°情况下,垂直导线方向荷载接近0,此时顺导线方向荷载最大,与实际情况相符合;90°情况下,此时垂直导线方向的荷载最大,相应的顺导线方向风荷载却不为0,这可能是由于风场的三维湍流造成的,三维湍流在导线两端会带来局部效应,使得局部风荷载较大,从而与理论值0有所出入,若架设导线为无限长,则与理论值0会较为接近。30°方位角处的荷载较特别,小于30°时,低风压导线和普通的钢芯铝绞线所示荷载差别不大;大于30°时,两种导线所受荷载差别较大。

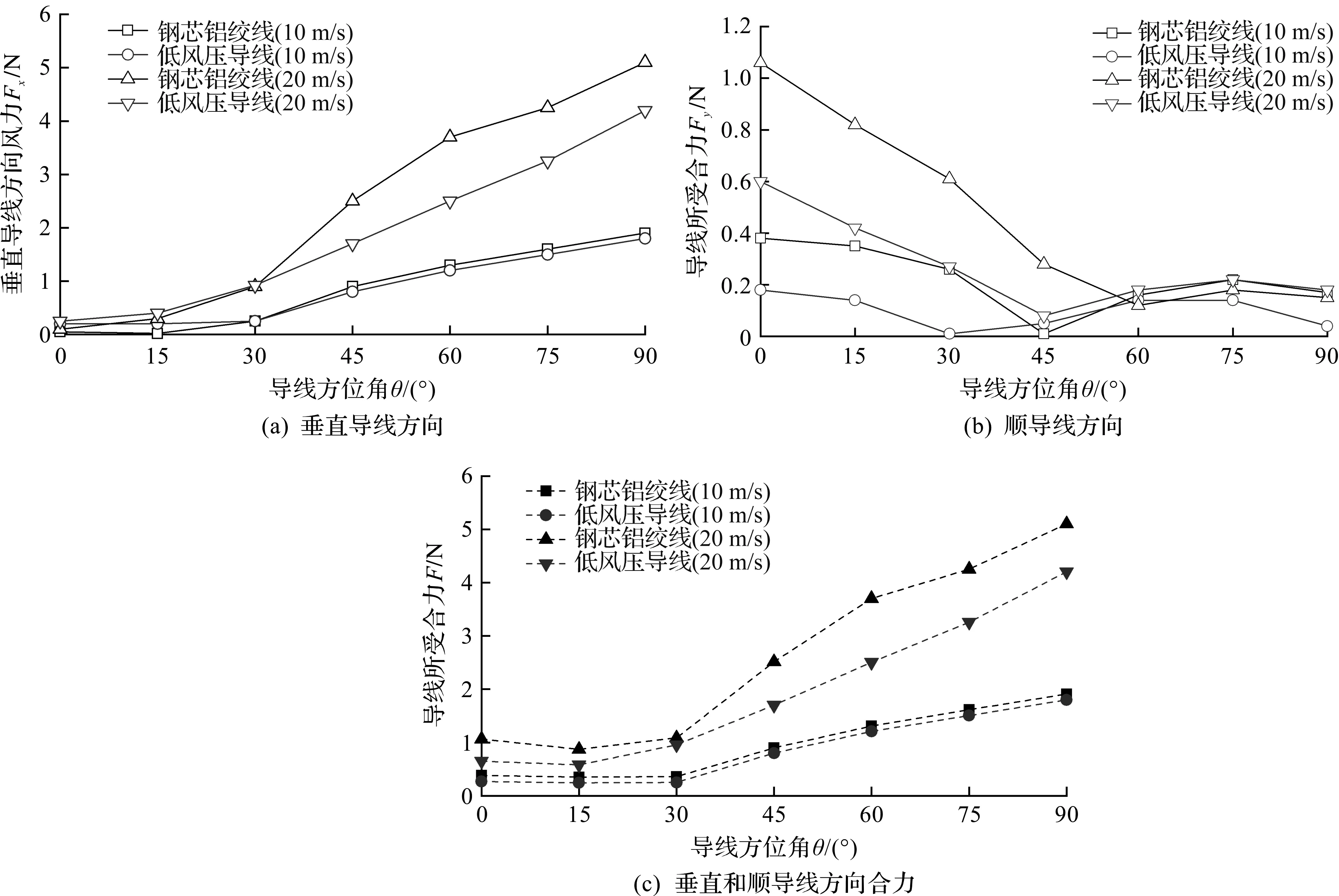
图9 不同方位角的荷载分布Fig.9 Load distribution under different azimuth

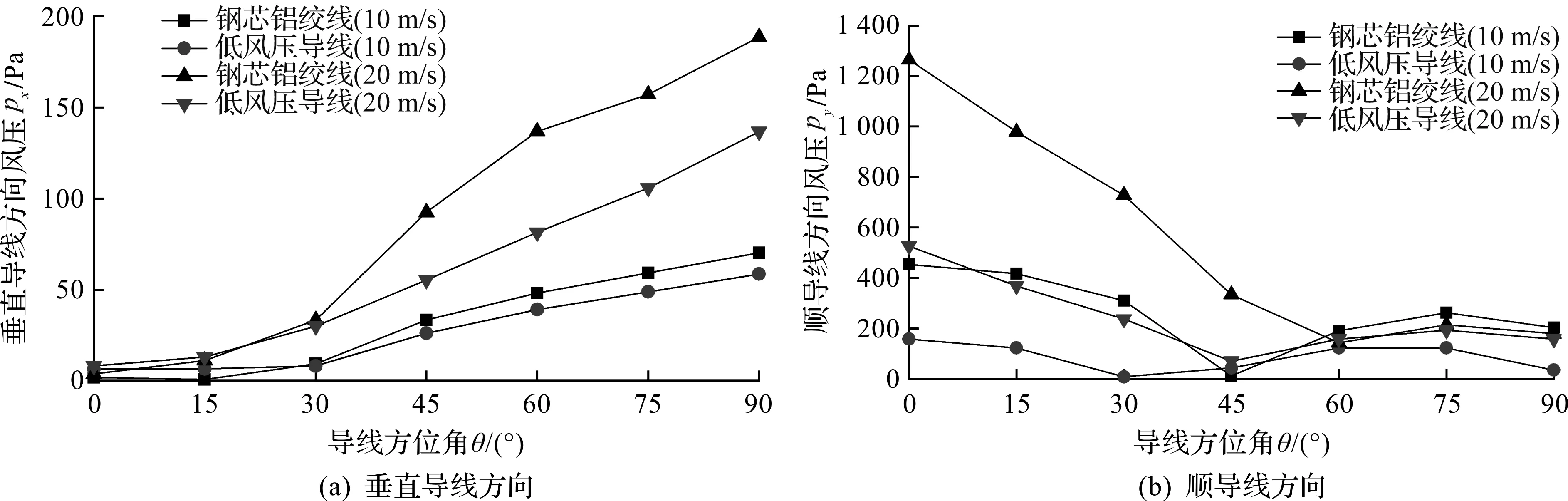
图10 不同方位角的风压分布Fig.10 Wind pressure distribution under different azimuths

风压p定义为单位面积上所受风荷载的大小,由于低风压导线和普通钢芯铝绞线的截面面积不同,在风洞试验中同一方位角条件下两者的迎风面面积有差别,为更好地进行对比分析引入风压的分布情况。

图10与图9所示的变化规律趋势一致,低风压导线所受风压较小,风压在垂直导线方向最优能降低28.6%,在顺导线方向最优能降低34%左右。

4 低风压导线风荷载分配系数研究

考虑低风压导线较铝钢芯铝绞线在降低风压上的优势,选取低风压导线来研究不同风向角下的风荷载分配系数,并结合风洞试验来考虑风荷载的修正,以期为规范提供一定参考。

当风向与导线方向不垂直时,风荷载会分解为垂直导线方向和顺导线方向两个分量的荷载,这两个方向的荷载与风向垂直导线时的荷载之比即为导线的风荷载分配系数。根据《架空输电线路杆塔结构设计技术规定》[28],不同风向作用下的线条风荷载取值如表2所示。

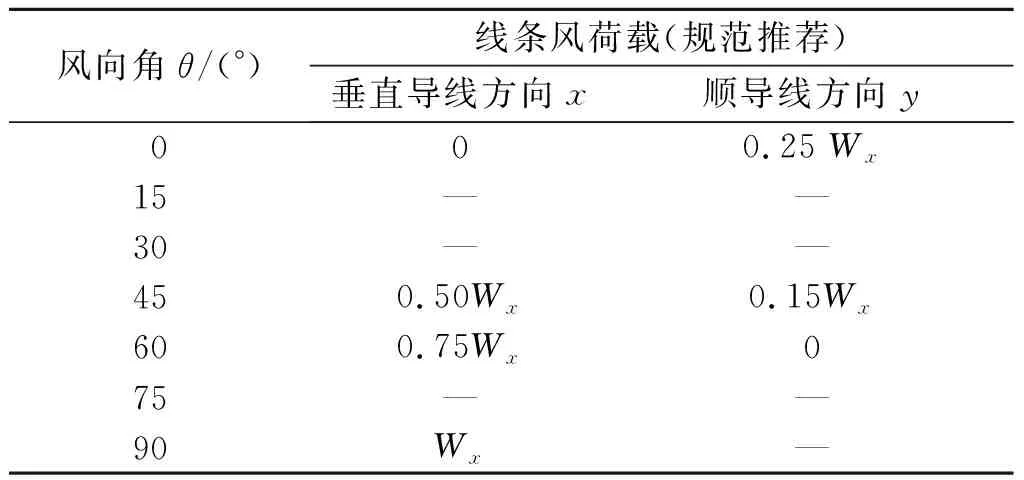
表2 不同角度风的风荷载Wx分配表

图7所示的节段模型周边的三维风场效应将导致顺导线方向下的分配系数存在一定的偏差(低风压导线表面存在一定摩阻),因此需要对风洞试验中顺导线下的风荷载分配系数进行修正。根据风洞试验数据,不同风速(10,20 m/s)低风压导线风荷载分配系数如图11,12所示。

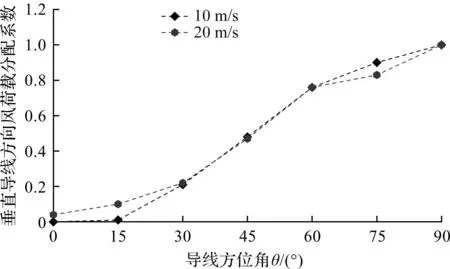
图11 低风压导线垂直导线方向风荷载分配系数Fig.11 Distribution coefficient of wind load in vertical direction of low wind pressure conductor

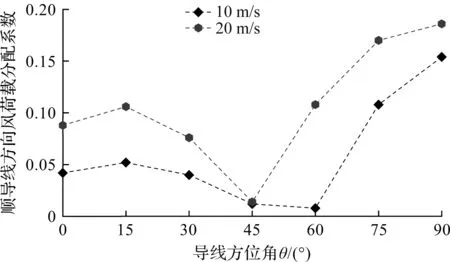
图12 低风压导线顺导线方向风荷载分配系数Fig.12 Distribution coefficient of wind load along low wind pressure conductor

垂直导线方向和顺导线方向的风荷载计算公式为

W垂直=Wx·sin2θ

(3)

W顺=0.25·Wx·cos2θ

(4)

根据顺导线方向的风荷载体型系数理论计算和规范,结合风洞试验的结果,修正后的低风压导线风荷载分配系数如表3所示。

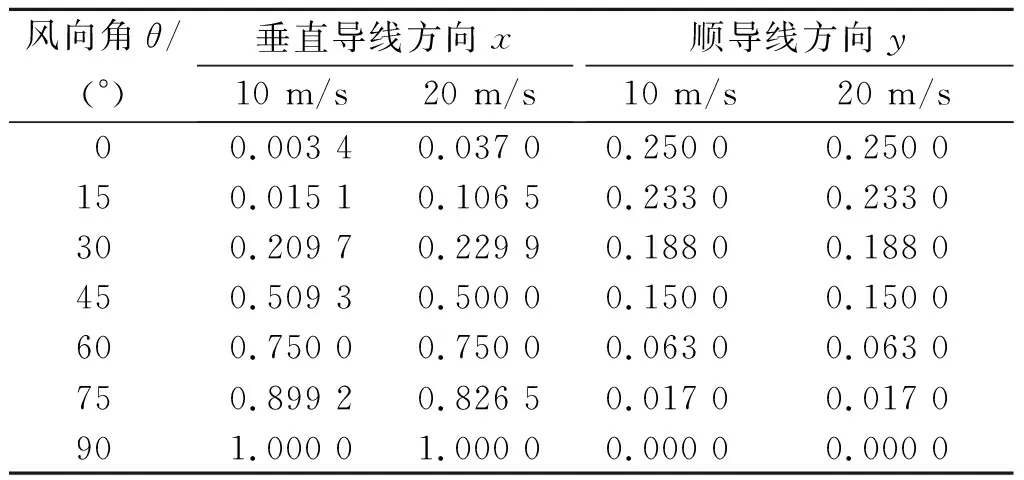
表3 不同角度风的低风压导线修正后风荷载分配系数

由表3可知:低风压导线在垂直导线方向的风荷载分配系数数随风向角的增大而增大,在90°风向角时达到最大值。在0°,15°,30°风向角下,10,20m/s两种风速的分配系数差别较大;而在45°,60°,75°,90°风向角下,10,20 m/s两种风速所得风荷载分配系数十分接近。

5 结 论

针对低风压导线的局部风场开展数值模拟研究,并对低风压导线和普通钢芯铝绞线在不同方位角以及两种风速下(10,20 m/s)的风场开展风洞试验研究。研究结果表明:数值模拟能较好地反映90°方位角下低风压导线周围的风压分布规律,模拟的风压与风洞试验所得风压较接近,误差为3.7%,与普通钢芯铝绞线相比,低风压导线能有效降低风压,降低效率在30%左右;30°方位角处的荷载情况较特殊,小于30°时,低风压导线和普通的钢芯铝绞线所示荷载差别不大,大于30°时,两种导线所受荷载差别较大,风压变化规律与风荷载一致;低风压导线在垂直导线向风荷载分配系数数随风向角的增大而增大,在0°,15°,30°风向角情况下,两种风速下(10,20 m/s)的分配系数差别较大,而在45°,60°,75°,90°风向角下,两种风速所得风荷载分配系数十分接近。同时,研究提供了15°,30°,75°这3个风向角下规范中无法确定的分配系数,不仅在一定程度上弥补了规范中存在的不足,也为工程建设中普通输电导线在不同方位角下的风压、风荷载分布以及风荷载分配系数提供一定的参考。