针对椭圆形隧道底部的横断面分割及滤波

牛晓洁 季 民 徐 飞

(1. 山东科技大学 测绘与空间信息学院, 山东 青岛 266590;2. 福州市勘测院, 福建 福州 350000)

0 引言

隧道是国家现代化建设的重要组成部分之一,由于隧道在施工及运营过程中,受附近林木、山体、人造建筑物等的影响会产生一定的变形,进而对隧道安全产生不利影响,因此对隧道进行定期检查、测量、维修是隧道工程施工运营中的必不缺少的工作。隧道断面变形的传统方法主要使用全站仪、断面仪、经纬仪等工具,虽有较高的测量精度,但测量工作时间长、断面数据少、测量效率低、且隧道内部环境恶劣时测量人员的危险性较高。近二十年来地面激光扫描技术得到了迅猛发展,地面激光扫描技术被广泛应用于桥梁、古建筑、城市街景等的三维测量工作中。相比于传统测量手段,地面激光扫描技术具有高效率、高断面点密度、断面数据量多、测量范围大、成果用途广泛的特点。

目前,针对三维激光点云的隧道横断面提取、变形分析的方法已经有了较为充足的发展,国内外诸多学者在该方面进行了深入研究。

托雷等人[1]提出一种双向投影提取中轴线的方法,即将圆形地铁隧道点云旋转使隧道法向与Y轴正交,然后将点云分别投影至XOY、YOZ平面结合随机抽样一致算法(random sample consensus,RANSAC)提取出两平面内的中线,然后通过两条平面曲线来表述空间曲线从而对隧道横断面进行提取。朱宁宁等人[2]使用双向投影的方式提取出隧道中轴线,然后依据中轴线提取隧道横断面,最后使用椭圆模型对隧道进行横断面进行拟合及滤波。程效军等人[3]通过对隧道点云双向投影获取隧道在XOY、YOZ平面的姿态变化,使用多项式方程对两条平面曲线进行拟合并插值,然后计算各中轴点的法平面以对隧道点云进行分割,最后计算各切片内的点云到中轴线的距离,使用给定的距离阈值以对隧道内部的点云噪声进行滤除。卢小平等人[4]使用双向投影的方法提取出隧道中轴线,然后依据中轴线提取隧道横断面切片,接着对横断面点云进行旋转使法线平行于Y轴,然后使用椭圆柱模型对横断面进行拟合及滤波。蓝秋萍等人[5]在隧道点云上建立高斯球,选取高斯球上的最大圆作为隧道横断面,使用最小二乘法对大圆进行拟合将最大圆所在的平面的法向量作为隧道中线;然后根据隧道中线提取横断面并提取特征线。陈林等人[6]针对盾构隧道首先使用基于距离差特征的方法识别并提取出环片连接处的环缝点云,接着对环缝点云进行最小二乘拟合;然后将环片两端的环缝曲线中心连接作为隧道中轴线。杜荣武等人[7]使用移动三维激光扫描系统对地铁进行扫描工作,根据以隧道轨迹作为基准对隧道樱花断面进行截取,然后对横断面离散点云进行拟合并与隧道设计半径相比较从而对隧道管片错台、净空收敛等进行计算。徐飞等人[8]根据隧道边界特征提取水平边界并提取出水平中线并以此提取出隧道横断面,然后对横断面进行拟合及滤波,最后结合隧道设计参数对隧道变形量进行可视化分析。赵亚波等人[9]使用移动三维激光扫描系统对盾构隧道进行测量作业,使用三维激光点云生成正射影像,根据影像中的环片点云信息计算每一环片的错台量。林景峰等人[10]使用Delaunay三角网提取隧道水平边界进而提取水平中线并以此提取横断面,然后拟合出空间中轴线。王鑫等人[11]使用三维激光扫描仪对对盾构隧道进行扫描作业,提取出隧道中线及横断面并与全站仪数据进行对比分析验证了其精度。

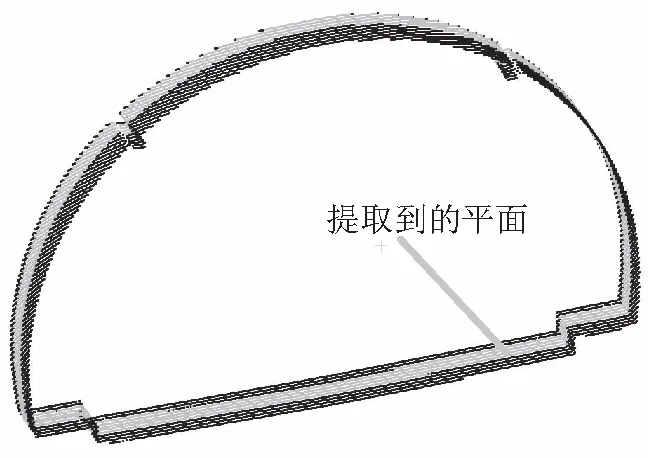
以上文献对隧道的横断面提取进行了较为深入的研究,然而目前的学者专家主要是使用规则的圆形、椭圆形、圆柱形模型对隧道进行研究和分析;然而除一些盾构隧道外,隧道并非绝对圆形,且隧道衬砌施工后往往隧道底部已不再属于圆形,如图1所示,如不对隧道底部进行精细化直接进行椭圆、圆柱拟合的话误差往往较大,因此对隧道底部点云进行精细处理是有必要的。本文提出一种针对隧道底部为矩形的隧道横断面提取及滤波方法,该方法首先将隧道点云进行XOY平面投影从而提取出水平中线,接着使用水平中线提取出隧道点云切片,然后使用RANSAC算法结合平面约束模型对隧道底部点云进行滤波分离,从而实现半圆形半矩形隧道横断面的圆形部分与矩形部分的分割,最后对圆形隧道横断面的拟合及滤波。

图1 隧道点云

1 理论方法

1.1 隧道腰部中线提取

本文提出一种先依据隧道底部特征提取隧道中轴线的方法,如图2所示,隧道底部平面与隧道壁面往往形成略大于90°的夹角α、约等于90°的β、γ。而在隧道顶部及中部位置,则不存在这一特征,因此可以利用这一特征提取隧道底部边界线。

图2 隧道底部示意图

首先将隧道点云进行旋转使轴向方向与Y轴平行,如图3所示。

图3 点云旋转俯视图

旋转公式如式(1)所示,式中(X,Y,Z)1为拟合坐标系中的点的三维坐标,(X,Y,Z)0为原始坐标系中的点的三维坐标,Rω为旋转矩阵。

(1)

随机选取种子点,以种子点为原点,Y轴方向为基准,建立局部空间直角坐标系,如图4所示,此时以种子点为圆心建立kd树,计算种子点R邻域内的点云在XOZ平面内所形成的夹角,若该角度约等于阈值α,则该点作为合格点提取出来,若该角度与阈值α相差较多,则认为该点为非合格点。遍历所有点云,提取出所有合格点即可提取边界线。

图4 隧道腰部边界线提取示意图

获取边界AB与CD的点云之后,即可获取AB与CD的中线EF,此时的EF与隧道走向相同,因此可将EF作为隧道中轴线并使用多项式方程(2)进行最小二乘拟合,作为提取隧道横断面的基准线，

(2)

式中，a为二次项系数；b为一次项系数；c为常数；x为多项式自变量。

1.2 隧道横断面提取

横断面是隧道形变分析、超欠挖分析、开挖控制、混凝土厚度控制、侵界检测、错台检测、断面间体积计算等作业的重要参考,因此对隧道横断面进行提取是隧道工程中必不可少的工作。

获得隧道中轴线后可依据中轴线为基准对隧道横断面进行分割。如图5所示,以中轴线上一点G为基准建立切向量τ,再建立切向量法平面ψ作为切割隧道的基准线,将ψ前后厚度为d/2的点云进行切割从而获得隧道点云切片,d为切片厚度。

图5 隧道切割示意图

获取点云切片后,由于隧道底部点云呈平面特征,上半部点云呈圆柱特征,因此使用RANSAC算法对平面进行检核,从而对隧道底部点云进行分割。传统RANSAC检测点云平面时首先从点云切片中随机选取三个点并进行平面模型拟合;然后计算其余点到平面模型的距离li与设定阈值λ进行比较,若li小于阈值,则认为该距离对应的点为平面点,反之则认为是非平面点;设置迭代次数n,对所有点云进行随机抽取并迭代计算,选取出最佳模型作为最终平面模型。

若直接使用传统RANSAC方法进行检测,则平面模型的选取仅依靠随机选取的点云与平面厚度即阈值λ来决定;这就导致在平面检核过程中检核出的平面并非底部平面点云,而是符合最佳模型的“类平面点云”。

为避免这一现象,本文加入平面法向量约束对RANSAC算法进行改进,具体步骤如下：

(1)从点云切片中随机选取三个点构建函数模型为

(3)

(2)计算各点li与设定阈值λ进行比较,判断模型优劣;

(3)使用最小二乘原理对阈值λ内的模型点云进行拟合,求取法向量τ(υ,ω,ξ)；

(4)计算各点云至平面函数模型Ax+By+Cz+D=0的向量(ai,bi,ci);

(5)对比计算各向量(ai,bi,ci)与法向量(A′,B′,C′)的夹角μi,若μi的数值大于设定阈值μ0,则该平面模型内的点云为符合最佳模型的“类平面点云”;反之则该平面模型内的点云为底部平面点云。以此实现对隧道底部点云的分割。

获得隧道切片后(图6)，将切片内的点云Gi(X,Y,Z)向平面ψ进行投影,得到投影点Qi(X′,Y′,Z′),从而获得隧道横断面轮廓线。

图6 隧道切片投影示意图

1.3 横断面拟合及滤波

获得剔除底部点云的隧道横断面轮廓线后,即可使用椭圆模型对隧道横断面进行拟合。本文使用间接平差对对椭圆标准方程进行拟合。首先使用对横断面进行坐标旋转使横断面轮廓线平行于XOZ平面,将三维点云转化为二维点云从而使用椭圆模型进行拟合。具体步骤如下：

(1)建立间接平差函数模型为

(4)

式中，(x0,y0)，a，b分别代表椭圆几何中心，长半轴，短半轴；xi,yi分别表示点云在平面ψ的横、纵坐标。

(2)转化为误差方程式为

(5)

根据泰勒公式将方程线性化为

(6)

式中

式中，(x0,y0)，a0，b0分别为参数椭圆几何中心坐标、长半轴、短半轴的初值；Δx，Δy，Δa，Δb为各参数增量。将式(5)转化为误差方程的矩阵形式为

(9)

式中

(10)

根据最小二乘原理,将二倍中误差2σ作为横断面滤波的参数,即若横断面点至拟合椭圆曲线的误差vi>2σ时将该点作为噪点进行滤除;反之,则将该点作为合格点保留并重新进行椭圆曲线的最小二乘拟合,直至椭圆参数的改正值Δx,Δy,Δa,Δb趋于收敛。然后将滤波后的点云逆向旋转至原始坐标系中,旋转公式为

(11)

3 实验分析

使用FARO X130三维扫描仪对某隧道进行扫描作业,隧道内壁半径RS为5.5 m。扫描仪垂直分辨率为0.009°,水平分辨率为0.009°,扫描最远距离为130 m。选取130 m隧道作为实验区,得到隧道点云1 900 553个。在VC++环境下使用文中方法对隧道进行横断面提取及拟合。

3.1 隧道边界及中线提取

首先对隧道进行预处理得到符合实验要求的隧道点云,接着根据隧道底部边界特征对隧道底部边界进行提取,如图7所示,共得到边界点云8 153个。

图7 隧道腰部边界及中线

接着遍历两条边界点,依据中点公式(12)求取中线点,式中(xleft,yleft,zleft)、(xright,yright,zright)分别表示两边的边界点坐标,(xmid,ymid,zmid)表示中线点坐标。

(12)

求取中线如图7所示,得到中线共有4 030个点,然后使用多项式方程对中线进行最小二乘拟合。由于该中线为三维曲线难以检核,因此本文使用设计桩点的二维数据进行精度检核,获得中线对比数据如表1所示。

表1 中线坐标对比

从表1中可观察到ΔX、ΔY最大值为11 mm、最小值分别为5 mm和2 mm,ΔD最大值为14.9 mm、最小值为8.6 mm,中线提取精度较高。拟合后的中线即可作为提取隧道横断面的基准线。

3.2 隧道横断面分割及拟合

3.2.1 横断面分割

提取并拟合出隧道中线后,以此为基准构建横断面方程,切割横断面切片,本文设置横断面切片厚度为0.15 m,共有650个横断面切片,切片厚度与中线点间隔一致为0.15 m。由于横断面切片互相连接不宜展示,为便于展示,本文实验部分采用间隔4 m,切片厚度为0.11 m的横断面数据进行展示,如图8所示为隧道切片。

图8 横断面切片

获得点云切片后,传统方法往往直接使用RANSAC算法结合平面模型Ax+By+Cz+D=0对隧道底部点云进行分割,分割情况如下：

(1)设置迭代次数n为500,λ为0.01 m,如图9(a)所示为提取到的最优平面模型内的点云,可以观察到由于底面点云并非在同一平面内,而是有一定厚度的点云面片,因此当λ较小时RANSAC算法提取到的最优平面点云只是底面。

(2)设置迭代次数n为500,λ为0.2 m;如图9(b)所示为提取到的最优平面模型内的点云,可以观察到当λ较大时RANSAC算法提取到的最优平面点云为部分切片,而不是底部平面点云。

(3)设置迭代次数n为500,λ为0.06 m,如图9(c)所示为提取到的最优平面模型内的点云,可以观察到RANSAC算法提取到的最优平面点云为底面点云。

(a) λ为0.01 m (b) λ为0.2 m

(c) λ为0.6 m图9 横断面分割

从图9中可以看到直接使用平面模型进行选取最优参数时,计算机经常会选择出符合平面模型参数的非底面点云,这是因为虽然该部分并非平面或者并非全部底面,但在数学模型内却包含最多点云。此外测量作业中还会出现点云缺失、漏测、点云密度不均、点云解算软件的内插操作等各种情况,往往造成平面模型的不确定性,进而使得选取参数时产生不确定性。因此就需要工作人员不断调节误差阈值λ,以使RANSAC模型提取出的是平面点云;然而这就使得工作效率较低,且可能出现同样阈值λ在部分切片分割出了平面点云,部分切片分割出了非平面点云,进而需要对不同切片使用不同阈值λ,这就进一步增加了操作的复杂性。

针对该种情况,本文加入法向量τ(υ,ω,ξ)约束,利用法向量自动选取出符合底面特征的最优平面模型。

由图7中的中线可求得隧道坡度在15°上下波动,因此设置法向量τ(υ,ω,ξ)为(0,-0.26,1),将该法向量作为平面模型内点云的约束,约束角θ为15°,设置迭代次数n为500;由于底面矩形高h为0.355 m,部分高度略有偏差,因此λ应略微大于h;且由于有法向量作约束,因此λ可取较大值,本文设置为0.36 m。将切片内的点云向横断面方程进行投影从而获取横断面轮廓线,由图10中可观察到隧道切片得到了完整分割。

图10 横断面分割

3.2.2 横断面拟合及滤波降噪

混凝土厚度检测、隧道表面起伏差检测、隧道表面的变形监测都需要横断面作为重要参数。因此对横断面进行提取及拟合是三维激光技术中的重要工作。

(1)将隧道切片进行旋转,从原始坐标系中旋转至拟合坐标系,如图11所示,图中旋转后的切片点云平行于XOY平面,从而实现三维数据向二维数据的转化,为横断面拟合做准备。

图11 横断面切片旋转

(2)直接使用最小二乘结合椭圆模型拟合,如图12所示。从图中可以观察到拟合横断面形状与隧道原始形状差距较大。

图12 直接拟合

(3)使用剔除掉底部点云后的横断面进行拟合,如图13所示。从图中可观察到拟合横断面与原始横断面形状接近,更能反映隧道原始横断面的真实情况。

图13 横断面切割底面后拟合

(4)横断面滤波。对横断面进行最小二乘拟合后即可根据横断面参数对横断面轮廓点云进行降噪,本文取局部隧道共334 000个点进行滤波分析。如图14所示为降噪前后的误差分布图,由图可观察到滤波前误差分布在-0.3～0.15 m;滤波后误差分布在-0.1～0.1 m,滤波前后误差分布改变明显,非点得到明显剔除。

(a)滤波前

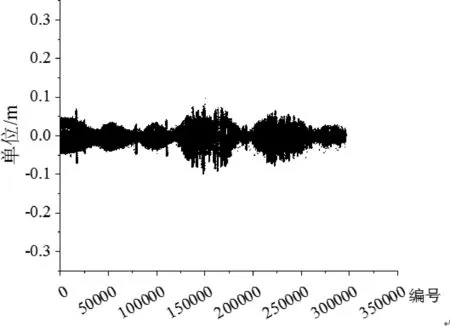
(b)滤波后图14 滤波前后误差分布图

对滤波前后的噪点进行统计分析,从表2中可观察到剔除噪点37 598个;平均值从-0.009 m降低至0 m;均方差从0.041 m降低至0.019 m,滤波前后误差明显降低。综上所述本文降噪效果较好,降噪方法较优。

表2 去噪前后误差分析

4 结束语

本文针对隧道底部为矩形的隧道横断面分割、拟合及滤波提出了一种利用隧道腰部边界特征提取隧道腰部中线,接着依据隧道腰部中线提取隧道横断面,最后剔除出隧道底部点云并拟合横断面。得出以下结论：

(1)针对半圆形隧道上下不对称、中线难以提取的特点,本文依据边界特征提取隧道腰部边界,进而提取腰部中线,并使用设计中桩进行检验;实验表明本文提取中线与设计中线桩点ΔX、ΔY均在11 mm以内,ΔZ在15 mm以内,提取精度较高,效果良好。

(2)针对半圆形隧道横断面提取问题,依据底面坡度数据计算法向量,在平面检核中作为约束条件进行参数求取;接着根据隧道下部矩形设计高度进行分割。相比于直接使用RANSAC进行平面检核,该方法针对性更强,分割效果更好。

(3)使用剔除掉底部点云的隧道横断面进行拟合,相比于直接使用最小二乘法横断面拟合该方法形状较为符合横断面形状。根据最小二乘原理对横断面点云进行滤波并以局部隧道进行实验验证,滤波前误差分布在-0.3～0.15 m,滤波后误差分布在-0.1～0.1 m;此外滤波前后均方根误差分别为0.041 m和0.019 m,综上所述本文方法拟合精度较高。