利用海潮模型研究D-InSAR中的海潮负荷效应

欧阳亿王琪洁，2魏国光

1中南大学地球科学与信息物理学院，湖南 长沙，410083

2中南大学有色金属成矿预测与地质环境监测教育部重点实验室，湖南长沙，410083

日月对地球产生的引潮力作用会使地球发生潮汐现象，其中海洋潮汐会引起海水质量重新分布，进而使固体地球产生弹性形变，即海潮负荷（ocean tide loading，OTL）。在沿海地区，海潮负荷引起的形变可达数厘米。因此，在沿海地区的精密空间地表测量中，必须顾及海潮负荷的影响。当前，有关InSAR（interferometric synthetic aperture radar）研究微小形变方面仅有少量学者在研究冰川运动时考虑过海潮负荷［1］。所以，研究沿海地区InSAR中的海潮负荷效应，对提高InSAR精度和可靠性方面具有非常重要的实际意义［2-5］。

目前，研究海潮负荷的手段包括海潮模型、GPS、VLBI等。与VLBI、SLR技术相比，GPS、海潮模型具有低成本，高精度的优势。因此，本文以美国加州沿海区域为例，首先评估FES2004以及HAMTIDE11A两个全球海潮模型和osu.usawest.2010区域海潮模型的精度，根据评估结果构建合适的组合模型，然后使用不同海潮模型对比分析D-InSAR（differential InSAR）中的海潮负荷效应。同时，与GPS PPP（precise point positioning）静态定位结果对比分析。

1 模型精度评定及海潮负荷计算

1.1 模型精度评定

本文基于南加州8个验潮站测高数据，采用公式（1）计算海潮负荷中影响较大的8个分潮（M2、N2、S2、K2、K1、P1、O1、Q1）的 中 误 差（root mean square，RMS），然后根据8个分潮的RMS值，利用式（2）计算总体综合预报误差（root sum squares，RSS）来评定海潮模型精度［6］，公式为：

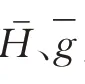
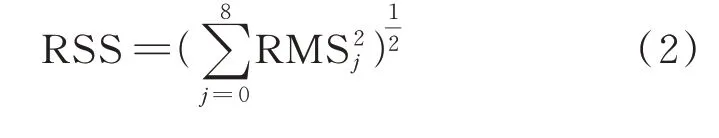
1.2 海潮负荷位移计算

全球海潮模型主要利用潮高和格林函数褶积积分［7］计算海潮负荷位移：

然而，近海区域海底地形和海岸线复杂，全球海潮模型计算近海区域的海潮负荷位移精度不高。因此，本文利用区域海潮模型来精化全球海潮模型，其精化公式为：

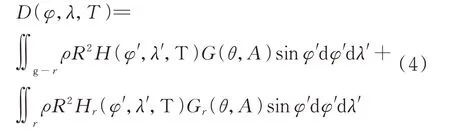
式中，D(φ，λ，T)是T时刻测站的海潮负荷位移；ρ是海水密度；φ是计算点的纬度；λ是计算点经度；φ′和λ′分别为负荷点的纬度和经度；R为地球半径；H(φ′，λ′，t)和Hr(φ′，λ′，t)分别是全球海域g和近海海域r中负荷点的瞬时潮高；G(θ，A)和Gr(θ，A)为Green函数；θ和A分别是计算点到负荷点的球面距离和方位角，且A位于（0，2π）区间，θ可以通过式（5）获得：

2 海潮模型精化

2.1 研究区域与数据

本文选取美国加州地区8个验潮站对海潮模型进行精度评估。同时，也选取南加州38个GNSS测站计算海潮负荷位移。验潮站和GNSS测站的位置如图1所示。图1（a）选取验潮站需要满足3个条件：①验潮站位于海潮模型计算范围内；②验潮站均匀分布在美国加州沿海地区；③验潮站近两年数据资料完整。基于此3个条件，从图1（a）的15个验潮站中选取了8个验潮站。

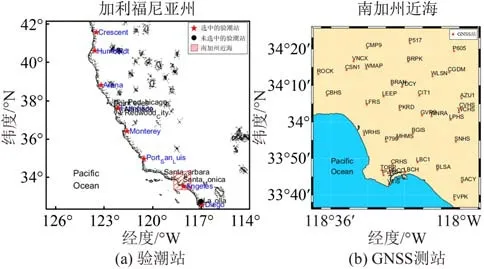
图1 站点分布图Fig.1 Map of Station

2.2 海潮模型选取和计算

本文选取两个精度较高且常用的全球海潮模型FES2004模型以及HAMTIDE11A模型和一个覆盖美国西海岸的区域海潮模型osu.usawest.2010模型［8，9］。选取组合海潮模型计算海潮负荷位移的具体步骤分为两步：

1）利用加州沿海8个验潮站资料对海潮模型进行精度评定，并选取合适的海潮模型组合；

2）采用不同海潮模型计算D-InSAR中的海潮负荷位移。

表1与表2分别是根据式（1）与式（2）计算的8个分潮的分潮综合预报中误差RMS和分潮总体综合预报误差RSS。

表1 不同海潮模型的RMS/cmTab.1 RMS of Different Ocean Tide Model/cm

表2 不同海潮模型的RSS/cmTab.2 RSS of Different Ocean Tide Models/cm

在表1所示的8个分潮中，M2分潮的RMS值超过20 cm，而Q1分潮的RMS值小于1 cm。这说明在加州沿海区域中，海潮模型计算M2分潮的精度较低，计算Q1分潮的精度较高。在3个海潮模型RSS值 中，HAMTIDE11A模 型 最 大；FES2004模 型 次之；osu.usawest2010最小。可以得到：在美国加州沿海区域中，区域海潮模型osu.usawest.2010有精度优势，且在两个全球海潮模型中，FES2004模型的精度比HAMTIDE11A模型高。区域海潮模型osu.usawest.2010相较于两个全球海潮模型具有精度优势的原因是其考虑南加州近海域的影响时，具有更高的分辨率。因此，可以依据式（4）和式（5）将区域海潮模型osu.usawest.2010精化全球海潮模型FES2004（简称OF组合模型）。

基于OF组合模型，选取位于美国南加州沿海区域内的近海点P1（33.958°N，118.428°W）和远海点P2（34.341°N，117.937°W），并计算LOS方向上P1-P2的相对位移。如图2所示，其中图2（a）时段为2015-01-01T1：00：00—2015-03-24T8：00：00（时段1），图2（b）截取时段为图2（a）中2015-01-30T5：00：00—2015-02-03T9：00：00（时 段2）。在 图2（a）中，LOS向位移的周期与海潮负荷位移趋于一致；在图2（b）中，LOS向位移曲线与垂直向海潮负荷位移几乎重合，与东西（南北）向有差异。尤其在峰值时，LOS向位移达到25 mm，而东西（南北）向为10 mm。这说明LOS向位移主要受垂直向海潮负荷位移影响。

图2 两点的相对位移Fig.2 Relative Displacement of Two Points

3 海潮负荷位移结果对比与分析

3.1 不同海潮模型计算结果对比

本文以沿海CRHS站与LBCH站为例，对比OF组合模型与全球海潮模型FES2004计算的垂直向海潮负荷位移。

如图3所示，图3（a）为2015-01-01T1：00：00—2015-03-24T8：00：00时段（时段1），图（b）为图（a）时段的0～200 h时间序列图。从3（a）、3（b）两图，OF组合模型计算的位移曲线的相位与FES2004模型一致，而OF组合模型计算的振幅要低于全球海潮模型。说明OF组合模型计算海潮负荷位移的精度高于全球海潮模型FES2004。这是因为在计算南加州的海潮负荷位移时，OF组合模型不仅采用全球海潮模型FES2004的分辨率考虑了全球海域的影响，还基于区域海潮模型osu.usawest.2010的分辨率考虑了南加州近海域的影响。因此，OF组合模型比全球海潮模型FES2004更有优势。

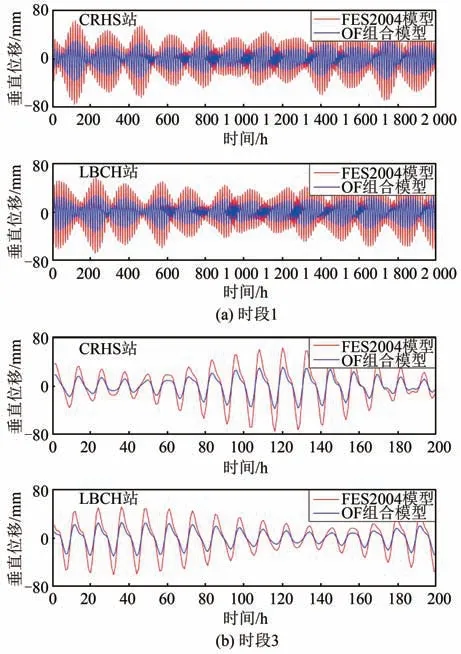
图3 组合模型和全球模型对比Fig.3 Comparison of Combined Models and Global Models

将不同海潮模型计算的海潮负荷位移转换至LOS方向，并将时间点为2015-01-01T20：00：00和2015-03-01T20：00：00的两幅图像进行差分，然后对不同海潮模型结果进行分析。如图4所示，FES2004模型计算的LOS向位移值的趋势与OF模型一致，但数值高于OF模型，且FES2004模型计算值近乎是OF模型的两倍。其主要原因是全球模型计算南加州海潮负荷位移的精度要低于组合模型。同时，结合图1可以发现在美国南加州中LOS向位移量越靠近内陆越小。这是因为从近海岸到内陆，海潮负荷影响逐渐减小。

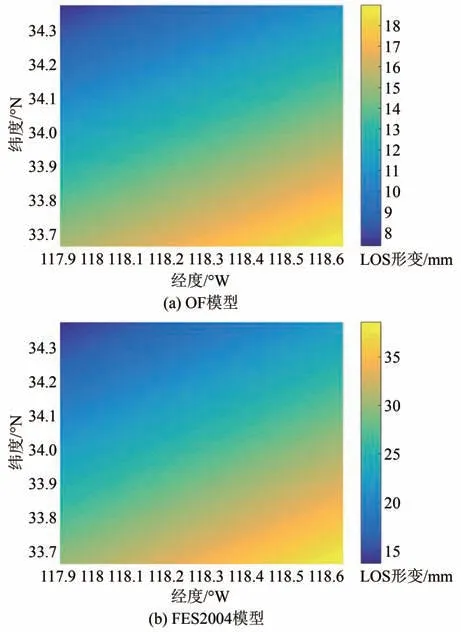
图4 不同海潮模型计算的LOS向位移Fig.4 LOS Direction Displacement Values Calculated by Different Ocean Tide Models

3.2 海潮模型计算结果与GPS观测值对比

本 文 利 用GPS PPP方 法［10-11］获 取 海 潮 负 荷 位移，转换为LOS向位移，并将结果与OF组合模型对比。考虑到离太平洋海域近的测站影响更大，因此，从38个测站中选取离海更近的两个测站：CRHS站和WRHS站，并将其2 h时长的GPS PPP计算的海潮负荷位移与OF组合模型计算的垂直向海潮负荷位移对比，时段为2015-02-20T1：00：00-2015-03-12T20：00：00约500 h。其结果证明：在CRHS站以及WRHS站中，GPS PPP反演值与OF组合模型计算的海潮负荷位移趋势一致。垂直位移对比如图5所示。

图5 GPS观测值与海潮模型计算海潮负荷位移对比Fig.5 Comparison of GPS Observations and Ocean Tide Model Calculations

接着，将GPS PPP计算的海潮负荷位移转换为LOS向位移，并与OF组合模型计算结果对比，以此来评估海潮模型计算LOS向位移的有效性。海潮负荷效应具有近双线性分布的空间特征［12-13］，可拟合成平面，因此可以将南加州沿海区域的38个GNSS站计算的LOS向位移模拟为线性面模型。利用OF组 合 模 型 计 算2015-01-01T20：00：00-2015-03-01T20：00：00（时段3）的38个GNSS站的LOS向位移，然后将其差分并模拟为线性面模型，如图6所示。

基于38个测站资料，将2015-01-01T20：00：00-2015-03-01T20：00：00的GPS PPP结 果 转 换 为LOS向位移，然后在南加州研究区域里将其差分并模拟为线性面模型，如图7所示。

本文又选取了另一组数据进行实验，时段为2015-01-04T1：00：00-2015-02-11T1：00：00（时段4）。OF组合模型计算这一时段内38个南加州沿海区域的LOS向位移，然后将其差分并模拟为线性面模型，如图8所示。

将2015-01-04T1：00：00--2015-02-11T1：00：00的GPS PPP结果转换的LOS向位移差分并拟合成线性面模型，如图9所示。

图6和图7表明，在趋势上，GPS PPP转换结果拟合得到的线性面与海潮模型拟合的线性面从左上向右下沿对角线方向增加；图8和图9表明：在趋势上，GPS PPP转换结果拟合得到的线性面与海潮模型拟合的线性面从左下向右上沿对角线方向增加；这两组不同时段的差分图像结果表明：在趋势上，两种方法拟合的线性面一致。

图6 OF组合海潮模型计算的相对海潮负荷位移转换为LOS方向（时段3）Fig.6 Relative Ocean Tide Load Displacement Calculated by the of Combined Ocean Tide Model Is Converted to the LOS Direction（Time 3）

图7 GPS PPP解算的相对海潮负荷位移转换为LOS方向（时段3）Fig.7 Relative Ocean Tide Load Displacement of the GPS PPP Solution is Converted to the LOS Direction（Time 3）

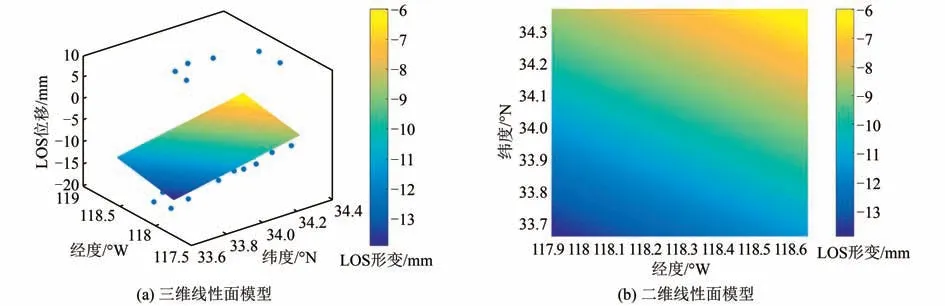
图8 OF组合海潮模型计算的相对海潮负荷位移转换为LOS方向（时段4）Fig.9 Relative Ocean Tide Load Displacement Calculated by the OF Combined Ocean Tide Model is Converted to the LOS Direction（Time 4）

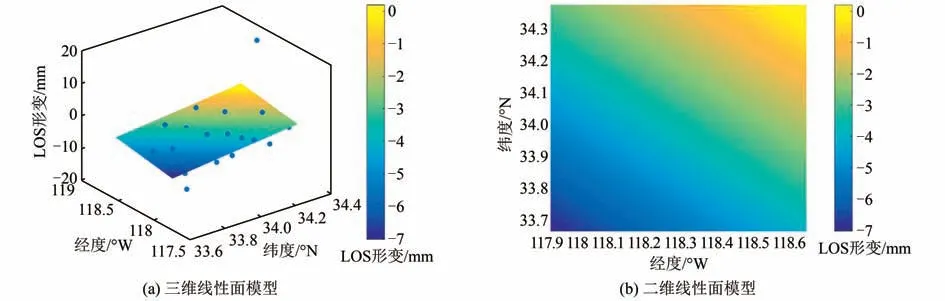
图9 GPS PPP解算的相对海潮负荷位移转换Fig.9 Relative Ocean Tide Load Displacement of the PPP Solution is Converted to the LOS Direction（Time 4）

最后，为了对比OF组合模型与GPS PPP结果转换的LOS方向位移值。随机选取100个坐标序列，将基于这两种技术计算的LOS方向位移值作差对比分析可知：OF组合模型与GPS PPP计算的LOS向位移值相差3～4 mm；而OF组合模型与GPS PPP结果转换的LOS向位移值相差6 mm。这说明：在数值上，这两种技术计算的L O S向位移值差异较小。因此，O F组合模型以及G P S P P P结果转换的L O S向位移在趋势上是大致相等的。这可以证明O F组合模型研究D-I n S A R中的海潮负荷位移是有效的；同时，不同海潮模型计算的DI n S A R中的海潮负荷位移均达到了厘米级。因此，在近海地区的D-I n S A R测量中，有必要考虑海潮负荷位移的影响。

4 结束语

通过评估两个全球海潮模型（FES2004以及HAMTIDE11A）和一个区域海潮模型（osu.usawest.2010）在美国加州沿海区域的精度，可以发现区域海潮模型osu.usawest.2010的精度高于两个全球海潮模型，同时在两个全球海潮模型的精度对比中，FES2004模型精度较高。因此，采用osu.usawest.2010模 型 精 化FES2004模 型，即OF组 合模型计算D-InSAR的海潮负荷位移，并将结果与全球海潮模型FES2004以及GPS PPP定位结果的计算值进行比较，同时，利用100个坐标序列，分别将两个时段中OF组合模型和GPS PPP定位结果计算的LOS方向位移值作差对比，可以发现：两个时段的OF组合模型计算的LOS向位移值与GPS PPP计算值趋势一致，且在数值上最大相差6 mm。所以，OF组合模型计算的D-InSAR中的海潮负荷位移有效；相较于FES2004模型，采用OF组合模型研究D-InSAR的海潮负荷位移更具有优势；OF组合模型、全球海潮模型FES2004以及GPS PPP计算的LOS向位移都达到了厘米级。沿海区域的海潮负荷影响比内陆的海潮负荷影响大一个量级。所以，在沿海区域中利用D-InSAR测量微小形变时，须考虑海潮负荷引起的相对形变影响。