利用随机先验信息克服秩亏问题的方差分量估计

王 慧程 涵管守奎

1苏州挚途科技有限公司，江苏苏州，215000

秩亏往往意味着线性高斯-马尔可夫模型中缺少平差必要的信息，而先验信息可以解决这些信息缺失导致的秩亏问题，提供线性模型平差的基准。秩亏自由网平差［1］在大地测量中应用广泛，尤其在水准网、GPS基线测量以及大地坐标系框架体系建设［2］等存在缺少基准或起算数据时。利用先验信息解决秩亏问题也十分常见，但Meissl［3，4］以及Neimeier［5］提出利用新增的基准确定点存在不确定性，所以应将先验信息表示为带随机性质的先验信息。添加的先验信息作为一种约束需要满足正交方程有解并且不改变残差的值都可以认为是合理的［6，7］。利用先验信息使正交方程有解时应该将模型表示为混合模型［8］，或者扩展的高斯-马尔可夫模型［9］，这种混合模型的最小二乘估计通常称作最小二乘配置［10，11］，并在确定重力场的研究中广泛使用。

先验随机信息的可信度是解决秩亏平差时一个重要的问题，Schaffrin［12］提出一种稳健配置方法用于观测值信息和随机先验信息更合理的使用。

综上所述，利用随机先验信息克服秩亏问题的方差分量估计在秩亏网平差中的研究十分重要。本文利用最优不变二次无偏估计原理［13-16］，推导带有先验信息的高斯-马尔可夫模型的方差分量估计公式，从而做到对观测信息和随机先验信息进行合理配权，以提高秩亏网中基准的可靠程度。

1 最优不变二次无偏估计方差分量

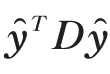
1）无偏性：

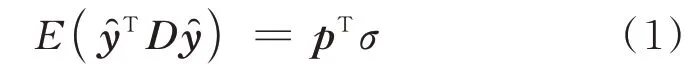
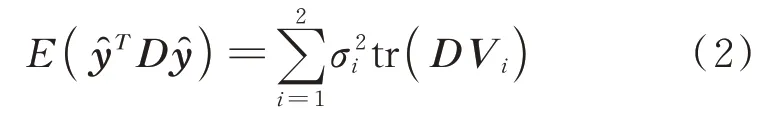
2）不变性：

3）最小方差：

将不变性式（3）带入式（5）得到：

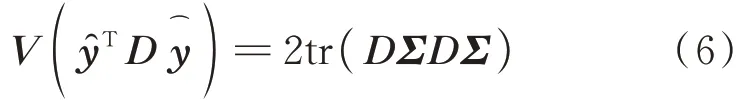
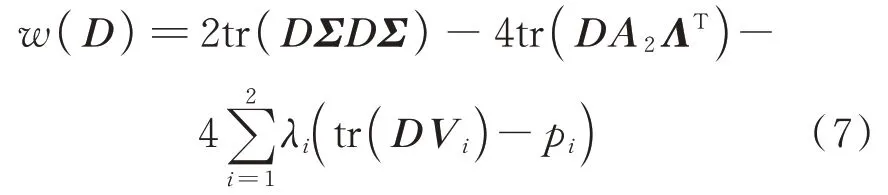
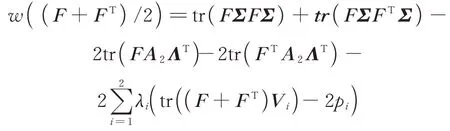
由∂tr(ABATC)/∂A=(BATC)T+CAB以 及∂w((F+FT)/2)/∂F=0，得到：

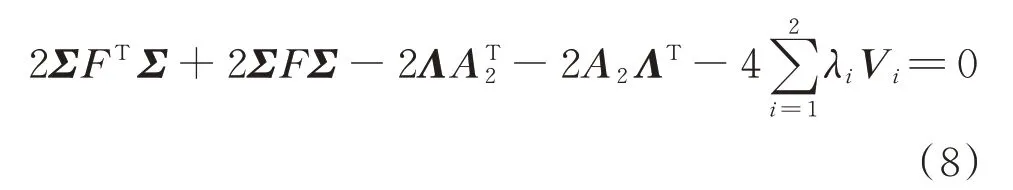
将D=(F+FT)/2带入式（8）中得到：

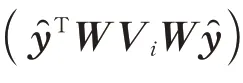
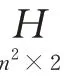
则

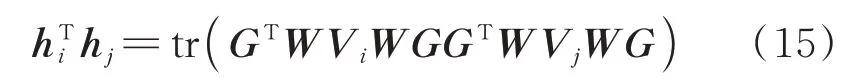
当S可 逆 时，则pT=[1，0]T∈R(S)且pT=[0，1]T∈R(S)，由式（13）可知方差分量的估值唯一确定为：

当S奇异时，则pT=[1，0]T∈R(S)或者pT=[0，1]T∈R(S)，由式（13）可知方差分量的估值唯一确定为：

当S可 逆 时，则pT=[1，0]T∈R(S)且pT=[0，1]T∈R(S)，由式（17）可知方差分量的方差估值唯一确定为：

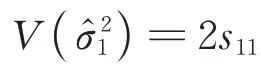
2 实例验证

表1 高差观测值表Table 1 High Difference Observation Value Table

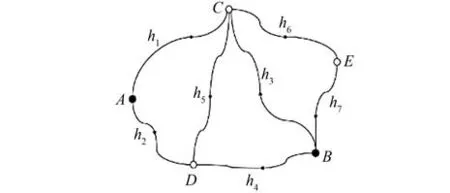
图1 高程水准网示意图Fig.1 Elevation Level Network Diagram

表2 误差估计值Table 2 Residual Estimate

计算中发现自第二次迭代后均收敛于1，于是在第二次计算完成后结束迭代计算。如表3、表4所示，得到最终估计的方差分量为5.452 3×10-6和3.949 5×10-7，两部分方差分量的比值为：0.072 4。相比于最小二乘估计单位权方差，方差分量估计更加准确的描述了带有先验信息的高斯-马尔可夫的随机模型，这也使得先验信息中的绝对基准更加合理可靠地应用在秩亏平差中。

表3 迭代计算结果Table 3 Iteration Calculation Results

表4 方差分量方差结果Table 4 The Variance of Variance Components Result

3 结束语

新增的先验信息常用作确定基准，但新增的先验信息带有随机性质，这意味着先验信息的可靠程度无法衡量。先验信息在平差模型中的不确定性需要寻求一种合理可靠的方法来度量先验信息和观测值，对两部分信息进行合理地分配权重，需要得到平差模型中准确的验后随机模型。本文利用最优不变二次无偏估计先验信息和观测值两部分的方差分量以及方差分量方差，得到验后随机模型，准确地描述两部分的权重。然后可以通过合理配权，从而进一步提高先验信息在解决秩亏网平差时的可靠性。