力反馈式电液伺服阀衔铁组件力学模型*
訚耀保,何承鹏,张鑫彬,王晓露,傅俊勇,原佳阳
(1.同济大学 机械与能源工程学院·上海·201804;2.上海航天控制技术研究所·上海·201109)
0 引 言
电液伺服阀是电液伺服系统的关键核心元件,其采用微弱电控信号控制大功率液压信号输出,已应用于航空航天、船舶、冶金等领域的重大工程装备。力反馈式电液伺服阀存在于电-磁-力-位移等多物理场信息转换过程。其中,电-磁-力的转换功能由电-机械转换器完成。力矩马达是最常见的电-机械转换器。文献[6]发现,当力矩马达气隙左右对称或上下对称时,气隙误差仅影响伺服阀增益,而气隙不对称时,会引起伺服阀零偏。文献[7]通过优化磁极阵列,提高了力矩马达输出力矩。
电液伺服阀作为高端液压元件,是我国重大装备用核心基础零部件(元器件)。衔铁组件连接着力矩马达和液压放大器,通过结构的柔性变形实现伺服阀电-磁-力-位移信息传递与转换的重要功能。工程实践中,衔铁组件零部件刚度被用来表征伺服阀力-位移信息转换的定量关系。刚度过低时,伺服阀运动部件易失稳;高刚度部件需要大电流驱动,会降低伺服阀功率密度比。零组件刚度还是伺服阀精密零件加工一致性的重要表征量。刚度超差是引起弹性精密件加工不合格的主要原因,制约着伺服阀生产。因此,精确预估衔铁组件结构刚度,对于伺服阀设计和生产具有重要实践意义。目前,常见的刚度确定方法有实验法、有限元法和解析模型法。国内学者陆续提出了手工吊码法、光学/电容/电感非接触式测位移法等精密零件刚度测量方法,不断提高测量精度和效率,用于精密零件检测环节。有限元法预估刚度精度高,但不能给出材料性能、几何尺寸与刚度间的解析关联式,结构设计实用性不强。衔铁组件零件形状复杂特殊,零组件刚度的精确计算存在一定困难,导致国内伺服阀弹性元件设计、材料选择和公差分配多依赖生产经验,缺乏理论指导。早期的两级伺服阀衔铁几何中心设有扭簧支撑,以该支撑为旋转中心,可用衔铁转动方程表征组件运动状态。为防止油液进入力矩马达气隙,研究人员采用弹簧管替代衔铁扭簧,并提出了旋转中心位于弹簧管薄壁段轴心线中点的假设条件,但该假设条件忽略了剪力对变形的影响,组件运动状态预测精度较低。文献[12]基于欧拉梁理论提出了力矩马达弹性元件综合刚度模型,但未对反馈杆、挡板等变截面精密件刚度的精确计算问题进行深入研究。
本文研究了喷嘴挡板式力反馈电液伺服阀中具有电-磁-力-位移信息传递与转换功能的衔铁组件,计及零件变截面特征和剪力的影响,基于卡氏第二定理,推导了实际工作状态下衔铁组件载荷-位移函数关系式,并提出了各精密零件/组件的刚度计算式。通过某型弹簧管、反馈杆的刚度测量试验,验证了刚度计算式的准确性,为电液伺服阀电-机械驱动器、射流放大器一体化匹配设计提供了参考。
1 喷嘴挡板电液伺服阀衔铁组件结构
喷嘴挡板电液伺服阀典型结构如图1所示。该阀由力矩马达、喷嘴挡板阀和功率滑阀等组成。衔铁组件连接力矩马达、挡板和功率滑阀,包括衔铁、弹簧管、挡板和反馈杆等零件。力矩马达通电后,衔铁产生电磁力矩。假定线圈输入正方向电流时,衔铁组件的力矩为逆时针方向,该力矩带动喷嘴挡板逆时针偏转,挡板与喷嘴间环形节流面积发生改变,导致滑阀阀芯左、右两侧容腔产生压差,推动滑阀向左移动。滑阀左移后,反馈杆末端随之向左移动,产生向右的反馈力并作用在反馈杆末端。当衔铁组件恢复力平衡后,滑阀稳定于某一位置,维持节流面积不变,输出与电流成比例的流量。可见,衔铁组件在电液伺服阀工作中起着力反馈和传递、位移输出的重要作用。
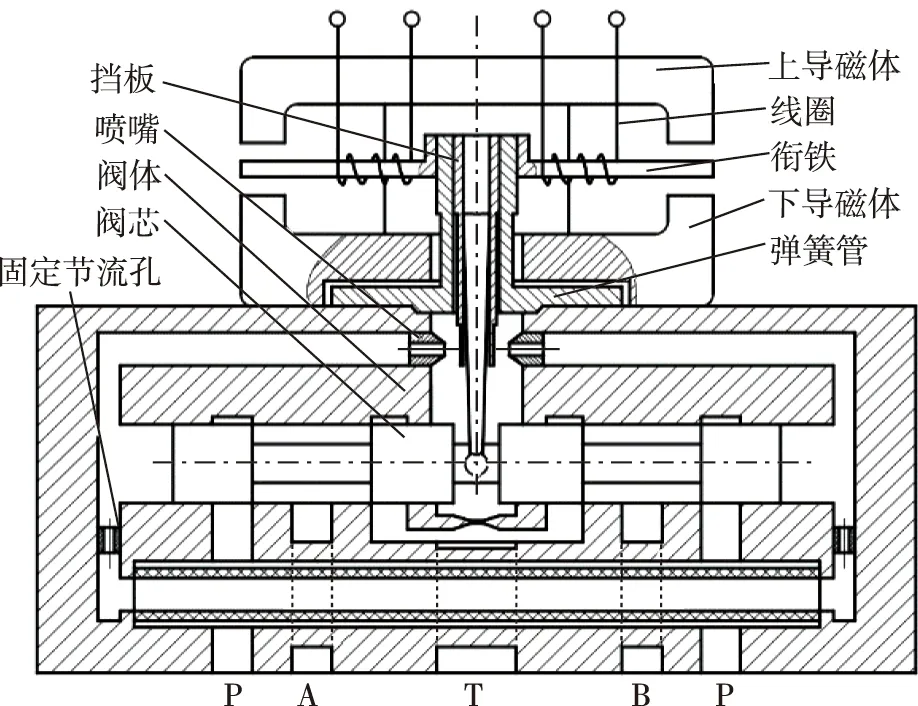
图1 双喷嘴挡板伺服阀结构示意图Fig.1 Components of double nozzle-flapper servo valve
常见的衔铁组件结构有两种:挡板和反馈杆分为两件的分离式结构、挡板和反馈杆为一体的整体式结构。图2所示为挡板反馈杆分离式衔铁组件结构。衔铁组件各部件采用过盈配合,如反馈杆大端外径与挡板内孔、挡板大端外径与弹簧管内孔、弹簧管头部外径与衔铁内孔等。反馈杆末端焊接一个小球,小球嵌入滑阀阀芯中部的凹槽。分离式结构中,挡板和反馈杆是2个独立的零件,常规分析中将这2个独立零件简化成一体,与实际结构受力变形存在差异,故本文着重研究分离式衔铁组件的力-位移精确转换关系。
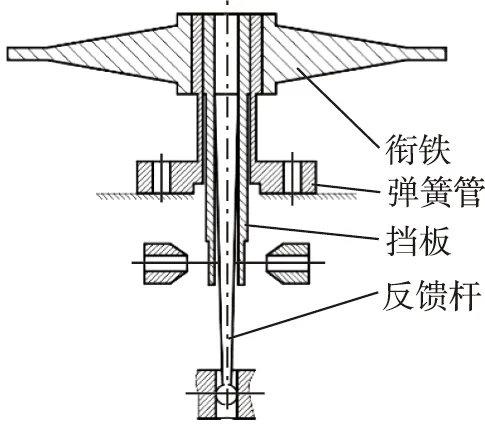
图2 挡板反馈杆分离式衔铁组件结构示意图Fig.2 Structure diagram of armature assembly with separated flapper and feedback rod
2 衔铁组件力学模型
2.1 服役时的衔铁组件载荷-位移关系模型
为便于分析,作以下假设:1)衔铁的横截面积较大,抗弯能力强,将衔铁作为刚体处理;2)不考虑组件内部过盈配合处的装配应力对组件变形的影响,不考虑焊接连接处残余应力;3)各零件材料均匀、连续且各向同性,其中弹簧管颈部壁厚约为60μm,抗弯能力最弱,故分析弹簧管变形时仅考虑颈部薄壁部分的变形;4)不计零件重力。
根据上述假设,将弹簧管等效成等截面梁,挡板和反馈杆等效为变截面梁,三者形成嵌套状结构,得到图3(a)所示弹性梁等价模型。工作状态下,衔铁组件承受的外载荷包括:力矩马达电磁力矩、喷嘴出流在挡板上的液动力、滑阀阀芯的反馈力。在3个载荷共同作用下,组件发生平面弯曲变形,直至外力(矩)和内力(矩)达到平衡,实现力(矩)-位移转换。本文考虑衔铁组件的复杂形状,着重分析衔铁转角、挡板位移、反馈杆球端位移与电磁力矩、射流液动力、阀芯处反作用力间的关系。简化后,变截面梁结构尺寸参数及截面形状如图3(b)所示。A~F为梁截面编号,挡板C-D段截面为中空鼓形,其余截面形状为圆形或环形。
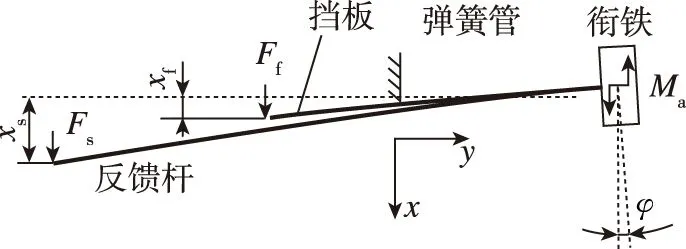
(a)弹性梁等价模型
将衔铁组件分为反馈杆、挡板和弹簧管三部分,与之相关的物理量符号的下标分别为r、f、s。对反馈杆,将杆件局部坐标系原点置于反馈小球中心,用截面法可以得到反馈杆内力和内弯矩分别为
()=,()=
(1)
式中,为局部坐标。反馈杆的应变能计算式为
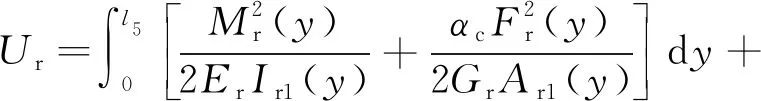

(2)

式中,、分别为反馈杆F-G段截面惯性矩和面积;、分别为反馈杆A-F段截面惯性矩和面积;为反馈杆材料弹性模量;为反馈杆材料剪切模量;为圆形截面剪切形状系数,取111;、、、、为衔铁组件尺寸链的参数。
同理,可得挡板应变能和弹簧管应变能分别为

(3)
=
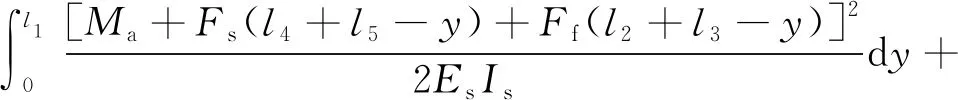

(4)
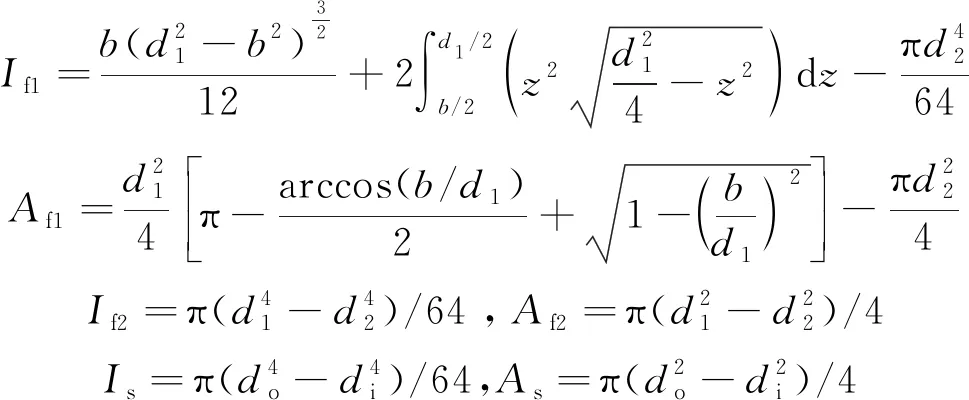
式中,为挡板材料弹性模量;、分别为挡板C-D段和A-C段截面惯性矩;、分别为挡板C-D段和A-C段截面惯性矩;为弹簧管弹性模量;为弹簧管薄壁部分截面惯性矩;为环形截面剪切形状系数,取2;为C-D段截面剪切形状系数,取1.6;、、为尺寸链参数,、分别为弹簧管薄壁部分外径和内径。
衔铁组件总应变能为
=++
(5)
卡氏第二定理阐释了应变能和载荷作用点位移间的关系,因其简便而且力学概念明确,在弹性元件静力学分析中得到了大量使用。弹性结构的应变能对作用在结构上的某个载荷的偏导数就等于该载荷作用点沿该载荷作用方向的位移

(6)
将式(1)~式(4)代入式(5),再代入式(6),采用分部积分法,可得衔铁组件的载荷-位移关系式为
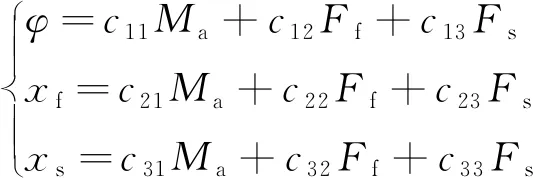
(7)
式中
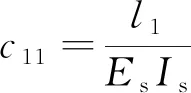
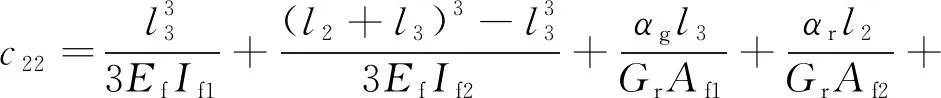

=

=,=

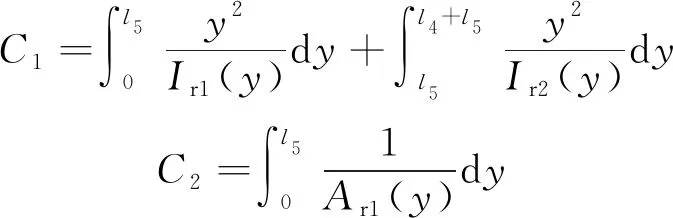
式中,(=1,2,3;=1,2,3)为由材料特性及结构决定的常数,具有柔度含义,表示单位第个载荷作用下第个载荷作用点位移,=1,2,3分别表示衔铁转角、挡板位移、反馈杆球端位移;=1,2,3分别表示电磁力矩、射流液动力、阀芯反作用力。由组成的矩阵为衔铁组件柔度矩阵。
由式(7)可知,载荷前的系数(=1,2,3;=1,2,3)由组件结构尺寸、材料力学性能、截面特征决定。已知衔铁组件结构参数时,无需假设旋转中心位置,可直接使用柔度矩阵模型进行伺服阀静态特性分析。
2.2 衔铁组件零部件刚度模型
各伺服阀生产厂家会逐个测量衔铁组件零件刚度,以便于调整加工余量,防止刚度超差,进而保证电液伺服阀批产性能稳定。刚度表示载荷与位移之比,是柔度的倒数。从2.1节中推导的柔度矩阵模型出发,可建立衔铁组件弹簧管、反馈杆、挡板等零件刚度和组件综合刚度,解析零组件刚度与材料性能、结构尺寸间的定量关系。
2.2.1 弹簧管刚度
根据外载荷施加方式,常用的弹簧管刚度有力矩-转角刚度和力-位移刚度。弹簧管力矩-转角刚度表示弹簧管头部力矩载荷与头部偏转的角度之比,与式(7)中的互为倒数。可得弹簧管刚度力矩-转角刚度计算式为
=1
(8)
因力矩加载比较困难,各厂家使用砝码重力或带力传感器的进给机构进行力加载。图4所示为弹簧管加载变形示意图。固定弹簧管底座,在弹簧管头部某点M处吊挂一质量为的砝码(相当于施加集中力,=)。或者通过直线进给机构,在M点施加力载荷,通过力传感器获取加载力。在砝码重力或进给机构作用下,弹簧管发生弯曲变形,变形后M点挠度为。则弹簧管力-位移刚度可表示为
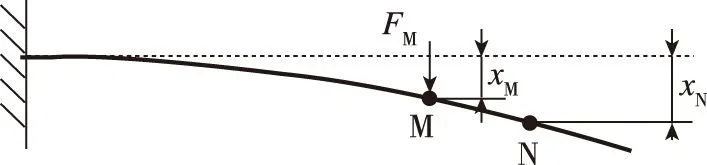
图4 弹簧管变形示意图Fig.4 Diagram of spring tube deformation
=
(9)
出于测量方便性和可重复性考虑,使用显微镜或工业相机获得N点处的位移,N点可能与M点重合,也可能位于弹簧管头部异于M点的另一点。该弹簧管刚度加载方式与其实际工作时受力不一致,而且测量的位移也不一定是加载点的位移,需要将N点的位移转换为M点的位移。沿用2.1节中的方法,可推导出、与间的函数关系为
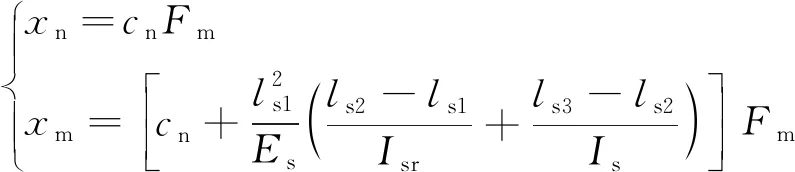
(10)
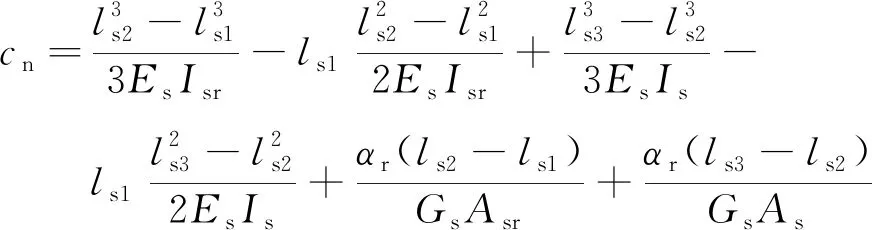
式中,为M、N点间距离;为N点到弹簧管头部下端面的距离;为N点到弹簧管法兰部上端面的距离;为弹簧管头部外径;、分别为弹簧管头部截面惯性矩和截面积,=π(-)64,=π(-)4。
由式(10)可进一步得到、间转换式
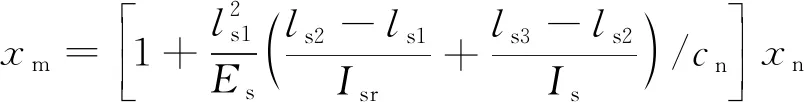
(11)
实际测量时,可先测量N点变形量,使用式(11)转换为M点处弹簧管变形量,再利用式(9)计算得到弹簧管力-位移刚度。
2.2.2 挡板刚度
挡板刚度定义为挡板射流冲击点处的垂直力与载荷施加点的弹性位移之比,计算式为

2.2.3 反馈杆刚度
杆端小球处的垂直力与载荷施加点的弹性位移之比即反馈杆刚度,计算式为
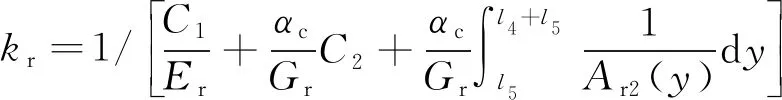
(12)
2.2.4 组件综合刚度
当衔铁组件装配完成后,在衔铁一侧施加垂直于表面的作用力,形成力矩载荷,该力矩与反馈小球位移之比即组件综合刚度,计算式为
=1
3 理论结果与实验结果的对比分析
3.1 弹簧管力-位移刚度测量实验装置及结果分析
为验证前述刚度计算方法的正确性,对某型号电液伺服阀弹簧管进行刚度测量。测量原理如图5所示。使用螺栓固定弹簧管,再打开透射光源。弹簧管遮挡部分光线,遮挡部分轮廓被电耦合器件(Charge Coupled Device,CCD)相机采集。先使用CCD相机拍摄弹簧管变形前的图像,再使用微进给机构对弹簧管头部中间位置进行力加载,并通过进给头上的力传感器获取加载力。当加载力为5.88N时,再次使用CCD相机拍摄变形后的图像。通过计算机对采集的图像进行处理,提取边界,经运算得到轮廓边界点的坐标值。根据坐标值可以得出弹簧管头部边界位置变化量,进一步得到弹簧管头部中间位置位移。重复上述步骤,对同一弹簧管重复测量三次位移。
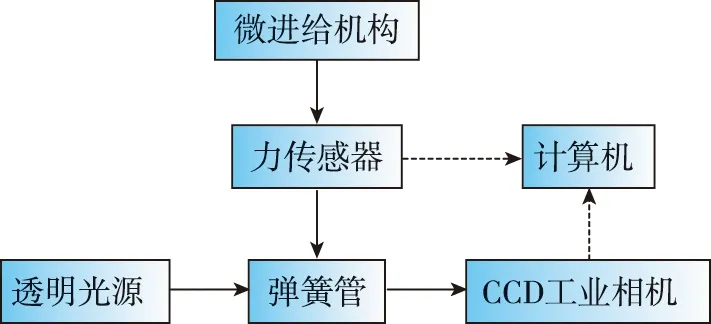
图5 弹簧管刚度测量原理Fig.5 Measurement principle of spring tube stiffness
图6所示为弹簧管刚度测量试验台。该试验台使用AVT Prosilca GT1920型彩色工业相机(分辨率为1936×1456,像元尺寸为4.54μm × 4.54μm)。在10万级净化车间中进行刚度测试,室内温度20℃,湿度控制在30%~45%。图7所示为测试对象某型电液伺服阀弹簧管实物图。对该弹簧管重复进行三次位移测量,三次位移测量结果分别为9.77μm、9.93μm和9.82μm。表1列出了测试对象的结构参数及材料力学性能。

图6 弹簧管刚度测量试验台Fig.6 Test bench of force-displacement stiffness of spring tube

(a)视角1
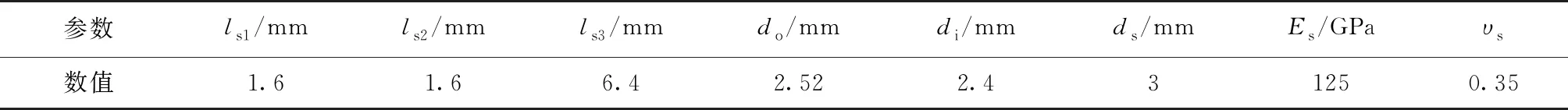
表1 测试对象某型弹簧管结构参数及材料力学性能Tab.1 Structural parameters and material properties of the tested spring tube
取三次测量结果的平均值作为载荷施加位置位移的最终测量值,再利用式(9)换算得到弹簧管的实测力-位移刚度,列于表2。将表1中的参数代入式(10),可计算出该弹簧管力-位移刚度理论值。弹簧管实测刚度和理论刚度相对误差为4.01%,二者较吻合。若不考虑剪力影响,则计算得到的弹簧管刚度值为0.778N/μm,与实测刚度相对误差为30.06%,可见剪力对弹簧管变形的影响不能忽略。

表2 弹簧管力-位移刚度实测值与理论值对比Tab.2 Comparison of the measured and theoretical force-displacement stiffness of the spring tube
3.2 反馈杆柔度测量结果和理论结果对比分析
YF-19-3型反馈杆尺寸参数为:=20mm、=0.286mm、=1.2mm、=0.56mm、=0.8mm。该型反馈杆使用弹性合金3J01(Ni36CrTiAl),该材料弹性模量和泊松比分别为195GPa、0.3。由式(12)计算得到该反馈杆刚度,取倒数后作为反馈杆柔度理论值,计算结果为304.81μm/N。该反馈杆柔度实测值为310.84μm/N。反馈杆柔度实测值与理论值的相对误差为1.94%。若不考虑剪力影响,则计算得到的反馈杆柔度值为304.24μm/N,与反馈杆实测刚度相对误差为2.12%。可见剪力对反馈杆变形的影响较小,主要原因在于反馈杆细长比大,与弯矩引起的挠度相比,剪力引起的变形量较小。
4 结 论
1)力反馈式电液伺服阀衔铁组件实现了电-磁-力-位移的信息传递与转换功能。提出了挡板反馈杆分离式衔铁组件的一种弹性梁等价模型,并基于卡氏第二定理建立了该结构静力学解析模型,推导了柔度矩阵表达式,提出了弹簧管、挡板、反馈杆等零件刚度和衔铁组件综合刚度计算方法,可为电液伺服阀动静态特性分析提供基础。
2)弹簧管实测刚度和反馈杆实测柔度与理论计算结果吻合,所提出的刚度计算模型较准确,可适用于复杂环境下服役的电液伺服阀衔铁组件精密零件的优化设计。
3)力-位移刚度测量过程中,横向加载力引起的剪力显著影响弹簧管变形,但对反馈杆变形的影响较小。考虑剪力对变形的影响可提高精密零部件刚度的计算精度。

