三灰度编码相位展开方法条纹投影轮廓术

张 昂，孙亚琴，高 楠，孟召宗，张宗华

（河北工业大学 机械工程学院，天津 300130）

1 引 言

条纹投影轮廓术［1］具有非接触、高精度等优点，被广泛应用在光学三维形貌测量中。相移轮廓术［3］和傅里叶变换轮廓术［4］是条纹投影轮廓术获取相位的两种主要方式。条纹投影轮廓术测量物体时，投影仪投射正弦相移条纹到被测物体上，通过相机采集的变形正弦条纹图像，利用变形正弦条纹图进行反正切计算的相位被包裹在[-π，π]，包裹相位中携带物体表面的深度信息，需要通过相位展开算法对包裹相位进行展开［5］。利用展开的相位与深度之间的关系，对物体的三维形貌进行重建。

现有的相位展开方法主要分为两类，空间相位展开法［5］和时间相位展开法［6］。空间相位展开法不适用于大梯度非连续表面，因此通过编码图像辅助的时间相位展开法更为常用，包括空间编码、相位编码、多频和格雷码方法。空间编码［8］值的获取需要该像素点以及邻域内的其他像素携带的颜色、强度等特征，抗干扰能力差、编码解码过程复杂。相位编码［9］使用阶梯相位来确定条纹级次，该方法受到环境光、物体表面的颜色纹理和非线性的影响，在条纹级次边缘处会出现相位误差，通常需要多幅相位编码图像来减少相位误差。多频方法［10］使用不同频率的正弦相移条纹图像来计算相位，最少需要双频（即6幅图像）来进行相位展开，同时双频相位展开方法易受到噪声的影响。格雷码方法［11］通过唯一的编码值来确定每个条纹周期的展开相位级次，如果投影的条纹图像包括f个周期，n灰度级格雷码则需要幅格雷码图像，其中表示向上取整。

多频方法［10］、傅里叶变换方法［12］以及格雷码［11］方法是目前相位展开的主要方法。Zheng等［11］将二进制格雷码改进到三进制格雷码，对于投影的条纹图像包括f个周期，仅需要投射幅格雷码图像。然而，格雷码方法通过投射时间序列编码图像来保证编码值的唯一性，对于条纹周期f≥16的条纹图像，仍需投射n＞3幅的格雷码图像。Qian［12］通过窗式傅里叶变换法从一幅条纹图像获取展开相位，但这种方法对非连续物体表面的测量结果并不理想。Zhang等［14］提出利用最佳三条纹选择法对物体进行相位展开，获得的展开相位是通过独立的像素点解算得到的，不受其他像素的影响，可实现对非连续物体的高精度测量。然而，在测量过程中需要投射和采集12幅条纹图像，测量时间较长。

为了实现快速三维形貌测量的同时保证测量精度，本文提出了一种利用空间邻域信息的三灰度编码相位展开方法。该方法利用空间邻域的编码值确定相位展开级次，在一个条纹周期内有较高的鲁棒性，无需复杂的解码过程，能够检测非连续表面。将三灰度编码相位展开方法与三步相移方法结合，对三步相移算法计算的包裹相位进行展开，只需投射和采集5幅条纹图像即可完成对物体三维形貌的恢复，提高了三维测量的重建效率。

2 基本原理

正弦相移与三灰度编码三维物体测量的整体框架如图1所示（彩图见期刊电子版）。其中，绿色部分描述了通过三幅正弦条纹图提取包裹相位；橙色部分描述了通过两幅三灰度编码图像获取相位级次；蓝色部分描述了通过获取的相位级次对提取的包裹相位进行展开，然后将对准误差去除后得到最终的展开相位；黄色部分描述了通过系统标定获得的标定系数结合最终的展开相位恢复物体的三维形貌。

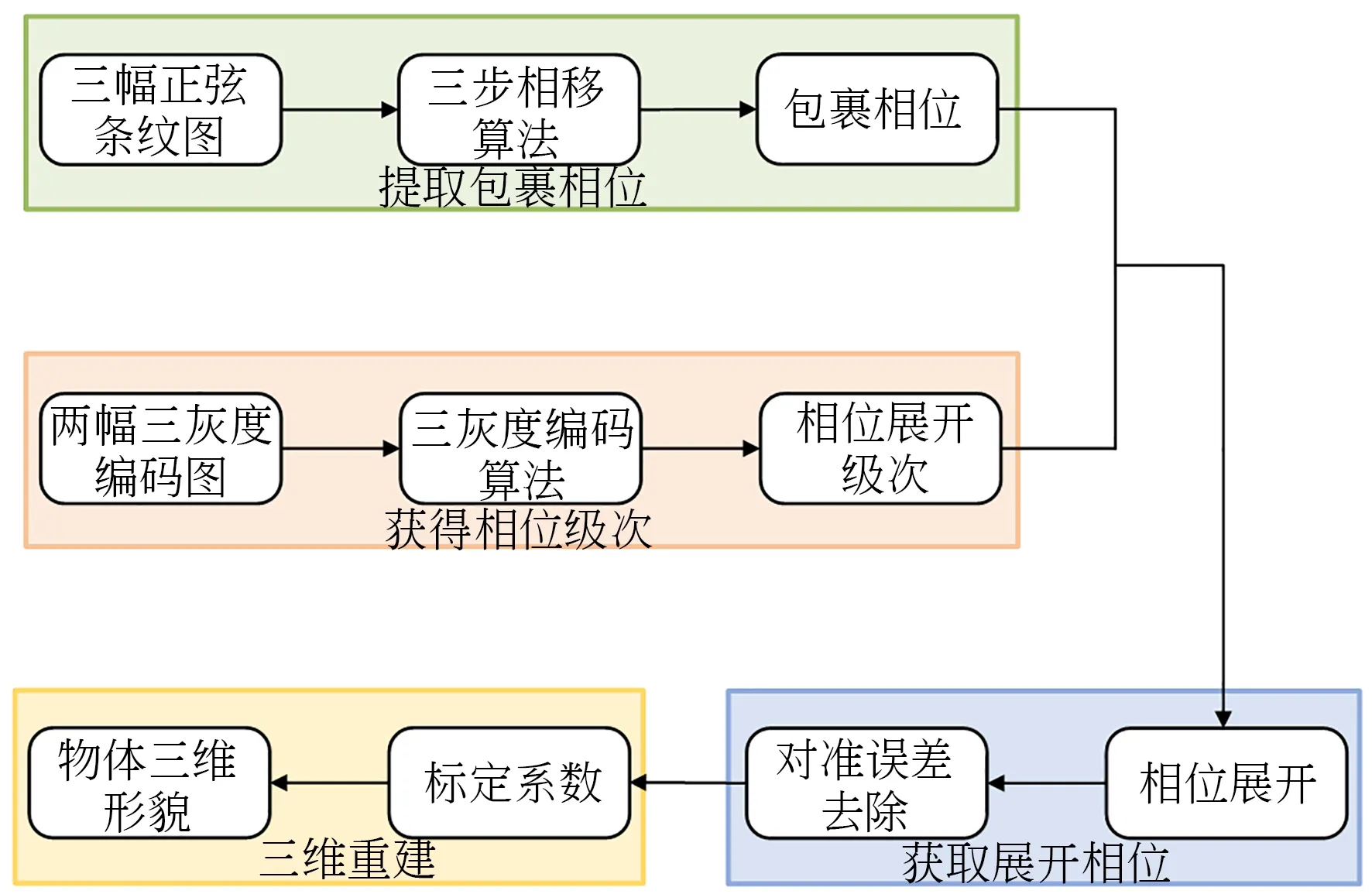
图1 正弦相移与三灰度编码三维测量的整体框架Fig.1 Framework of three-dimensional measurement of sinusoidal phase shift and ternary-gray encoded

2.1 正弦相移算法

相移测量方法具有高空间分辨率的优点，为了实现快速测量，通常使用三步正弦相移条纹图像来计算包裹相位，三步正弦相移图像可描述为：

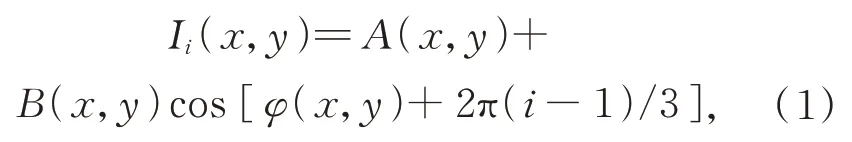
其中：i=1，2，3，φ(x，y)为包含被测物体深度信息的包裹相位信息，A(x，y)为条纹背景光强，B(x，y)为条纹调制度。由于环境光和物体表面属性的影响，A(x，y)和B(x，y)都是空间变化的。包裹相位可由三步相移算法计算得出：

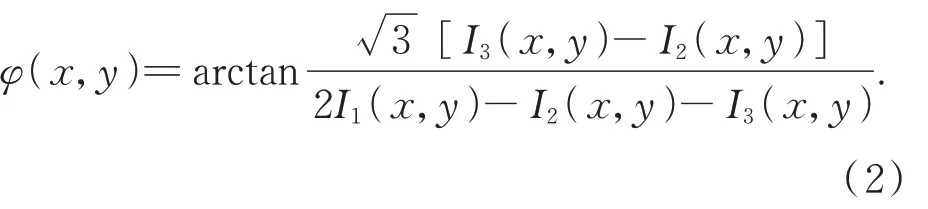
条纹背景光强为：

2.2 三灰度解码

三灰度编码图像如图2所示。其中，第1行为第一幅三灰度编码图像，第2行为第二幅三灰度编码图像，黑色代表灰度值为0对应三值化后的码值0，灰色代表灰度值为128对应三值化后的码值1，白色代表灰度值为255对应三值化后的码值2。三灰度编码以40个码值为例，编码方法并不唯一，一旦确定编码方法，码值顺序固定不变，可用于确定条纹级次。

图2 三灰度编码图像Fig.2 Ternary-gray encoded image

三灰度解码算法流程如图3所示。将相机采集的两幅三灰度编码图像经过空间灰度平均-灰度三值化-灰色伪码去除后得到编码值，然后利用编码值确定展开相位级次。

图3 三灰度解码算法流程Fig.3 Flowchart of ternary-gray decoded algorithm

2.2.1 空间灰度平均

由于投影仪投射条纹图案到物体上时光强并不是均匀分布的，相机采集到的三灰度编码图像的灰度并不是空间均匀的。采集到的一幅三灰度编码平板图像如图4（a）所示，从采集平板图像的中间行剖面图可以看出，相机采集的图像灰度值呈现左低右高的现象。这种空间灰度不均匀的现象会影响到灰度三值化，因此，需要通过式（4）来对采集的编码图像进行空间灰度平均，最终空间灰度平均处理后的编码图像以及中间行剖面图如图4（c）～4（d）所示。空间灰度平均后编码图像的光强空间分布更加均匀，具有更高的对比度，便于后续的灰度三值化处理。

其中：i=1，2，Ap(x，y)，Ac(x，y)分别为投射和采集正弦相移条纹图像的条纹背景光强，为相机采集的三灰度编码图像，为空间灰度平均处理后的三灰度编码图像。

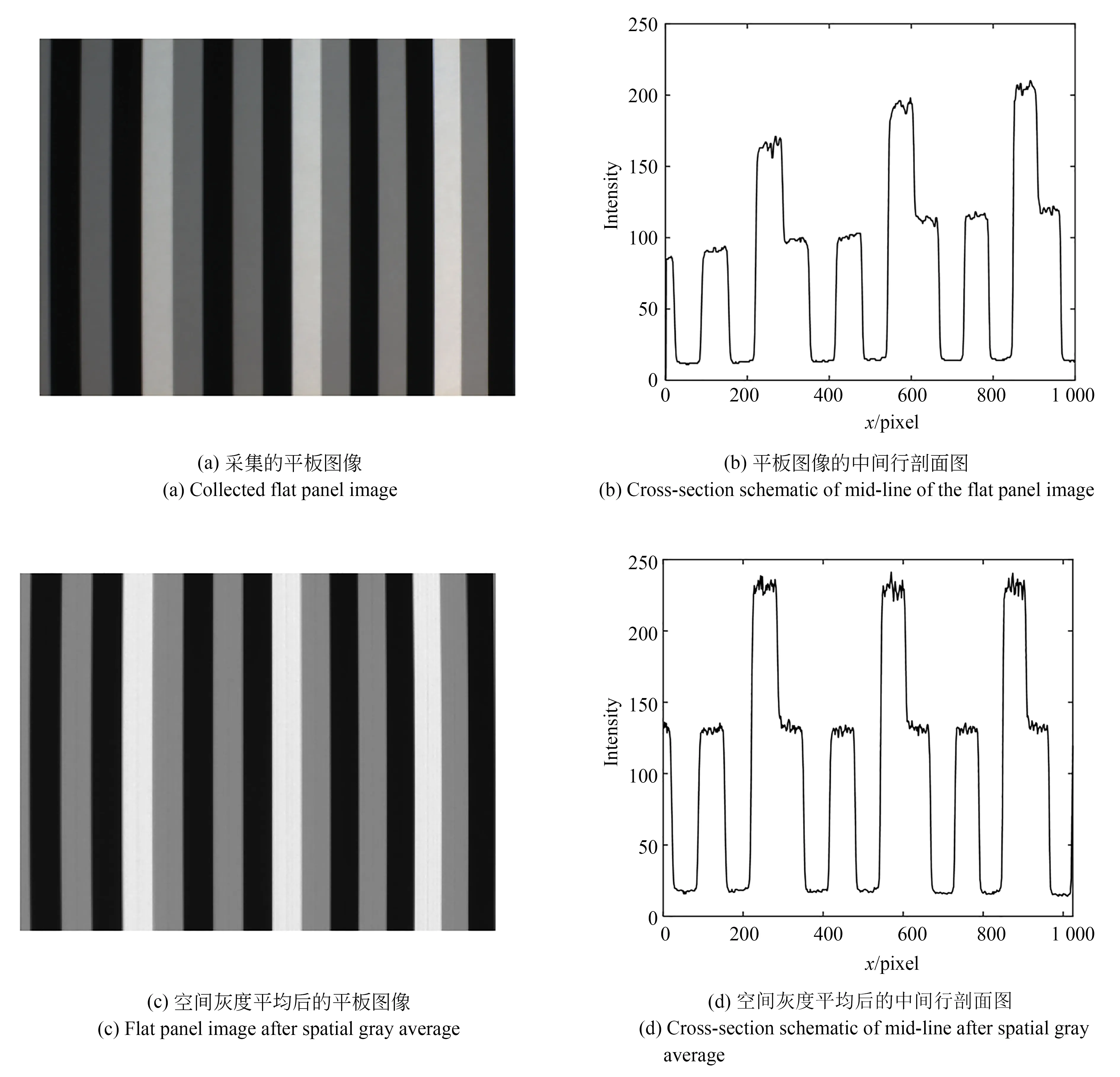
图4 三灰度编码图的空间灰度平均Fig.4 Spatial gray average of ternary-gray coded images

2.2.2 灰度三值化

2.2.3 灰色伪码去除

灰色伪码出现在黑色码值0和白色码值1的中间，且对应的像素数量远远小于一个正弦条纹周期对应的像素数量。因此，可以通过判断当前的码值1左边的码值是否为0或者2找到灰度边界，然后设置远小于一个正弦条纹周期的像素数量的阈值将灰色伪码去除，得到最终的两幅三灰度编码图像。

2.2.4 三灰度编码值解码

通过三灰度编码图像的编码值来确定展开相位级次。图5为空间邻域解码图，第一行对应相位级次，第三行和第四行的码值组合成第二行的编码值，通过空间相邻的三个编码值确定相位级次。其中，编码值00，01，02，20，21，22对应的相位级次通过当前编码值和后两个相邻编码值来确定，编码值10，11，12对应的相位级次通过当前编码值和前两个相邻编码值来确定，通过确定的相位级次对包裹相位进行展开得到展开相位。在实际测量时，只需将每行的第一个条纹周期的相位级次通过空间相邻的三个编码值确定即可，当第一个条纹级次确定后只需依次判断下一个编码值是否正确即可确定下一个条纹级次，解码过程简单。当发生编码值跳变时，可以通过空间相邻的编码值来避免编码值错乱，因而本方法适用于非连续表面的测量。

图5 空间邻域解码图Fig.5 Spatial neighborhood decoded image

2.3 错误相位点去除

三步相移算法计算出的包裹相位值受到反正切函数的影响，被包裹在[-π，π]之间。要想得到连续的展开相位，需要利用展开相位级次对包裹相位进行展开，然而编码值边缘处并不能和包裹相位的2π相位跳变处对准。因此，在相位展开时，相位级次和2π相位跳变处会出现对准误差，展开相位存在错误相位点。

错误相位点去除流程如图6所示，通过相邻的两个展开相位点进行一阶差分运算得到相邻展开相位差分值，相邻展开相位差分值设置阈值，找到错误相位点参与差分运算的位置，图7中用圆圈标记出的点。根据实际测量情况，没有对准误差时，展开相位是连续分布的，两个相邻展开相位点的差分值对应在0弧度附近；存在对准误差时，相邻的展开相位点会存在一个相位级次的跳变，相邻展开相位点的差分值会出现如图7所示的两种情况。其中，绿色相位点的差分值对应在2π弧度附近，蓝色相位点的差分值对应在0弧度附近，红色相位点的差分值对应在-2π弧度附近。图7（a）中红色点为正确相位点和错误相位点的差分值，绿色点为错误相位点和正确相位点的差分值，绿色点处为错误相位点位置。图7（b）中绿色点为正确相位点和错误相位点的差分值，蓝色点为错误相位点和错误相位点的差分值，红色点为错误相位点和正确相位点的差分值，蓝色和红色点处为错误相位点位置（彩图见期刊电子版）。

图6 错误相位点去除算法流程Fig.6 Flowchart of wrong phase point removal algorithm

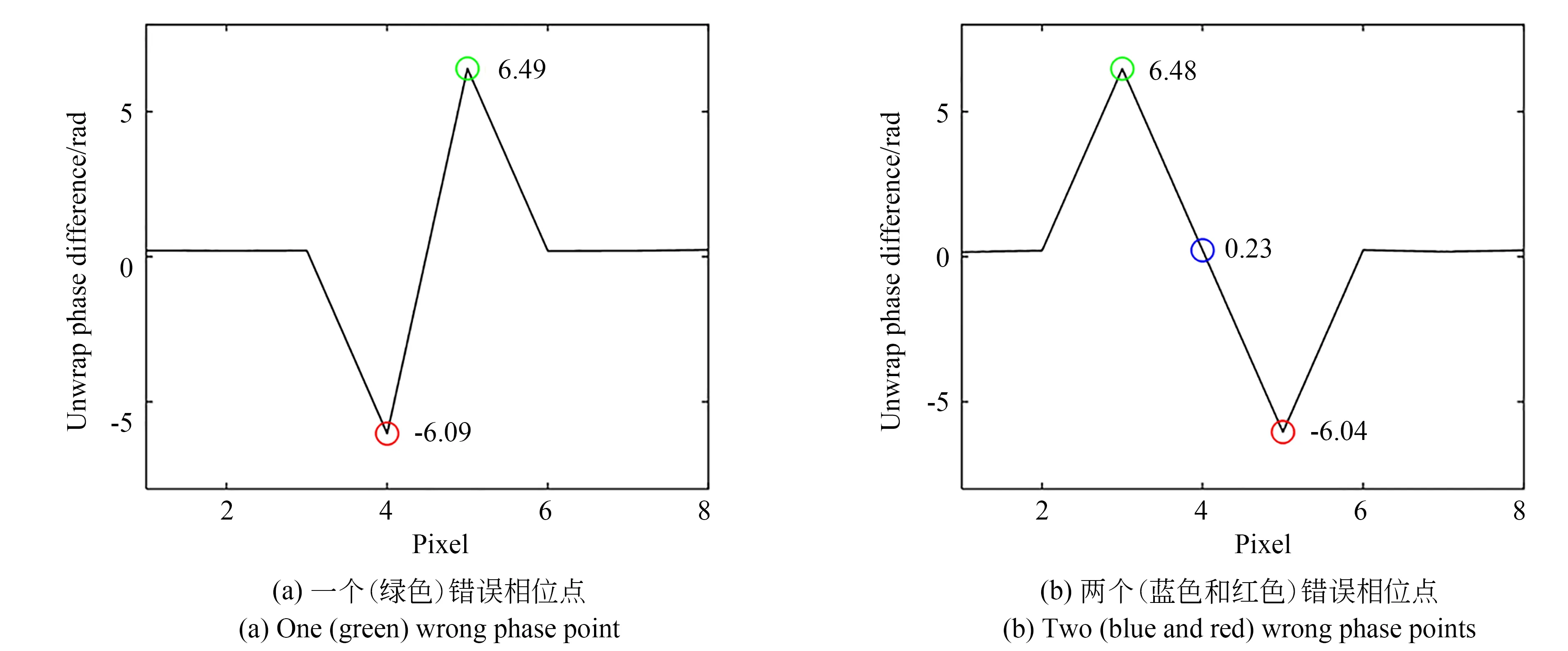
图7 错误相位点的两种情况Fig.7 T wo cases of wrong phase point

错误相位点参与差分运算位置处的相邻展开相位差分值的和小于2 rad作为判断条件，即存在一个错误相位点或存在两个错误相位点。没有对准误差的情况下，展开相位连续分布且单调递增，相邻展开相位的差值在0 rad附近，满足判断条件的错误相位点位置处，分别进行除去错误相位点的1×3均值滤波处理得到最终的展开相位。图7（a）中，绿色点处的相位值通过红色点处的相位值以及其前一个位置的相位值和绿色点处后一个位置的相位值进行1×3均值滤波得到。图7（b）中，蓝色点出的相位值通过绿色点处的相位值以及其前一个位置的相位值和蓝色点处后两个位置的相位值进行1×3均值滤波得到；红色点出的相位值通过绿色点处的相位值以及其前一个位置的相位值和红色点处后两个位置的相位值进行1×3均值滤波得到。

2.4 深度标定

将标定板在几乎垂直于相机光轴的方向上摆放N个已知的位置。在每个位置上投影仪投射12幅正弦相移条纹图到标定平板表面，使用四步相移法计算包裹相位，最佳三条纹选择法［14］计算展开相位，最后选择中间的某一个位置为参考位置，通过式（5）建立了Δz(x，y)和Δφ(x，y)之间的对应关系，拟合每个像素点的相位和深度间的多项式系数作为标定系数。

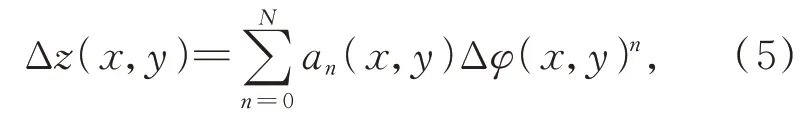
其中：n=0，1，...，N，Δz(x，y)代表测量位置与参 考 位 置 的 距 离，系 数a0(x，y)，…，an-1(x，y)，an(x，y)代 表 多 项 式 拟 合 系 数，Δφ(x，y)代表被测相位与参考相位的变化。

3 实验及结果分析

为了验证本文提出的三灰度编码相位展开方法，搭建了一个硬件系统由LightCrafter4500数字投影仪（912×1 040 pixel）和AD-080GE双传感器棱镜式面阵扫描相机（1 024×768 pixel）组成，实验系统如图8所示。实验中，投影仪投射的正弦条纹周期数是40，相机采用单色模式，相机由投影仪的触发信号同步，测量物体结果如图9和图10所示。

图8 三灰度编码相位展开实验系统Fig.8 Experimental system for ternary-gray encoded phase unwrapping

用所提出的三灰度编码相位展开方法结合三步正弦相移测量一个非连续台阶。相机采集的正弦相移条纹图像对应图9（a）。采集三灰度编码图像对应图9（b）。通过三灰度解码获得的展开相位级次对包裹相位进行展开，得到的展开相位局部放大图如图9（c）所示。三灰度编码得到的相位级次与包裹相位的相位跳变处存在对准误差，展开相位中的错误相位点如图9（d）红色点所示。去除无数据的相位点后，展开相位具有135 256个相位点，展开相位具有1 383个错误相位点。对准误差产生的错误相位点可以通过2.3小节中所提出的方法进行去除，对准误差去除后的展开相位局部放大图如图9（e）所示。最后，通过系统的标定系数重建标准台阶面，得到的三维轮廓如图10所示。每个恢复的标准台阶面上选取所有的像素点进行平面拟合，计算两个相邻的拟合台阶面间高度作为测量值，标准台阶面通过三坐标测量机的测量值作为真实值。相同的测试环境和测量系统，相机采集12幅最佳三条纹图像进行相邻台阶高度的测量，本文所提方法的测量值与最佳三条纹选择法的测量值对比如表1所示。本文所提方法与最佳三条纹选择法的精度相当。本文所提方法只需投射和采集5幅条纹图像，相较于最佳三条纹选择结合四步相移法测量速度提升了2.4倍。实验结果表明，三灰度编码结合三步相移的测量方法能够在快速测量的同时保证测量精度。利用最佳三条纹方法和本文所提方法测量了猫的石膏像，进行了三维形貌恢复。最佳三条纹选择法测量的猫石膏像和面部局部放大图如图11（a）～11（b）所示，本文所提方法测量的猫石膏像和面部局部放大图如图11（c）～11（d）所示，可以看到两种测量方法恢复的猫石膏像的胡须、眼睛和鼻子的细节部分具有同样的效果。由此可以看出，本文提出的方法在恢复物体的细节方面具有良好的表现。

图9 本文方法对标准台阶的测量结果Fig.9 Measurement result of standard step by our method

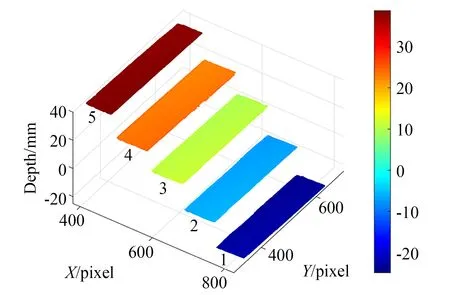
图10 台阶平面Fig.10 Step plane

表1 标准台阶平面的测量结果Tab.1 Measurement results of standard step plane （mm）

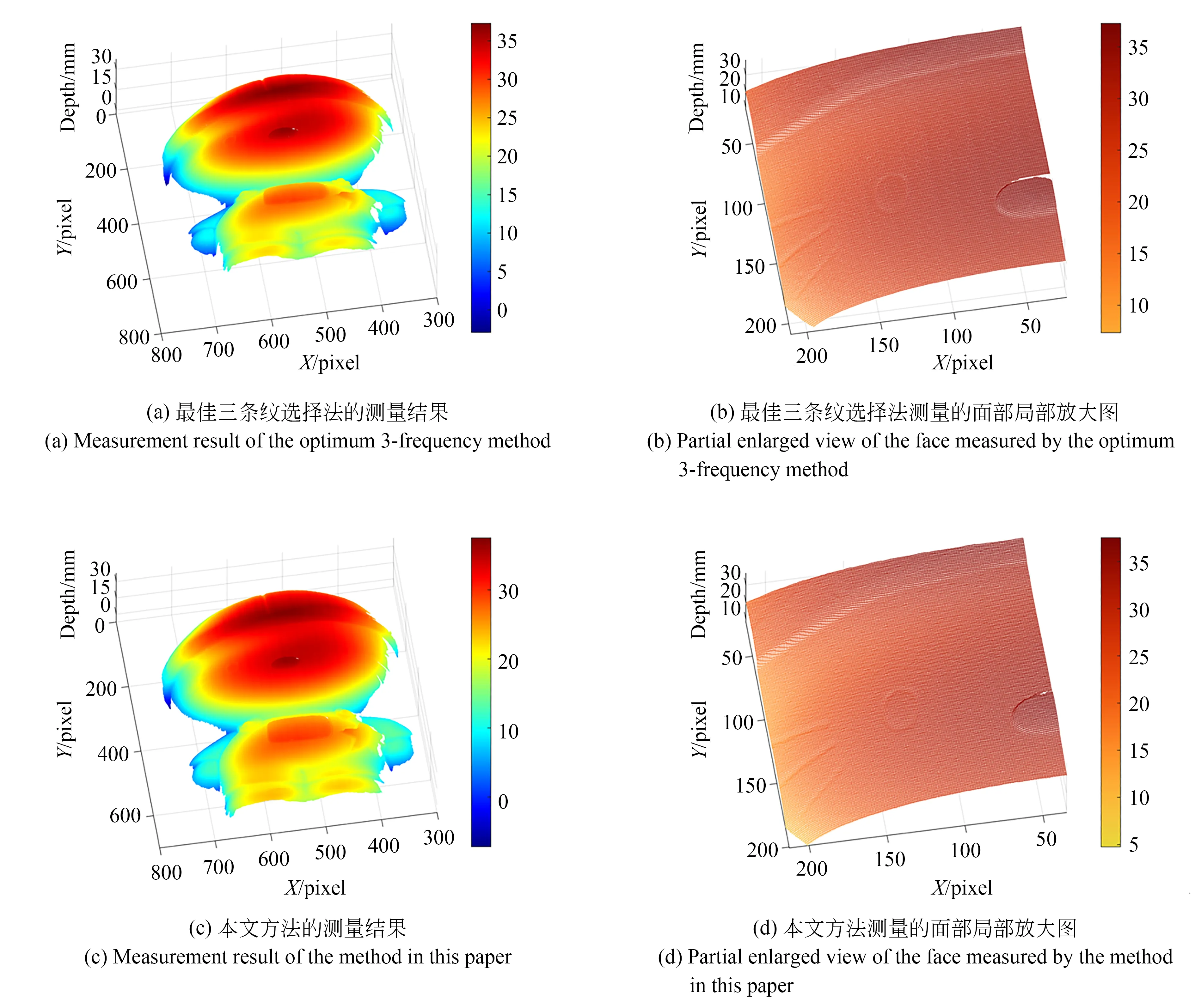
图11 猫石膏像的测量结果Fig.11 Measurement results of cat plaster

4 结 论

本文提出了一种利用空间邻域信息的三灰度编码相位展开方法，该方法通过减少投影和采集的条纹图像数量，可以有效地提高三维测量速度。该方法编码灵活性高，可以生成不同编码图像。将三步相移条纹图像和三灰度编码图像结合对非连续台阶进行测量，在相同的测试环境和测量系统下，与最佳三条纹选择法进行了实验对比。使用最佳三条纹选择法测量的台阶表面高度的最大绝对误差为0.033 mm，本文所提方法测量的最大绝对误差为0.039 mm。所提方法仅需投射5幅条纹图像即可进行物体形貌的恢复，在提高测量速度的同时保证了测量精度。最后对猫石膏像进行了测量，实验结果表明，该方法对物体的细节恢复效果良好，能够实现复杂三维形貌的快速测量。