考虑磁致伸缩效应的非晶合金立体卷铁心振动仿真与实验研究
冯月磊, 刘 洋, 李 琳, 杨富尧, 宋文乐
(1. 新能源电力系统国家重点实验室(华北电力大学), 北京 102206; 2. 全球能源互联网研究院有限公司, 北京 102211; 3. 国网河北省电力有限公司沧州供电分公司, 河北 沧州 061001)
1 引言
节能环保、发展绿色、低碳经济已受到人们的广泛重视。非晶合金材料具有高磁导率、低损耗的优异性能,应用到变压器铁心可以显著降低变压器空载损耗,达到节能效果[1]。与一般三相五柱式非晶合金铁心相比,立体卷结构的铁心具有完全对称的磁路,三个铁心框成正三角形排布,结构更稳定,抗短路能力更出色。但在磁场作用下,铁磁材料会产生体积尺寸的变化,而非晶合金材料的磁致伸缩特性要高于传统硅钢材料,使得非晶合金变压器铁心的振动更大,不能忽略其带来的噪声问题。
国内外诸多学者对非晶变压器铁心磁特性与振动特性开展了相关的研究工作。肖晋桦等人[2]对非晶合金铁心内部磁通密度进行了研究分析,得到平面卷铁心的磁特性磁通密度分布规律;文献[3]与文献[4]应用H平衡函数分析了立体卷铁心内部磁场与磁通密度分布规律;朱叶叶等人[5]从磁场与激励电压的关系出发,结合铁磁材料磁致伸缩特性,得到变压器铁心表面振动加速度与激励电压的关系;Tom Hilgert等人[6]考虑材料磁致伸缩作用的滞后性和对频率的依赖性,对磁致伸缩模型进行了改进并验证了模型的准确性;韩天衡等人[7]研究了温度对单相非晶合金铁心磁特性与振动特性的影响;石永恒等人[8]研究了退火对非晶合金磁特性以及铁心磁致伸缩特性的影响;钟星鸣等人[9]对单相非晶合金卷铁心在不同支撑边界条件下的振动特性进行了研究;祝丽花等人[10]研究了夹紧力对非晶合金铁心磁特性以及振动的影响;李岩等人[11]对三相五柱式非晶合金变压器进行了振动噪声的计算分析,得到铁心改进方案;吴胜男等人[12]对磁致伸缩引起的非晶合金铁心振动进行了解析计算,并考虑了影响铁心振动的因素;张志键等人[13]研究了重熔非晶合金带材及铁心在油浸式非晶合金配电变压器中应用的噪音性能;姜益民等人[14]对三相非晶合金变压器进行了建模,分析了振动噪声特性,提出了减振降噪的措施。现在对非晶合金变压器铁心振动特性的研究多集中在单相与三相五柱式铁心,对于采用立体卷结构的新型非晶变压器铁心研究较少,缺少铁心振动的仿真模型与实验数据。
本文基于磁-机械耦合理论,考虑非晶合金磁致伸缩效应,结合非晶合金磁特性曲线,对一台容量为200 kV·A的非晶合金立体卷变压器铁心进行有限元建模仿真,仿真计算了不同激励下铁心表面振动位移,并结合立体卷铁心结构,设计布置了非晶合金变压器铁心振动测点,进行了不同激励下振动实验,对比铁心仿真与实验结果,分析了非晶合金立体卷铁心的振动特性并验证仿真模型的准确性,为立体卷铁心减小振动、降低噪声提供理论基础。
2 电磁振动耦合有限元计算方法
2.1 磁场分析
通常情况下,非晶变压器铁心区域中交变磁场产生感应电场,该电场产生感应电流,而工频交流激励下,位移电流可忽略不计,麦克斯韦方程组可表示为[15]:
▽×H=J
(1)
(2)
式中,H为磁场强度,A/m;E为电场强度,V/m;B为磁通密度,T;J为电流密度,A/m2;t为时间,s。定义矢量磁位A,满足B=▽×A,经过变换可得到求解铁心电磁场的微分方程:
▽×(υ▽×A)=J
(3)
式中,υ为非晶铁心磁阻率,由非晶合金铁心的磁特性曲线得到,如图1所示,磁通密度与磁场强度满足H=υB。

图1 非晶铁心磁化曲线Fig.1 Amorphous iron core magnetization curve
2.2 非晶铁心磁致伸缩效应
非晶合金材料具有各向同性的性质,测量得到的非晶带材磁致伸缩-磁通密度曲线如图2所示,λpp为不同磁通密度下的磁致伸缩峰峰值。由铁心磁致伸缩产生的应变λ可以由下式确定:
λ=λ(B)
(4)
式中,λ(B)为非晶合金磁致伸缩应变关于磁通密度的函数,由磁致伸缩峰峰值-磁通密度曲线得到。

图2 非晶合金带材磁致伸缩峰峰值-磁通密度曲线Fig.2 Amorphous alloy strip λpp-B curve
2.3 铁心振动特性分析
由于立体卷结构的铁心一般采用闭铁心形式,各层带材相互压紧,铁心气隙很少,因此铁心振动的主要原因为非晶合金材料的磁致伸缩效应。采用弹性力学的应力应变关系将磁致伸缩应变等效为磁致伸缩应力,然后作为体载荷进行计算分析,三维应力应变关系如式(5)所示[16]:
σ=Dε
(5)
式中,σ为应力向量;ε为应变向量;D为弹性矩阵,其表达式为:
(6)
式中,Y为弹性材料的杨氏模量;α为弹性材料的泊松比;X与Z表达式如式(7)、式(8)所示:
(7)
(8)
式中,I为三阶单位矩阵。由式(5)~式(8)可以得到磁致伸缩应力,由下式得到磁致伸缩体积力:
▽·σ=-Fv
(9)
式中,Fv为磁致伸缩体积力。忽略铁心的阻尼效应,结构力场微分方程为:
(10)
式中,m为质量矩阵;k为刚度矩阵;u为位移矢量。通过求解式(10),可以计算铁心振动位移,得到铁心整体振动情况。
3 实验与仿真结果分析
3.1 非晶合金立体卷铁心模型
本文依据实际200 kV·A非晶立体卷铁心尺寸,应用有限元计算软件,建立了非晶合金立体卷铁心三维仿真模型,如图3所示。绕组三相对称,铁心框之间没有直接接触,中间设置薄纸板相连,立体卷铁心底面设置为固定约束。

图3 立体卷铁心模型Fig.3 3D wound core model
依据磁通密度理论计算公式,可求得激励线圈施加的激励电压大小。仿真计算所用参数见表1。

表1 仿真参数Tab.1 Simulation parameters
图4(a)与图4(b)分别是激励电压有效值为165 V与220 V立体卷铁心模型在13 ms时刻单个铁心框沿z方向切面的磁通密度分布计算图,从图4中可以得到,在模型的拐角处磁通密度较大,铁心柱与上铁轭内部磁通密度分布较为均匀,磁通密度平均值分别为0.9 T与1.2 T。
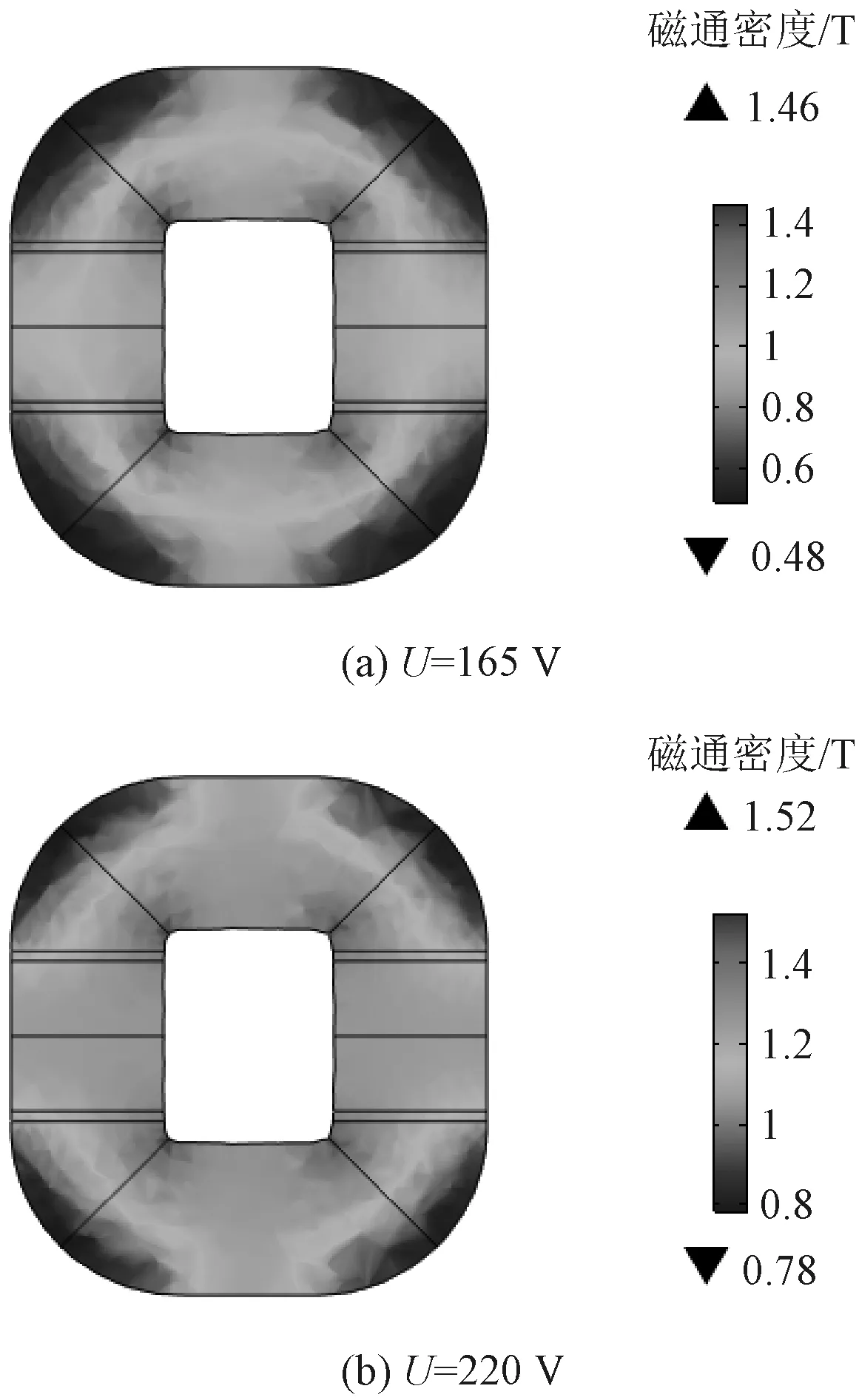
图4 立体卷铁心不同激励电压下磁通密度对比Fig.4 Comparison of magnetic flux density of three-dimensional wound cores under different excitation voltages
在非晶合金立体卷铁心的上铁轭卷绕10匝测量线圈,使用功率分析仪测量感应电压,依据式(11)得到铁心轭磁通密度实验值:
(11)
式中,U2为感应电压值;N2为测量线圈匝数;S2为等效截面积。磁通密度波形比较如图5所示,其中实线为磁通密度B2的仿真结果,虚线为磁通密度B2的实验结果。对比立体卷铁心不同磁通密度的仿真值与实验值见表2。
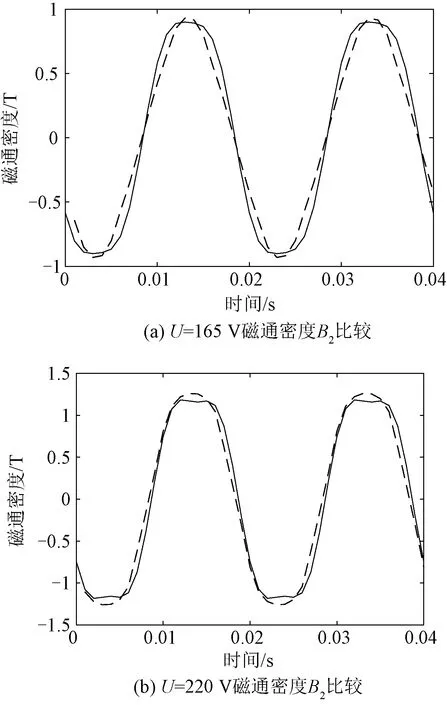
图5 立体卷铁心磁通密度仿真与实验波形比较Fig.5 Comparison of simulation and experimental waveforms of magnetic flux density of three-dimensional wound core
从表2中可以得到,在磁通密度为0.9 T时,仿真值与实验值的波形对比效果较好,磁通密度幅值误差为3.4%;在磁通密度为1.2 T时,由于磁通密度实验值中三次谐波含量升高,仿真值与实验值的波形存在一定差异,但磁通密度幅值相差不大,磁通密度幅值误差为4.8%。该模型可以正确反映立体卷铁心磁特性。

表2 立体卷铁心磁通密度幅值仿真与实验比较Tab.2 Comparison of simulation and experimental magnetic flux density amplitude of three-dimensional wound core
3.2 振动位移仿真与实验结果分析
为进一步研究非晶合金立体卷铁心的振动特性,对一台容量为200 kV·A的非晶合金立体卷铁心进行工频振动实验,激励线圈为25匝,施加的三相交流激励电压幅值与仿真值相同,分别为165 V与220 V。
激励线圈与测量线圈的端口电压使用YOKOGAW公司生产的 WT3000型功率分析仪测量,量程精度为±0.04%,频率范围为0.1 Hz~1 MHz,加速度传感器通过磁吸座吸附到铁心表面,采集的振动信号通过数据采集器显示到计算机上,采样频率为2 kHz,由于立体卷铁心3个铁心框具有完全对称的结构,因此振动测点只需布置在一个铁心框上。根据振动位移仿真分布,可以得到铁心振动由上表面向下逐渐降低,铁心上表面为振动主要位置,因此振动测点主要布置在上表面;由于铁心框内外侧磁路长度不同,与传统硅钢铁心结构相比,立体卷铁心结构更复杂,因磁致伸缩效应使铁心内外侧产生的振动存在一定差异,因此在铁心柱内外表面各布置一个测点,在铁轭侧面布置一个测点。将得到的振动加速度波形经过两次积分,得到测点振动位移波形。实验现场如图6所示,铁心振动测点如图7所示。

图7 振动测点布置图Fig.7 Layout of surface vibration measuring points
图8是激励电压为220 V时,上表面各测点振动位移幅值对比,从图8中可以得到,振动位移在测点②与测点④处振动位移幅值较大,在测点①与测点⑤振动位移相对较小,对比铁心柱测点⑦与测点⑧在不同激励电压下的振动加速度频谱,如图9所示,可以得到,激励电压较低时,测点⑧振动主频为200 Hz,激励电压较高时,振动主频为300 Hz,而铁心柱外部测点⑦振动加速度主频均为100 Hz。与如图10所示仿真振动位移分布相比,可以看到,在铁心上轭,振动最大处发生在上表面近似测点②与测点④的位置,振动位移分布趋势仿真值与实验值相同,振动位移幅值由上表面测点向铁心柱测点减小,与仿真结果相同。

图8 测点振动位移幅值Fig.8 Vibration displacement amplitude of measuring point
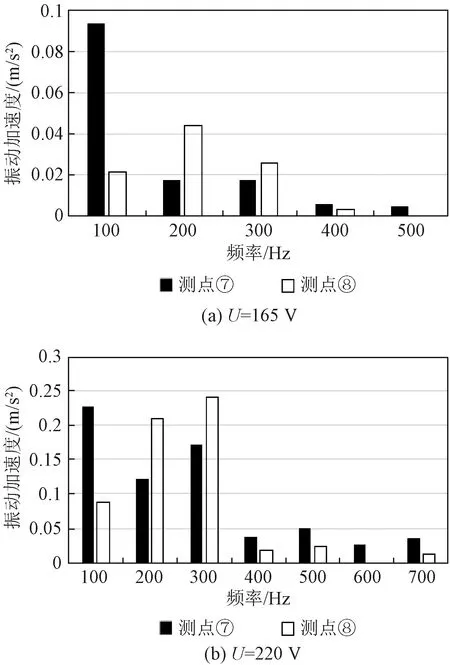
图9 不同激励电压下铁心柱测点振动加速度频谱对比Fig.9 Comparison of vibration acceleration spectrum of iron core column at measuring points under different excitation voltages
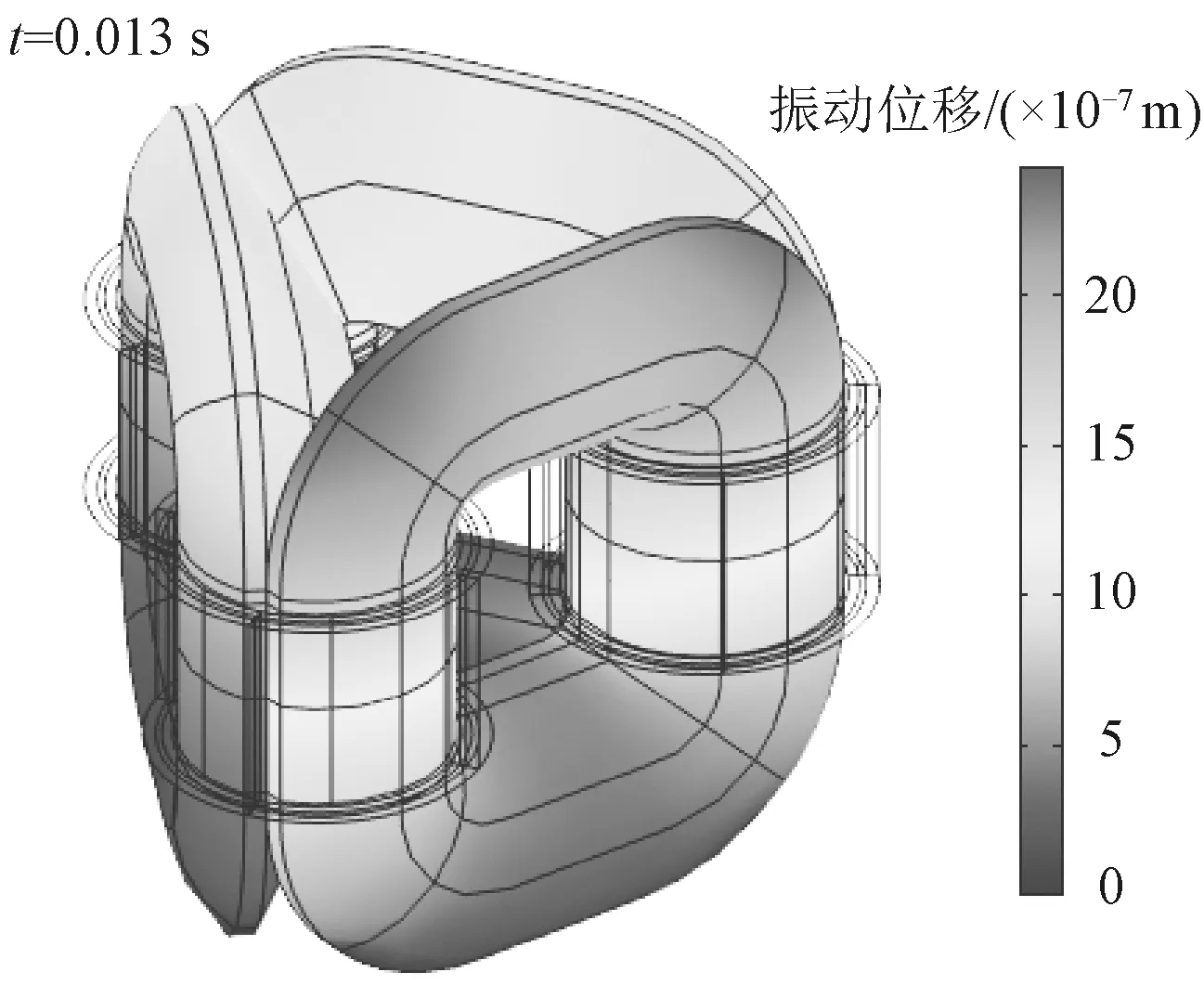
图10 振动位移分布仿真结果Fig.10 Vibration displacement distribution simulation results
选取非晶合金立体卷铁心在激励电压为220 V与165 V情况下不同位置测点(③、⑥、⑦)的振动位移波形进行对比,如图11与图12所示,其中实线为测点振动位移实验值,虚线为测点振动位移仿真值。
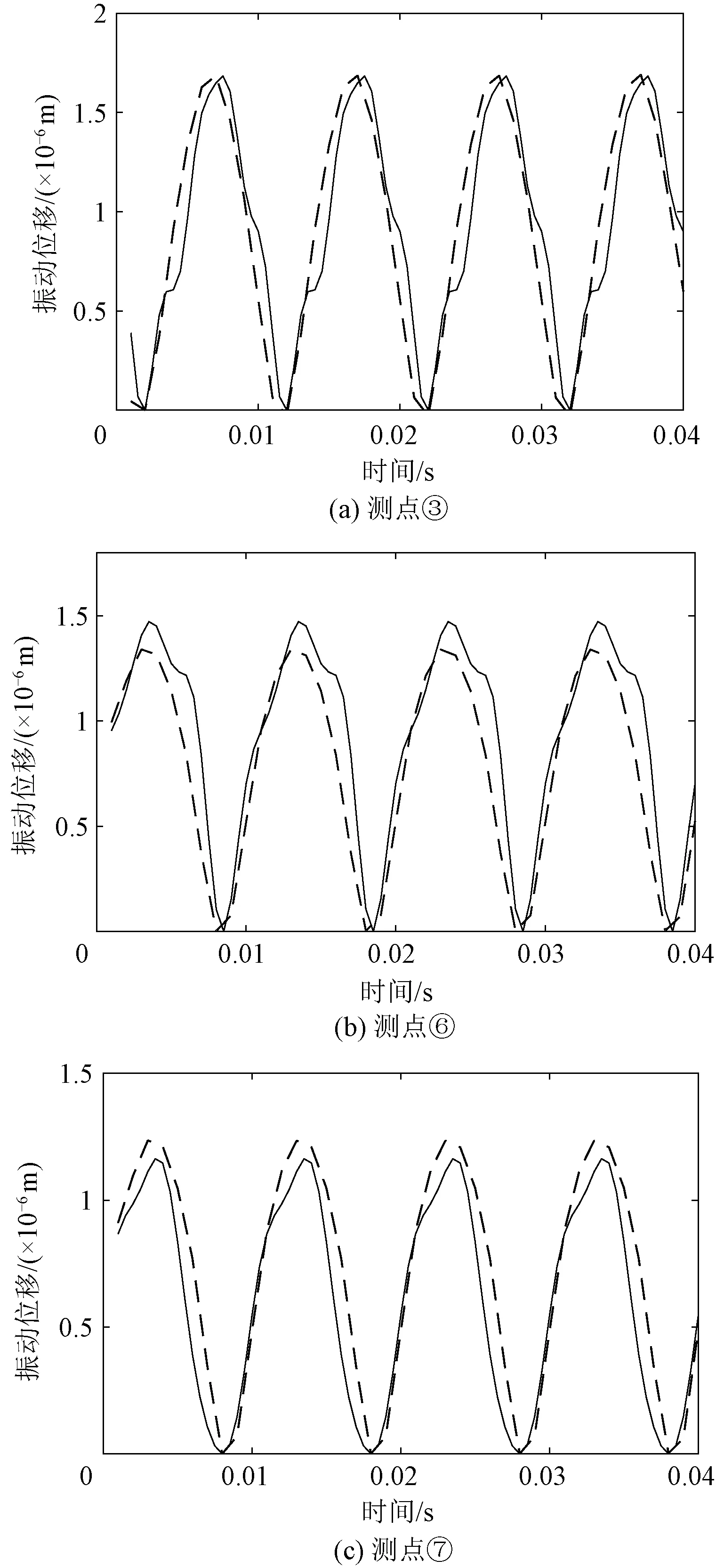
图11 U=220 V 立体卷铁心振动位移仿真与实验对比Fig.11 U=220 V simulation and test comparison of three-dimensional wound core vibration displacement
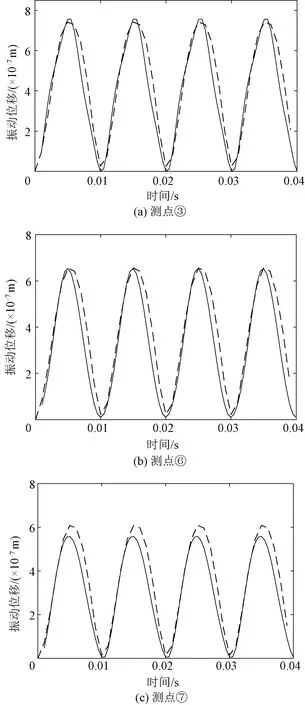
图12 U=165 V立体卷铁心振动位移仿真与实验对比Fig.12 U=165 V simulation and test comparison of three-dimensional wound core vibration displacement
从图11与图12中可以看出,各测点振动位移呈现周期性变化,振动位移主频为100 Hz,随着磁通密度的增大,振动位移频谱出现100 Hz高倍频分量,与传统硅钢变压器铁心振动特性不同的是位于铁心柱测点的振动加速度主频分量,在铁心柱内侧点,振动主频为200 Hz。测点振动位移幅值的仿真与实验对比结果见表3。在磁通密度较低时,仿真与实验的振动位移波形吻合程度较高,当磁通密度较大时,仿真的位移结果与实测的结果趋势相同,幅值较为接近,振动位移波形存在差异,经过分析,原因有以下几点:
(1)振动位移100 Hz分量为振动的主要分量,远大于其他频率分量,100 Hz分量对振动位移的幅值影响最大,仿真与实验的振动位移波形幅值相差不大。
(2)实际立体铁心为卷形结构,铁心为带材一层层卷绕而成,仿真时为了减少模型复杂度,提高计算速度,将铁心模型设置为一个整体,卷形结构会让铁心内部磁通密度产生三次谐波分量,同时,非晶合金材料磁致伸缩的非线性特性也会使铁心的磁通密度产生高次谐波分量,这些谐波分量随着磁通密度的提高,占比逐渐增大。因此在磁通密度为0.9 T时,由于谐波分量占比较少,仿真与实验拟合效果更好,在磁通密度为1.2 T时,从实验位移的频谱波形可以看到,高次频率分量占比较高,仿真与实验的吻合效果要差一些,影响仿真的准确性。
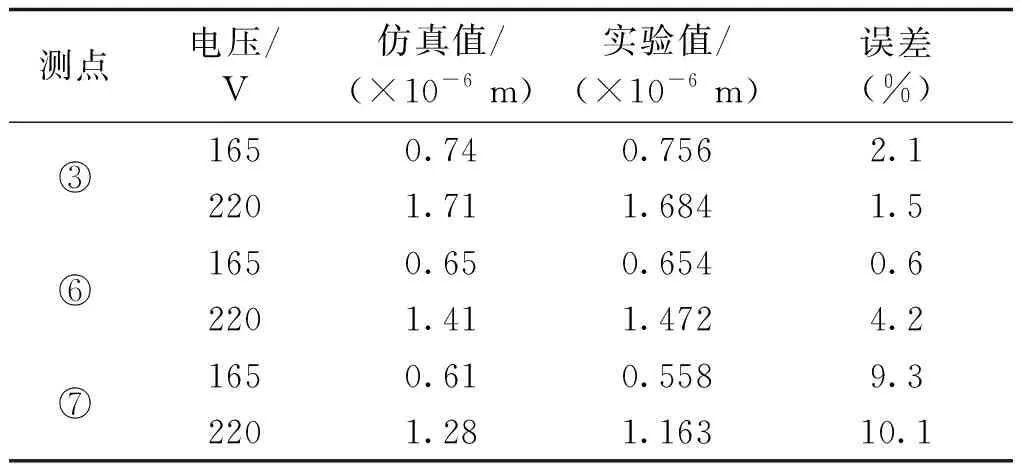
表3 测点振动位移幅值对比Tab.3 Comparison of vibration displacement amplitude of measuring points
(3)仿真时将铁心下表面设置为固定约束,进行振动实验时将铁心置于木板上,不同的边界条件会影响仿真计算的结果。
(4)铁心柱内侧磁路较短,磁通密度仿真分布结果也显示内侧磁通密度较大,在较高激励电压下,铁心柱内侧受材料磁致伸缩非线性特性影响更大,从而出现以200 Hz为主频的振动频谱。
从表3中可以得到,该立体卷铁心模型对于上铁轭测点的振动位移仿真较为准确,误差均小于5%,可以用该模型对不同工况下的振动位移进行仿真,仿真结果表明,立体卷铁心振动主要来源为非晶材料磁致伸缩效应。
4 结论
本文围绕一台三相非晶合金立体卷变压器铁心模型,对其进行了振动实验及三维的电磁机械耦合振动分析。测量了模型在不同激励电压下的铁心内部磁通密度分布和铁心表面振动位移分布,同时仿真研究了该模型在不同激励电压下的磁场分布和非晶合金磁致伸缩作用下的振动位移分布。实验和仿真结果对比表明:由于立体卷铁心与一般平面卷铁心不同,不存在气隙,因此铁心振动的主要原因为非晶带材磁致伸缩力的作用,无需考虑电磁力的作用;立体卷铁心振动主频是激励电压频率的两倍,在额定激励电压下,振动位移高次频率分量占比增大,位移波形发生畸变,铁心柱内侧振动主频与其他位置不同,为200 Hz。铁心振动最大处为铁心上表面,且表面振动位移幅值相差不大,在采取抑制立体卷铁心振动位移时,应优先考虑铁轭位置,频率为100 Hz的振动分量;本研究提出的非晶合金立体卷铁心模型与实验所测数据吻合较好,可以应用于实际立体卷变压器铁心减振降噪措施设计的计算。

