隧道爆破振动信号畸变校正及特征提取研究

付晓强，俞 缙，刘纪峰，黄凌君，戴良玉，康海鑫

(1.三明学院建筑工程学院，福建 三明 365004；2.华侨大学福建省隧道与城市地下空间工程技术研究中心，福建 厦门 361021；3.工程材料与结构加固福建省高等学校重点实验室，福建 三明 365004；4.三明科飞产气新材料股份有限公司，福建 三明 365500)

城市隧道钻爆法施工过程中，产生的爆破振动对周围建(构)筑的负面影响不容忽视[1-3]。开展爆破振动监测是现阶段爆破损伤评价最为重要的手段之一。隧道爆破振动测试过程中，由于爆破近区产生的瞬时能量输入过大，在较强的脉冲能量作用下测试仪器的惯性原件发生强烈振荡，测试输出指标很难保持线性输出[4]。另一方面，若选用的测振仪不匹配导致超量程、仪器未按时进行标定以及测试周围环境的干扰，均会导致隧道爆破监测信号出现不同程度的畸变。

现阶段对于时变信号多尺度自适应分解存在许多算法，如变分模态分解(VMD)、经验模态分解(EMD)、局部均值分解(LMD)和希尔伯特-黄变换(HHT)等，但对于不同信号的处理能力却有所差异[5-6]。其中，变分模态分解由于其预设的尺度和非递归分解模型所具有的自适应能力，在克服模态混叠和增强滤波效果方面具有独特优势。得益于对上述问题的改善，变分模态分解是目前时变信号处理分析中的重要算法之一。同步挤压小波变换算法(Synchrosqueezed Wavelet Transforms，SWT)是由连续小波变换发展而来的高分辨率分析算法，具有良好的时频分辨和信号重构能力，在非线性信号分析中取得了许多的显著成果。

实践证明:爆破近区测试信号发生畸变的概率较远区高[7]。以往对于隧道爆破近区受畸变影响的爆破信号通常直接舍弃，导致测试数据不完整，直接影响到分析结论的可靠性。因此，开展爆破振动信号畸变校正是信号预处理的关键环节。本文中拟采用变分模态分解算法结合同步挤压小波变换，并辅以时频分析对隧道爆破振动信号能量特征进行了分析，探索并建立了隧道爆破振动信号畸变校正和特征提取方法。

1 基本理论

1.1 变分模态分解(VMD)

变分模态分解是将信号分解为k个中心频率为ωk的模态函数uk，uk的具体形式为[8]

uk(t)=Ak(t)·cos[φk(t)]

(1)

式中：Ak(t)为瞬时幅值；φk(t)为瞬时相位，两者均为缓变过程。

VMD算法将信号分解过程转移到变分框架内进行处理，其算法核心包括变分问题的构造及其求解。

变分问题的构造过程如下：

1)对于单个模态分量uk(t)，利用Hilbert变换构造解析信号，通过混合指数解调各自估计中心频率的方法，将各个模态分量的频谱调制到相应的基频带上：

(2)

式中：j为虚数单位；δ(t)为狄拉克函数；ωk={ω1,…,ωK}为经过VMD得到的若干个模态对应的中心频率；uk={u1,…,uK}为分解得到的k个模态分量；*为卷积运算。

2)通过解调信号的高斯平滑度，计算式(2)表示的信号梯度的平方L2 范数，估计获得各模态分量的带宽，构造的变分问题可表述为如下的优化过程，即：

(3)

(4)

变分问题的求解过程如下：

为求式(3)中的约束变分模型，此处引入二次惩罚因数α和Lagrange乘法算子λ(t)，其中α为较大的正数且在高斯噪声存在的情况下可保证信号的重构精度，算子λ(t)使得约束条件保持严格性，构造的增广Lagrange表达式如下：

L({uk},{ωk},λ)=

(5)

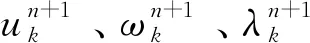
1.2 同步挤压小波变换(SWT)

假定时变信号f(t)的长度为n=2L+1，采样间隔为Δt。令nv=64，取na=Lnv，则：

(6)

(7)

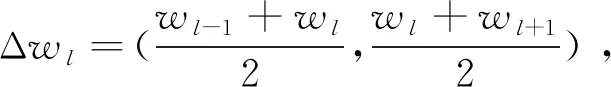
(8)

式中：median为中值函数；Wf(a,b)为信号f(t)连续小波变换得到的小波系数；a为尺度因子；b为平移因子。则在中心频率wl上SWT值Tf(wf,b)为

(9)

式中：(Δa)i=ai-ai-1。

同步挤压小波反变换为

(10)

通过同步挤压小波反变换可重构任意频率区间信号分量，从而实现所关心的频率区间信号完全无损重构过程。

2 工程概况

青岛地铁隧道3#线采用钻爆法施工，该隧道掘进断面30.8 m2，跳段选用MS1～MS13范围内共7个段别毫秒电雷管[10-11]，具体炮孔布置如图1所示。

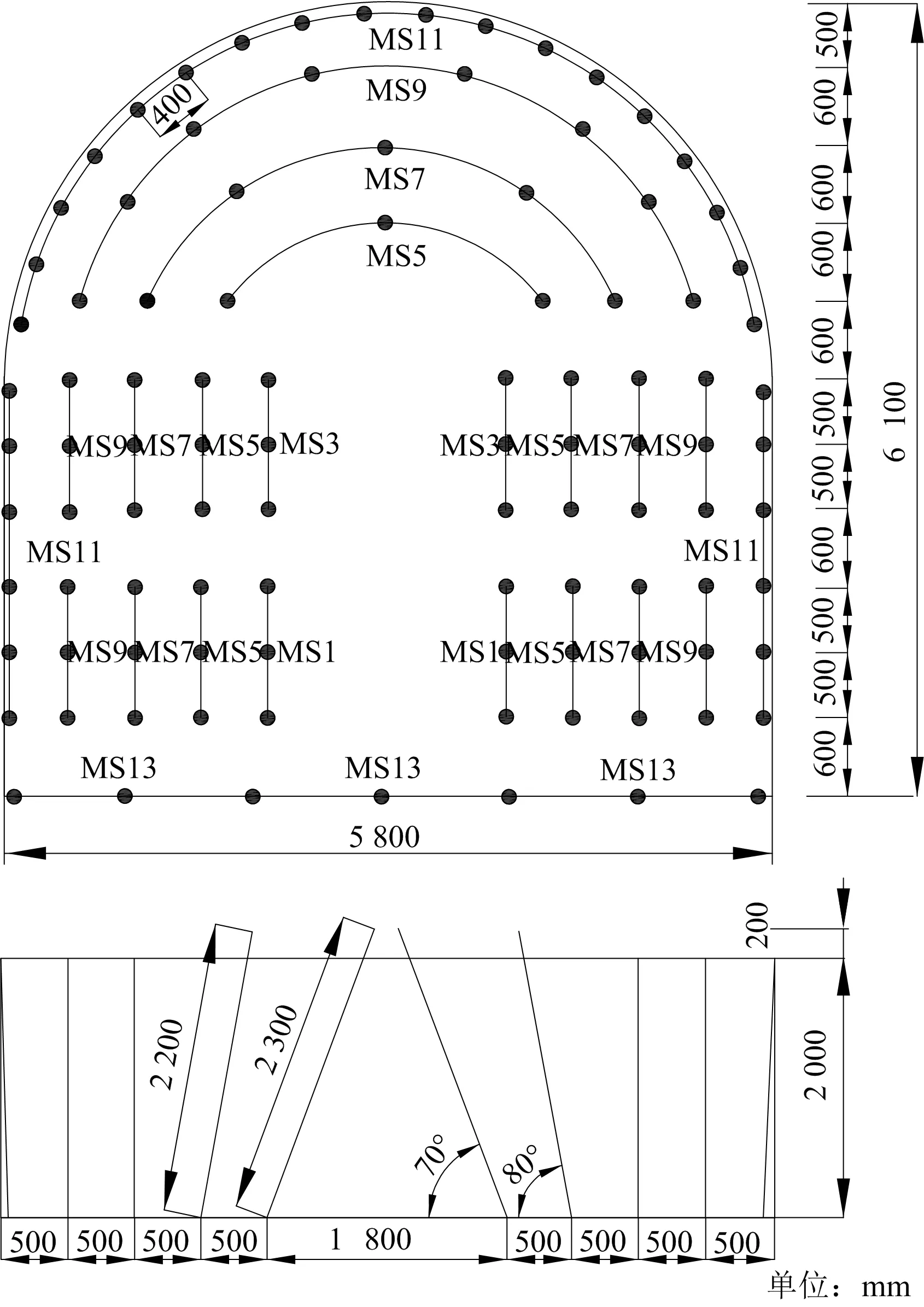
图1 炮孔布置参数

隧道测试段埋深22 m，岩性以中砂岩为主，普氏系数4～6，采用全断面开挖，单循环起爆总药量为66.9 kg。其中，掏槽孔24个，按照炮孔位置选用MS1、MS3、MS5段雷管，对应起爆药量分别为7.2、7.2、10.8 kg；辅助孔40个，选用MS5、MS7、MS9段雷管，单孔装药量均为0.6 kg，对应起爆药量分别为1.8、10.2、12 kg；周边孔30个，采用MS11段雷管配合导爆索起爆，单孔药量为0.45 kg，起爆药量为13.5 kg；底孔7个，MS13段起爆，单孔装药量0.6 kg，共4.2 kg。

为了客观评价该爆破方案下产生的爆破振动效应，对隧道掘进过程中地表产生的振动进行了监测。为了避免隧道已开挖段产生的“空洞效应”对测试数据的影响，测点选择在隧道掌子面前方地表2 m处，测点布置如图2所示。

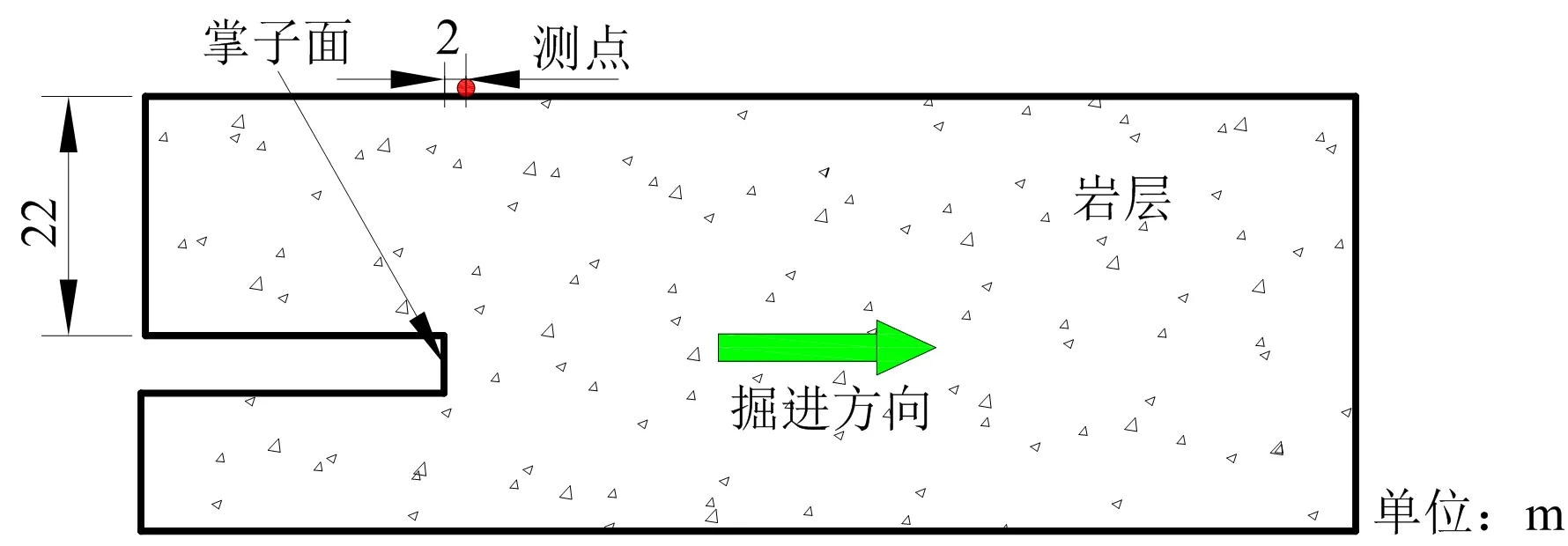
图2 测点布设

3 难点分析

测试选用中科测控TC-4850型爆破振动测试仪，在隧道上方地表选择固定的监测位置并提前浇筑好测振平台，测振仪固定时首先清理平台表面浮灰，采用石膏粉加水搅拌至糊状粘贴传感器探头，这一过程中调整水平气泡处于标准水平位置，待探头与平台表面粘贴牢靠后根据工程特点设定采样频率为8 kHz，采样时长为1.5 s并使主机处于待触发状态。测试过程中将测振传感器的x向指向隧道开挖中轴线方向，z向与x向垂直且两者位于水平面内，y向与x、z向垂直并指向地表，传感器三向按照笛卡尔坐标系布置，可同时获取3个方向的爆破信号波形曲线，三向振动波形曲线具体如图3所示。其中，x向波峰值为2.02 cm/s，波谷值为-1.33 cm/s，峰峰值差为3.35 cm/s，主频为32.26 Hz；y向波峰值为1.07 cm/s，波谷值为-0.67 cm/s，峰峰值差为1.74 cm/s，主频为3.49 Hz；z向波峰值为2.02 cm/s，波谷值为-1.50 cm/s，峰峰值差为3.52 cm/s，主频为38.84 Hz。水平x、z向波峰、波谷值及峰峰值差较为接近且出现的时刻一致(30 ms以内)，主频值相当，而垂直y向波峰、波谷值出现的时刻在时间轴上明显离散，波峰值出现在21.19 ms，而波谷值出现在741 ms左右，主频值出现较大偏差，与隧道爆破振动特征严重不符，出现了明显的失真。同时注意到，图3中三向信号波形均不同程度出现了偏离基线中心位置的漂零趋势项，尤其是垂直y向，信号的波动形态完全淹没在干扰成分中，信号失真导致其奇异性增强，因此，预处理过程中对畸变信号进行校正是极为必要的。

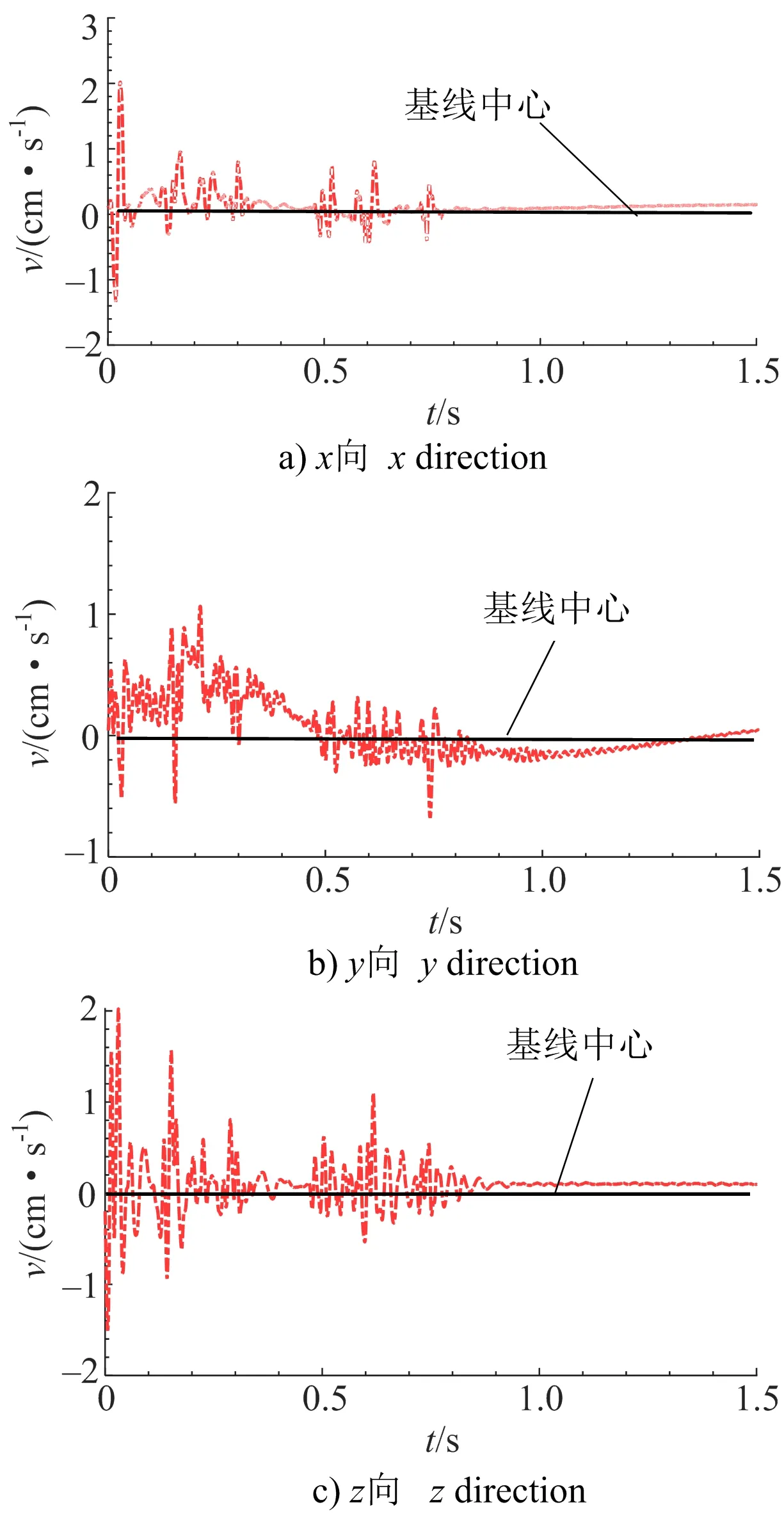
图3 典型畸变爆破振动信号

由于测试环境的复杂性及仪器自身的原因，隧道爆破监测信号通常会发生畸变，影响信号后续的特征提取及参数调整优化过程。另一方面，分析过程中各环节产生的误差会不断累加，从而导致分析结果精度较差，不能客观反映爆破振动实际情况。

4 方案设计

本文针对隧道爆破振动畸变信号的奇异性，利用变分模态分解消除信号中的趋势项，通过同步挤压小波变换重构优势频段信号，彻底解决了信号扭曲引起的特征失真问题。具体实现步骤如下：

1)根据待分析信号采样频率和采样长度等参数，确定VMD分解中惩罚因子α取值，分解层数k统一确定为2；

式中，ldi为第d次仿真试验中目标回波i是SST，D为蒙特卡罗试验次数，N1为第d次仿真分析得到的目标回波个数。

2)信号VMD分解得到的第二阶模态分量便是消除趋势项后的校正信号f′(t)；

3)同步挤压小波对步骤2得到校正信号f′(t)进行时频分析，得到校正信号f′(t)能量在时频域上的分布，从而确定信号的优势频率区间；

4)根据校正信号时频谱中的优势频率区间范围，利用同步挤压小波变换优良的信号重构能力，重构得到反映信号特征的真实信号；

5)重复上述步骤1～4，得到了同一测点三向分量信号的优势频率重构子信号f″(t)，并求取其三向矢量和；

6)根据矢量和峰值点时刻，辨别雷管段别并提取瞬时、边际能量特征。

4.1 趋势项消除

变分理论认为，当时变信号中趋势项的频谱中心频率位于5 Hz内时，则VMD分解得到的第一阶模态分量便为信号中的趋势项[12]。变分模态分解中的两个重要参数分别为：惩罚因子α和分解层数k，其中α取值决定了信号分解精度，通常α取为待分析信号采样长度的2倍。同时，文献[5]中也表明含有显著趋势项的时变信号经过VMD分解后得到的第一阶模态分量即为趋势项，与分解层数k无关。为了提高运行效率，设置分解层数k为2。此处，设置α=24 001(信号采样长度为12 001)，对图3中信号进行VMD分解，相应的信号分解结果及其功率谱分别如图4和图5所示。

图4 VMD算法趋势项提取结果

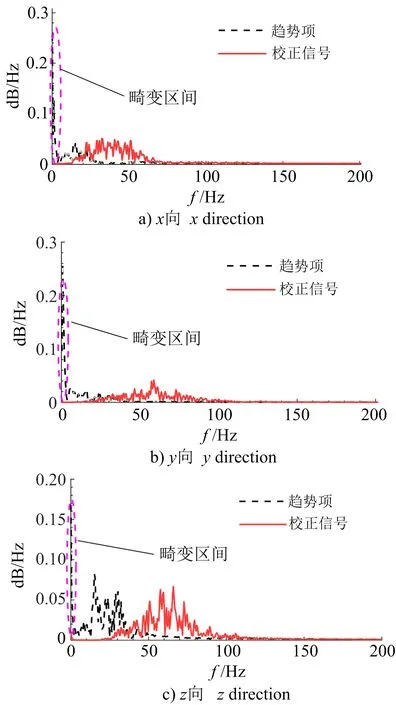
图5 不同信号成分功率谱分布

VMD分解后得到的校正信号波形光滑，波峰波谷值沿基线中心近似对称分布。其中，x向波峰值为1.42 cm/s，波谷值为—1.41 cm/s，主频为52.78 Hz；y向波峰值为0.45 cm/s，波谷值为—0.48 cm/s，主频为58.59 Hz；z向波峰值为1.17 cm/s，波谷值为—1.25 cm/s，主频为57.61 Hz。趋势项和校正信号的功率谱在频率轴上实现了有效分离，说明通过变分模态算法进行爆破信号畸变校正是切实可行的。校正后的信号主频接近并保持相对稳定，同时应注意到三向振速从大到小依次为：x向>z向>y向，频率从高到低依次为：y向>z向>x向，与振速幅值变化趋势相反，说明隧道爆破振速越大，则主频越低，揭示了隧道爆破峰值振速与主振频率之间的定性关系。同时应注意，对同一信号进行多次重复校正易导致信号信息缺失，在工程实践中应以满足分析要求为原则来综合确定相关参数取值，避免过度校正引起的特征指标损失。

4.2 爆破信号重构

从校正信号的时频谱(见图6)可以看出，三向信号均具有初始频带范围宽泛、高频衰减较快的特点。水平x向(径向)频率中心为32 Hz，能量在20～70 Hz频率区间出现聚集；水平z向(切向)频率中心为64 Hz，信号在30～80 Hz区间有能量聚集；垂直y向(竖向)频率中心为64 Hz，信号能量主要集中在30～80 Hz频带范围。因此，对上述能量聚集频率区间内的信号进行重构，能够准确把握隧道爆破振动信号的特征信息。利用同步挤压小波变换可重构任意频率区间信号的优良特性，对上述各自所对应频带重构得到能够反映爆破特征信息的真实信号(见图7)。

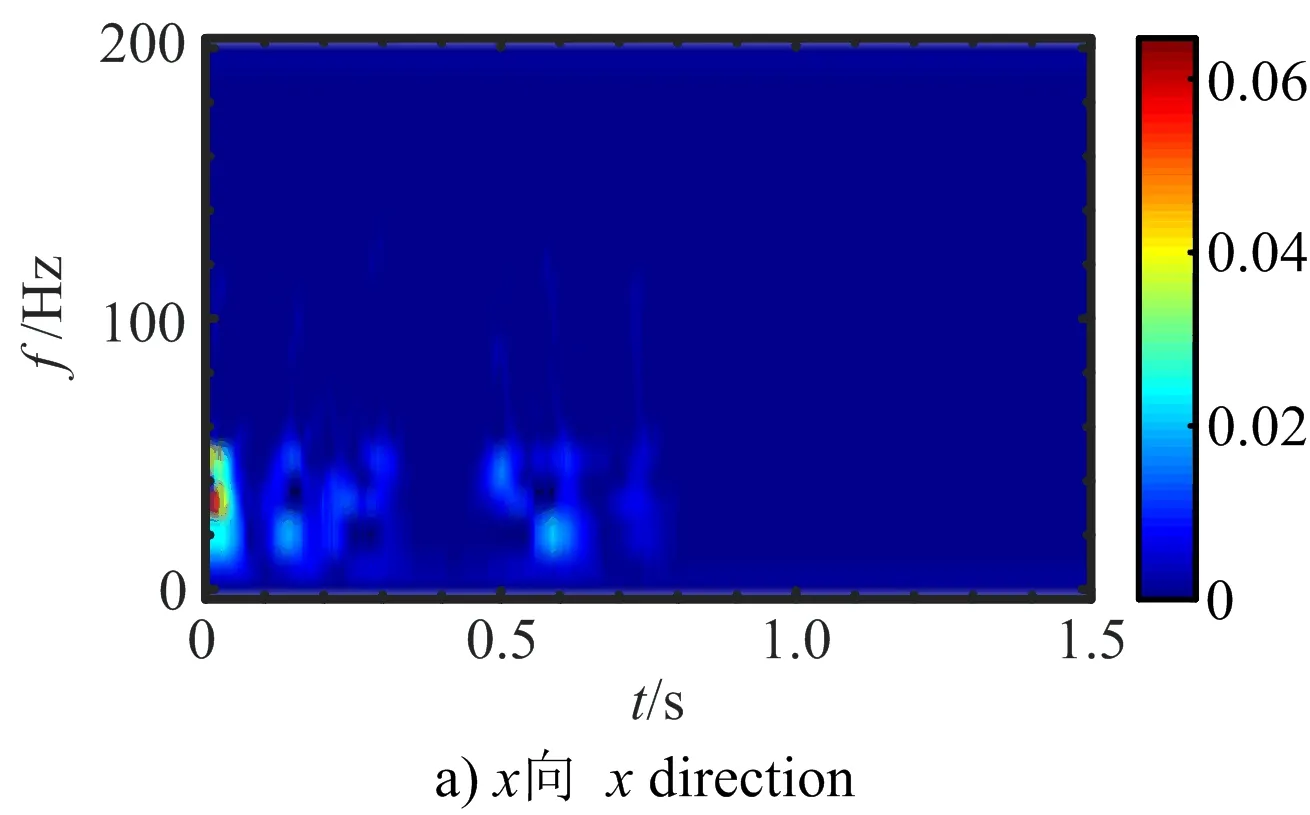
图6 校正信号时频谱

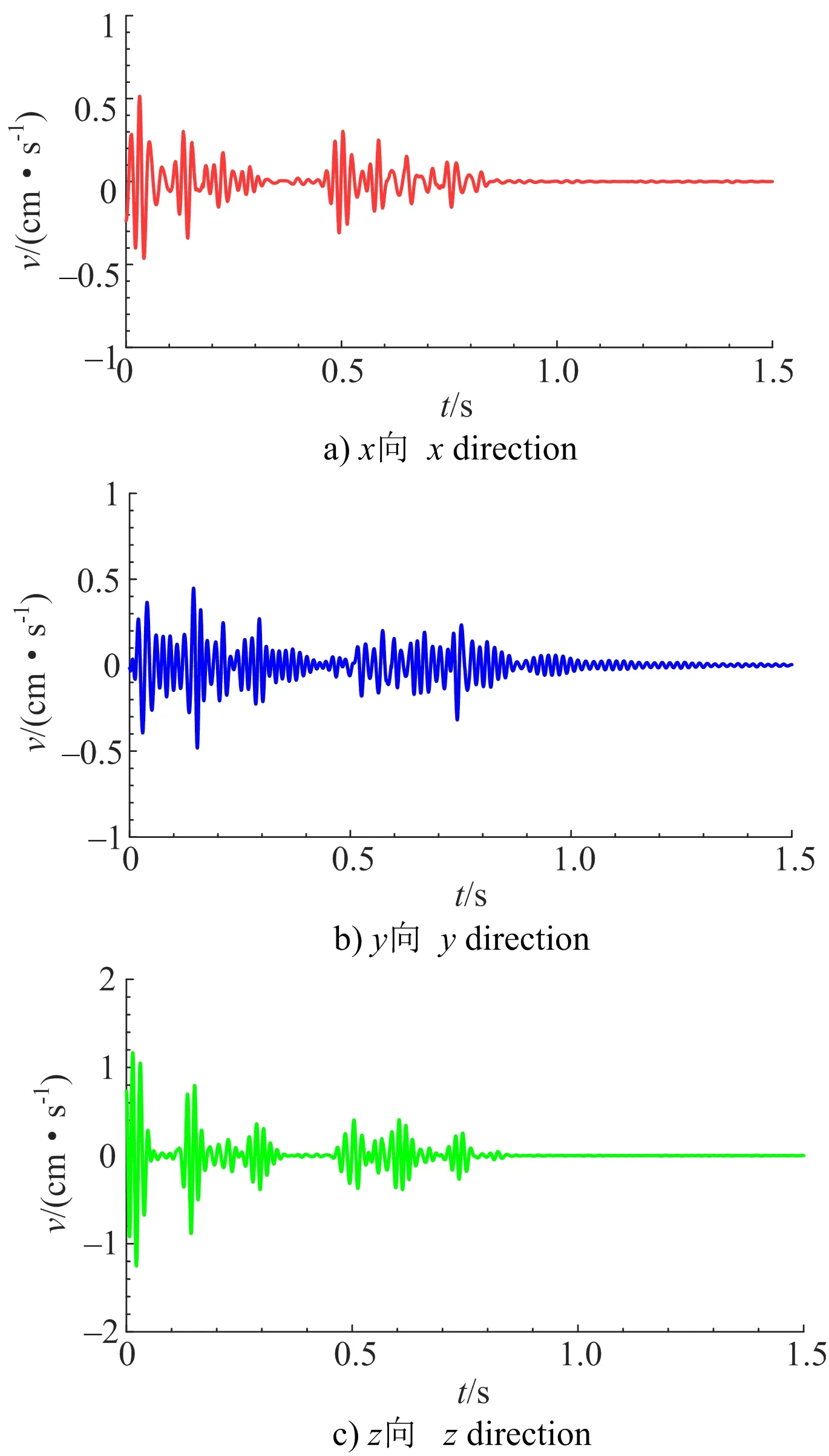
图7 同步挤压小波变换重构信号

通过同步挤压小波变换重构后的时域信号波动稳定，较好地继承了信号的主要变化特征，具有很好的细节保持能力。同时，在主振时域(0.8 s)后，信号波动迅速减缓并逐渐回归到基线零点附近，具有很好的去噪能力，信号重构效果优良，精度满足分析要求。

5 结果与讨论

5.1 分析结果

采用三向振速矢量合成速度作为指标对爆破振动进行评价，更能体现爆破对周围建(构)筑物损伤的综合作用。矢量合成振速v矢的具体表达式为

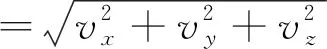
(11)

式中：vx为x向振速，cm/s；vy为y向振速，cm/s；vz为z向振速，cm/s。

原信号矢量合成、三向振速进行矢量合成后的振速曲线及其时频面上的能量分布如图8a、图8b和图8c所示。

与原始信号矢量合成曲线(见图8a)相较可知：由于原始信号存在畸变导致矢量合成振速受到污染，合成曲线出现虚假峰值，信号特征辨识度差。校正重构信号矢量合成振速曲线连续光滑，信号噪声及干扰均得到了很好地抑制，所用雷管段别与爆破方案一致，时频谱上各段别雷管起爆时刻清晰可辩，验证了上述组合算法的可靠性。

对信号的时频分布函数进行频率轴上积分得到信号的瞬时能量谱(见图9)，量纲为J/t。由于不同方向采集到的爆破振动波的类型有所不同，x和y方向构成的平面代表瑞利波(Rayleigh wave)的质点运动，x和z方向代表勒夫波(Love wave)的质点运动[15]。由瞬时能量分布可知，水平x向的振动能量幅值率先到达，垂直y向能量峰值到达时刻有一定的延迟，水平z向具有多个能量峰值。隧道爆破引起的振动中，Love波率先被探头接收，Rayleigh波相对有约为0.03 s的时延。

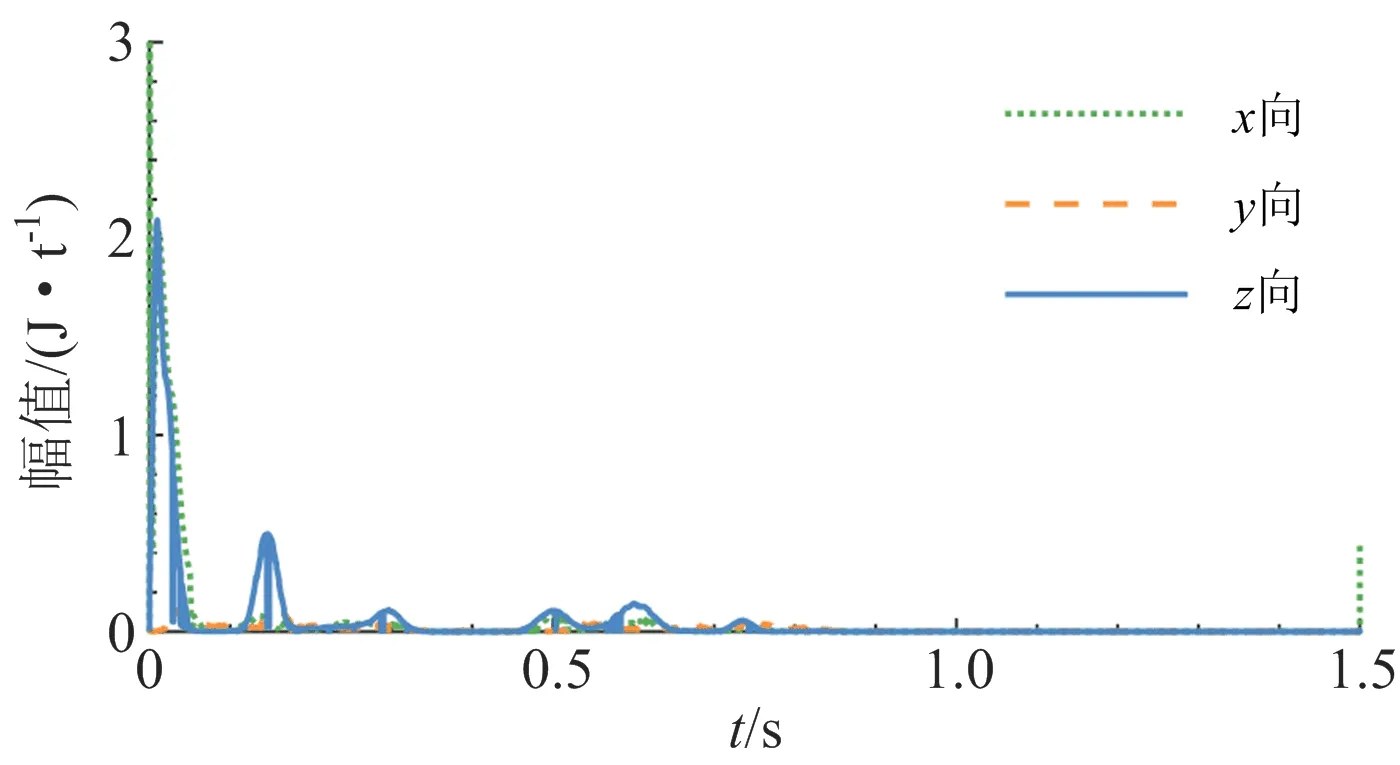
图9 信号瞬时能量谱

对时频分布函数进行时间轴上积分便得到了信号的边际能量谱(见图10)，量纲为J/Hz。频率边际谱表征了信号不同频率成分在时间全局上的累加，与功率谱的不同在于边际谱可准确描述频率成分在整个振动过程中的能量占比权重[16]。由图10可知，垂直y向和水平z向能量频率中心均为64 Hz，这与图6中其时频谱的能量聚集中心处的频率是一致的。水平x向由于同时受Love波和Rayleigh波的影响而具有多个频率中心，能量频率中心分别为32 Hz和48 Hz。在边际谱中48 Hz处有较强能量峰值而在图6a中时频谱中并未出现较强的能量聚集，说明x向能量在此频率处聚集但在时间上并不集中，这种频带窄但作用时间长的特殊能量加载形式也需高度重视，防止产生损伤累积效应。边际能量分布表明：对于该地质地形条件下的隧道爆破振动效应的控制，应密切关注20～80 Hz范围内的能量分布变化，以防造成安全事故。

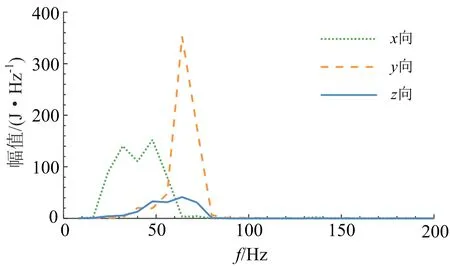
图10 信号边际能量谱

5.2 讨论

针对隧道爆破畸变信号开展分析，由于不同爆破工程产生的振动信号存在一定差异，在分析过程中应根据工程特点对相关参数进行调整，以达到最优化的分析效果。在后续研究过程中，笔者会重点分析多种不同类型的爆破信号畸变特征及针对性的优化措施，以期得到更具普适性的分析方法。

6 结论

1)隧道爆破信号中趋势项是导致信号产生畸变的首要原因，隧道爆破测试过程中应选用高精度、宽频量程的测振仪并对仪器相关参数进行合理设置，尽可能采用无线网络传输形式进行信号采集和传输，避免测点频繁布置导致的位置偏差。长线隧道测试过程中，应缩短测试仪器的常规标定周期，提高信号测试精度，从根源上避免信号畸变的产生。

2)隧道爆破信号的低频畸变成分主要位于5 Hz以下，而现阶段广泛使用的测振仪工作频率均大于5 Hz，致使测试信号中低于5 Hz部分信号波形难以保持线性输出，导致信号产生低频畸变。同时受测试环境复杂度影响，隧道监测信号中亦普遍包含高频噪声(200 Hz以上)，测试信号畸变引起的奇异性和噪声干扰对于信号特征提取会产生不利影响，在信号深入分析过程中必须预先进行校正和消噪。

3)变分模态分解算法在设定合理参数前提下，可有效提取出信号中的畸变趋势项成分，从而得到校正后的特征信号。从特征信号时频谱确定其能量聚集频率区间，利用同步挤压小波变换可获得重构选定频带的真实信号。三向真实信号的矢量合成曲线峰值数量与选用的雷管段别有对应关系，组合算法对畸变信号的处理效果好，自适应性强，适合用于隧道爆破及类似工程畸变信号的批量预处理。