土-构耦合效应对15 MW风力机地震动态响应的影响

梅 轩， 杨 阳

(1.同济大学 土木工程学院，上海 200092；2.宁波大学 海运学院，浙江宁波 315211)

为实现“碳中和”的能源发展战略目标，我国计划大力发展太阳能和风能等可再生能源。2021—2030年海上风电计划装机容量达6.5 GW，2060年风电总装机容量将突破200 GW[1]。由于特殊的地理位置，我国环渤海及东南沿海等风能丰富地区易受到地震灾害的影响。为保证海上风电结构安全和可靠运行，需研究复杂环境下大型海上风力机地震动态响应特性。

早期关于地震对风力机动力学特性影响的研究主要针对陆上风力机。如2005年Witcher[2]通过在Bladed中开发地震模块，研究了地震对塔基极限载荷的影响，并与频域法进行比较。Santangelo等[3]基于Bladed研究了风-震耦合效应对5 MW风力机塔基载荷和塔顶位移等动态响应的影响。Asareh等[4-5]基于大质量法在开源软件FAST中开发了地震动力学分析模块Seismic，研究了地震强度对风力机发电功率和塔架载荷的影响[6]。Yang等[7-8]通过Wolf模型定义土壤刚度和阻尼，研究了不同强度地震与湍流风耦合效应对5 MW风力机塔顶振动和塔基载荷的影响，并提出了一种地震条件下塔架极限载荷的预估模型。

以上研究对象均为陆上风力机，而海上风力机支撑结构更长，地震对塔顶振动的影响更大。为此，闫阳天等[9]采用Ansys软件研究了风-震弱耦合条件下桁架式风力机地震动态响应特性。Mo等[10]在OpenSees中建立了5 MW海上风力机风-震弱耦合模型，首先通过FAST计算风力机气动载荷，再将气动力输入至OpenSees中分析塔架结构动态响应特性。Yang 等[11-12]研究了土-构耦合(Soil Structure Interaction, SSI)效应对5 MW单桩风力机地震动态响应的影响。

由于以上文献主要针对5 MW风力机，在降低度电成本要求下，15 MW风力机将逐步增加，在地震发生时大型风力机的SSI效应更为明显。因此，有必要研究SSI效应对下一代超大型海上风力机地震动态响应的影响。为此，笔者基于模态加速度方法在FAST中建立风力机地震载荷计算模型，采用耦合弹簧模型表征支撑结构与海床的SSI效应，通过比较考虑及忽略SSI效应时，15 MW风力机在运行及停机状态下的地震诱导振动和结构载荷特性，研究SSI效应对地震动态响应的影响，以期为下一代超大型海上风力机结构抗震设计提供参考。

1 风力机及土-构耦合模型

1.1 风力机模型

为满足下一代大型风力机的研究需求，美国可再生能源实验室(National Renewable Energy Laboratory，NREL)与丹麦科技大学(Technical University of Denmark，DTU)在国际能源署(International Energy Agency,IEA)的资助下，于2020年合作设计了一台专用于海上风电研究的15 MW直驱型样机[13]，其主要尺寸见图1。

图1 单桩基础的15 MW风力机示意图Fig.1 Diagram of 15 MW monopile wind turbine

该风力机直径达240 m，轮毂高度为150 m，是目前公开用于学术研究的尺寸最大的风力机。其额定风速和转速分别为10.59 m/s和7.56 r/min，对应的尖速比为9，最大叶尖速度为95 m/s。叶片长度为117 m，质量达64 t，塔顶总质量约为1 017 t。该单桩直径为10 m，应用水深为30 m，泥面下长度为45 m，总质量约1 318 t。

1.2 土-构耦合模型

由于地震发生时，土壤柔性特征更为明显，刚性基础假设存在一定误差。为获取更准确的风力机地震动态响应特性，通过耦合弹簧模型表示土壤与结构的相互作用，如图2所示。图中K和C分别表示刚度和阻尼，下标“t”表示平动方向，“r”表示转动方向。平动和转动方向均存在3个线性弹簧，表征土壤反应力。

假设土壤为典型硬土，其剪切模量(Gs)和泊松比(νs)分别为140 MPa和0.4。各方向的SSI模型弹簧刚度[14]可表示为：

(1)

(2)

(3)

(4)

(5)

(6)

式中：Kx、Ky和Kz分别为纵向、横向和垂向刚度；Krx、Kry和Krz分别为绕x轴(面内)、y轴(面外)和z轴(扭转)土壤刚度；h和r0分别为单桩泥面下长度和半径，其值分别为45 m和5 m；ηx和ηφ分别为水平方向和扭转方向的刚度修正系数。

图2 土-构耦合模型Fig.2 Soil-structure interaction model

1.3 支撑结构模态

考虑SSI效应时，桩基底部为弹性边界条件，将极大地影响支撑结构(塔架+单桩)的模态特性。图3比较了所研究风力机支撑结构的模态振型，对应的固有频率见表1。

从图3可以看出，SSI效应对支撑结构二阶模态振型具有明显影响，与忽略SSI效应相比，其二阶前后模态最大位移从4.78增大至9.62，二阶侧向模态最大位移从3.11增大至6.29。由于地震激励高频段能量较大，易诱发结构发生高阶模态振动。可预见的是，考虑SSI效应时，地震诱导结构振动将显著增大。

从表1可以看出，与忽略SSI效应相比，考虑SSI效应时，支撑结构一阶和二阶频率均有所降低，说明SSI效应对系统振动有显著影响。需要注意的是，该15 MW风力机额定转速和最低转速分别为7.56 r/min和5.0 r/min，对应的旋转频率区间和叶片通过频率区间分别为0.524～0.760 Hz和1.571～2.278 Hz，与塔架频率无重叠，说明诱发共振的概率较低。

2 地震载荷计算模型

通过对风电仿真开源软件FAST进行二次开发，修改结构动力学计算相关源代码，采用模态加速度法计算地震载荷，实现地震载荷与风、浪、流载荷及结构弹性的耦合。

图3 支撑结构的模态振型Fig.3 Mode shapes of the support structure

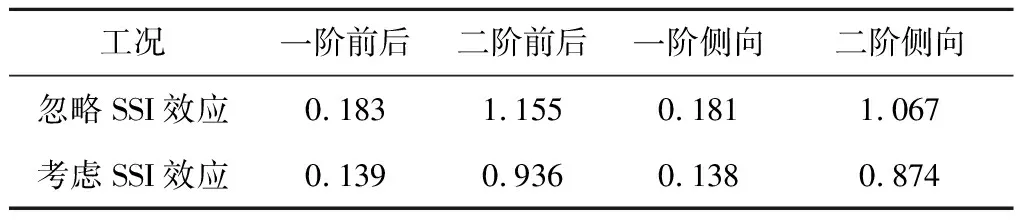
表1 支撑结构模态固有频率

2.1 FAST动力学模型

FAST是由NREL开发的专用于水平轴风力机气动-水动-伺服-弹性多场耦合仿真的知名开源软件。在FAST中，风力机被视为由柔体和刚体组成的多体系统，通过线性假设模态法求解叶片和塔架等柔体的弹性变形，采用Kane方法建立系统动力学方程，如式(7)所示。

(7)

(8)

式中：H为塔架高度；ρTwr(h)和aTwr(h)分别为塔架质量密度和加速度；vi,Twr(h)为第i个自由度对应的偏速度。

广义主动力则主要包括气动力Fi,a、弹性力Fi,e、重力Fi,g和阻尼力Fi,d以及地震载荷Fi,eq，如式(9)所示。

Fi=Fi,a+Fi,e+Fi,g+Fi,d+Fi,eq

(9)

将不同模块计算得到的主动力代入式(7)中，即可求解风力机各个自由度对应的惯性加速度，从而获取各结构部件的运动参数和载荷等动态响应。

2.2 地震载荷计算

大质量法是目前较为常见的一种地震载荷计算方法，该方法假定塔架底部存在一大质量弹簧振子，在地震发生时会剧烈振动并产生相应载荷，通过给定其质量、振动频率和阻尼即可计算相应地面振动下的地震载荷。由于该方法原理简单且易于实现，因此Asareh等基于该方法开发了风力机地震仿真程序NREL Seismic[6]。但需要注意的是，该方法需要人工指定弹簧振子质量和振动频率，对于不同的风力机模型，可能存在较大计算误差，且难以计及SSI效应对振动频率的影响。对于柔性土壤边界条件，需要进行一定的改进和修正。为此，通过结构模态质量和地震加速度计算塔架受到的地震载荷。该方法的优势在于，地震载荷计算过程中没有经验参数，且可以通过结构模态的变化考虑土-构耦合效应。作用于塔架的地震载荷为：

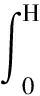
(10)

式中：Fi,eq为塔架第i阶模态的地震载荷；φi(h)为归一化模态振型；aeq为地震加速度。

质量为mtop的塔顶结构受到的地震载荷Feq,top为：

Feq,top=aeq·mtop

(11)

由于未考虑轴向模态，垂向地震加速度aeq,ver对风力机造成的地震载荷Feq,ver为：

Feq,ver=aeq,ver·mturbine

(12)

式中：mturbine为风力机总质量。

将式(10)～式(12)计算得到的地震载荷与风、浪载荷相结合，代入式(9)中求解风力机主动力，以考虑风、浪与地震的耦合效应。图4为本文所提出的风力机地震动力学分析系统中各模块耦合逻辑图。

图4 风力机地震动力学分析流程图

3 环境载荷

3.1 湍流风场及波浪

本文拟研究地震激励对海上风力机结构动力学特性的影响，为保证结果的可靠性及准确性，需考虑风、浪及地震等多载荷的联合作用。针对湍流风，采用TurbSim生成平均风速为10.59 m/s、时长为1 000 s的全流域湍流风场，风场尺寸为300 m×295 m，以轮毂为中心，可覆盖整个塔架及风轮。图5为不同时刻风轮平面及轮毂高度处风速分布。

通过JONSWAP波浪谱定义非规则波浪频率分布，根据文献[15]给出的美国西海岸实测风速和波浪数据，风速为10.59 m/s时，有义波高和谱峰周期分别为5.2 m和12.5 s，基于Airy线性波浪理论生成波浪高度、速度和加速度等，通过Morison方程计算单桩水动力载荷。

3.2 地震激励

为研究SSI效应对地震条件下15 MW风力机极限载荷的影响，选择如表2所示的5种发生于不同地区的地震。其中，由P.D.d基站监测的发生于1994年的美国加州Northridge地震地面加速度峰值为0.552g。该地震加速度包含水平(x、y)和垂直(z)3个方向的地震波，地震加速度如图6所示，持续时长约40 s。

4 结果与分析

采用所建立的风力机地震动力学仿真模型，分别计算考虑及忽略SSI效应时15 MW风力机在正常运行工况和停机状态下的支撑结构加速度和载荷等响应参数，以探究SSI效应对地震条件下风力机振动及载荷的影响。每个算例的仿真时长为680 s，时间步长为0.002 s。为降低风力机启动时瞬态效应的影响，地震载荷在第600 s时加入。为使结果表达简洁且不失一般性，仅给出了Northridge地震作用下的时域响应。

(a) 风轮平面

(b) 轮毂高度处图5 不同时刻风轮平面及轮毂高度处风速分布

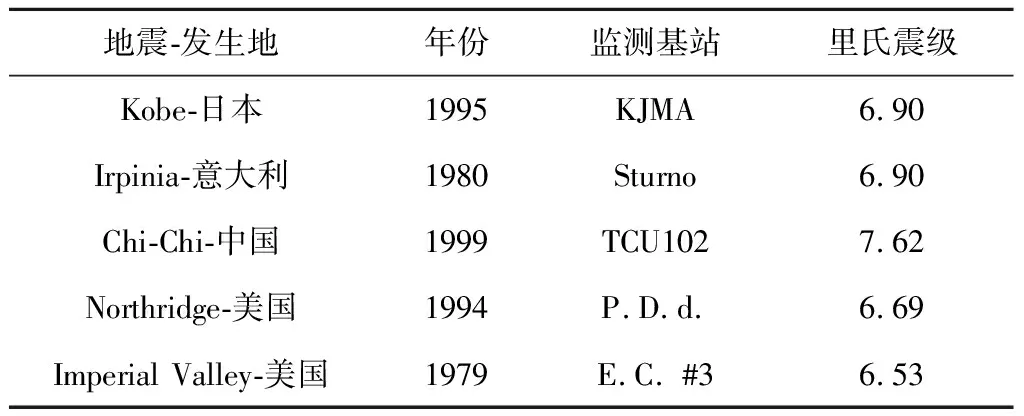
表2 地震实测记录

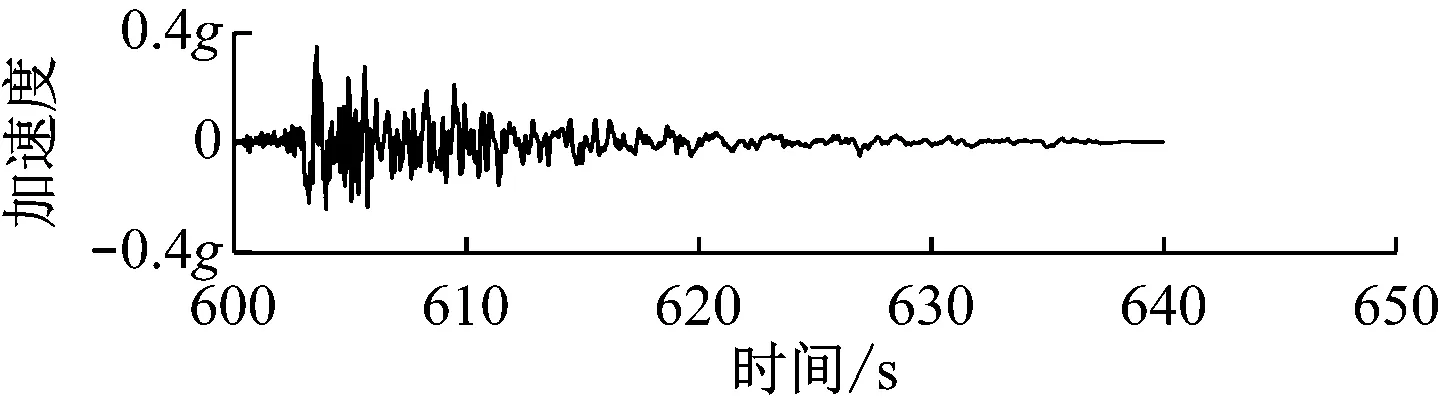
(a) Northridge-x

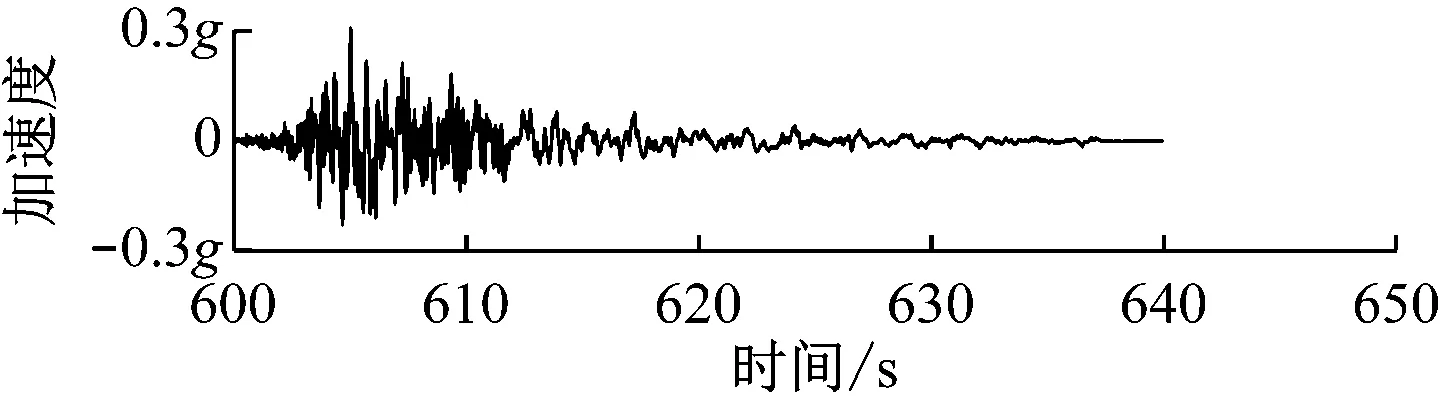
(b) Northridge-y

(c) Northridge-z图6 Northridge地震加速度时域变化Fig.6 Ground motions of the Northridge earthquake event

4.1 塔顶振动特性

在地震作用下，风力机将发生剧烈振动。为研究SSI效应对15 MW风力机地震诱导振动的影响，图7比较了考虑及忽略SSI效应2种情况下风力机在正常运行时的塔顶加速度。

(a) 前后加速度

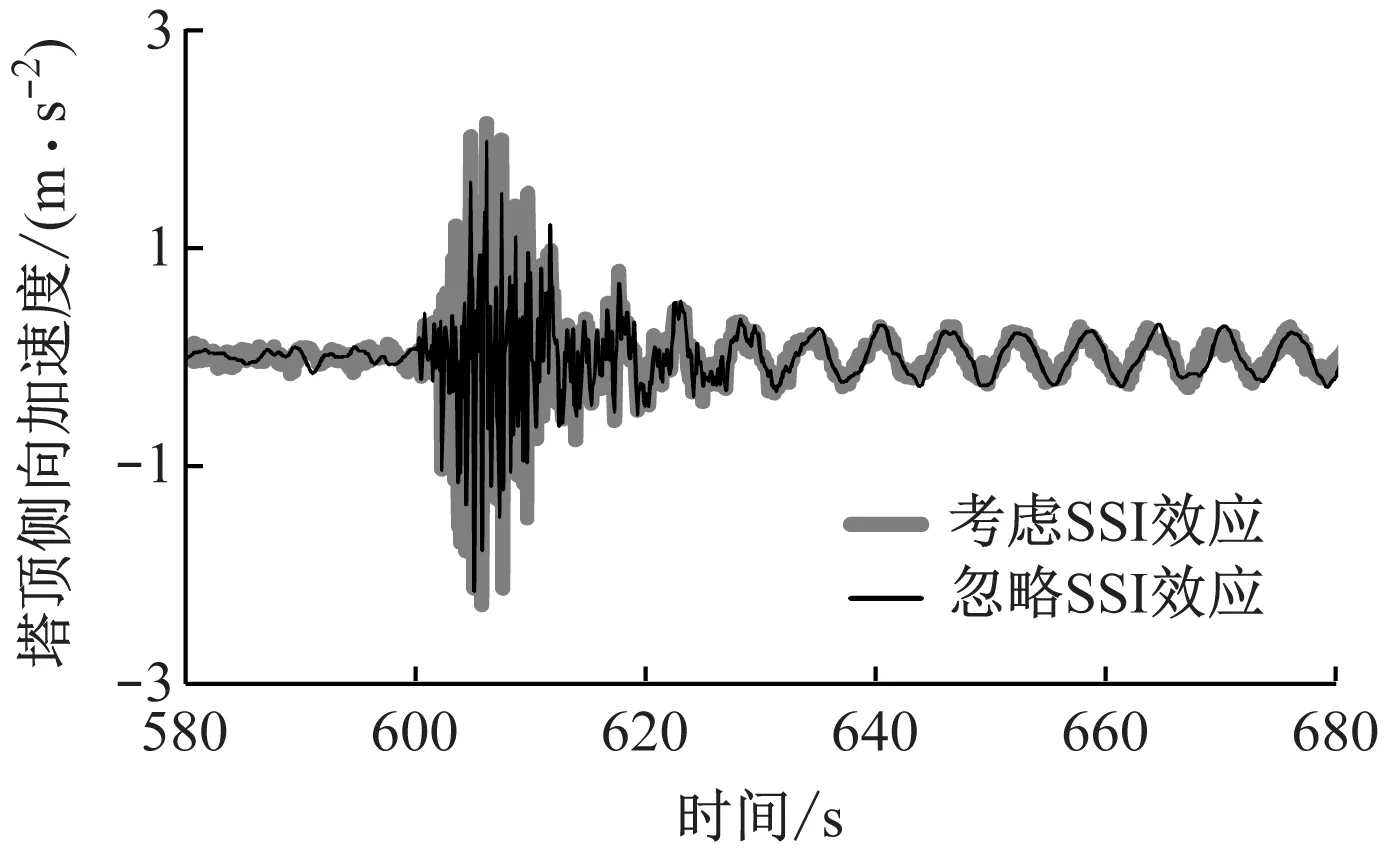
(b) 侧向加速度图7 正常运行工况下塔顶加速度的变化

从图7可以看出，在地震发生前，塔顶前后方向加速度在风载荷作用下在-0.32～0.16 m/s2内波动，侧向气动载荷变化较小，塔顶振动较微弱。600 s时发生地震后，考虑及忽略SSI效应2种情况下，塔顶前后加速度均急剧增大，峰值分别为3.63 m/s2和3.90 m/s2。

图8给出了停机状态下考虑及忽略SSI效应时塔顶加速度的变化情况，此时发电机关闭且叶片处于顺桨状态。由图8可以发现，考虑及忽略SSI效应2种情况下塔顶前后及侧向加速度峰值差别较小，说明SSI效应对停机状态地震诱导塔顶振动剧烈程度的影响较小。但需要注意的是，在640 s地震结束后，考虑SSI效应时的塔顶侧向加速度波动明显更大，前后方向却未发生类似情况。620～680 s内，考虑及忽略SSI效应时塔顶侧向加速度标准差分别为0.44 m/s2和0.08 m/s2。这主要是因为忽略SSI效应时，塔顶振动在自身结构阻尼的作用下逐渐减小。而考虑SSI效应时，结构振动能量被土壤吸收，而下一循环又释放给支撑结构，极大地削弱了结构自身阻尼的耗散作用。而在前后方向，由于存在一定的气动阻尼，可以用于耗散地震激励能量。由图8(a)还可以看出，尽管考虑SSI效应时，在620 s后塔顶前后方向振动加速度略微大于忽略SSI效应时，但整体降低的趋势较为明显。这一结果说明，SSI效应对停机状态下地震诱导塔顶振动具有较为显著的影响。

(a) 前后加速度

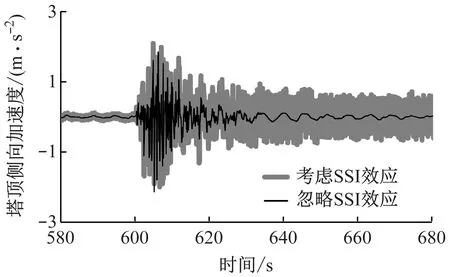
(b) 侧向加速度图8 停机状态下塔顶加速度的变化Fig.8 Tower top acceleration variation under the parked condition

4.2 支撑结构泥面载荷

地震发生时，必将导致支撑结构承受载荷剧烈增加，特别是泥面处支撑结构弯矩。图9为正常运行工况下考虑及忽略SSI效应时泥面处支撑结构弯矩变化。从图9可以看出，地震发生后支撑结构泥面处面内弯矩急剧增大。考虑SSI效应时，支撑结构弯矩增大更为明显。由于正常工况下风力机气动载荷较大，地震对忽略SSI效应时的面外弯矩影响较小，但考虑SSI效应时面外弯矩显著增大。考虑和忽略SSI效应时泥面处弯矩最大值分别为777.2 MN·m和540.0 MN·m。这一结果说明，忽略SSI效应会导致地震极限弯矩预估值偏低29.6%。

图10给出了停机状态下考虑及忽略SSI效应时泥面处支撑结构弯矩变化。从图10可以看出，SSI效应对停机状态地震极限载荷的影响更大。考虑SSI效应时，泥面处最大弯矩为463.3 MN·m，而忽略SSI效应时为259.2 MN·m。

此外，需要特别注意的是，忽略SSI效应时，面内弯矩在地震结束后逐渐减小；而考虑SSI效应时，支撑结构弯矩下降速率明显更低，说明此时结构自身阻尼无法消耗地震激励能量。结构运动产生的作用力被海床吸收并储存，在结构运动至极限状态(即变形/位移值最大)时，转换成对结构的反作用力，使得结构面内弯矩变化幅度一直处于较高水平。

(a) 泥面处面内弯矩

(b) 泥面处面外弯矩图9 正常运行时支撑结构泥面弯矩

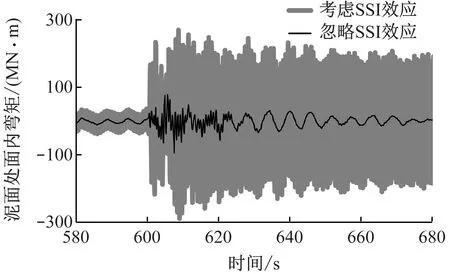
(a) 泥面处面内弯矩

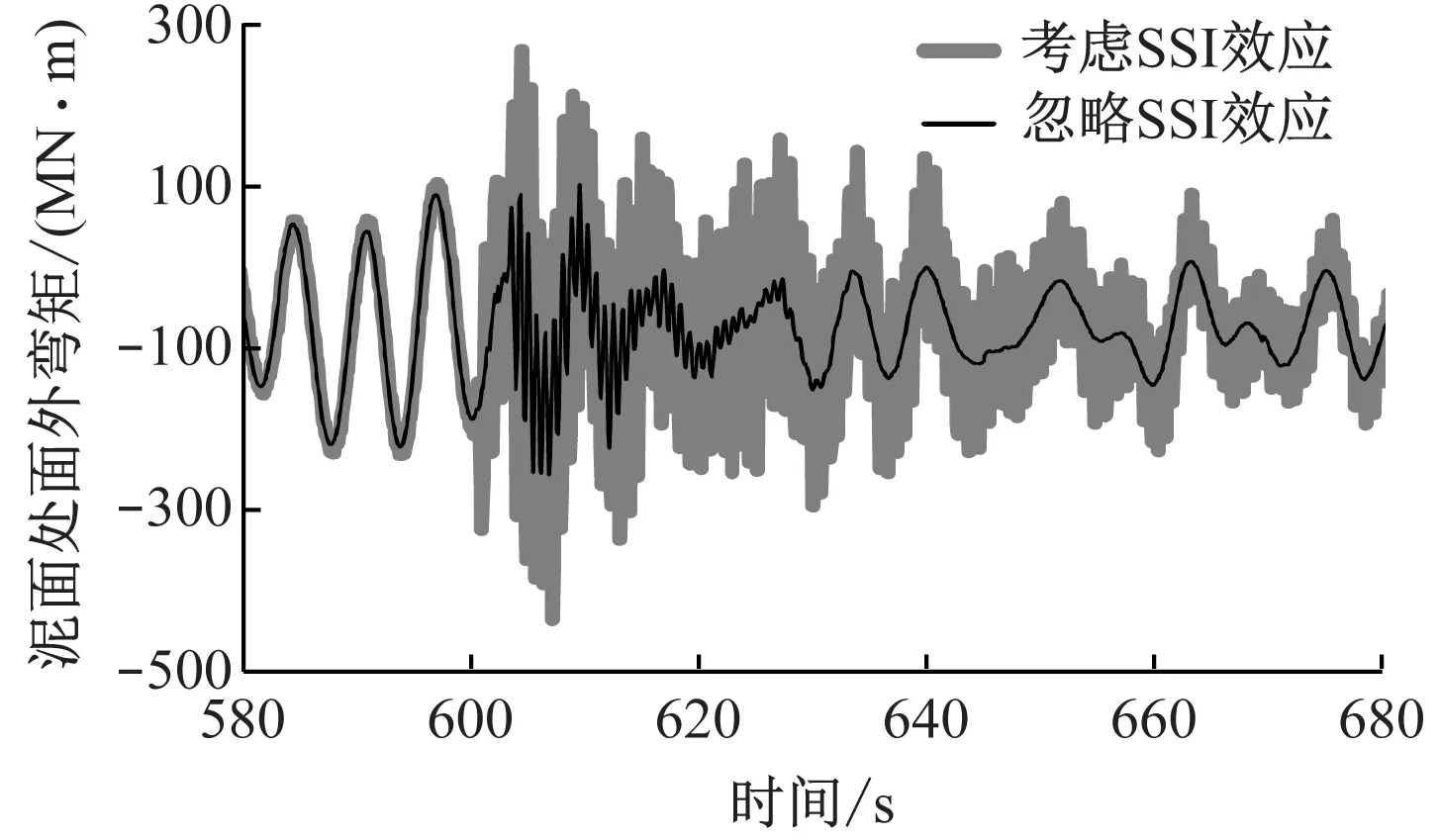
(b) 泥面处面外弯矩图10 停机状态下支撑结构泥面弯矩

相反地，在面外方向，由于存在湍流风与风轮的相互作用，一定程度上增加了气动阻尼，可以耗散地震激励能量。尽管考虑SSI效应时的面外弯矩变化幅值大于忽略SSI效应时，但地震结束后其幅值有明显下降趋势，并在680 s左右与忽略SSI效应时的幅值保持在同一水平。这一结果说明忽略SSI效应会极大地低估地震载荷对支撑结构极限载荷及疲劳载荷的影响。同时也说明，在地震发生后，应该及时增加阻尼系统，以降低结构面内弯矩变化幅值。

4.3 支撑结构泥面极限载荷

为进一步说明SSI效应对地震条件下支撑结构载荷的影响，图11给出了5种地震作用下，考虑及忽略SSI效应时泥面处支撑结构的最大剪切力和弯矩。

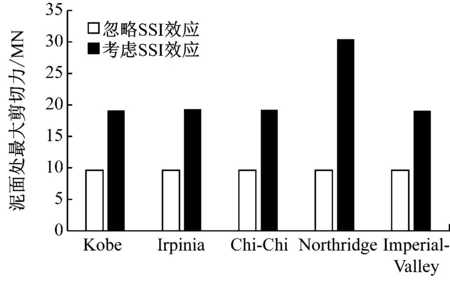
(a) 泥面处最大剪切力

(b) 泥面处最大弯矩图11 不同地震工况下泥面处最大剪切力和弯矩

从图11可以看出，忽略SSI效应时，不同地震工况下泥面处支撑结构最大剪切力和弯矩均较为接近，而考虑SSI效应时，不同工况之间的差距变大。忽略SSI效应导致最大剪切力和弯矩的计算结果均偏低。其中，Northridge地震工况下，忽略和考虑SSI效应时的最大剪切力分别为9.68 MN和30.27 MN，忽略SSI效应导致剪切力偏低达到68.0%，在5种地震工况下偏低程度最高。同样，弯矩偏差也达到29.6%。这一结果再次说明风力机结构抗震设计中考虑SSI效应的必要性。

5 结 论

(1) SSI效应对地震诱导振动剧烈程度影响较弱，但对停机状态下塔顶侧向振动耗散的速度具有一定影响。

(2) 泥面处支撑结构弯矩受到SSI效应的影响较大，忽略SSI效应时将导致泥面处弯矩最大值预估结果偏低约29.6%。

(3) 忽略SSI效应时，面内弯矩计算值偏低，将会低估地震激励的影响，特别是会低估地震结束后的结构疲劳载荷。

(4) 在设计地震多发区域的海上风力机结构时，应考虑增加阻尼系统，以及时降低地震发生后的面内弯矩幅值。