变热源有机朗肯循环系统的综合性能分析
李慧君, 蒋长辉, 范 伟, 王庆五
(华北电力大学 能源动力与机械工程学院,河北保定 071003)
中低温余热发电技术的应用潜力巨大,在工业余热和新型能源的开发利用中具有广阔的应用前景[1]。由于结构简单、安全可靠、热效率高等优势,有机朗肯循环(ORC)余热发电技术引起了国内外学者的广泛关注,并针对其开展了大量研究[2]。
Invernizzi等[3]通过仿真模拟,发现R1234ze和R1234yf的净功率不及R134a。Wang等[4]选用R1233zd和R1234yf作为工质,发现系统效率得到显著提升。杨见森等[5]以某化工厂温度为105 ℃的排空蒸汽余热为热源,以R134a为系统循环工质,提出了有机朗肯循环的简化模型,并基于此分析了系统热效率和效率。韩中合等[6]以热效率和单位输出功率的系统总投资成本(PER)作为优化目标,引入多目标蜻蜓算法(MODA算法)进行多目标优化,发现在帕累托前沿中,随着热效率的增加,变透平效率下PER迅速增加,而定透平效率下PER的增速相对较平缓。Zhang等[7]以电力生产成本和成本回收期为优化目标,经过参数优化发现随着工质临界温度的升高,蒸发器中的最佳夹点温差具有减小的趋势,而冷凝器中的最佳夹点温差几乎保持不变。韩中合等[8]以平板式换热器为蒸发器,选择板长、板宽和平板间距为优化变量,基于非支配遗传算法进行多目标优化,发现R245ca的综合性能最优,R245fa和R123的综合性能次之。郭贵奇等[9]以效率和比投资成本为优化目标,建立了结构参数和运行参数同步优化的多目标优化模型,利用遗传算法进行多目标优化,获得了最佳运行参数和换热器结构参数。Bu等[10]通过计算各组元的单位产品成本、单位热经济学成本和发电成本,实现了热力系统经济性能与能效水平的联合评价。
综上所述,研究者一般以多参数为控制变量建立针对某一个或多个系统性能指标的优化模型进行系统参数寻优或性能优化。但这些研究针对的系统性能是以热力性能(热效率、净输出功等)为指标的,部分学者考虑辅以经济性能(电力生产成本、单位质量净输出功等),只有极少部分学者是以系统的综合性能为指标,且多数是在定热源参数下进行的。
1 数学物理模型
1.1 热力学模型
有机朗肯循环系统的主要部件有蒸发器、透平(膨胀机)、冷凝器和工质泵。ORC系统构成和换热器中换热流体的温度变化如图1所示。

图1 ORC系统简图Fig.1 Schematic diagram of the ORC system
工质在蒸发器中的吸热量Qeva为:
Qeva=qm,f(h3-h1)=qm,gcp,g(Ths-Tout)
(1)
式中:qm,f为工质质量流量,kg/s;hi为图1中状态点i处的焓,kJ/kg,i=1~6;qm,g为热源质量流量,kg/s;cp,g为热源的比定压热容,kJ/(kg·K);Ths、Tout分别为热源的进、出口温度,K。
工质在冷凝器中的放热量Qcon为:
Qcon=qm,f(h4-h6)
(2)
工质在透平中的做功量Wtur为:
Wtur=qm,f(h3-h4)
(3)
产生的工质泵功Wpump为:
Wpump=qm,f(h1-h6)
(4)
循环净输出功Wnet为:
Wnet=Wtur-Wpump
(5)
Eex,i=qm,f[(hi-h0)-T0(si-s0)]
(6)
式中:Eex,i为状态点i处的,kW;si为状态点i处的熵,kJ/(kg·K);h0、s0分别为工质在环境温度下的焓和熵, kJ/kg,kJ/(kg·K);T0为环境温度,K。
Itur=Eex,3-Eex,4-Wtur
(7)
Ipump=Eex,6-Eex,1+Wpump
(8)
Ieva=T0Qeva[(Tlogex-Ten)/Tlogex]/Ten
(9)
Icon=T0Qcon[(Tex-T0)/T0]/Tex
(10)
式中:Itur、Ipump、Ieva、Icon分别为透平、工质泵、蒸发器和冷凝器的损,kW;Ten为循环平均吸热温度,K;Tex为循环平均放热温度,K;Tlogex为热源对数平均放热温度,K。
ηex=1-I/Eex
(11)
式中:I为系统总损,kW;Eex为热源向系统提供的代价,kW。
1.2 经济模型
系统设备总成本C1996(按1996年设备结构价格)计算式[11]为:
C1996=CBM,E+CBM,T+CBM,C+CBM,P
(12)
式中:CBM,E、CBM,C、CBM,T、CBM,P分别为蒸发器成本、冷凝器成本、透平成本和水泵成本,美元。
系统设备总成本Ctot为:
Ctot=C1996CCEPCI,2019/CCEPCI,1996
(13)
式中:CCEPCI为化工成本指数,根据文献[11]和文献[12],1996年的化工成本指数CCEPCI,1996取382,2019年的化工成本指数CCEPCI,2019取607.5。
各设备成本CBM为:
CBM=Cb(B1+B2FMFP)
(14)
式中:B1、B2为设备相关系数;FM为设备材料因子;FP为设备压力因子;Cb为基准成本,美元。
lgFP=C1+C2lgp+C3lg(10-5p)2
(15)
式中:p为各设备在设计参数下的承压,Pa;C1、C2、C3为各设备压力因子计算系数。
基准成本Cb计算式[11]为:
lgCb=K1+K2lgM+K3(lgM)2
(16)
式中:K1、K2、K3为设备成本计算系数;对于换热器,M为换热面积,m2;对于透平,M为做功量,kW;对于工质泵,M为泵功,kW。
净现值是指收益折现后与投资额的差值,被认为是评估系统经济性能的最佳单一指标[13]。净现值CNPV[14]为:
CNPV=-Ctot+
(17)
售电所得收益Cinc为:
Cinc=WnetτopCoe
(18)
式中:ay为设备寿命,a;rtax为税率,%;τop为系统年运行小时数,h;Coe为电价,美元/(kW·h);r为年利率,%;Dep为系统资产年折旧,美元;Com为系统运行维护成本,美元。
2 多目标优化模型
笔者选择HFOs类环保工质R1234ze、湿工质R134a和干工质R245fa为系统工质,三者的主要参数见表1。
选择蒸发温度Teva、热源进口温度Ths和窄点温差Δt为优化变量,效率和净现值为目标函数。通过权重系数,构建效率和净现值的综合目标函数Fx为:
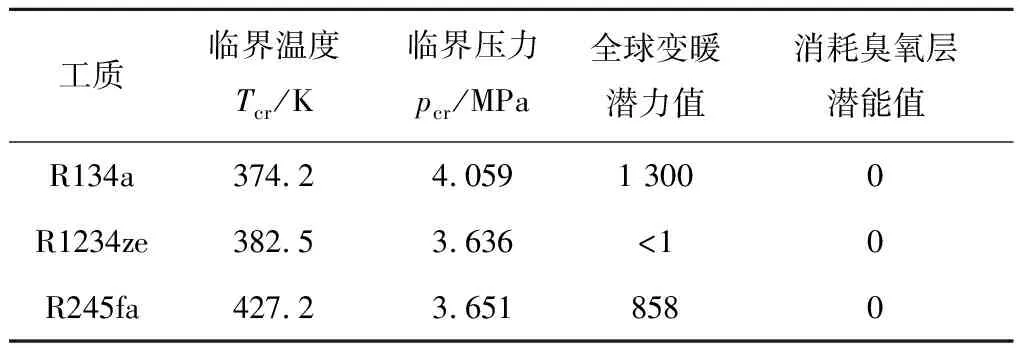
表1 有机工质的主要参数
Fx=af1(x)+bf2(x)
(19)
式中:a、b为权重系数;f1(x)为净现值的目标函数;f2(x)为效率的目标函数。由于净现值与效率的数值差距过大,现将效率值乘上系数5×106,系数只会影响权重系数的值,不会影响系统运行参数的择优结果。
(22)
初始条件如下:环境温度为25 ℃,冷凝温度为30 ℃,过热度为10 K。热源采用导热油DY300,导热油质量流量取10 kg/s。透平的等熵效率为0.8,泵的等熵效率为0.75,发电机效率为1。年运行发电时间为7 500 h ,银行年利率取0.045,设备寿命20 a,系统运行维护成本取设备总成本的1.5%,税率取15%,净残值率取5%,电价为0.15美元/(kW·h)[13]。
3 建立综合目标函数
3.1 α法确定权重系数
采用α法求解a、b:
(23)
(24)
式中:f11为f1(x)的最大值;f12为f1(x)取最大值时所对应的f2(x)的值;f22为f2(x)的最大值;f21为f2(x)取最大值时所对应的f1(x)的值。
3.2 基于帕累托解集确定权重系数
以R245fa为例,其系统帕累托最优边界曲线如图2所示。R245fa对应的系统效率最大的点为E点,在该点的热力性能最优,经济性能最差;而N点的经济性能最优(净现值最大),热力性能最差。同时具有最大效率和净现值的点是不存在的。采用工程决策法,做一个理想辅助点I,距离该点最近的点被认为是帕累托最优解。
若将帕累托解集带入式(19),帕累托最优解对应的Fx值应该是最大的。因此,可根据帕累托最优解确定权重系数。
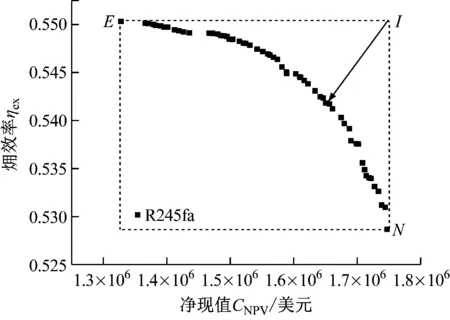
图2 R245fa对应的帕累托最优边界Fig.2 Pareto optimal boundary corresponding to R245fa
4 系统综合性能分析
4.1 2种确定权重系数方法比较
采用α法确定权重系数,建立综合目标函数Fx,并分别以效率、净现值和Fx为目标函数,采用遗传算法对系统进行单目标优化,结果见表2。其中p3为状态点3的压力,t4为状态点4的温度。

表2 遗传算法优化结果
从表2可以看出,在所选工质中R1234ze的净现值最大,即具有最优的经济性能,其效率略低于R134a。与R245fa相比,R1234ze的净现值和效率分别提高了约20.11%和9.66%;与R134a相比,R1234ze的净现值提高了约12.57%,效率降低了约0.03%。R134a具有最优的热力性能。
以R1234ze为例,以Fx为目标函数进行优化时,较效率为优化目标时的效率降低了约2.5%,但净现值提高了约0.9%;较净现值为优化目标时的净现值减小了约0.5%,但效率提高了约2.3%。综上所述,Fx能同时兼顾系统的热力性能和经济性能。
采用带精英策略的非支配排序的遗传算法(NSGA-II算法)对ORC系统进行双目标优化,结果如表3所示。
从表3可以看出,帕累托最优解同样可以兼顾系统的热力性能与经济性能。以R1234ze为例,相比于以Fx为优化目标,以效率为优化目标时,效率提高了约2.55%,净现值减小了约0.92%;以净现值为优化目标时,净现值提高了约0.46%,效率降低了约2.23%。但是,帕累托最优解并不能反映热力性能与经济性能的权重,也不能以此分析运行参数对系统综合性能的影响。
对比表2和表3可知,通过α法和帕累托解集确定的权重系数有差异,但是各工质热力性能与经济性能的偏重性一致。各工质优化的效率、净现值和Fx所对应的系统运行参数相似,误差不大。这可能是由于算法参数的取值(如迭代次数、交叉变异因子、最优个体系数等)不是唯一的,造成了上述差异。
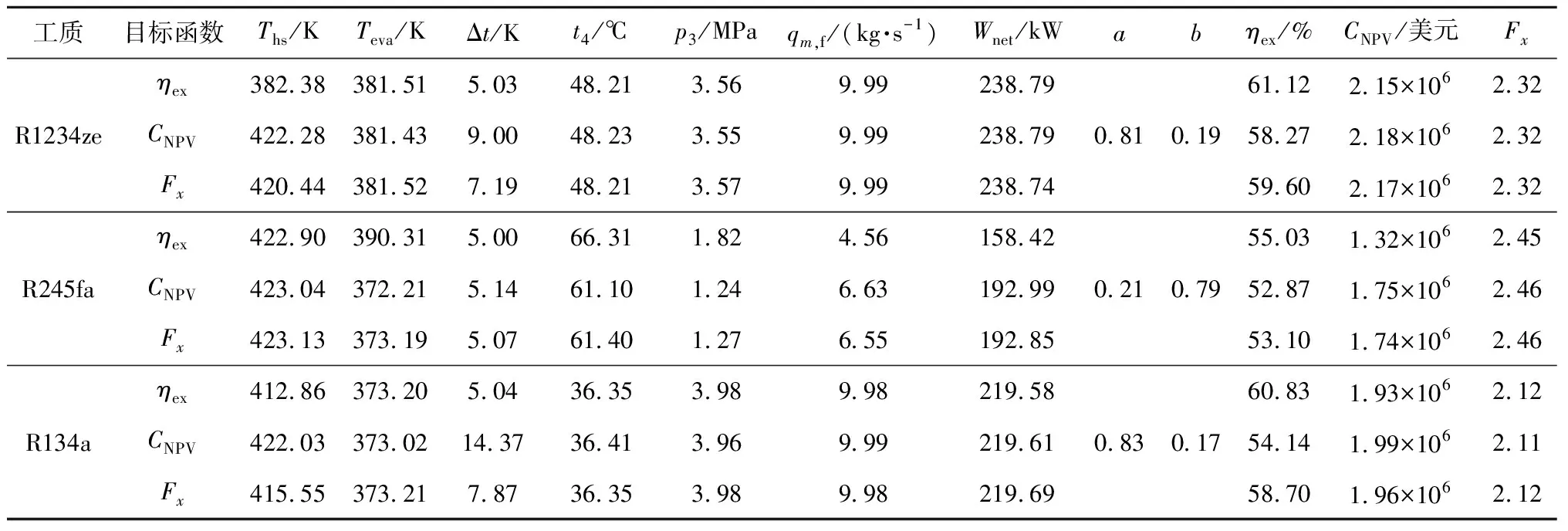
表3 NSGA-II算法优化结果
4.2 优化变量对系统综合性能的影响
由于R245fa偏重于热力性能,因此本节综合R1234ze和R134a 2种工质,根据式(19)建立统一的综合目标函数:
Fx=[0.82f1(x)+0.18f2(x)]/106
(25)
相较常规遗传算法,NSGA-Ⅱ算法以密度值估计策略和快速非支配排序策略确保了算法的收敛效率。其中a、b取值0.82和0.18为表3中R1234ze和R134a 2种工质取得的权重系数的平均值。
窄点温差为7 K和15 K,热源进口温度分别为403 K、408 K和413 K时,系统Fx随蒸发温度的变化趋势如图3所示。由图3(a)可知,窄点温差为7 K时,随着热源进口温度从403 K升高到413 K,R1234ze对应的系统Fx值随蒸发温度的升高由先增后减变为只增不减;而R134a对应的系统Fx值随蒸发温度的升高不断增大。由图3(b)可知,窄点温差为15 K时,R1234ze对应的系统Fx值随蒸发温度的升高先增大后减小;R134a对应的系统Fx值随蒸发温度的升高由先增后减变为只增不减。这是由于蒸发温度变化会同时影响系统的效率和净现值:蒸发温度升高,会使热源与蒸发器间的换热温差减小,从而使系统损减小,效率提高;同样也会使透平进口比焓增加,工质质量流量减小,二者的变化速率先后占据优势,从而使系统净现值先增后减。

(a) Δt=7 K

(b) Δt=15 K图3 综合目标函数随蒸发温度的变化Fig.3 Variation of comprehensive objective function with evaporation temperature
热源进口温度升高,系统的Fx值增大。在热源进口温度升高的过程中,蒸发温度升高对工质质量流量减小的影响越来越小,使系统净现值只增不减,Fx值只增不减。窄点温差增大使系统的Fx值减小。在窄点温差增大的过程中,蒸发温度升高对工质质量流量减小的影响越来越大,使系统净现值先增后减出现最值。
计算结果表明,窄点温差为7 K,热源进口温度为403 K和408 K时,R1234ze的最优系统Fx值对应的最优蒸发温度分别约为356 K和361 K。窄点温差为15 K,热源进口温度为403 K、408 K和413 K时,R1234ze的最优系统Fx值对应的最优蒸发温度分别约为350 K、354 K和358 K;热源进口温度为403 K和408 K时,R134a的最优系统Fx值对应的最优蒸发温度分别约为351 K和356 K。
随着热源进口温度的升高,各工质最优系统综合目标函数值对应的最优蒸发温度升高;而随着窄点温差升高,各工质最优系统综合目标函数值对应的最优蒸发温度降低。综合图3(a)、图3(b)发现,当蒸发温度低于361 K时,R1234ze的系统Fx值大于R134a的系统Fx值;蒸发温度高于361 K时,R134a的系统Fx值大于R1234ze的系统Fx值。
控制窄点温差和蒸发温度不变,综合目标函数随热源进口温度的变化趋势如图4所示。热源进口温度升高,Fx值增大;窄点温差升高,Fx值减小。对比图4(a)和图4 (b)发现,蒸发温度在363 K左右时,R134a对应的系统Fx值与R123ze相似;蒸发温度在373 K左右时,R134a对应的系统Fx值要大于R1234ze的系统Fx值。
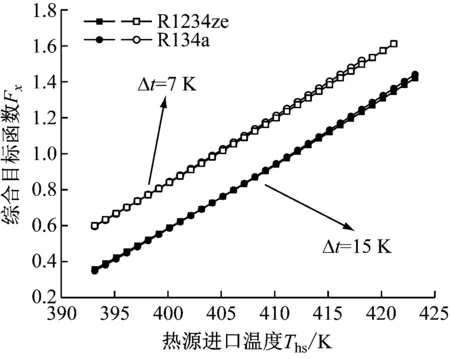
(a) Teva=363 K

(b) Teva=373 K图4 综合目标函数随热源进口温度的变化Fig.4 Variation of the comprehensive objective function with the inlet temperature of the heat source
5 结 论
(1) 所构建的综合目标函数Fx可同时反映系统的热力性能和经济性能,更能满足工程实际要求。
(2) 以Fx为目标函数进行优化时,R1234ze的效率和净现值均好于R245fa和R134a,其应用潜力巨大。
(3) 综合经济性分析下,根据工质的临界温度合理选择热源参数,可得到一个最优的蒸发温度使综合目标函数Fx取到最大值,且蒸发温度最优值随热源进口温度的升高而增大,随窄点温差的升高而减小。
(4) 综合经济性分析下,当蒸发温度在361 K左右时,R1234ze和R134a的系统综合性能大小关系发生转变。蒸发温度低于361 K时,R1234ze的系统综合性能优于R134a。
(5)α法和帕累托解集确定的权重系数有差异,但是各工质热力性能与经济性能的偏重性一致,且各工质最优效率、净现值和Fx对应的系统运行参数相似,误差不大。

