沿海资源富集区景观格局脆弱度的时空演变特征分析

李辉辉，杨永崇，杜 嵩，杨梅焕，陈宝强

(西安科技大学测绘科学与技术学院，陕西 西安 710054)

景观格局指数是反映景观结构组分、空间配置特征的量化指标，具有高度浓缩的景观格局信息[1-3]。景观格局变化与生态过程紧密相关，通过景观格局指数构建景观格局脆弱度评价指标体系，进而研究生态环境具有重要的意义[4-6]。景观格局脆弱度是指景观格局受到自然或人为因素影响时，所表现出的景观生态敏感性和缺乏适应能力，从而导致景观系统结构、功能和特性易发生改变的属性[7-8]。景观格局脆弱度分析通过剖析景观格局信息与景观格局生态脆弱性之间的关联性，建立具有生态学意义的评价指标体系，从而为区域生态环境脆弱性评价提供新的思路和方法[9]。目前，国内外学者对景观格局脆弱度的研究多集中在土地利用/覆盖对景观格局脆弱度的空间分布特征及时空变化分析[10-11]，有学者[12]通过增加海拔和坡度两种影响因素重新构建景观敏感性，分析了景观格局脆弱度变化。景观格局受外界扰动后，其结构、功能和特性容易发生改变，郭少壮等[13]通过构建人为干扰度模型，分析了秦岭地区景观格局脆弱度与人为干扰度之间的关系；孙鸿超等[14]运用随机森林建模探究了景观格局脆弱度变化的驱动因素。就影响因素而言，当前对景观格局脆弱度的研究大多为定性分析，定量研究相对较少，且多尺度影响因素考量更加缺乏[15-17]。景观格局指数计算受空间粒度和幅度的影响较大，景观空间异质性会随空间粒度或幅度的改变而改变。空间尺度的选择会造成景观格局信息不同程度的变化响应，当研究尺度和研究对象的本质特征与研究区相符合时，景观格局指数才能将其景观格局特征更好地显示和反映出来[18]。可见，适宜的空间尺度对反映景观格局状况和开展景观生态环境研究至关重要。因此，本研究从探索景观格局脆弱度的最佳空间尺度出发，通过对景观格局脆弱度评价结果进行深入挖掘，以更加准确地反映区域景观格局脆弱度的时空变化信息。

招远市作为全国综合实力百强县市，其矿产资源丰富，经济活动密集，人为因素对景观生态环境的影响超过自然自我调节能力，成为了生态环境演变的主要推动力，因此亟需对招远市景观格局脆弱度进行分析与评价。招远市作为沿海典型中小型城市的缩影，研究价值较高，通过对该地区景观格局脆弱度的时空分异特征进行研究，以期对此类沿海资源富集区的合理开发和规划提供支持和服务。

1 数据来源与研究方法

1.1 研究区概况

招远市(120°08′～120°38′E、37°05′～37°33′N)位于华东地区胶东半岛西北端，隶属于山东省烟台市(见图1)，全市总面积约为1 432.37 km2。招远市地处胶东低山丘陵地带，西北濒临渤海，海岸线长约为13.5 km。该地区属暖温带季风区大陆性半湿润气候，四季分明，光照充足。境内矿藏资源丰富，以金矿和银矿为主，被称为“中国金都”。

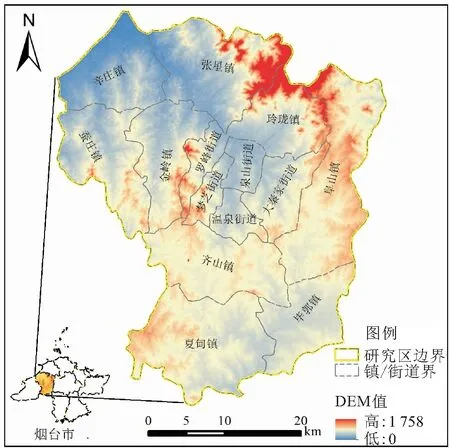
图1 研究区地理位置图Fig.1 Geographical location of the study area

1.2 数据来源

本研究使用的招远市2008年、2013年、2018年三期土地利用数据来源于土地二调及土地利用历年变更调查矢量数据库。参照《土地利用现状分类》(GB/T 21010—2017)，将招远市土地利用类型划分为耕地、林地、草地、水域、城镇工矿用地和未利用地6大类，得到招远市三期景观类型分布图。选用土地利用数据可有效规避遥感影像分类时地物判读不准确和Kappa系数大小的影响，从而提高景观格局脆弱度的分析精度，使所得结果更加准确。

1.3 研究方法

通过拐点识别法和信息损失评价模型并结合半变异函数确定最佳分析尺度，并基于最佳分析尺度选取科学适宜的景观格局指数，构建区域景观格局脆弱度评价模型，进而利用空间自相关理论，探究其时空演变特征。

1.3.1 空间尺度选取方法

(1) 空间粒度的选取。空间粒度是指景观中可辨别最小单元的长度和面积等，景观格局指数对空间粒度具有很强的依赖性，景观格局指数的空间异质性会随着空间粒度的变化而改变，即景观格局的空间粒度效应[19]。本研究借助拐点识别法和信息损失评价模型确定最佳景观分析的空间粒度。其中，信息损失评价模型可表示为

(1)

(2)

式中：M表示区域景观面积的损失值(%)；P为精度损失百分比(%)；Ab为所有景观类型该评价指标的基准数据值之和(km2)；Agi表示第i类景观类型空间粒度变化后的景观面积(km2)；Abi表示第i类景观类型空间粒度变化前的景观面积(km2)；n表示景观类型的总数目(个)。

(2) 幅度的选取。基于最佳空间粒度，采用网格分析法确定最佳幅度[20]。首先利用ArcGIS依次生成0.5 km、1 km、1.5 km、2 km、2.5 km、3 km的网格，并对土地利用栅格图分别进行掩膜提取；然后计算不同幅度栅格图的景观格局脆弱度指数，并将该指数赋值于网格中心点，再运用克里金插值法生成区域景观格局脆弱度空间分布图；最后利用半差异函数分析不同幅度下区域景观格局脆弱度指数，得出最佳幅度。其中，半变异函数[21]可表示为

(3)

式中:γ(h)为样本距为h的半方差值;h为样本距(变程)；Z(xi+h)为xi+h位置处的生态脆弱性值；Z(xi)为xi位置处的生态脆弱性值；N(h)为间距为h的样本对总个数。

1.3.2 景观格局脆弱度评价模型构建

景观格局脆弱度指数(LVI)是衡量景观生态脆弱性的指标，主要由景观敏感度指数(LSI)和景观适应度指数(LAI)构成[22][见公式(4)],其值的大小是区域景观格局生态脆弱性的定量表达。景观敏感度指数(LSI)是用来表示生态环境问题发生的难易程度，其变化速率越快，景观敏感性越强，其由景观干扰度指数(Ui)和景观易损度指数(Vi)构成[见公式(5)]。其中，景观干扰度指数(Ui)是指对外界干扰的变化程度，通常采用与干扰密切相关的景观类型破碎度(Ci)、分维数(Fi)和优势度(Di)3种指数来构建[见公式(6)]，权重系数为a、b、c，分别设定为0.5、0.3和0.2[23]；景观易损度指数(Vi)是土地利用易损程度与景观类型的有效结合，借鉴前人的研究成果，将景观类型易损度[24]划分为6个相对权重值，即未利用地为7、林地和草地为5、耕地为3、建设用地和水域为1。景观适应度指数(LAI)是用来表示景观在受外界干扰时表现出的适应与恢复能力，其与景观的结构、功能、多样性以及分布均匀程度紧密相关，本文结合招远市实际情况，选用相对斑块丰度指数(RPR)、Simpson多样性指数(SIDI) 和香农均匀度指数(SHEI)来构建[见公式(7)]。具体计算公式如下：

LVI=LSI×(1-LAI)

(4)

(5)

Ui=aCi+bFi+cDi

(6)

LAI=RPR×SIDI×SHEI

(7)

式中:n为景观类型数目(个)；i为景观类型。

1.3.3 空间自相关分析方法

空间自相关分析是空间数据分析方法和技术的集合，应用于景观生态脆弱性评价中，可以反映景观生态脆弱性的空间集聚特征，揭示其内在的变化规律。空间自相关性分析可分为全局和局部两种指标，全局自相关表示聚集效应是否存在于整个空间区域；而局部自相关用来衡量单元之间的空间差异程度和显著性[26]。

2 研究结果与分析

2.1 最佳研究尺度推绎

2.1.1 最佳空间粒度分析

以招远市三期土地利用数据为基础，首先以30 m为起点，300 m为终点，间隔30 m，将每期矢量数据栅格化生成10幅不同空间粒度的栅格图；然后分别选取斑块数量(NP)、斑块密度(PD)和周长面积分维数(PAFRAC)3种类型水平指数以及香农多样性指数(SHDI)、香农均匀度指数(SHEI)和分离度指数(DEVISION)3种景观水平指数，通过对选取的景观格局指数进行计算及分析，最终得出合适的空间分析粒度[27]，其结果见图2和图3。

(1) 景观格局指数空间粒度效应分析。由图2和图3可知：研究区三期景观格局指数随空间粒度增大的变化趋势大致相同，但同一时期各景观格局指数的变化有各自的特点，大致表现为3种状态：①斑块数量(NP)、斑块密度(PD)和分离度指数(DEVISION)的变化呈现一致性，表现出明显的空间粒度效应，其中各景观类型的NP和PD随空间粒度的增加逐渐递减，在空间粒度为30～90 m之间NP和PD值出现大幅度下降，在空间粒度为90～150 m之间其值下降幅度逐渐减小，在空间粒度为150 m后其值降幅趋于稳定；DEVISION整体呈下降趋势，在空间粒度为90～120 m之间DEVISION值出现一次小幅度回升，而后又继续下降；②各景观类型的周长面积分维数(PAFRAC)随空间粒度增加的变化趋势不明显，基本无规律可循，说明空间粒度效应不敏感；③香农多样性指数(SHDI)和香农均匀度指数(SHEI)随空间粒度增加的变化趋势比较平稳，仅出现小幅度波动，SHDI和SHEI值从空间粒度为30 m开始缓慢上升在空间粒度为90 m处出现第一次峰值，随后又出现不同程度波动，在空间粒度为210 m处达到最低值。

图2 2008—2018年研究区三期类型水平指数(NP、PD、PAFRAC)随空间粒度的变化曲线Fig.2 Change curves of type level indexes with spatial granularity at three phases from 2008 to 2018

图3 2008—2018年研究区三期景观水平指数(SHDI、SHEI、DEVISION)随空间粒度的变化曲线Fig.3 Change curves of landscape adaptability indexes(SHDI、SHEI、DEVISION) with spatial granularity at three phases from 2008 to 2018

(2) 最佳空间粒度的选取。随着空间粒度的增加，各景观类型出现了空间尺度拐点，这是由于栅格化过程中，矢量数据边界变化引起相邻斑块属性发生变化，从而导致景观格局指数发生相应的变化[28]。2008—2018年研究区三期景观面积损失值随空间粒度的变化曲线，见图4。

由图4可知：研究区景观面积损失值随空间粒度的增加整体呈上升趋势，表明景观信息量损失随空间粒度的增加不断增大。根据空间尺度拐点分布情况可以看出，在空间粒度为60～90 m处出现了第一空间粒度域，在90 m处景观面积损失达到最小值。景观格局指数最佳空间粒度通常选取第一空间粒度域内中等偏大的空间粒度[29]，故综合景观格局指数的空间粒度效应和空间粒度变化过程中景观信息量损失的原则，选取90 m为最佳空间分析粒度，既能很好地反映景观特征，又能避免计算冗余。

图4 2008—2018年研究区三期景观面积损失值 随空间粒度的变化曲线Fig.4 Change curves of loss value of landscape area with spatial granularity from 2008 to 2018

2.1.2 最佳幅度推绎

景观格局脆弱度由多种景观格局指数构成，不同景观格局指数对幅度变化的响应也有一定的差异[30]。所以，幅度选取对景观格局脆弱度的计算结果有极大的影响。以研究区2018年景观类型分布图为实验数据，建立边长为0.5 km、1 km、1.5 km、2 km、2.5 km、3 km的网格，计算不同景观类型网格下的景观格局脆弱度。本文运用GS+软件，借助半变异函数理论，根据复相关系数(R2)，并考虑综合残差(RSS)、块金值(C0)和变程(A0)选取最佳变异函数模型，分析不同幅度下景观格局脆弱度的空间异质性，进而获取适宜的景观格局脆弱度研究幅度。不同幅度下研究区景观格局脆弱度的半变异函数拟合模型参数，见表1。

由表1可知：幅度为0.5 km时，C0、C0+C值最小，说明该幅度空间效应不明显，空间变异程度较低；幅度由0.5 km到2 km，C/(C0+C)值上升，说明因自相关引起的空间异质性增强；幅度由2 km到3 km，C0值增加，C/(C0+C)值下降，说明块金效应增强，由随机部分造成的空间异质性不断增强；随着幅度的增加，该尺度内部更小尺度空间变异特征将被掩盖，其误差以块金效应体现出来。因此，幅度为2 km能够较直观地反映研究区景观格局脆弱度的空间变异情况。

表1 不同幅度下研究区景观格局脆弱度半变异函数拟合模型参数Table 1 Fitting model parameters of semi-variogram of landscape pattern vulnerability indexes under different amplitudes

2.2 景观类型变化特征分析

本文运用ArcGIS对研究区三期景观类型分布图(见图5)进行叠置分析，可得到2008—2013年、2013—2018年两个阶段研究区的景观类型面积转移矩阵，见表2。

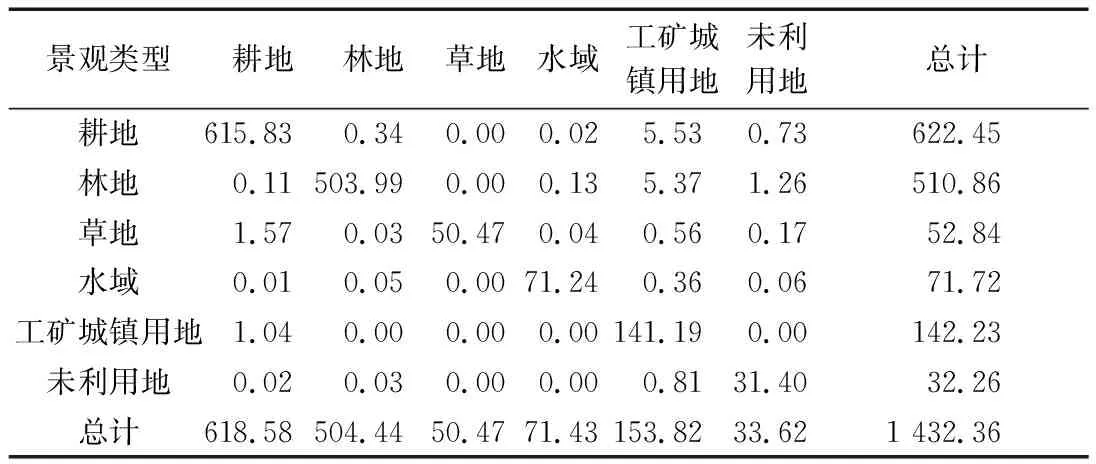
表2 2008—2013年研究区三期景观类型面积转移矩阵(单位：km2)Table 2 Transition matrix of landscape types at three phases from 2008 to 2013 in the study area (unit:km2)

图5 2008—2018年研究区三期景观类型分布图Fig.5 Distribution map of landscape types in the study area at three phases from 2008 to 2018

由表2可知：

(1) 2008—2013年间，研究区景观类型的变化主要表现为“两升四降”的变化趋势，即耕地、林地、草地和水域景观类型的面积下降，工矿城镇用地和未利用地景观类型的面积上升。其中，耕地和林地景观类型的面积明显减少，分别减少3.88 km2和6.41 km2；工矿城镇用地景观类型的面积明显增加，增加11.58 km2。耕地和林地面积的减少主要转换为工矿城镇用地，说明在这五年期间随着经济的快速发展，城镇化较明显；但同时林地、草地人为破坏严重，表现为林地和草地向未利用地的转化，说明存在人为破坏和部分砍伐现象；水域面积减少主要转化为林地、工矿城镇用地和部分未利用地，说明在人为干扰下出现部分水土流失问题。

(2) 2013—2018年间，研究区景观类型的变化与前五年大致类似，工矿城镇用地景观类型的面积明显增加，城镇化现象明显，耕地和林地向未利用地的转化有所减少，说明人为破坏现象有所缓解，并积极开展了植树造林活动，这与国家大力推进生态环境治理有很大的关系。

表3 2013—2018年研究区三期景观类型面积转移矩阵(单位：km2)Table 3 Transition matrix of landscape types at three phases from 2013 to 2018 in the study area (unit:km2)

2.3 景观格局脆弱度时空演变特征分析

为了更好地可视化研究区景观格局脆弱度等级差异，本文将计算出的研究区景观格局脆弱度值赋予各个网格中心点，并运用普通克里金差值法生成研究区三期景观格局脆弱度空间分布图，同时采用自然断点法将研究区景观格局脆弱度计算结果划分为低、较低、中等、较高、高5种脆弱度等级，并统计研究区三期不同景观格局脆弱度等级的面积占比，其统计结果见图6。

图6 2008—2018年研究区三期景观格局脆弱度等级 的面积占比Fig.6 Distribution of grades of landscape pattern vulnerability at three phases from 2008 to 2018

由图6可见：研究区景观格局脆弱度等级面积占比呈正态分布，中等脆弱度区面积最大，面积占比始终高于其他脆弱度等级；研究区3个时期景观格局脆弱度整体来说较为稳定，2008年以低等级脆弱度为主，其中低、较低和中等脆弱度区面积占研究区总面积的75%以上，2008年景观格局高脆弱度区的面积占比达到最低；之后的十年中，区域整体景观格局脆弱度呈恶化趋势，中等脆弱度区面积变化不显著，出现小幅度波动，低和较低脆弱度区面积占比不断下降，逐渐向较高和高脆弱度区转化，2018年景观格局高脆弱度区的面积占比达到最高，占研究区总面积的10%，说明区域景观格局脆弱程度不断加剧。

景观格局脆弱度受不同时期土地利用所引起的景观格局及其组分变化的综合影响，表现出区域变化的特点。2008—2018年研究区三期景观格局脆弱度分区图，见图7。

由图7可见：研究区景观格局高脆弱度区集中分布在西北的辛庄镇、张星镇、蚕庄镇、金岭镇和西南的齐山镇、夏甸镇、毕郭镇等镇域结合部，低脆弱度区主要分布在东部和南部，其他零星分布在研究区内，呈现区域交错分布状态；研究区低脆弱度区景观类型主要为林地和部分耕地，因林地和耕地分布较为有序，特别是东部景观类型相对稳定，景观适应度较高，加之此区域距离中心城区较远，受人为干扰的影响小，所以呈现出低脆弱度状态；而研究区较高和高脆弱度区草地、耕地和工矿建设用地交错分布，部分河流沿岸存在滩地、沼泽和盐碱地等未利用地，斑块本身比较破碎，所以呈现出高脆弱度状态。总体来说，研究区景观格局脆弱度的空间格局与景观类型的分布变化具有较强的耦合关系。2008年以来，随着城乡建设的不断发展，研究区人类活动的干扰进一步增强，人口密集、社会经济发展较快的地区不断向四周扩张，用地类型随着建设区各自拓展，西北部由于工业开发区建设，局部景观格局遭到破坏；蚕庄镇、玲珑镇、张星镇等地区由于矿产资源开采，使得原有景观生态空间发生变化，造成不同用地类型的破碎化程度加剧，景观格局脆弱度加剧。虽然研究区人为影响为主导因素，但人类的干预并非全是消极的影响，有必要在自然演变的过程中，加以合理的人为干预，用于提高景观格局脆弱度的稳定性。其中，对于景观格局低脆弱度区域，可通过生态资源有效配置和景观格局分布来优化生态系统功能，如加强绿地斑块覆盖度、提高景观类型丰富度、增加区域物种丰富度、优化生态系统抗风险能力等；而对于草地、耕地和工矿建设用地交错分布的景观格局高脆弱度区域，可通过调整土地结构，定期进行河道疏通来降低河流漫滩危害，将建设用地向集中有序方向发展，做好矿区合理开采和矿区恢复工作，做好耕地生态防护林建设，以此来增强生态系统的稳定性，提高生态适宜性。通过人为干预，使得景观格局脆弱度更加稳定，以增强自然界抗干扰能力，保证生态系统合理有序演变，提高生态环境安全性。研究区为此类沿海典型城市的缩影，对此类城市合理开发与规划具有重要的参考意义。

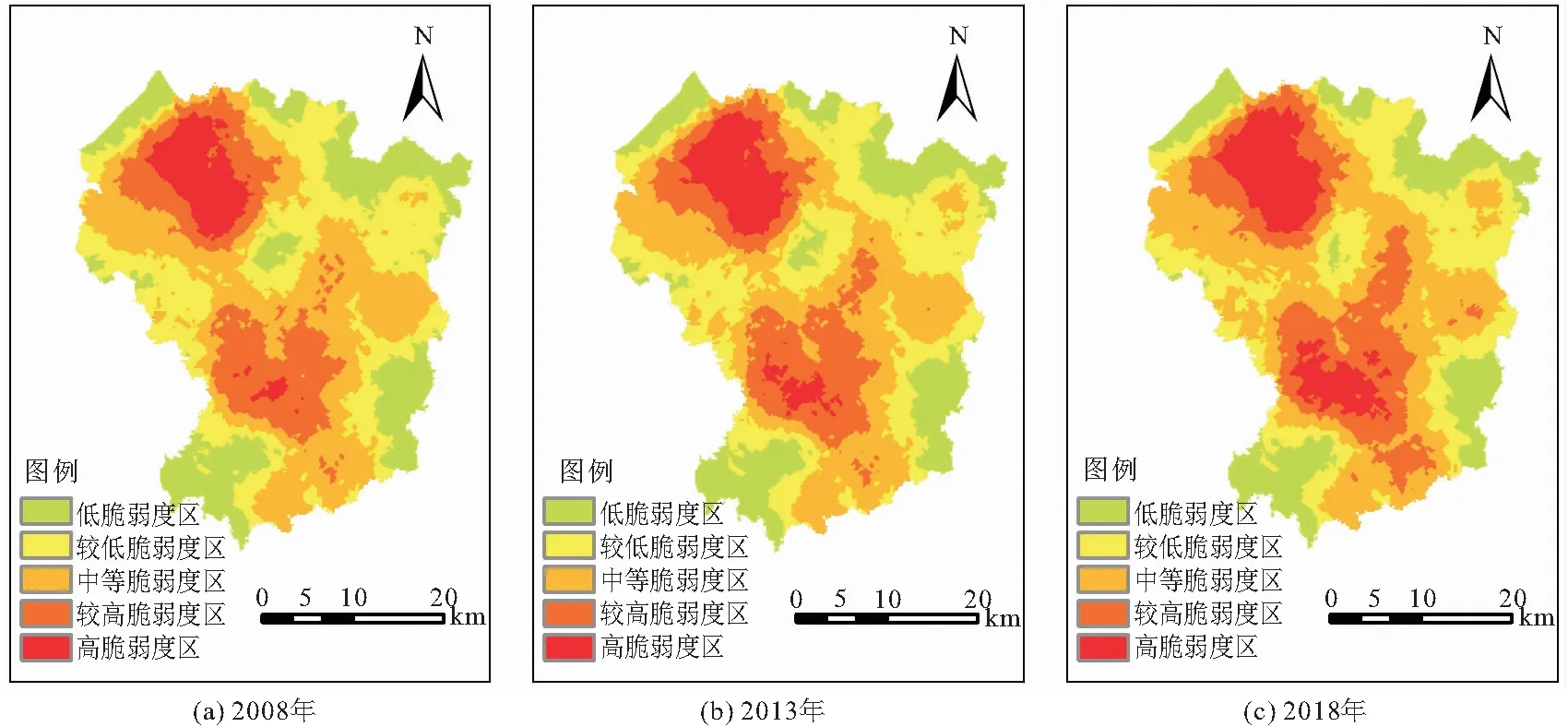
图7 2008—2018年研究区三期景观格局脆弱度分区图Fig.7 Distribution of landscape pattern vulnerability at three phases from 2008 to 2018 in the study area

2.4 景观格局脆弱度空间关联分析

为了更好地了解研究区景观格局脆弱度空间分异和聚类特征，本文利用GeoDa软件计算了研究区三期景观格局脆弱度的全局Moran′sI指数,其计算结果见表4。

表4 研究区三期景观格局脆弱度的全局Moran′s I指数计算结果Table 4 Global Moran′s I coefficient of landscape pattern vulnerability at three phases in the study area

由表4可知：研究区三期景观格局脆弱度的全局Moran′sI指数均大于0，p值均小于0.01，z得分分别为8.696 8、8.518 9、8.612 5，说明研究区不同时期的景观格局脆弱度呈显著正相关，其空间分布不是随机的，有明显的空间聚集性特征；2008年、2013年和2018 年三期景观格局脆弱度的全局Moran′sI指数分别为0.315 6 、0.308 5和0.311 5，其数值波动范围小，景观格局脆弱度空间自相关性保持稳定，空间集聚现象变化明显。

局部Moran′sI指数统计可以揭示空间相邻区域要素的空间关联模式，以便进一步展开空间局部自相关性分析，经计算生成了研究区三期景观格局脆弱度的局域空间自相关分布图，见图8。

由图8可见：2008—2018年3个时期，研究区高—高值、低—低值聚集区分布变化不大，表现为相对集中，其中高—高值聚集区主要分布在西北和西南，并有不断向西北蔓延的趋势，低—低值聚集区的分布较为分散；高—低值、低—高值聚集区分布极少，零星分布于研究区内，这与克里金插值结果表现出一致性。

图8 2008—2018年研究区三期景观格局脆弱度的局域空间自相关分布图Fig.8 Local spatial auto-correlation distribution map of landscape pattern vulnerability at three phases from 2008 to 2018 in the study area

3 结论与建议

本文采用景观生态学和空间分析理论，基于最佳分析尺度，选取适宜的景观格局指数，构建了景观格局脆弱度评价模型，对研究区景观格局生态脆弱性进行了评价，分析了2008—2018年间研究区景观格局脆弱度的时空演变特征，以及空间关联性和空间异质性，并通过对研究区不同尺度的实证研究，对比得出了最佳研究尺度，很好地揭示了在复杂的环境条件影响下景观格局脆弱度的时空变化机理，验证了选取合适尺度对景观格局脆弱度研究的必要性。主要得到如下结论：

(1) 研究区3个时期类型水平指数和景观水平指数在空间粒度为90 m处出现了明显的拐点，表明景观格局指数存在明显的尺度效应；信息损失评价模型分析显示，60～90 m为最佳空间粒度域，综合确定90 m为研究区最佳空间分析粒度；半变异函数模型分析显示，2 km幅度能够消除随机因素对景观格局脆弱度的影响，较为直观地反映其空间变异情况，是研究区景观格局脆弱度理想的研究尺度。

(2) 2008—2018年间，研究区整体景观格局脆弱度逐年上涨，表现为低和较低脆弱度区面积占比逐渐降低，较高和高脆弱度区面积占比不断上升，景观格局脆弱程度不断加剧；在空间上高脆弱度区主要分布在研究区西北和西南镇域结合部，在十年间，由于工矿建设用地粗放式扩张，原有景观生态空间遭到破坏，斑块破碎程度加剧，使研究区景观格局脆弱度不断加剧。

(3) 2008年、2013年和2018年研究区景观格局脆弱度的全局Moran′sI指数均大于0，表现出显著的正相关，景观格局空间聚集性特征明显；局域空间自相关分布图显示，高—高值、低—低值聚集区分布具有明显的空间关联性，其与克里金插值表现出一致性。

区域景观生态脆弱性与其景观类型和景观格局有很强的关联性，景观格局脆弱度的变化与城市扩张趋势以及土地利用模式密切相关，本文方法对研究景观格局脆弱度的时空分布特征与区域自然和城市发展情况较为贴切。十年间，研究区景观格局脆弱度受自然因素和人为因素的影响，景观格局脆弱程度上升，其中人为影响是较强的驱动因素，但人类的干预并不全是消极的影响，植树造林、科学合理的规划发展等保护措施可使斑块形状更加规则，景观分布更加均匀，资源配置更加合理，有利于区域生态系统的高质量发展。因此，有必要在自然演变的过程中，加以合理的人为干预，用来提高景观格局脆弱度的稳定性。但本文方法中景观干扰度指数权重的赋值具有一致性，对于不同的景观类型的干扰度指数所参与组合的权重赋值应根据各自的生态效应特征进行有差别的处理；景观易损度指数权重的赋值反映的是景观类型相对易损程度，如何采用更加合理的赋值方法也有待进一步探讨。此外，驱动因素对景观格局脆弱度的影响也具有阶段性和区域性特征，今后应基于生态过程机理的驱动力方面开展更为深入的研究。