基于粒子群优化层次分析法的LNG槽车风险评价
李 潇,张 毅,汪 涛,李朝阳
(上海交通大学船舶海洋与建筑工程学院,上海 200240)
在我国石油天然气基础设施改革的背景下,原来隶属于“三桶油”的液化天然气(LNG)接收站逐步向社会资本开放,往来各接收站装卸LNG的槽车数量与之前相比将大大增加,车辆构成也将更为复杂,现行的槽车安全管理体系已经逐渐难以适应未来灵活而复杂的LNG接收站内物流环境。
LNG槽车作为移动危险源,有关学者对其安全管理做了深入研究。如张淑淑等[1]详细论述了LNG在储运过程中的事故类型及特点;宋贺[2]利用关联规则、解释结构模型和贝叶斯网络,构建了危险货物道路运输事故的贝叶斯网络预测模型;林现喜等[3]结合LNG槽车风险类型及防控措施,提出了基于全过程风险管控的LNG槽车安全管理体系;岑康等[4]对LNG加气站槽车卸车直供过程中不同类型的泄漏事故进行了模拟分析,对事故后果扩大程度进行了定量分析。关于层次分析法的计算与应用,国内外学者也做了大量的研究。如郭金玉等[5]论述了传统层次分析法在矿山安全、交通安全等6个研究领域的应用;冯致学等[6]提出一种改进的3标度层次分析法,并对电网遭受地质灾害脆弱性指标进行了评价;郑重等[7]提出一种避免对判断矩阵进行一致性检验的改进层次分析法,用于对影响矿山边坡稳定性的因素进行评价;牛东翔等[8]利用层次分析法对LNG船舶的运营状况进行了评价;崔春英等[9]利用层次分析法结合模糊综合评价法建立了LNG接收站的安全评价模型。但上述这些评价方法在计算过程中涉及对判断矩阵的调整,同时由于自身计算精确度不高,导致最终评价结果的准确性不足。粒子群算法自20世纪90年代被提出以来,因其良好的寻优性能,许多学者对其发展与应用进行了研究。如Jiang等[10]借助随机过程理论,给出了粒子群算法的随机收敛条件以及相关参数选择准则;Clerc等[11]总结了粒子群系统的运行特征,建立了包含决定粒子群算法收敛性参数的广义模型,为该算法在多维度复杂空间中的应用提供了基础。在粒子群算法的实际应用中,不少学者对其进行了改进,同时为了避免算法陷入局部最优解并提高求解精度,陈博文等[12]提出了一种总结性自适应变异的粒子群算法;简文星等[13]将粒子群算法用于锚拉桩桩身参数的优化设计,并取得了良好的效果;杨玉梅等[14]利用粒子群算法对航运安全投入模型进行了优化,为航运企业安全投入决策提供了可靠的模型依据。
基于上述研究,本文提出一种基于粒子群算法优化的层次分析法,并利用该方法对影响LNG槽车充装安全性的众多风险因素的权重进行了计算,用于帮助LNG接收站运营单位细化日常的安全管理体系,以增强LNG接收站内槽车运行的安全性。
1 LNG接收站槽车充装风险评价指标体系建立
1.1 评价指标的选择
本文围绕LNG接收站内槽车充装整个过程中的人员技术水平与专业素质、设备可靠性与槽车自身安全性、LNG接收站内外环境、现场安全管理水平4方面选择评价指标。人是安全管理工作的核心,人员技能与素质是现场安全运行的前提,司乘人员培训与日常装车安检则是防范现场人员不安全行为的有效措施,业务管理人员处置突发事件的能力是降低事故损失的重要保障。从设备可靠性的角度分析,LNG槽车储罐内操作压力逐渐升高,严重时会导致储罐超压损坏,可燃气体泄漏,甚至发生火灾等严重后果[15],因此对LNG槽车储罐罐压的监测是LNG接收站内安全工作的重点。设备越先进,安全仪表系统的重要性越高,其中DCS系统(分布式控制系统)、SIS系统(安全仪表系统)可以有效地监测设备运行状态与异常;FGS系统(火灾报警和气体检测系统)的完好性对槽车充装本质安全具有重要意义;静电接地连锁报警系统可以在槽车充装过程中及时避免静电火源;槽车装车事故多发的主要原因是接头问题[16],而装车撬上的防拖拉装置可有效避免槽车充装过程中的安全事故。另外,对LNG接收站内外环境的评估是完善现场安全管理制度与制定应急预案的基础;而槽车整个装车环节中安全管理的科学性与合理性又决定了现场本质安全的效果与运行效率[17]。因此,本文最终从人员、设备、环境和管理四个方面选择了15项评价指标。
1.2 评价指标体系的建立
槽车在LNG接收站内的充装过程涉及到多个环节、多个部门,主要包括核对装车计划、到站后的车辆安检与充装、贸易计量等。由于LNG接收站内场地容量有限,大部分槽车到达LNG接收站周边后往往无法直接进入充装区,而是在附近等待调度,这也增加了装车过程中安全管理的难度。本文以人、机、环、管4个因素作为一级评价指标,在每个一级评价指标之下选择3至5个关键因素作为二级评价指标,建立了LNG接收站槽车充装风险评价指标体系,如图1所示。
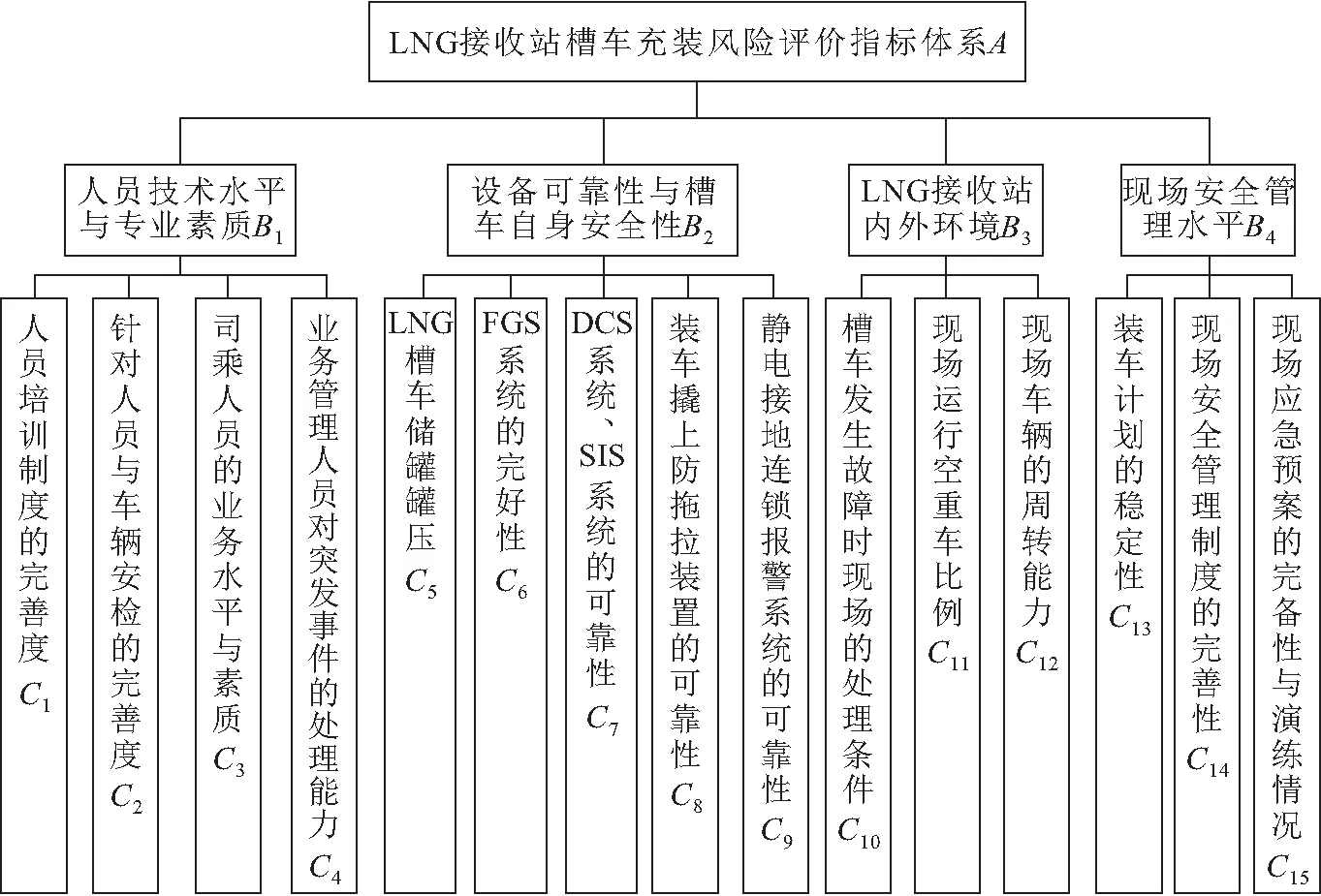
图1 LNG接收站槽车充装风险评价指标体系Fig.1 Risk evaluation index system of LNG terminal tanker filling
2 评价方法
2.1 层次分析法
层次分析(Analytic Hierarchy Process,AHP)法是运筹学中一种将目标按照影响因素分解为若干层,再通过模糊量化的方法计算每层中各指标的权重以及各指标在整个目标体系中权重的方法,在多目标、多准则、多时期的系统评价中有着广泛的应用[18]。使用AHP法首先要建立各层影响因素的判断矩阵,然后根据判断矩阵对各因素的权重进行求解[19-20],但当判断矩阵中数据较多时,使用传统的AHP法会导致求解过程中计算量大大增加,同时计算过程中还需要不断地对判断矩阵进行调整以保证其一致性,从而影响了整个评价结果的客观性。
2.2 粒子群算法
粒子群优化(Particle Swarm Optimization,PSO)算法也称粒子群算法是一种全局进化算法,这种算法计算过程简单且需要调整的参数少,适用于对复杂问题求最优解。PSO算法最初由Eberhart和Kennedy两位博士于1995年提出[21],其构想源于对鸟群捕食行为的观察:假设食物位置固定,鸟群中的每只鸟会根据自身距离食物的位置和鸟群距离食物的位置这两个参数来不断修正自己位置和飞行速度,直到聚集到食物位置。在复杂问题的求解过程中,可将鸟比作粒子,每个粒子有“位置”和“速度”两个基本参数,当用于评价整个系统的目标函数已知时,粒子在每一轮计算中逐渐调整自身的位置与速度以适应目标函数,直到获得目标函数最优解。本文利用AHP法构建影响因素判断矩阵,将判断矩阵中各影响因素的权重值看作粒子不同维度的坐标值,通过对粒子维度坐标不断地迭代,最终计算出每层判断矩阵中各影响因素的最优权重值,具体计算步骤如下:
(1) 确定每个粒子的维度。本文的关键在于对每个判断矩阵中各影响因素的权重进行求解,于是结合PSO算法的特点,将这些当前未知的权重用每个粒子的维度坐标来表示,经过迭代求得最优粒子后,最优粒子每个维度的坐标值便是判断矩阵中各影响因素的权重值。因此,每个粒子的维度需要与当前判断矩阵中影响因素的个数相等,同时这个维度也是粒子所在空间的维度,即每个粒子的维度等于下面公式(4)中权重参数wi的个数。
(2) 设定粒子个数与每个粒子的初始位置xi(0)和速度vi(0)。粒子个数可根据粒子维度与计算规模设定,粒子数量越多计算效率越高,本文取20个粒子进行迭代;粒子初始位置和速度表征了粒子在空间中的初始坐标值和坐标变化幅度,需要根据具体问题可行域设定,本文中判断矩阵中各影响因素的权重值在0到1之间,可行域为[0,1],因此xi(0)和vi(0)取0到1之间的随机数。
(3) 根据粒子每一轮迭代返回的目标函数值得到本轮粒子个体最优位置和全局最优位置。如:第t轮迭代单个粒子目标函数值最优时,粒子i的坐标为其个体最优位置pi(t);本轮所有粒子中目标函数值最优的粒子对应的坐标作为全局最优位置pg(t)。
(4) 根据PSO算法的进化方程,更新粒子下一轮迭代的坐标与速度,其计算公式如下:
xi(t+1)=xi(t)+0.1vi(t+1)
(1)
vi(t+1)=wvi(t)+c1r1(t)[pi(t)-xi(t)]+
c2r2(t)[pg(t)-xi(t)]
(2)
式中:将粒子运动的时间步长取0.1,xi(t+1)、xi(t)分别表示第i个粒子t+1、t时刻在空间中的位置坐标;vi(t+1) 、vi(t)分别表示第i个粒子t+1、t时刻在空间中的速度;w为惯性权重值,表示每个粒子对上一时刻运动状态的继承,取值越大表示全局寻优能力越强,取值越小则表示局部寻优能力越强,由于本文可行域较小,故w取值为0.1;c1、c2分别为群体学习速率和个体学习速率,表示粒子对上一时刻自身经过的最优化位置和群体经过的最优位置的重视程度,Shi等[22]认为它们的值应相等并建议取值为0.2;r1、r2为0到1之间的随机数,用于增加粒子运动过程中速度变化的随机性。
(5) 重复上述步骤(2)至(4),按照预先设定的迭代次数对粒子群进行迭代,计算得到系统最优点位置坐标pgbest(t),最终输出各影响因素的最优权重值wi,也可在程序中设定粒子变异系数,以增加计算速率。
2.3 基于粒子群算法优化的层次分析法(即PSO-AHP法)
2.3.1 PSO-AHP法目标函数
如上所述,PSO算法找寻最优解首先需要确定一个合适的目标函数以检验粒子的优劣,并以目标函数返回值作为粒子下一轮迭代的参照。在AHP法中,如果判断矩阵An×n可以完全满足一致性,则以下公式(3)中等式成立,本文构建的判断矩阵为正互反矩阵,虽然不能完全满足判断矩阵的一致性,但公式(3)等式中左边的数值越小,说明判断矩阵的一致性程度越高,因此选择各影响因素的权重wi作为自变量,以判断矩阵的一致性作为判定粒子优劣的标准建立目标函数[见公式(4)],将各影响因素的权重求解问题转化为令目标函数值最小的优化问题,以此将PSO算法与AHP法结合起来,具体计算公式如下:
(3)
(4)
式中:W为评价指标体系中每层影响因素权重列向量;aik为判断矩阵中的元素值;wi为影响因素的权重值,即向量W中的元素值;n为影响因素的个数。
2.3.2 PSO-AHP法流程
PSO-AHP法将PSO算法的最佳寻优性能与传统AHP法的基本原理相结合,通过选取合适的目标函数将两者联系起来,从而快速求解判断矩阵中元素的权重,PSO-AHP法的流程见图2。

图2 PSO-AHP法流程图Fig.2 Flow chart of PSO-AHP algorithm
3 算例分析
中国石化天津LNG接收站是华北地区最大的LNG接收站之一,该接收站位于天津南港工业区内,于2018年初投产,设计周转能力为300×104t/a;槽车装车区设置20台装车撬,24小时装车,单台撬装车能力为20 t/h;LNG接收站内设有待装区,可容纳30台槽车,在站外5 km处设有槽车初检区,可容纳50台槽车,初检区至接收站的路况较差,行驶时间约40 min。本研究以天津LNG接收站为例,采用本文建立的LNG接收站槽车充装风险评价指标体系,利用PSO-AHP法对影响槽车充装安全性的关键因素进行风险评价,并确定各风险指标的权重,具体评价过程如下。
3.1 风险指标权重的计算
3.1.1 构建判断矩阵
(1) 风险指标评价。选择石化行业工作经验丰富的现场安全工程师1位、销售部安全总监1位,共计2位专家,根据天津LNG接收站槽车运行情况,对图1中风险指标的重要度进行打分,为方便专家打分,打分采用指标两两对比的原则。首先由专家对同一层次内的指标两两比较,按照重要程度对比可分为①极端不重要、②明显不重要、③同等重要、④明显更重要、⑤极端更重要5个等级,构建专家打分矩阵D。各指标重要程度对应的系数dij如下:
然后,以一级指标为例,专家1和专家2针对一级指标中4项风险因素B1、B2、B3、B4,专家具体打分结果如下:
(2) 判断矩阵构建方法。对专家的打分结果进行分析,构建同层次风险因素的重要度判断矩阵,并将专家打分矩阵D中的元素dij进行变换构建判断矩阵Ai,具体计算公式如下:
(5)
rmax=max{ri}
rmin=min{ri}
(6)
(7)
式中:dij为专家打分矩阵中的每个元素;n为专家打分矩阵的列数;ri为专家打分矩阵中每行元素之和。
以一级指标为例,根据专家打分矩阵D1、D2通过公式(5)和(7),可计算得到判断矩阵A1、A2:
3.1.2 利用PSO算法计算指标的权重
按照PSO算法流程,使用PSO算法对两位专家所构建的判断矩阵中各风险指标进行权重计算。以一级指标对应的判断矩阵为例,一级指标判断矩阵中含有4个风险因素,所以用MATLAB软件生成20个4维粒子,粒子维度范围在0到1之间;粒子初始速度参数与初始位置一致,速度变化范围设为[-0.1,0.1];根据公式(4)计算每一轮迭代过程中每个粒子的适应度函数值,输出群体最优点pg(t)和粒子个体最优点pi(t);根据公式(1)和(2)对每个粒子的位置与速度进行迭代,与此同时,算法的目标函数值随着粒子的每一轮迭代逐渐减小并趋于稳定,如图3所示;最终输出粒子最优位置坐标pgbest(t)并归一化,即为图1中一级指标各风险因素的权重。根据两位专家的打分情况,本文中4个一级指标的权重向量分别如下:

图3 PSO-AHP法逼近目标函数最优解的迭代过程Fig.3 Iterative process of approximating optimal solution of objective function by the PSO- AHP method
W1=(0.237 0.377 0.147 0.239)
W2=(0.269 0.214 0.178 0.340)
3.1.3 基于PSO-AHP法的指标综合权重计算
利用一级指标判断矩阵的构建与权重计算方法,可以根据两位专家打分结果分别计算出4组二级指标的权重,然后将4组二级指标的权重向量乘以其对应的一级指标权重值,得到二级指标中各风险因素在系统中的总权重Y1和Y2;考虑到两位专家的工作年限与业务内容的差异,对专家1的打分结果取0.75的权重,对专家2的打分结果取0.25的权重。最终,通过PSO算法与AHP法两种方法可得到的各指标的综合权重计算公式如下:
W=0.75Y1+0.25Y2
(8)
通过PSO-AHP法,可计算得到各指标对LNG接收站槽车充装安全性的影响程度即重要度排序。为了验证PSO-AHP法指标权重计算结果的准确性,将PSO-AHP法指标权重与改进的AHP法[7]指标权重的计算结果进行了对比,见表1。

表1 天津LNG接收站槽车充装风险指标权重的计算结果Table 1 Weight calculation result of risk indexes of tanker filling of the LNG terminal in Tianjin
3.2 评价结果分析与建议
通过上述计算,可以得出评价指标体系中15项风险指标对天津LNG接收站槽车充装安全性的影响程度大小,各风险指标权重分布见图4。

图4 天津LNG接收站槽车充装风险指标权重分布图Fig.4 Weight distribution of risk factors of tanker filling of the LNG terminal in Tianjin
由图4可见,对天津LNG接收站槽车充装安全性影响最大的5项风险指标分别为:①现场应急预案的完备性与演练情况C15;②装车撬上防拖拉装置的可靠性C8;③现场安全管理制度的完善性C14;④针对人员与车辆安检的完善度C2;⑤装车计划的稳定性C13。
综上分析可知,LNG接收站槽车充装过程中的安全性受到诸多风险因素的影响,本文通过对中国石化天津LNG接收站的案例分析,针对槽车充装安全管理提出了如下改进建议:
(1) 要始终将现场应急预案的完备性与演练情况放在安全管理的重要位置,并在实践中不断细化与更新现场应急预案的内容,同时需要特别注意极端条件下大规模突发事故的应急处置办法。
(2) 要注重LNG接收站内消防设施的日常维护和现场 LNG 充装设备的日常检修。
(3) 要加强LNG接收站内的安全管理以及对工作人员的安全教育,并在制定安全管理制度时注重科学性与实用性。
(4) 在实际运行过程中,槽车周转效率对LNG接收站槽车充装安全性有着潜在的影响,因此为了防止附近道路聚集大量槽车,在车辆调度过程中需结合销售计划的管控,以增强车辆到站的时序性。
4 结 论
本文以LNG接收站槽车整个充装流程中的风险因素为研究对象,采用基于粒子群算法优化的层次分析法对各风险因素进行了权重计算和重要度分析,并通过案例分析,对比了PSO-AHP法与改进AHP法[7]指标权重的计算结果。结果表明:两者计算结果相近,但相比于其他对判断矩阵求解的方法,PSO算法采用多个粒子迭代的方式直接对判断矩阵进行求解,大大提高了计算结果的精确度,且在求解过程中利用MATLAB编程,保证了求解速度。最后本文对影响LNG接收站槽车充装安全性的宏观因素进行了重要度分析,并根据分析结果提出了改进建议,可为新建LNG接收站的安全管理提供可借鉴的经验。

