固体火箭发动机多层结构超声信号传输的数学模型

郭旭飞

(1 吕梁学院物理系，山西 吕梁 033001；2 中北大学信息探测与处理山西省重点实验室，太原 030051)

0 引言

当前针对固体火箭发动机多层结构壳体的脱粘问题，主要研究都集中于技术测试与应用，理论上的分析与建模并不多见。段方勇等[1]采用传输矩阵法建立了多层结构超声回波幅度谱模型,分析了由不同材料构成的多层结构的幅频特性。张建生[2]提出了钢-橡胶多层结构的超声卷积模型，并采用同态滤波解卷积等信号处理方法分析界面脱粘的特征。简晓明[3]根据声压和质点速度在界面处的连续性推导了超声脉冲回波的解析表达式,并对二界面粘接情况进行了评价。Hägglund等[4-5]提出了参数模型，并推导出了模型参数的最大似然估计，然后用于广义似然比检验(GLRT)来检测多层结构中的缺陷。闫鑫[6]利用输入阻抗来描述多层结构的反射谱，并分析了界面粘接缺陷的反射谱特征。

在文献[2,5]的基础上，文中将多层结构的超声模型进行简化，并对部分公式进行修正，得到任意多层结构的超声信号传输的数学模型，为后续对多层结构进行信号分析与处理奠定理论基础。

1 多层结构的数学模型

1.1 线性系统

在系统识别中，被研究的材料或结构可以被视为线性系统，而传递函数可以描述线性系统的特征,即描述了输出信号y(t)和输入信号u(t)之间的关系，如图1所示。与时域分析相比，离散的频域分析有许多优点[7]。

图1 在时域和频域中的线性系统

输出和输入在频域的关系为:

Y(jω)=Htf(jω)U(jω)

(1)

式中:Y(jω)，U(jω)分别为输出信号和输入信号的傅里叶变换；ω为角频率。

1.2 单层结构超声传输模型

单层结构的超声传输模型如图2所示，为了描述方便，信号垂直输入，均在图中表示斜入射，且未考虑材料的衰减。

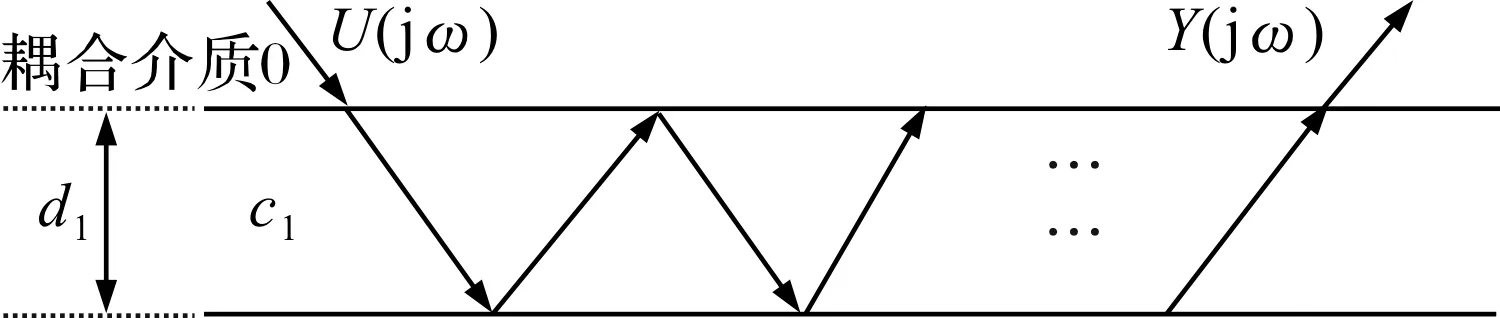
图2 单层结构反射信号传输示意图

当超声信号垂直入射到单层结构，在介质中会形成多层反射。

第一次反射为：

Y1(jω)=T01R12T10e-jωτ1U(jω)=T01T10R12e-jωτ1U(jω)

(2)

第二次反射为：

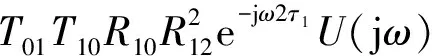
(3)

第三次反射为：

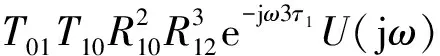
(4)

⋮

第n次反射为：

(5)

则第n次反射与第(n-1)次反射满足关系：

Yn(jω)=R10R12e-jωτ1Yn-1(jω),n≥2

(6)

式(2)～式(5)中:T为界面透射系数;R为界面反射系数;τ1为界面反射两次的时间，可表示为2d1/c1,d1为单层介质的厚度，c1为超声传播速度。单层结构总输出超声信号为：

(7)

进一步整理得到：

(8)

则单层结构的传递函数为：

(9)

式中，τ0为超声的时间延迟。由于一般耦合介质很薄，τ0影响可忽略，则

(10)

1.3 多层结构超声传输模型

对于多层结构，由于不同层之间非连续性声阻抗特性，所以超声信号存在多次反射和折射。从图3可以看到增加了层数使得信号传播路径复杂化。但其中每一层超声传播和单层介质类似，传递函数容易求出。只要求出任意层的传递函数，那么多层结构的传递函数是各层传递函数的级联。

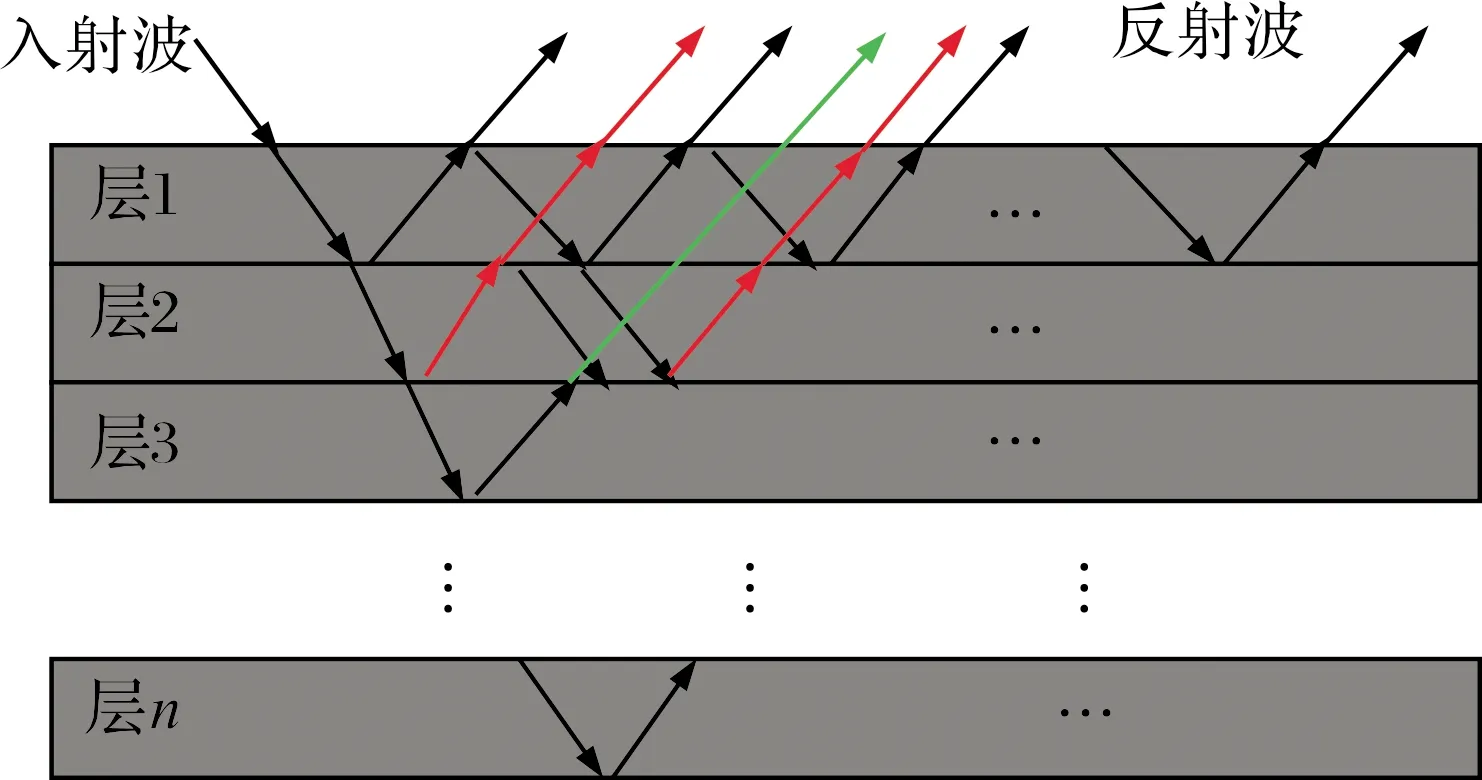
图3 多层结构超声信号传播示意图

假设第q层为多层结构中的任意一层(q>1)，则超声在其内部传输和接收分为3种情况：

1)信号从第(q-1)层下行入射到第q层，经多次反射，从第q层上行透射到第(q-1)层。

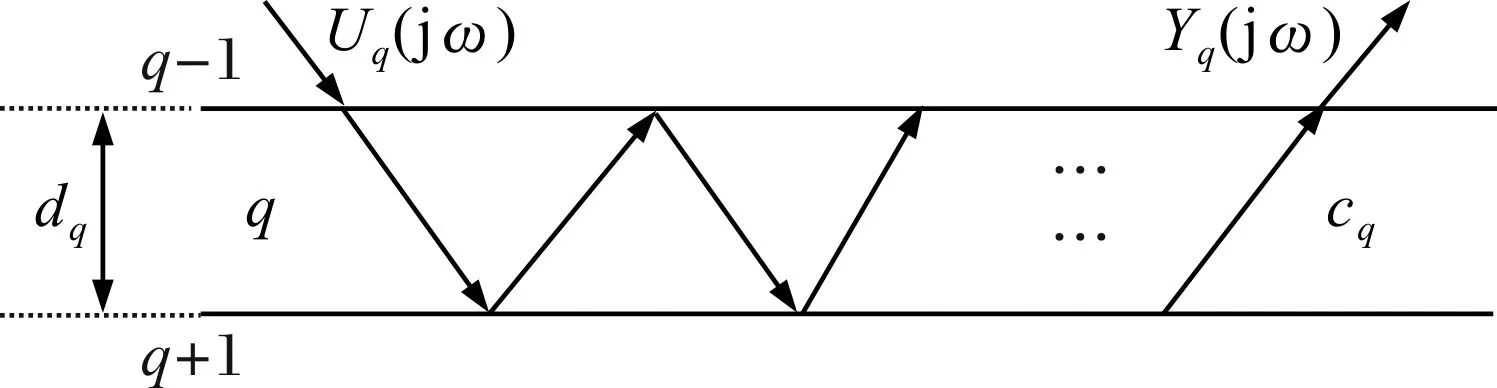
图4 信号从第(q-1)层下行到第q层，再上行到第(q-1)层传播示意图

这种情况与单层结构的超声传播类似，对应的传递函数为：

(11)

式中:τq为信号在上下界面依次反射一次的传播时间，可表示为2dq/cq,dq和cq分别为第q层的厚度和波速。

2)信号从第(q-1)层下行入射到第q层，经多次反射，从第q层下行透射到第(q+1)层。

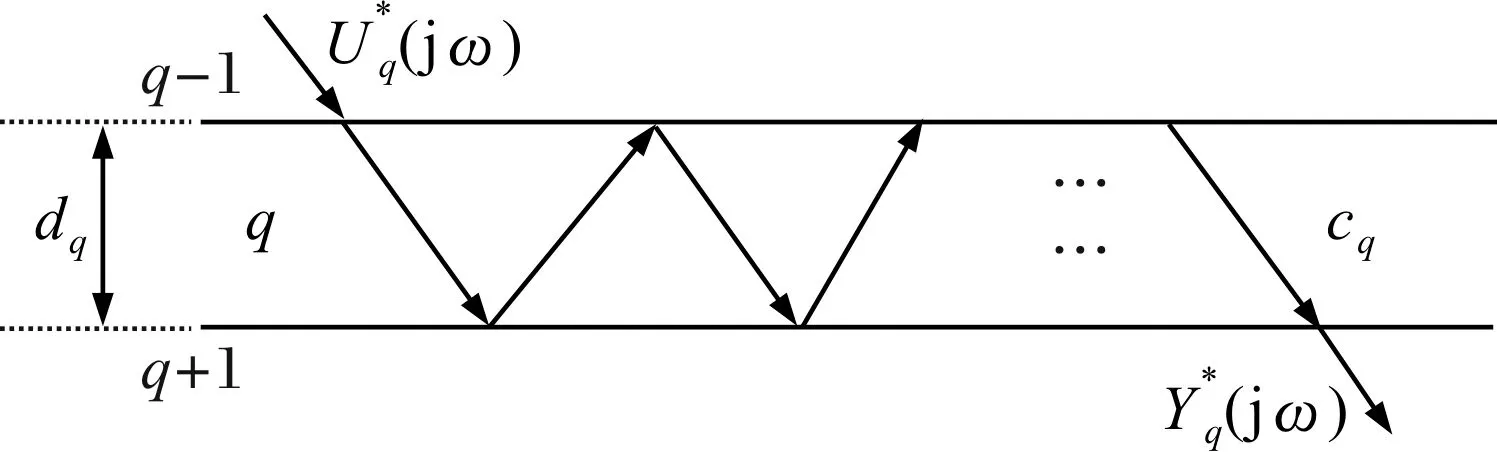
图5 信号从第(q-1)层下行到第q层，再下行到第(q+1)层传播示意图

信号从第(q-1)层入射到第q层，再透射到第(q+1)层的总信号为：

(12)

对应的传递函数为：

(13)

3)信号从第(q+1)层上行入射到第q层，经多次反射，从第q层上行透射到第(q-1)层。

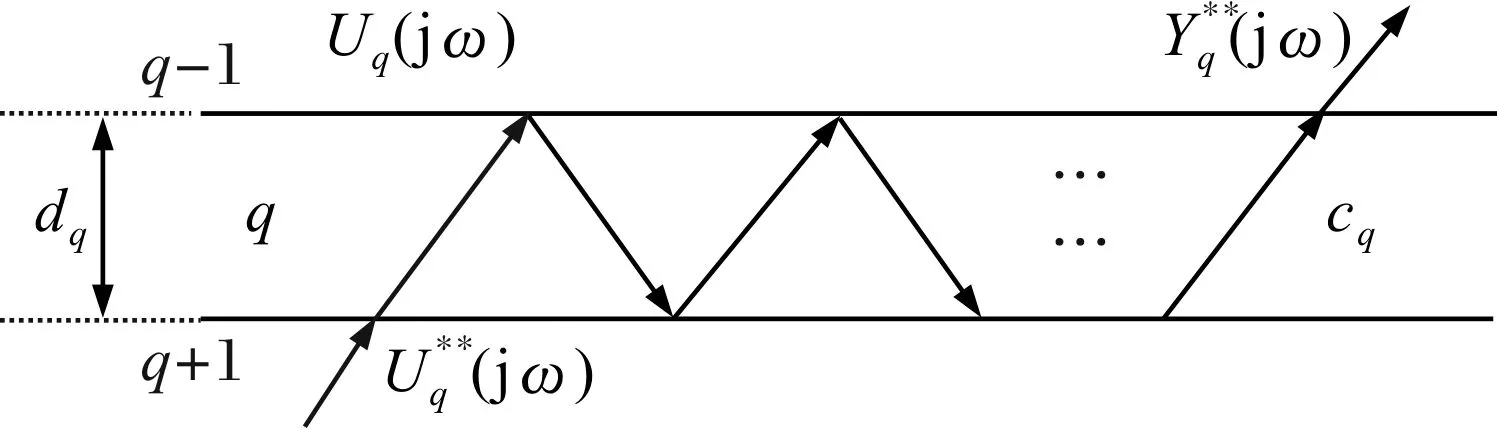
图6 信号从第(q+1)层上行到第q层，再上行到第(q-1)层传播示意图

信号从第(q+1)层入射到第q层，再透射到第(q-1)层的总信号为：

(14)

对应的传递函数为：

(15)

2 多层结构界面脱粘幅频特性和相频特性

固体火箭发动机多层结构模型如图7所示，图中虚线表示橡胶层不同的厚度,各层材料参数见表1[3]，各层材料不考虑声衰减。主要利用传递函数模型来研究多层结构1界面脱粘和2界面脱粘的幅频特性和相频特性，其中2界面脱粘的深度逐渐增大，如图7中的虚线变化。其中,d1=3 mm。

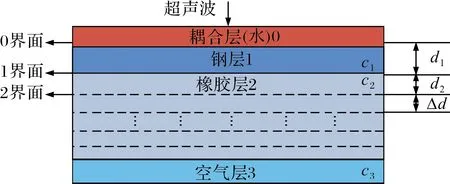
图7 多层结构示意图

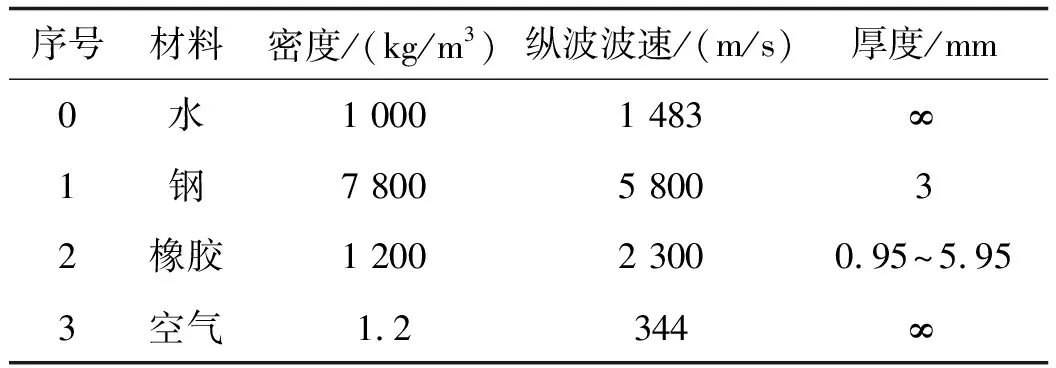
表1 多层结构的材料参数

当1界面脱粘时，假设耦合介质很薄，则其传递函数为：

(16)

当2界面脱粘时，其传递函数为：

(17)

式(16)～式(17)中，不同的透射系数T和反射系数R可由材料声阻抗求解[4]。

2.1 幅频特性变化

图8为多层结构界面脱粘幅频特性图，可以观察到1界面脱粘幅频明显不同2界面脱粘的幅频特性。对于2界面脱粘，文中其深度d2从0.95 mm开始以Δd为0.5 mm的厚度增加到5.95 mm。从图8中可以看出，随着2界面脱粘深度的增大，其对应的幅频特性曲线也发生细微变化。

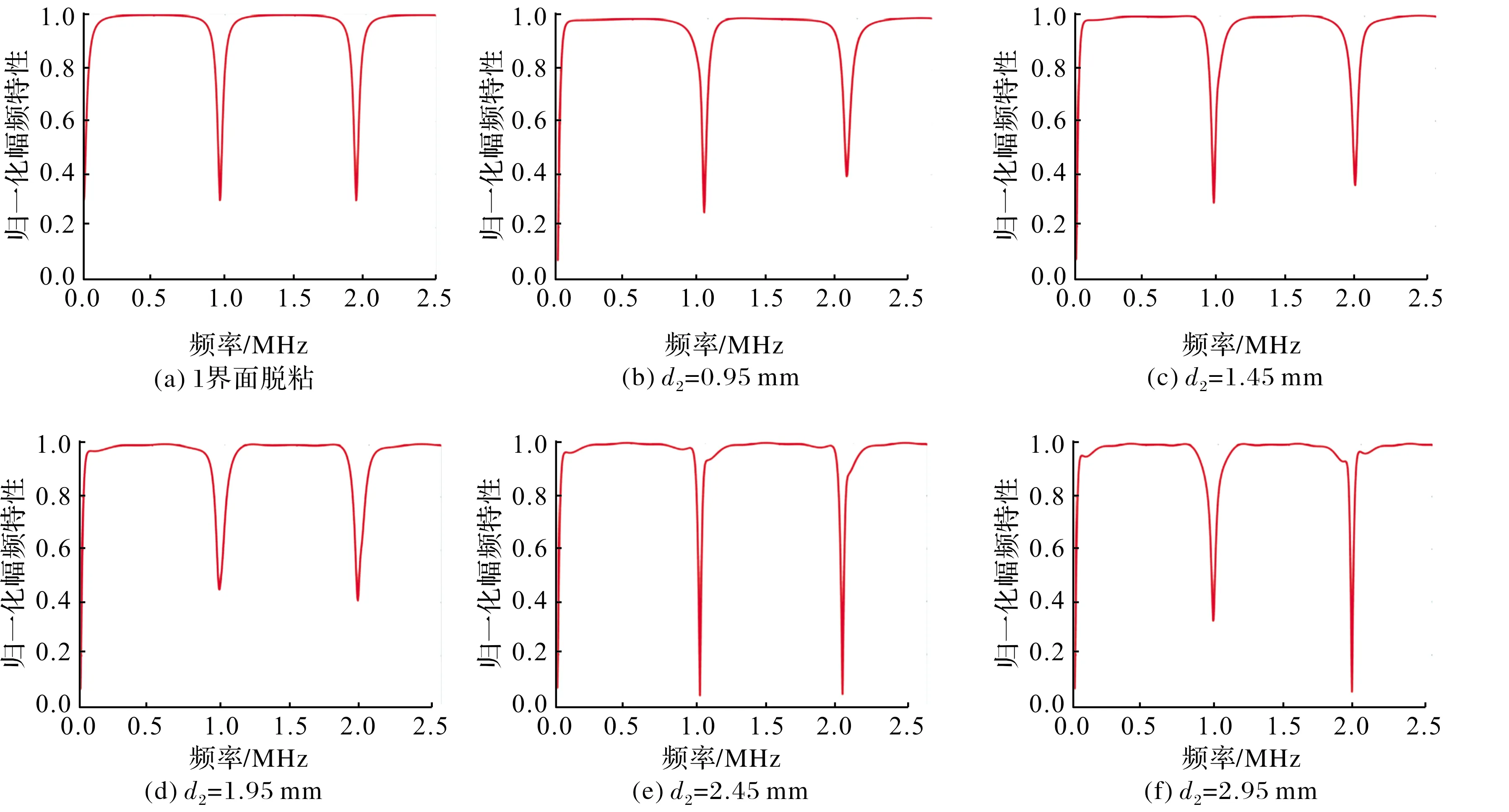
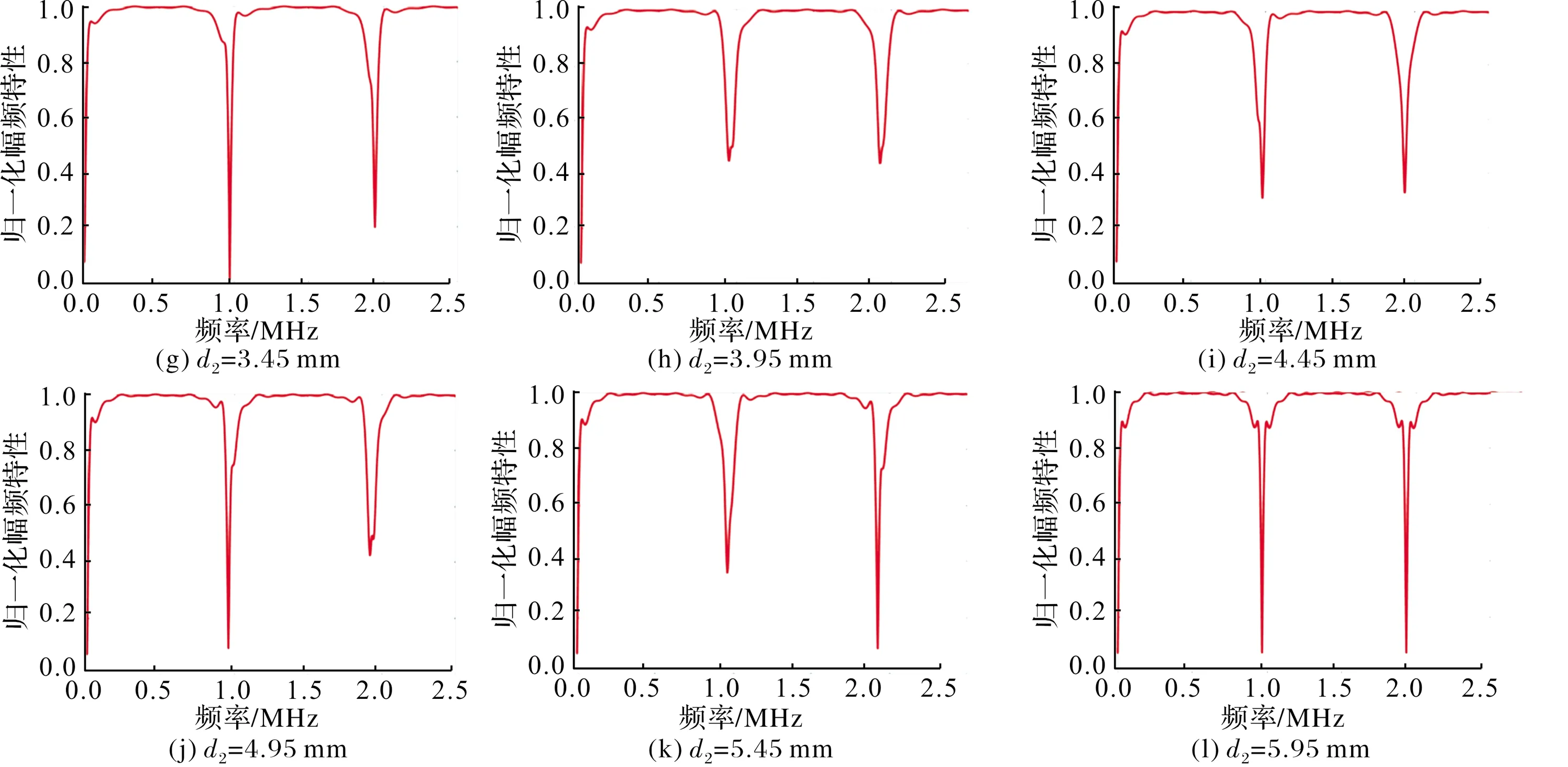
图8 1界面脱粘和2界面脱粘深度变化时的幅频特性

2.2 相频特性变化

图9为多层结构界面脱粘相频特性图，可以观察到1界面脱粘相频特性明显不同2界面脱粘的相频特性。随着2界面脱粘深度的增大，其对应的相频特性曲线也发生一定程度的变化。

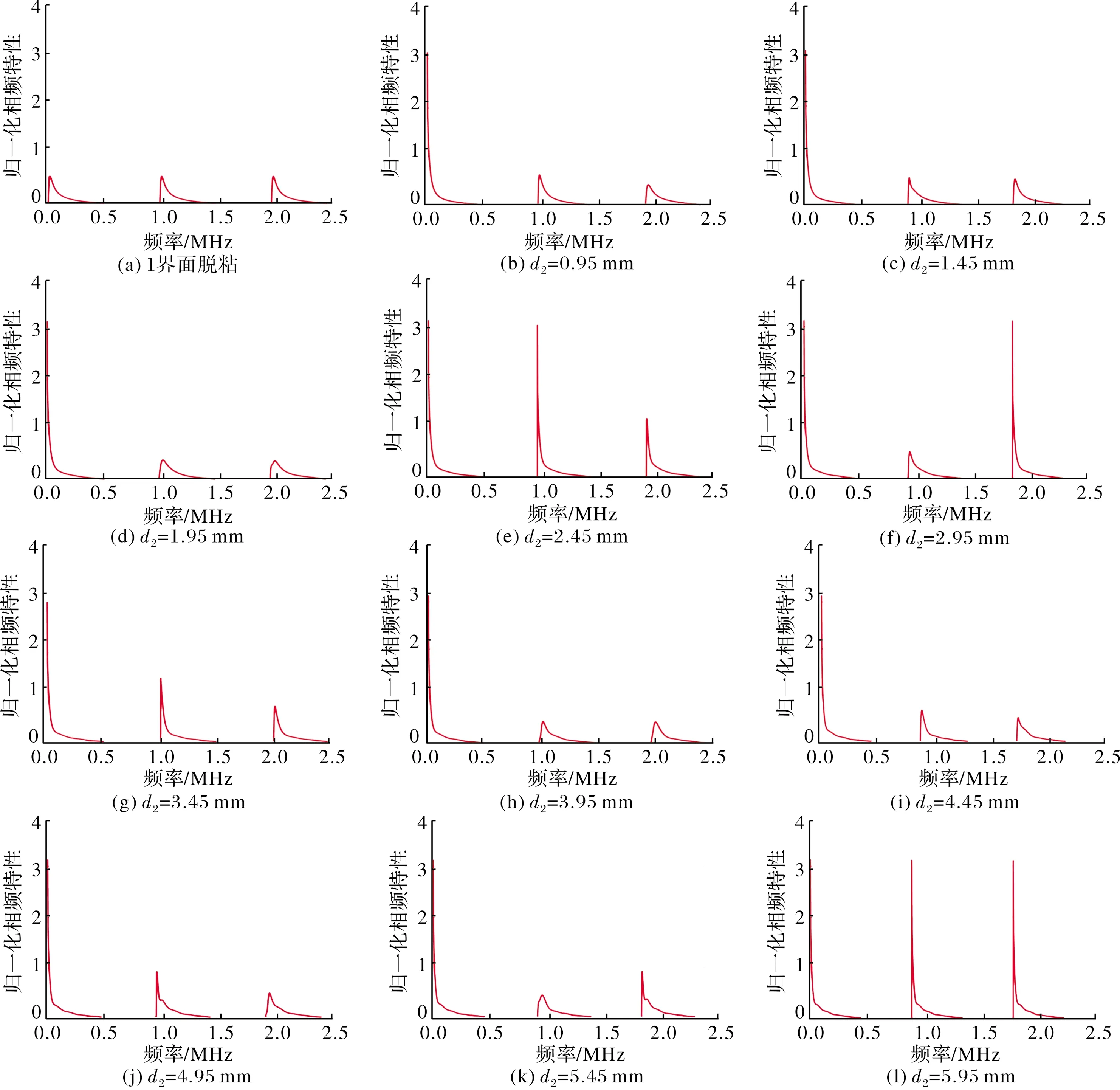
图9 1界面脱粘和2界面脱粘深度变化时的相频特性

3 结论

从信号传输的角度，建立了固体火箭发动机多层结构的数学模型，研究了多层结构脱粘时其幅频特性和相频特性的变化特点，主要结论如下：

1)多层结构1界面的脱粘，可通过其传递函数的幅频特性和相频特性来表征。

2)多层结构2界面脱粘深度的增大，其传递函数的幅频特性和相频特性也会发生相应的变化。

该研究为后续多层结构超声信号的分析与处理提供了理论基础,后续研究应该考虑材料对超声传播的衰减因素。