基于VMD变分模态分解的冲击波信号时频分析

郭佳辉，高一轩，刘昌伟，祖旭东

(南京理工大学机械工程学院，南京 210094)

0 引言

爆炸冲击波是战斗部毁伤效能评估的重要指标之一。大量的研究表明，爆炸冲击波作用时的毁伤效能，并非总是与超压峰值、正压作用时间成正比，其毁伤效能还与爆炸冲击波的频率特性有关。目前针对冲击波时域特征的分析较多，而对其频率特性的研究较少。因此，开展爆炸冲击波信号从时域分析到时频分析的探讨对爆炸冲击波毁伤效应的研究和工程防护的发展具有重要意义。

爆炸冲击波信号上升沿陡峭、突变快、持续时间短、包含多种噪声干扰，是典型的瞬态非平稳信号。通常采用小波变换、经验模态分解(EMD)和变分模态分解(VMD)等方法对其进行时频分析。小波变换由于其窗函数可变，具有良好的时频局部化特性，被广泛应用于信号分析中。李丽萍等通过基于小波包的改进HHT(希尔伯特-黄变换)方法，马伦等结合Morlet小波采用尺度相关能量分布确定尺度参数的方法，提高了信号分解计算的精度。但上述研究由于窗函数的选取在整个分析过程中无法更换，所以小波变换缺乏对信号处理的自适应性。EMD方法可以实现对信号的自适应滤波，但这种递归模式分解方法存在一些问题，特别是各个模态之间存在不同程度的模态混叠与端点效应。VMD是一种新的非递归、变分模态分解估计方法。该方法利用交替方向乘子法(ADMM)迭代搜索变分模型最优解，令每个模态的估计带宽之和最小，实现信号的自适应分解，解决了EMD和LMD在递归模式分解过程中的模态混叠、对频率相近的分量无法正确分离、受采样频率影响等缺点，且时频分辨率强，噪声鲁棒性高。

文中从VMD算法的原理出发，探讨该方法在爆炸冲击波分解领域的适用性。依据实测爆炸冲击波信号的时频特征对算法中分解级数和惩罚因子的取值方法进行讨论，给出同时保持时域保真度和频域分辨率的爆炸冲击波信号分解方法；分析信号各级分量的时频特性，得到冲击波能量的时频分布规律。

1 VMD算法原理

VMD是2014年由Dragomiretskiy等提出的一种信号处理方法。其分解过程可以概括为将原始信号通过筛选，将频率占优信号分解为调幅调频信号的集合。假设每个“模态”的有限带宽有中心频率，使每个模态的估计带宽的和最小，实现信号的自适应分解，约束条件为各模态之和等于输入信号。固有模态函数(IMF)，即是通过幅频调制的谐波信号。

阶IMF分量可以表示为：

()=()cos(())

(1)

式中：()为()的瞬时幅值；()为()的瞬时频率；()是一组离散的子信号，在时频谱中每个子信号的带宽稀疏不同。

1.1 变分问题构造

由于VMD分解时具有一定的稀疏性，在进行阶分解时，为了获得IMF分量的带宽，可以将其看作约束变分问题。

VMD方法在评估IMF分量带宽时，首先对于每个IMF分量进行希尔伯特变换计算出相应的解析信号，以获得一个单边频谱；然后加入指数项调整各中心估计频率，将IMF分量的频谱移至“基带”上；最后利用调制信号进行高斯平滑估计带宽，如平方范数的梯度。约束变分模型表达式为：

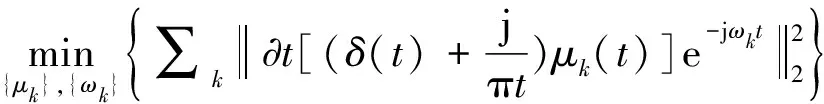
(2)

式中：为分解得到的IMF分量；为IMF分量的中心频率。

最优解约束条件为：

(3)

1.2 变分问题求解

为了求取上述约束变分问题的最优解，引入二次惩罚因子和拉格朗日乘子，则

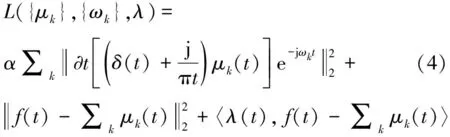
利用交替方向乘子算法求取上述增广Lagrange函数的鞍点，即为约束变分模型的最优解，从而将原始信号分解为个IMF分量。

(5)

(6)

利用傅里叶变换，将迭代后的结果转变到频域可得：

(7)

(8)

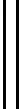
2 冲击波超压曲线测试试验

2.1 试验内容

为测试炸药在空气爆炸时不同特征点的超压时程曲线，设计了爆炸试验。采用自由场超压传感器，将30 g TNT爆炸后的爆炸冲击波压力信号转换成电信号，通过传输电缆将信号输入数据采集仪，由压力传感器的灵敏度和信号传输、记录的放大倍数，计算出冲击波超压时程，确定峰值超压。图1为冲击波超压试验的测试原理图，所用炸药的规格为30 g TNT圆柱装药(装药尺寸Φ25 mm×38 mm)，起爆方式为单端起爆；超压传感器为压电式，测量过程中感应面朝向爆心；传感器支架具备所需的刚度，并固定可靠；传输电缆有良好保护，测试时与动态测试仪连接。

图1 爆炸冲击波信号测试原理图

如图2所示，此次试验设置2个测点，分别距爆心300 mm和500 mm。试验过程中，2个测点错开布置，避免测试过程中仪器间的相互干扰。同时，为确保试验冲击波波形和峰值超压结果的可靠性，试验共重复3次，每次试验的布局完全相同。试验现场炸药布置和测点布置如图3所示。

图2 传感器测点布置图

图3 试验现场图

2.2 试验结果

通过试验得到30 g TNT空气中爆炸后在距离爆心300 mm和500 mm处的爆炸冲击波超压时程曲线，如图4所示。

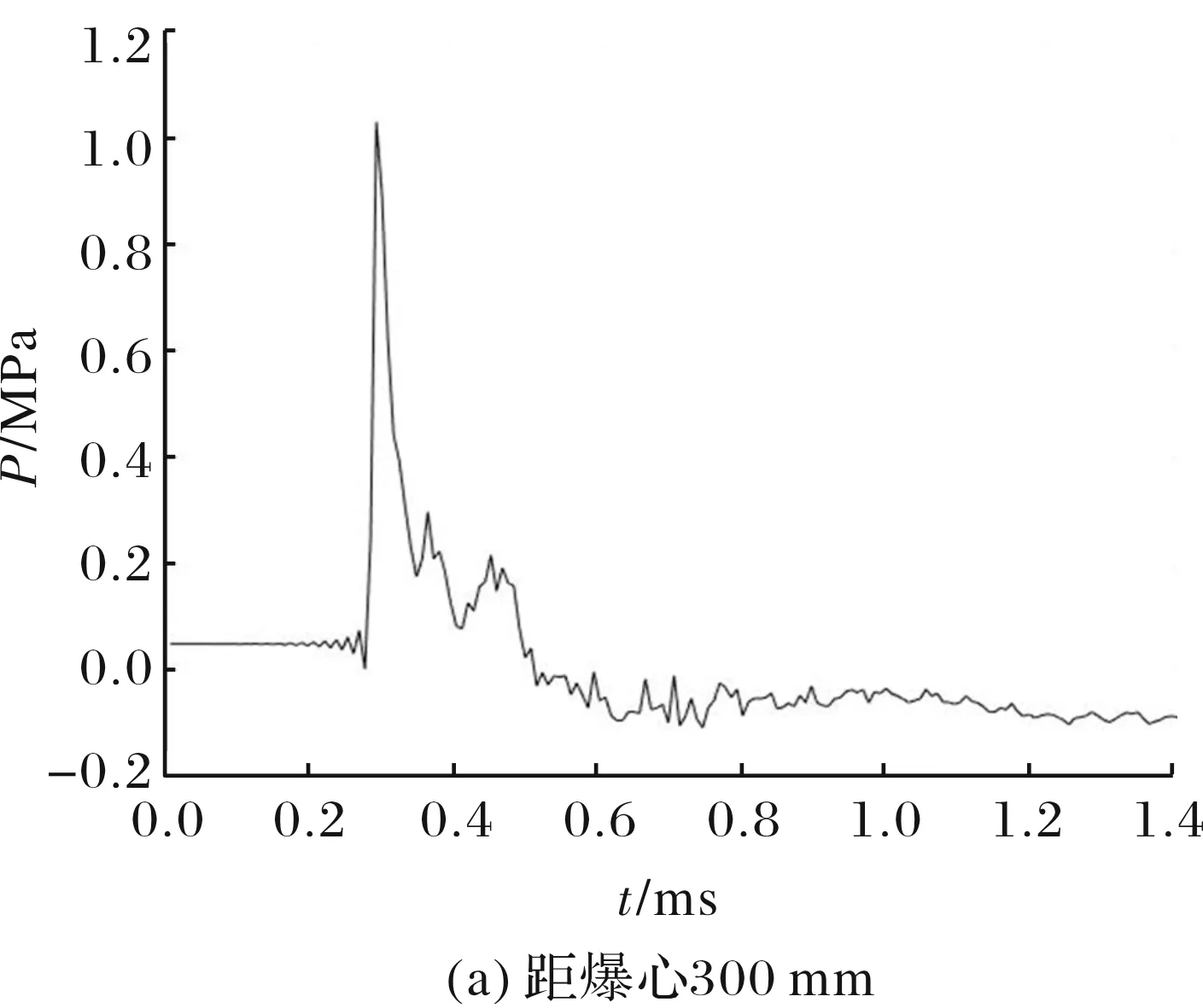
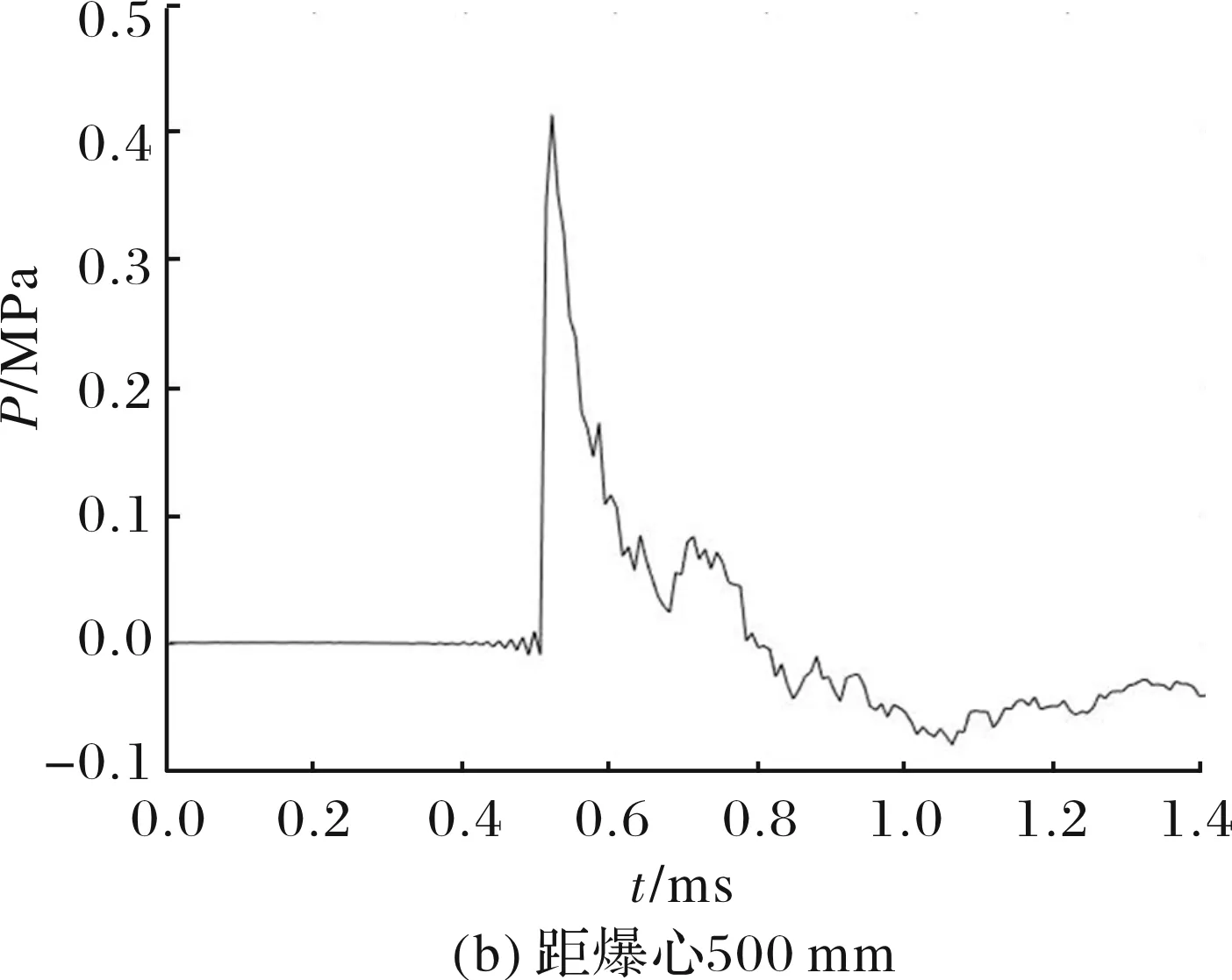
图4 冲击波超压时程曲线

3 冲击波信号VMD分解

3.1 VMD分解参数讨论

下面对图4(a)进行变分模态分解。VMD算法中的关键问题是需预设惩罚因子、模态分解级数、保真系数及收敛条件等参数。其中惩罚因子和模态分解级数对分解结果的影响最为显著。的取值会影响分解精度，其取值越低，各IMF分量的带宽越大；相反取值越高，IMF分量的带宽越小，甚至会使得程序进入死循环，无法得到结果。的取值直接影响分解结果，值太小导致信号分段不足，某些模态下的子信号会被当成噪声；值太大会捕获额外的噪声，出现模态混叠现象。由于爆炸冲击波信号复杂多变，和通常难以确定。如何选定合适的参数组合，是决定VMD方法在冲击波信号分解上适用性的关键所在。对此，相关学者通过排列熵法、样本熵法、遗传变异粒子群算法等对和的取值进行寻优，获得了较好的分析结果。含较大趋势项的爆破信号经过VMD算法分解后，得到的一阶IMF分量为信号趋势项，分解结果与的取值无关。然而，由于不确定原理的存在，时域和频域的精度无法同时保证，上述寻优方法的求解结果受适应度函数影响较大，经检验这些方法的适应度函数对爆炸冲击波这种频域较宽的短脉冲信号适应较差，不宜作为寻优标准。

综合前面的讨论，拟通过信号自身的时频特性来确定和的取值。如图5所示，首先将原始冲击波时域信号通过傅里叶变换得到其频谱图，然后依据冲击波信号的频谱特征将冲击波信号频谱图分为4段，可近似认为信号主要由4个频率带组成，因此，取模态分解级数=4。

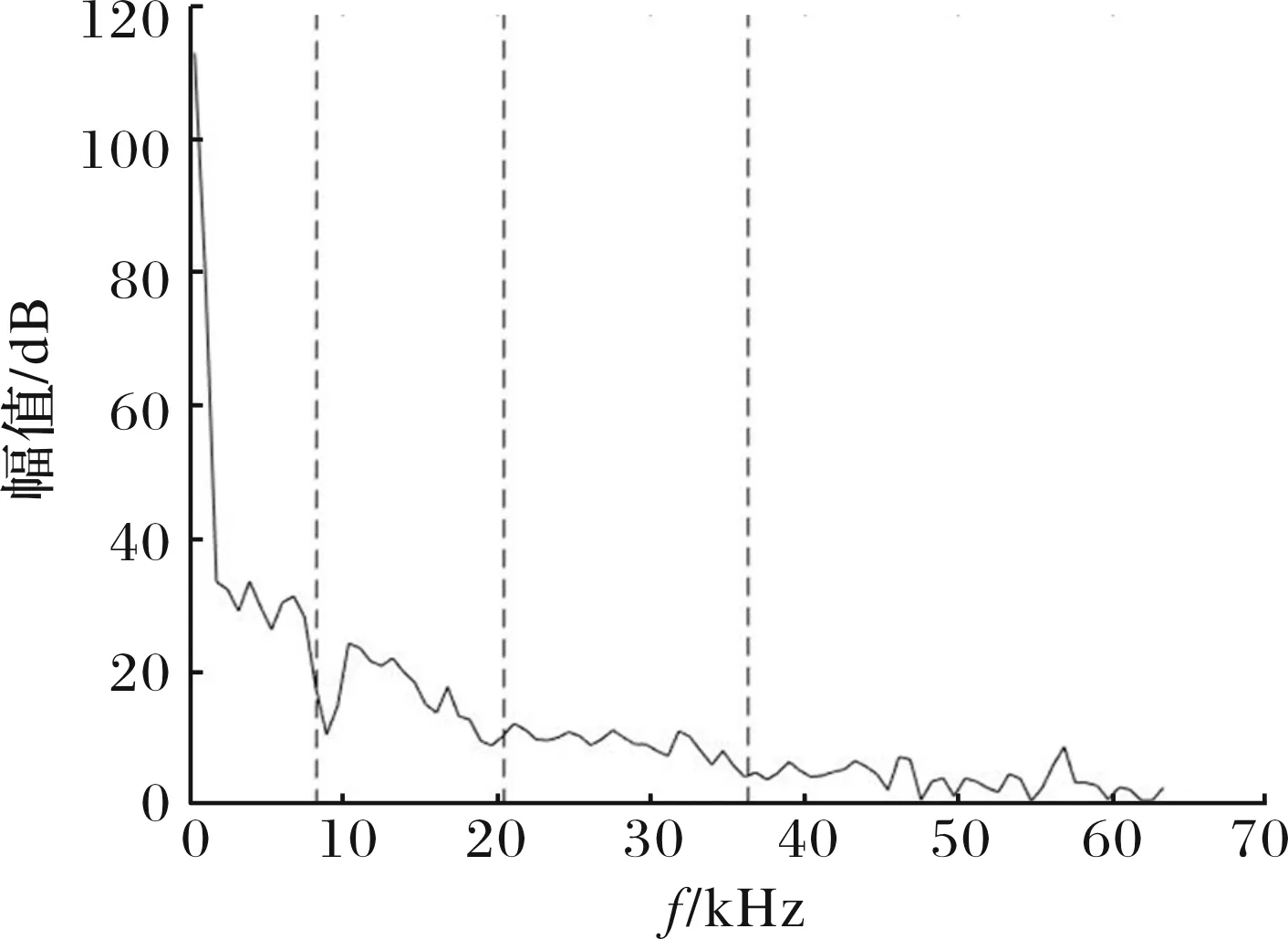
图5 冲击波信号频谱图

惩罚因子主要影响IMF分量的收敛速度，其取值与信号的长度有关，多数情况下，将设置为2倍的输入信号长度，即=2。然而，经尝试发现重构后的时域信号会出现严重的失真和端点效应，频域分辨率较高，但会出现部分高频信号的缺失，见图6。

图6 α=2N时分解曲线

当≤0.1时，重构信号的时域保真度较高，但频域的低频部分出现模态混叠，见图7。

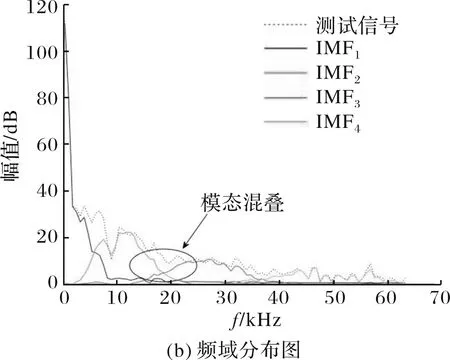
图7 α=0.1N时分解曲线

综合以上讨论，的取值应在同时保证时域保真度和频域分辨率之间进行平衡。经过尝试发现在015～05范围内取值时，重构信号时域失真较小且频域分辨率较高，是较为理想的分解结果，见图8。

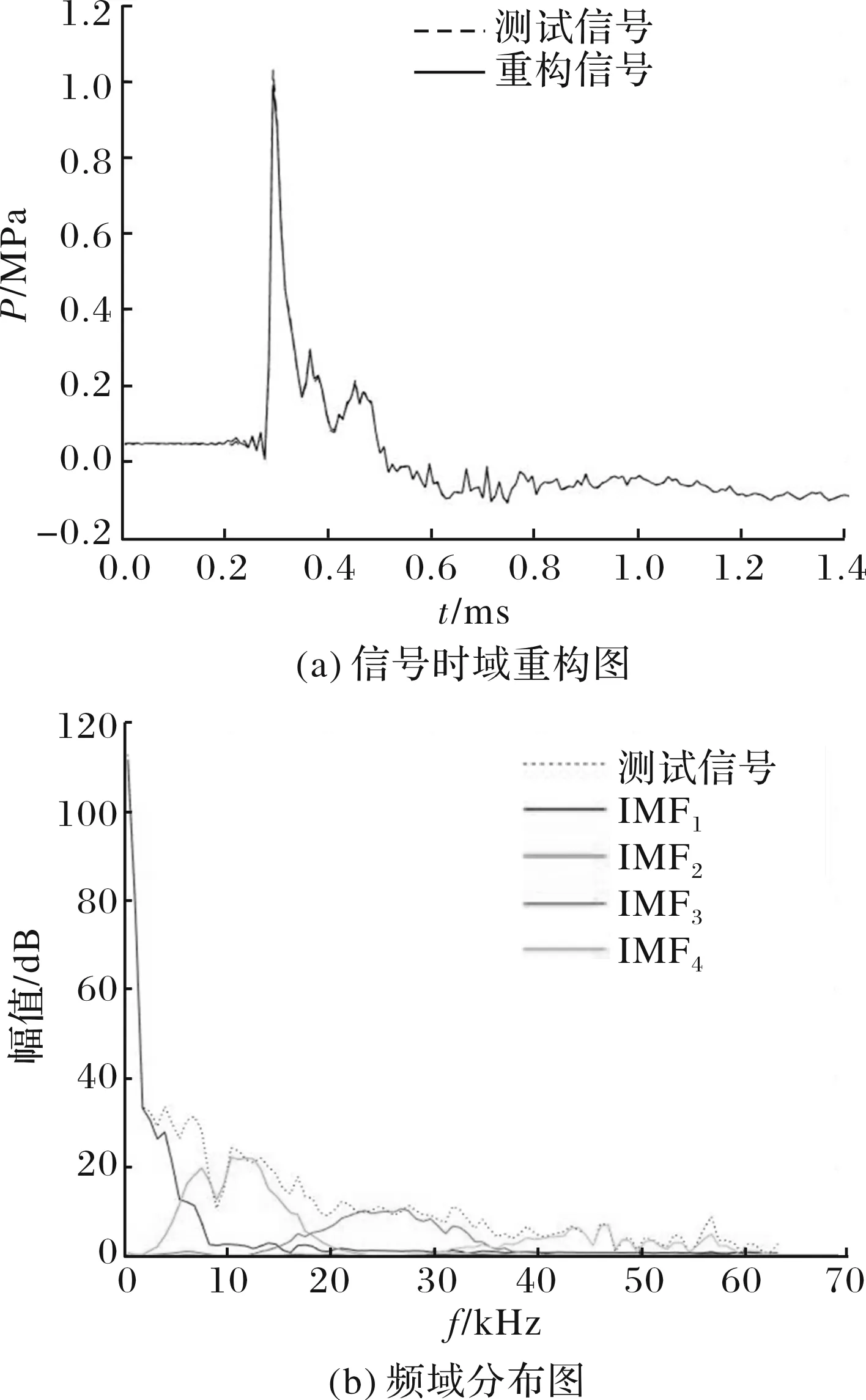
图8 α=0.3N分解曲线

3.2 VMD结果分析

取=4，=0.3对爆炸冲击波信号进行VMD分解，分解后得到4个基本IMF分量。各分量的时域和频域对照图见图9。

可以看出爆炸冲击波信号的频谱范围很宽，所含频率成分较多。随着IMF分量的分解级数增加(由IMF至IMF)，其时域幅值减小，持续时间增加。其频域幅值减小，频谱带宽增加。频域的幅值幅度变化程度较时域更大。

VMD分解所得到的IMF分量具有物理意义。其中IMF分量为实测冲击波信号的优势子频带，IMF、IMF分量为信号的中低频部分，IMF分量为信号的高频部分。爆炸冲击波能量主要集中在中低频部分和优势子频带部分，而在高频部分噪声能量占比较大，冲击波的能量分布相对较少。在低频部分的IMF分量幅值较大，频带较窄，在高频部分的IMF分量幅值较小，频带较宽。

图9 各级IMF分量的时域和频域对照图

4 结论

对爆炸冲击波信号进行了变分模态分解，通过对分解结果的处理和分析，得到以下结论：

1)变分模态分解算法在爆炸冲击波信号时频分析方面适用性较好，当惩罚因子取0.15～0.5倍信号长度，且分解级数取幅频曲线分段数时，可以获得重构信号失真小、频率分辨率高的分解结果。

2)采用VMD方法对冲击波信号进行分解可以得到各分量的时域波形和各频率分量的分布范围,为爆炸冲击波时频分析提供了一种新思路。

3)爆炸冲击波所含频率成分较多，频谱范围较宽,其中冲击波的能量主要集中在中低频段幅值大频带较窄，高频分量幅值小频带较宽。