基于LESO的制导火箭鲁棒滚转控制设计

杨 靖，杜凤怀，高晓波，娄 江

(西安现代控制技术研究所，西安 710065)

0 引言

制导火箭武器系统因其反应迅速、火力猛、威力大、成本适中等优点，自第二次世界大战以来一直是世界各国竞相发展的骨干装备。武器装备的发展一直是基于作战理念，服务于作战任务。近年来，随着“精确、立体、跨域、多能”作战理念的发展，对制导火箭遂行任务能力提出了新的挑战。三通道控制滚转角稳定是提升制导火箭机动性、扩展其任务能力的重要途径之一。

大空域、宽速度范围的制导火箭，其滚转控制具有快时变、非线性、高不确定性和强干扰等特点。近期，在某小口径制导火箭的飞行试验中，观测到滚转角响应较长时间内脱离滚转指令而滚转舵偏又很小，如图1所示。究其原因在于：小口径、小展弦比翼结构布局弹体，其刚体动力学模型小扰动线性化后，滚转通道传递函数增益较高且范围较宽，导致采用传统的增益调度PID 控制时，参数取值较小，系统的鲁棒性及抗干扰能力差。

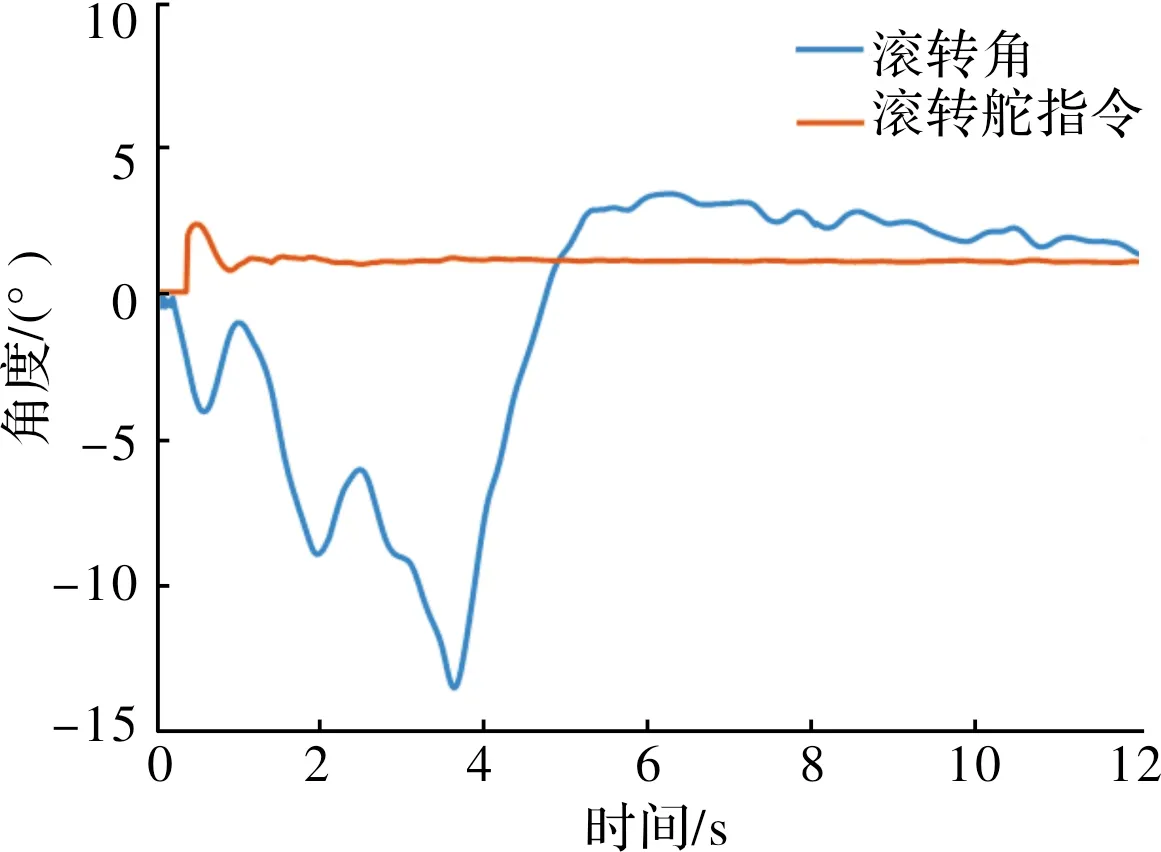
图1 滚转角和滚转舵指令随时间的变化曲线

目前，国内外针对制导弹药滚转鲁棒控制研究多采用非线性控制方法，包括滑模控制、自适应控制等，能够抑制模型不确定性和扰动，稳定快速收敛到平衡点，但是难以从理论上确定其裕度和对应离散系统的性能。对于多通道多回路复杂弹体，执行机构带宽及最大偏转角、弹载计算机计算周期等受到限制，为达到满意的效果，需要进行反复迭代和大量的仿真验证。

线性扩展状态观测器能够重构系统状态和估计扰动，且频域特性清晰，便于工程实现。因此，文中提出了一种基于线性扩展状态观测器的鲁棒滚转角控制方法。通过线性扩展状态观测器，对被控对象的建模误差、内部和外部扰动进行实时估计并动态补偿。综合考虑舵机环节和线性扩展状态观测器的迟滞效应，在扰动补偿回路中增加校正网络，提高稳定裕度。仿真表明，该方法可有效抑制滚转扰动力矩的影响，提高了滚转控制的鲁棒性。

1 数学模型

1.1 弹体滚转通道模型

基于小扰动线性化，将通道耦合等视作干扰项，轴对称制导火箭滚转动力学模型可简化为：

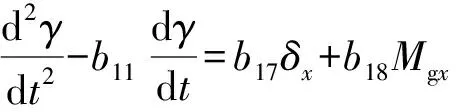
(1)

式中:为滚转角;为滚转舵偏角;g为滚转干扰力矩;为空气动力阻尼系数;为操纵系数;为干扰力矩传递系数。

经拉氏变换，滚转舵偏角到滚转角和滚转角速度的传递函数可表示为:

(2)

式中:为滚转角速度;=-为弹体增益;=-1为时间常数。

1.2 电动舵机模型

伺服电动舵机特性，用二阶动力学环节来近似，可表示为:

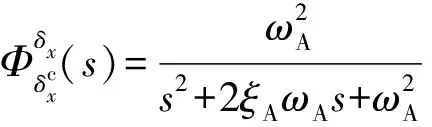
(3)

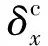
2 基于LESO的滚转控制设计

2.1 线性扩展状态观测器

考虑阶单输入单输出不确定系统:

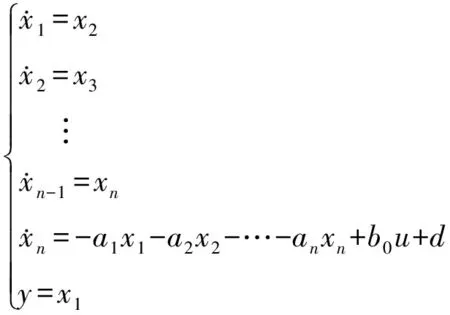
(4)

式中:为系统状态变量,=1,2,…,;和为系统参数的已知最佳估计,=1,2,…,;为测量输出;为控制输入;包含未建模误差和未知扰动。

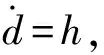
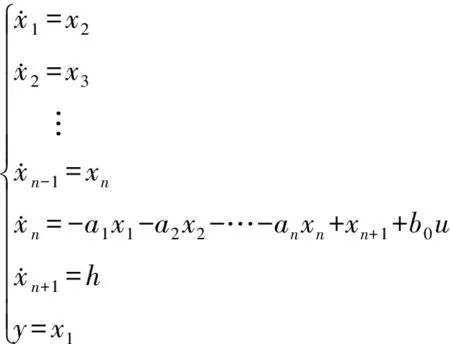
(5)

式(5)增广系统的+1阶线性状态观测器结构为:

(6)

式中:为观测器增益,=1,2,…,+1。可以看出，观测器的输入为原系统的控制量和输出量，结构参数仅用到原系统控制输入传递系数。

2.2 基于LESO的滚转控制器

对于仅滚转角速度可测量的情形，传统的滚转自动驾驶仪通常采用PI+测速反馈控制，其框图如图2所示。当要求滚转角稳定到常值时，相当于PID控制。为利用PID控制的优势，文中首先采用线性状态观测器对扰动进行估计并加以动态补偿，然后综合考虑舵机环节和线性状态观测器频率特性，设计PID控制参数，改善幅值和相位裕度，其框图如图3所示。

图2 “PI+测速反馈”滚转自动驾驶仪框图

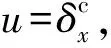
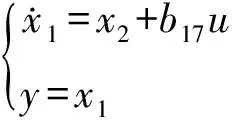
(7)

对式(7)表示的系统，建立二阶线性扩展状态观测器，即

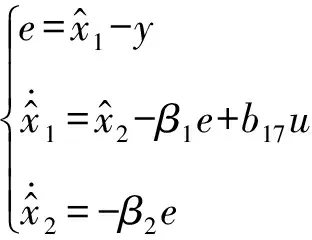
(8)

(9)

图3 基于LESO的“PI+测速反馈”滚转控制框图

动态补偿回路闭环传递函数为:

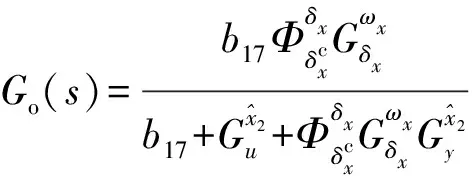
(10)

将动态补偿后的回路作为新的被控对象，采用PID校正网络，进行频域设计，将截止频率调整到合适值，提高稳定裕度，以满足滚转动态性能要求。

3 数值仿真

以某型制导火箭为例，特征点弹体参数和舵机参数如表1所示。分别采用传统的“PI+测速反馈”和基于LESO的“PI+测速反馈”两种控制方法进行滚转角稳定自动驾驶仪设计。通过数值仿真，对比有无干扰情况下，传统的“PI+测速反馈”和基于LESO的“PI+测速反馈”两种控制方法的控制效果。最后，对该型制导火箭进行全弹道仿真，检证所提出方法的应用效果。

表1 弹体和舵机参数

3.1 传统的PI+测速反馈控制器

对表1所列参数，按照图2所示控制框图，取控制参数=0.0581，=0.0100，=0.0032,系统开环截止频率为3.8 Hz，相位裕度为45°，幅值裕度17.1 dB，如图4所示。

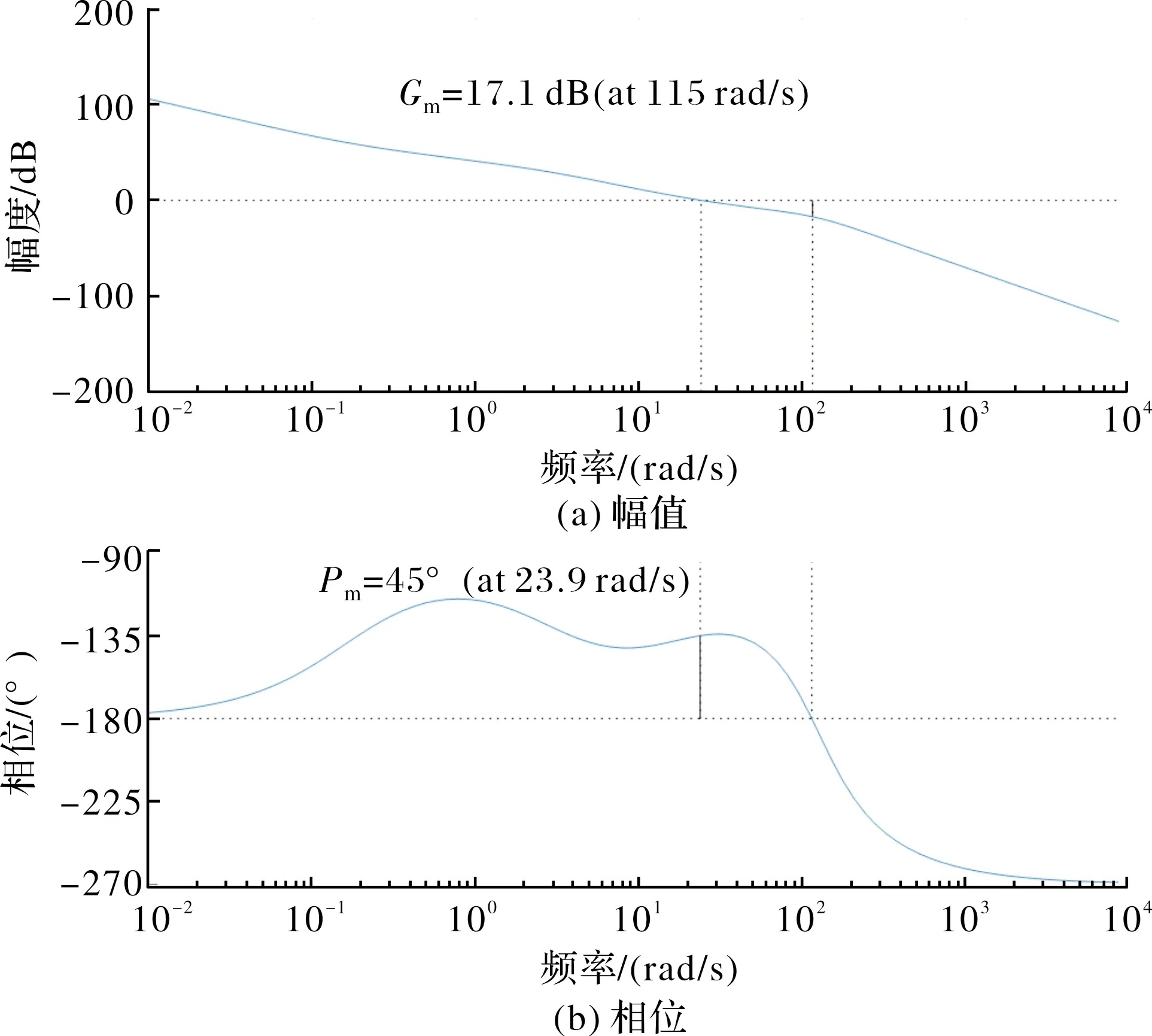
图4 传统“PI+测速反馈”控制幅值和相位裕度

3.2 基于LESO的PI+测速反馈控制器

对表1所列参数，采用图3所示控制框图，取参数=73，=1772，则扩展状态观测器带宽为15.2 Hz；取控制参数=0.0407，=0.0022，=0，系统开环截止频率为3.0 Hz，相位裕度为44.2°，幅值裕度为18.5 dB，如图5所示。

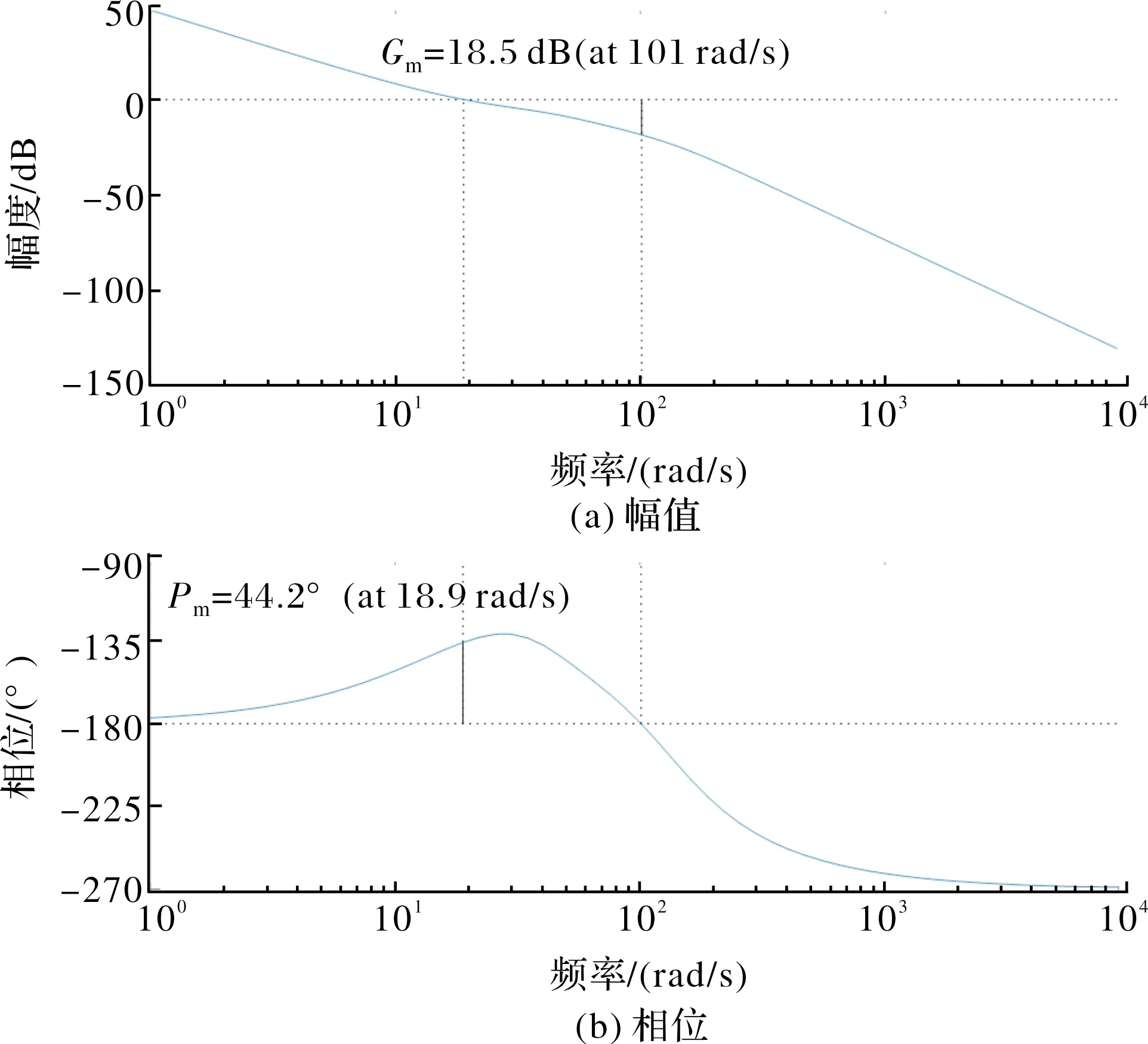
图5 基于LESO的“PI+测速反馈”控制：幅值和相位裕度

3.3 两种方法性能对比

图6给出了在特征点单点仿真中两种方法的效果。滚转角指令为0.5 s开始的单位阶跃指令，在1.5 s时加入等效舵偏角为-1°的扰动力矩。可以看出，幅值和相位裕度相当的两种方法，传统的“PI+测速反馈”控制结果表现为滚转角响应长时间脱离滚转指令，而基于LESO的控制方法在扰动情况下，快速收敛到滚转角指令。图7给出了两种方法对于该型制导火箭上升段的滚转控制仿真结果，可以看出，基于LESO的控制方法具有较强的鲁棒性。

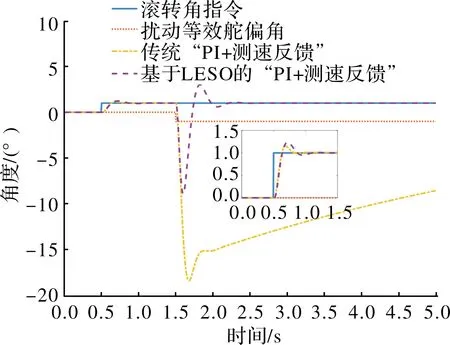
图6 两种方法对比(特征点单点仿真)

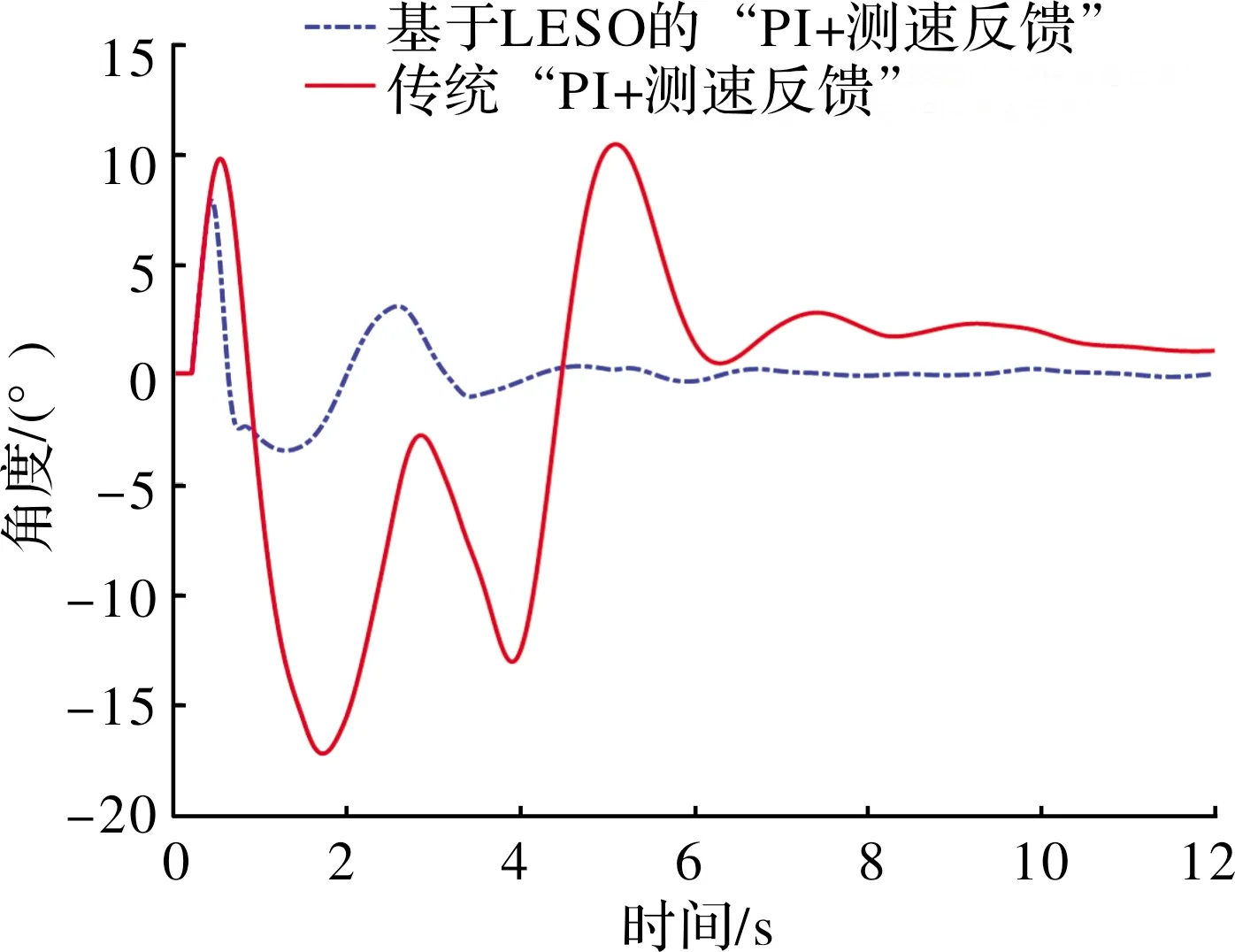
图7 两种方法对比(某型制导火箭上升段仿真)

3.4 延时对基于LESO的滚转控制的影响

针对实际应用中导航装置和弹载计算机的离散系统本质，主要分析图3所示控制框图中的两种延时情况：

情形1滚转角速度测量值(即输出)的延迟，在观测器用到的舵偏角指令(即输入)前加入相同的纯延时；

情形2输出存在延迟，且其与输入存在时差。

图8给出了对应情形1，输入与输出同时滞后不同时间，基于LESO的滚转控制方法在特征点单点仿真的结果。其滚转角指令为0.5 s开始的单位阶跃指令，在1.5 s时加入等效舵偏角为-1°的扰动力矩。可以看出，随着延时增加，单位阶跃响应的超调量增大，调整时间变长。当延时达到20 ms时，超调量增大到72.6%，调整时间增长至0.66 s，但是对扰动的抑制效果仍较好。当延时达到30 ms时，出现明显的振荡，但系统仍然是稳定的。

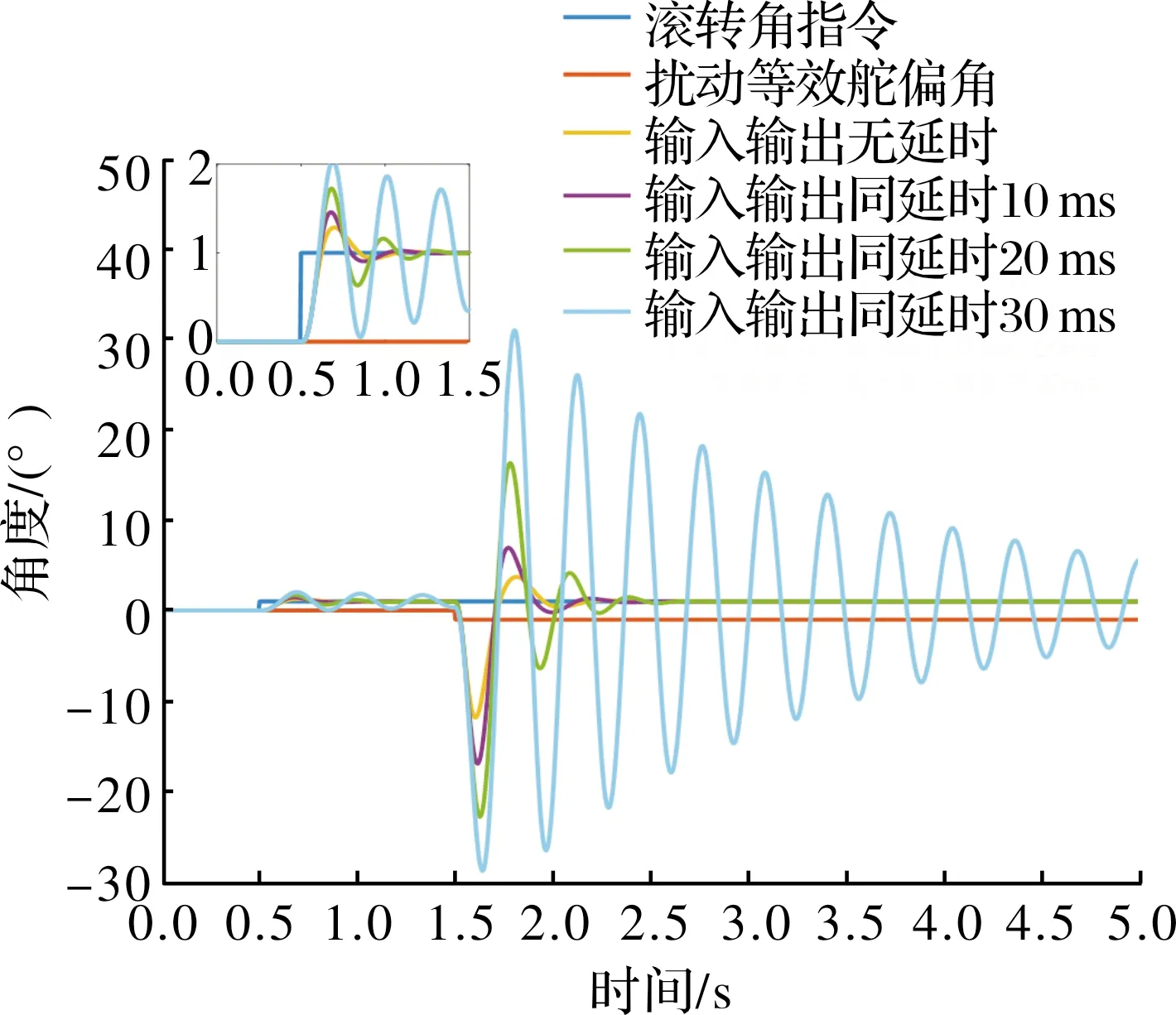
图8 输入输出相同延时对基于LESO的滚转控制的影响

图9给出了对应情形2，输入无延时，输出分别滞后5 ms、10 ms、15 ms，基于LESO的滚转控制方法在特征点单点仿真的结果。其滚转角指令为0.5 s开始的单位阶跃指令，在1.5 s时加入等效舵偏角为-1°的扰动力矩。可以看出，随着输入输出时差增加，单位阶跃响应的超调量增大，调整时间变长。当延时差为10 ms时，超调量增大到44.7%，调整时间增长至0.56 s，但是对扰动的抑制效果仍较好。当输入输出延时差达到15 ms时，系统振荡发散。因此，通过测试系统滚转角速度输出的实际延时，对观测器用到的舵偏角指令输入先进行滞后处理是必要的。

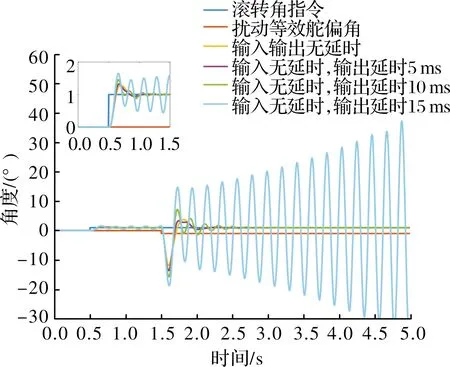
图9 输入输出时差对基于LESO的滚转控制的影响

4 结束语

针对跨域小口径制导火箭滚转角稳定设计中传统的PID控制方法抗干扰能力差的问题，提出了一种基于线性扩展状态观测器的鲁棒滚转角控制方法。对滚转角速度可测的情形，通过二阶线性扩展状态观测器，对被控对象的建模误差、内部和外部扰动进行实时估计并动态补偿。综合考虑舵机二阶动力学模型和线性扩展状态观测器的迟滞效应，在扰动补偿回路中增加校正网络，提高稳定裕度。仿真结果表明，该方法对常值扰动具有良好的鲁棒性。值得注意的是，观测器用到的舵偏角指令和导航装置滚转角速度测量值的时间差对系统性能影响较大，需要通过地面试验加以测量补偿。