青岛港口货物吞吐量预测应用研究

陈慧敏，孙晓燕，段晓亮，陈 虹

（1.北京经济管理职业学院，北京 100102；2.广西财经学院，南宁 530003）

一、引言

随着经济全球化趋势的加强，各个国家和地区之间的贸易来往也越来越密切，现代港口已经逐步发展成为经济贸易物流过程中的重要节点和贸易枢纽。港口物流供应能力的不足或过剩，都不利于物流业的健康发展，因此，对港口物流需求的准确预测，不仅能为制定港口物流系统规划提供指导性建议，而且对于促进我国物流业的全面发展具有不可或缺的作用。在预测模型方面，目前已经有非常丰富的理论成果和成熟的实践经验，主要的预测模型有时间序列模型预测算法、回归模型预测算法、灰色模型（Grey Model,GM）预测算法、BP（Back Propagation）神经网络预测算法等，这些预测模型和方法已经应用于各个领域。其中灰色GM（1,1）模型是预测模型中较为常用的模型，李楠基于单一灰色预测模型对北海港港口货物吞吐量进行了预测；徐伟通过对灰色预测和BP神经网络单一预测模型赋予权值，构成组合模型，提高了港口物流预测的精度。本文在现有研究成果的基础上，考虑到港口物流需求预测的非线性变化和我国物流实际数据统计不完善的情况，以青岛港为研究对象，根据港口的货物吞吐量数据构建GM(1,1)修正模型。首先，基于样本数据序列级比和可容覆盖范围θ，提出对模型数据进行线性平移的一次修正模型；然后根据一次修正模型的残差序列建立BP残差二次修正模型，进行残差预测；最后利用该残差预测值对一次修正模型的吞吐量预测值进行修正。通过实证分析，GM(1,1)修正模型的拟合值和预测值的平均相对误差有明显降低，在预测上具有更高的准确性，可以有效预测港口的货物吞吐量。

二、预测理论

（一）GM(1,1)模型

GM(1,1)表示模型是一阶微分方程，且只含一个变量的灰色模型。

定义1：已知样本数据序列x=（x(1)，x(2)，…x(n)），一次累加生成序列x=（x(1)，x(2)，…x(n)）=（x(1)，x(1)，x(2)，…，x(1)＋…＋x(n)），x的均值生成序列为z=（z(2)，z(3)，…z(n)），式中z(k)=0.5x(k)+0.5x(k-1)，k=2，3，…，n。

建立灰微分方程：

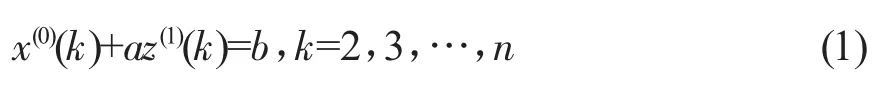
相应的GM(1,1)的白化微分方程为：

将方程(1)变形为：

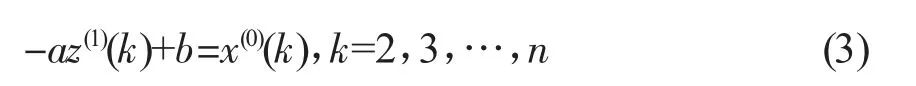
其中a，b为待定参数。

将方程(3)采用矩阵形式表达为：

即：Xβ=Y，其中

解方程(4)得到最小二乘解：

求解微分方程(2)，得到GM(1,1)模型的离散解为：

还原为原始序列，预测模型为：

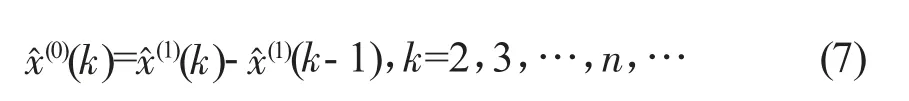
将式(6)代入式(7)得：

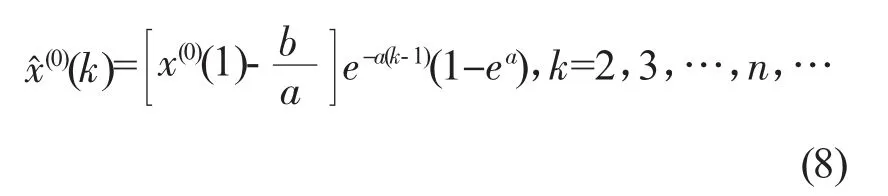
灰色GM(1,1)模型实际上是一种以数找数的方法，从系统的一个或几个离散数列中找出系统的变化关系，建立系统的连续变化模型，在数据处理和预测中经常使用。但是灰色GM(1,1)模型只适合指数增长数据的预测，而且该模型的使用往往因为其边界假设过多，存在对数据进行线型化处理的情况，导致预测结果与实际结果存在较大的差距。

（二）修正模型

考虑到GM(1,1)模型存在的上述问题，本文对模型进行两次修正：

1.一次修正

基于样本数据序列x的级比

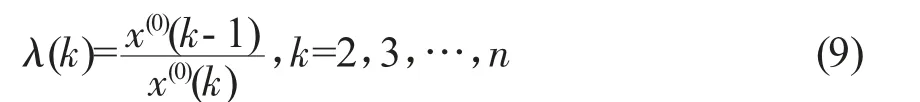
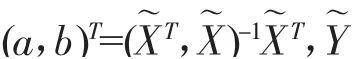
2.二次修正

第一步：基于一次修正模型，对样本数据序列x进行拟合，得到拟合值序列x～(k)，k=2，3，…，n，和预测值序列x～(k)，k=n+1，n+2，…；

第二步：计算得到残差序列ε(k)=x(k)-x～(k)，k=2，3，…，n；

第三步：建立样本数据序列x(k)，k=2，3，…，n和残差序列ε(k)，k=2，3，…，n的BP神经网络模型；

第五步：将新数据序列u作为BP神经网络的输入数据，进行残差序列预测，得到新的残差序列ε；

三、实证分析

（一）数据选取

为了验证修正模型在港口货物吞吐量预测中的有效性，选取2000-2019年青岛港口货物吞吐量数据进行实证研究，数据来源于《2020年青岛统计年鉴》“15-1主要年份客货运输及港口吞吐量”（具体数据如表1所示）。

表1 2000-2019年青岛港口货物吞吐量（万吨）

（二）GM(1,1)预测

以2000-2016年青岛港口货物吞吐量作为样本数据序列，通过构建的GM(1,1)模型，计算得到模型参数a=-9.24×10，b=1.2993×10，再根据预测模型式(8)，得到GM(1,1)模型的预测结果（其结果与实际值对比如图1所示；GM(1,1)模型的残差变化如图2所示）。

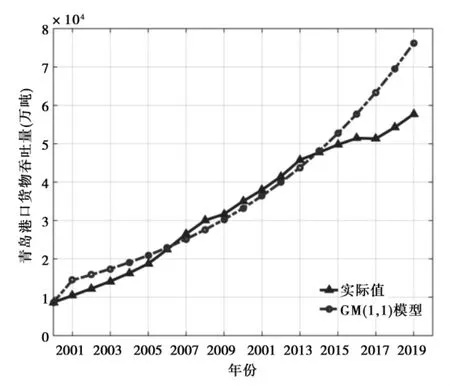
图1 GM(1,1)模型的预测结果及对比

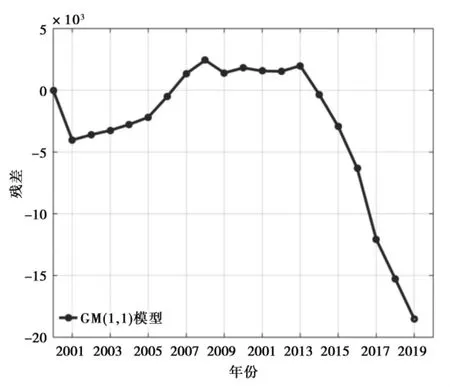
图2 GM(1,1)模型的残差变化

（三）一次修正模型预测

本次预测样本数据序列依旧选择2000-2016年青岛港口货物吞吐量，则该序列为x=（x(1)，x(2)，…x(n)）=（8661，10432，…51463），根据式（9）计算该序列的级比λ(k)，可知，该级比落在可容覆盖θ的范围之外，需要对x作平移变换，即：

式中常数c，可在一定的范围内进行选择，本次预测以级比λ(2)=0.999999进行计算，可得c=1.762×10，（变换后数据序列的级比如图3所示），其级比数值基本保持为一致，且均落在可容覆盖的范围内。

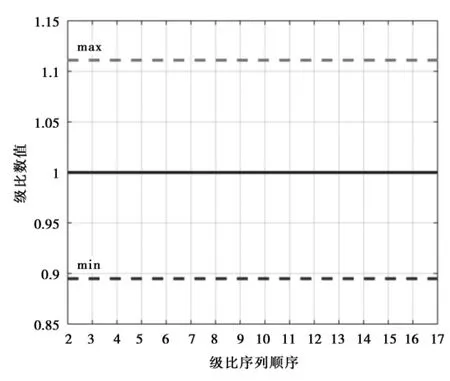
图3 变换后序列级比

根据一次修正预测模型，计算得到模型参数a=-1.6705×10，b=1.762×10；再根据预测模型式(10)，得到一次修正模型的预测结果（其结果与实际值以及GM(1,1)模型的预测结果对比如图4所示，模型的残差变化及对比如图5所示）。

图4 一次修正模型的预测结果及对比

图5 一次修正模型的残差变化及对比

（四）二次修正模型预测

根据二次修正模型的计算步骤，分别构建输入样本x和期望输出样本ε，采用三层BP神经网络结构，其隐含层的神经元选用S型函数tansig，输出层选用函数purelin，网络训练函数为trainlm，预设最大训练1000次，网络学习速率为0.05，目标误差值为1e-2，确定神经单元为5。从图6中可以看出，BP神经网络在学习次数达到不足100次时，学习曲线就开始收敛，趋于稳定。通过该BP神经网络模型，计算得到残差序列ε，并以此序列对一次修正模型再次进行修正，即二次修正模型。用二次修正模型进行预测并输出最终结果（其结果与实际值、GM(1,1)模型的预测结果和一次修正模型的预测结果对比如图7所示，模型的残差变化及对比如图8所示）。

图6 BP神经网络训练图

图7 二次修正模型的预测结果及对比

图8 二次修正模型的残差变化及对比

（五）结果分析

三种预测模型的预测结果与实际数据的对比如表2所示。从表2中可以看出，GM(1,1)模型的相对误差较大，尤其是平均预测误差达到了27.9%，但经过一次修正后，平均相对误差显著下降了；二次修正后，平均拟合相对误差仅为0.37%，平均预测相对误差仅为1.32%，预测精度得到了明显优化，预测值和实际值十分近似，表明经过二次修正后的模型是一种非常有效的预测模型。

表2 青岛港口2000-2019年实际值与修正模型模拟值的结果对比

四、结语

本文在灰色GM(1,1)模型的基础上，充分考虑样本数据的非线性及小样本特点，提出基于GM(1,1)模型的修正模型。并利用2000-2016年青岛港口货物吞吐量作为样本数据进行了实证分析，分别使用GM(1,1)模型、一次修正模型和二次修正模型对数据进行了拟合和预测。从拟合和预测结果的对比可以看出，经过二次修正后的GM(1,1)模型的拟合值和预测值与真实值的差距有明显改善，具有更高的准确性。结果表明，GM(1,1)修正模型用于港口的货物吞吐量预测是可行的。