输电工程管理中的微型桩杆塔基础有限元数值模拟
陈红发 吕鸿斌 霍历炜 李燕 白钰
(1.宁夏天净元光电力有限公司 宁夏回族自治区银川市 750004)
(2.国网宁夏电力经济技术研究院 宁夏回族自治区银川市 750004)
(3.国网银川供电公司 宁夏回族自治区银川市 750004)
微型桩是近年来逐渐发展起来的一种新型桩基础,又称树根桩。微型桩采用二次注浆,一般其直径小于400mm,长细比大于30,承载力较大[1]。其主要特点有施工机具小,适用于狭窄的施工作业区;施工振动、噪音小,且对土层适应性非常强[2]。
微型桩的概念最早于上个世纪50年代由意大利的Lizzi提出,1982年由法国Soletanche 公司将微型桩技术引入国内,引起国内学术界的广泛重视[3]。在国内主要应用于古建筑加固纠偏、房屋和防洪堤坝加固、边坡加固、旧房改造、建筑物加固防震抵抗交替荷载的基础、水池底板的抗浮等工程。近年来,微型桩逐渐在杆塔基础中得到应用,龚健等在软土地基中进行大量微型桩单桩和群桩现场原型试验,结果表明微型桩基础在软土地基杆塔基础中的应用具有足够的安全性能[4]。苏荣臻等对黄土地基微型桩杆塔基础施工工艺进行了现场原型试验[5],郑卫锋等在青海地区进行了微型桩现场试验,针对寒冷地区施工问题进行了分析[6]。除此之外,中国电力科学研究院与各相关单位协同工作,先后在上海、天津等地进一步试点研究并获得了较好的经济和社会效益。
运用Abaqus 程序对单桩进行了抗压、水平力的数值计算分析,研究了微型桩的受力特性和工作特性,以期对微型桩基础的设计计算进行优化,进一步推进微型桩基础在输电线路中的应用。
1 微型桩应用中存在的主要问题
1.1 问题现状及分析
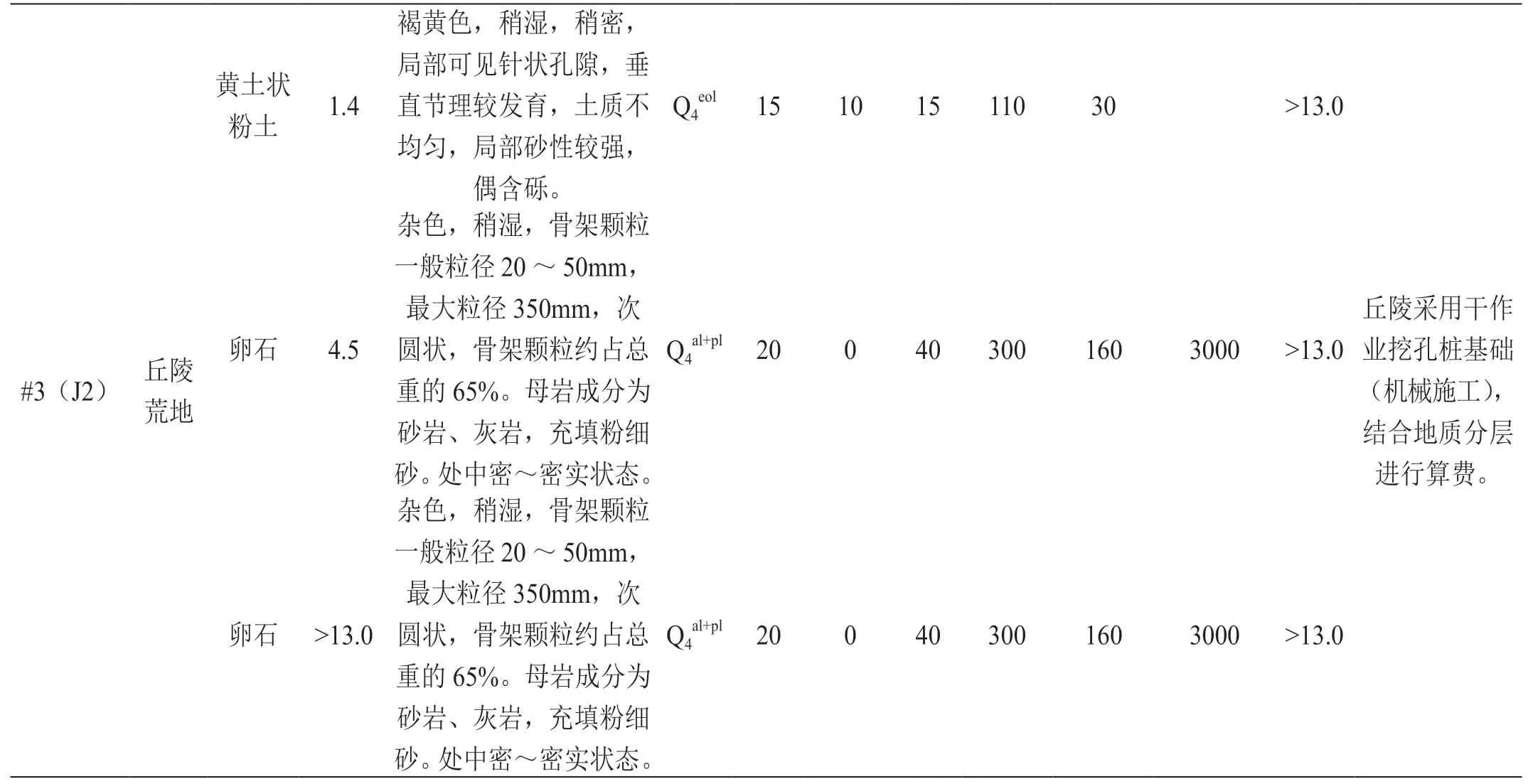
微型桩作为一种新型杆塔基础,已证实其具有一定的适用性和应用价值。但是,当前研究均是在软土和黄土土基中对其性能表现进行试验研究。而宁夏地处我国西北部,气温多变,地质条件以砂土为主,其中风沙地占宁夏总面积的11.5%,表1 为宁夏地区某35kV 线路工程地勘报告。如若在宁夏地区使用微型桩,存在以下问题并对其进行分析:

表1:35kV 某线路工程地勘报告
(1)对砂土土基的性能进行试验分析。国内学者对于微型桩在砂土中承载能力的相关研究甚少[7],而砂土土体性质与软土、黄土土体性质完全不同,需要针对砂土特征进行相应的原型试验和数值模拟,以得到微型桩在砂土中的受力特性。
(2)数值模拟的参数选择困难。在实际工程应用中,重要参数的选取一般通过现场原型试验得出或者参照其他工程的经验取值。因此,微型桩若要在砂土中进行有效应用,必须验证微型桩相关参数,可采取数值模拟与试验结果对比的方法验证参数。吴利霞等人对微型桩基础的承载性能进行了数值模拟分析,结果表明在有限元模型的基础上进行安全强度分析是可行的[8-12],但是均未考虑砂土土基情况,因此对于砂土土基中有限元模型的可靠性,需要进一步研究验证。
1.2 主要影响因素
一般情况下,桩基础的承载能力受土基和桩体本身的共同影响。影响土基性能的因素包括弹性模量、泊松比、含水率、内摩擦角等以及桩-土相互作用的影响,如接触面和摩擦系数等,桩体本身性质包括弹性模量、泊松比、桩长、桩体直径等。例如内摩擦角直接影响桩-土之间摩擦系数,弹性模量和泊松比对土体自身的承载力影响较大,图1 为某输电线路基础、地脚螺栓施工现场。

图1:某输电线路基础、地脚螺栓施工现场
对于有限元模型而言,本构模型的选取和参数的设置影响较大。常用土体本构模型有剑桥模型、Druker-Prager 模型、Mohr-Coulomb 模型、Lade-Duncan 模型等。剑桥模型常用于不排水固结饱和粘土中,Lade-Duncan 模型常用于无粘性土,Mohr-Coulomb模型适用于多种土体,适用性更加广泛[13]。
参数的设置往往直接影响到模型结果的准确性和可靠性,参数选取、初始条件设置、边界条件设置、荷载设置均需引起注意。例如土基渗透性好坏、加载速度快慢会导致孔压上发生不同程度的上升,反映了不同排水状况下的短期或长期承载力。
黄土状粉土1.4褐黄色,稍湿,稍密,局部可见针状孔隙,垂直节理较发育,土质不均匀,局部砂性较强,偶含砾。Q4 eol 15101511030>13.0#3(J2)丘陵荒地卵石4.5杂色,稍湿,骨架颗粒一般粒径20 ~50mm,最大粒径350mm,次圆状,骨架颗粒约占总重的65%。母岩成分为砂岩、灰岩,充填粉细砂。处中密~密实状态。Q4al+pl 200403001603000>13.0丘陵采用干作业挖孔桩基础(机械施工),结合地质分层进行算费。卵石 >13.0杂色,稍湿,骨架颗粒一般粒径20 ~50mm,最大粒径350mm,次圆状,骨架颗粒约占总重的65%。母岩成分为砂岩、灰岩,充填粉细砂。处中密~密实状态。Q4al+pl 200403001603000>13.0
建立模型时简化条件的选取会影响建模结果。在处理有限元模型问题时,往往需要进行一定的条件简化,这是由于实际问题的复杂度过高,模型建立困难,另外复杂的荷载和边界条件,往往会使模型结果不收敛,得不到有效结果。
2 模型计算理论
通过有限元方法,能够很好的模拟桩和土的几何形状、本构模型、边界条件等。为验证有限元计算结果的可靠性,需要与实测结果相互比较、相互印证,以便更好的理解桩的工作形状。
计算桩基承载力的方法主要主要有α 和β 两种方法。其中粘土不排水条件下的桩适用于α 方法。而β 方法是基于有效应力的分析方法,既适合于粘土又适合于砂土,根据本文所选用的土质条件,故选用β 方法来做理论分析[14,15]。
其极限摩阻力为:
式中的σv′为竖向土压力,K0为水平土压力系数。
式中η 为控制桩端破坏面性状的角度,0.33π ≤η ≤0.58π。
3 模型设置及结果分析
模型中桩基础采用线弹性模型,即小变形情况下的非线性模型。砂土地基采用Mohr-Coulomb 模型进行模拟,该模型为理想弹塑性模型,理想弹塑性材料在应力未达屈服时会发生弹性变形,达到屈服时会产生永久塑性变形且不断发展直至破坏[13]。
3.1 竖直受力模型
本文假设桩位于正常排水的砂土、无孔隙压力等。考虑到该模型的对称性,采用轴对称模型进行分析,为确保边界对分析区域的影响最低,以桩长20 米、桩径0.4m 为例,分析区域为桩端向下20 米、水平方向8 米。
对于排水条件,模拟应将时间取得足够长,以保证孔压得到充分的消散。该模型简化了实际情况,不考虑孔压即由有效应力承担全部荷载。
模型中土体为砂土,选用Mohr-Coulomb 模型模拟,
土体参数如表2所示。

表2:土体参数
桩采用线弹性模型,弹性模量E=20GPa,泊松比ν=0.2。桩土摩擦系数为0.42(即tan(0.75φ))。
对于初始应力的设置,假设土体经过一维K0正常固结,则竖向初始应力和水平初始应力为:
式中K0为初始水平压力系数,因为该模型只考虑到竖直方向的作用,不考虑水平方向,故取ν ⁄(1-ν)=0.538。偏应力q0=1-k0γ′z。
图2 给出了荷载作用下沉降曲线。由于端阻力在总荷载中占比较大,当变形比较大时才会逐渐显现,故该模型中荷载沉降曲线变化平缓,极限荷载通常取沉降为0.1 倍直径时对应的荷载约为371.2kN。

图2:荷载沉降曲线
图3 给出桩端附近的等效应力分布。η 取0.455π,有承载力系数 Nq=15.63,Nc=25.34,端阻力为
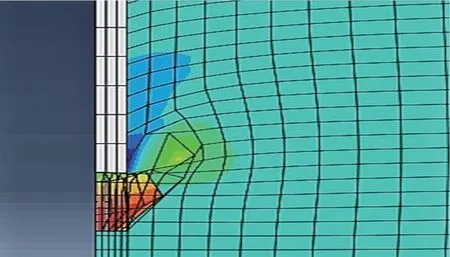
图3:桩端等效应力
有初始平均应力bNqA =(0.1×25.34+80×15.63)π×0.22=157.9kN。而桩的极限侧阻力按式(1)得 Qf=142.0kN。因而总的极限承载力为Q=Qf+Qb=299.9kN,与有限元的计算结果相差约19%左右。
不同时刻的桩侧摩阻力分布如图4所示。桩侧摩阻力自上而下的发展过程:上部的外摩擦阻力先到极限,荷载向下传递,下部外摩阻力开始变化,随后保持不变,直至最终外摩阻力呈线性分布。由于桩顶受压后侧向膨胀,导致桩端顶部土体的水平应力变大,相应的摩阻力也变大,致使桩端顶部的外摩阻力有局部的扩大趋势。由于桩端以下的破坏区向上滑动变形,迫使桩侧土体上移,造成桩端摩阻力最大值随着时间有上移的趋势。
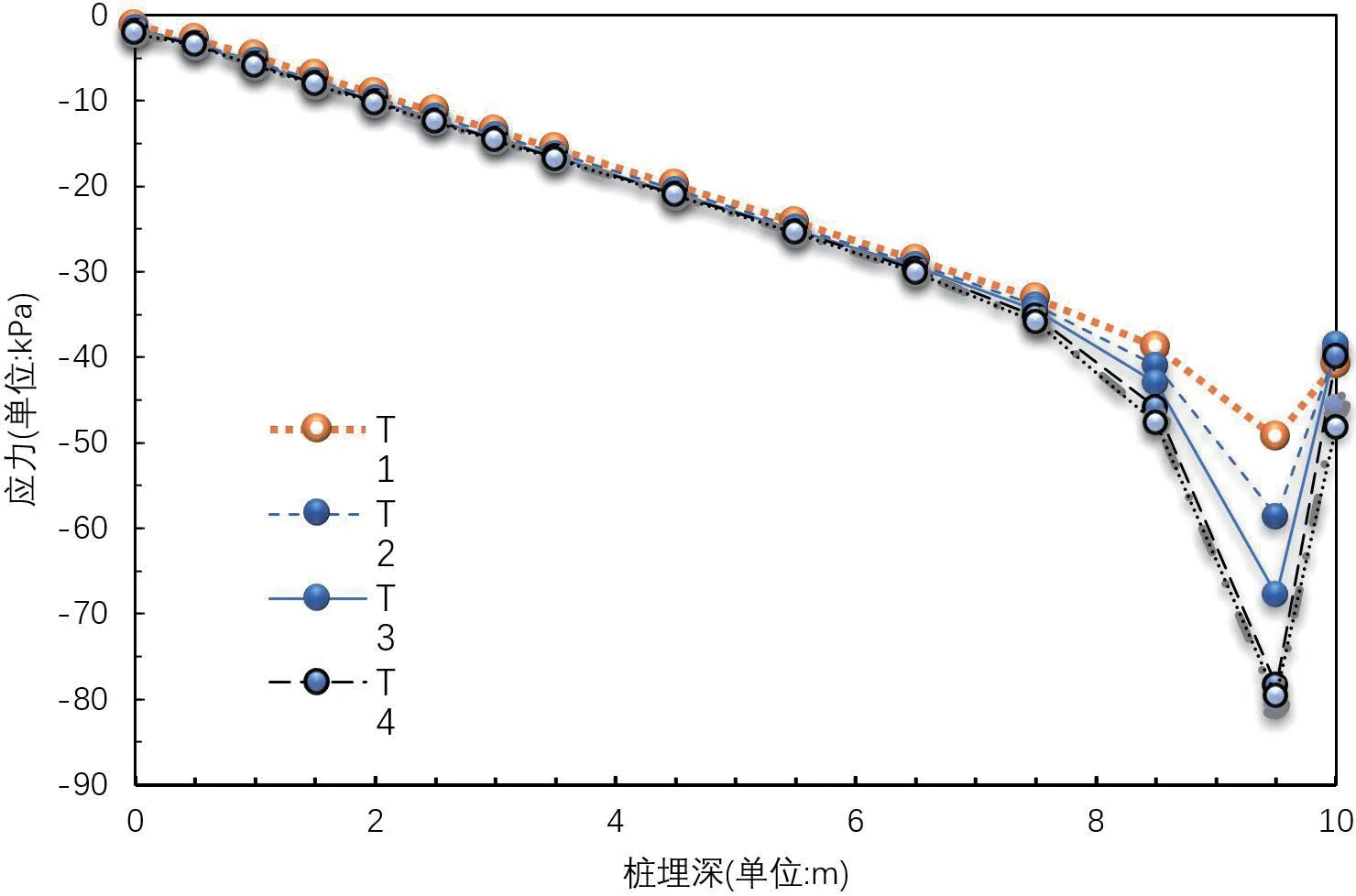
图4:不同时刻桩侧摩阻力
3.2 水平受力模型
水平荷载作用下的桩-土体系可按照桩、土相对刚度的不同划分为两类工作状态和破坏机理,即刚性短桩和弹性长桩,前者因转动或平移破坏,后者因挠曲破坏。
微型桩桩身刚度比较低,长细比大于30,柔性性能较好,可视为具有弹性长桩的破坏状态。由于水平荷载的作用,桩下段固定且不能转动,可将该类型的微型桩下段土抗力视为无限大,当桩身发生挠曲变形时,桩全长范围水平方向的桩侧土因桩水平位移增加从而逐渐出现屈服,屈服方向为从地表由下向上,桩截面的抗矩也逐渐发生变化,以便于承担桩顶渐增的水平荷载[13]。
利用有限元分析法,采用三维分析,可得出桩身弯矩和水平位移变化趋势。为避免边界条件的影响,假定桩顶承受水平荷载300kN,分析范围取桩底深20m、径向40m。桩体混凝土采用线弹性模型,桩与土之间的摩擦系数为μ=0.2,土体采用Mohr-Coulomb 模型,参数如表3所示。

表3:土体参数
该模型的建立与上述模型差异不大,分析过程为:首先进行初始应力平衡;其次加上桩体和土体实际重度之间的差值;最后采用Surface traction 荷载形式施加水平力。
桩身位移随桩埋深的分布如图5所示,有明显的弹性长桩,位移最大点出现在桩顶处约为14mm,转折点在桩身12m 处,桩身12m 以下位移近似为零,嵌固作用较为明显。
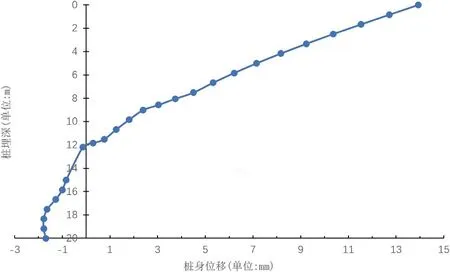
图5:桩身位移沿桩身的分布
图6 是桩身弯矩随桩埋深的曲线图,桩身弯矩先增大再减小,在距离桩顶5m 即整根桩长的1/4 处出现最大弯矩约为400kN·m。
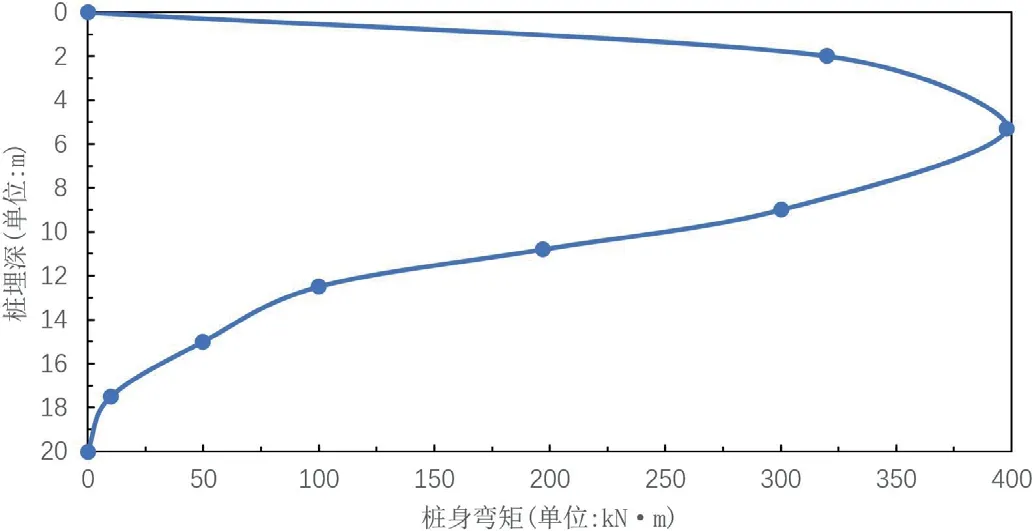
图6:桩身弯矩沿桩身的分布
3.3 模型评价
由于端阻力占总荷载的比例较大,在纵向荷载作用下沉降曲线没有出现明显转折,而且需要比较大的变形才能逐渐发挥出来。除过桩端顶部局部的扩大,总体上外摩阻力呈线性分布。
在水平荷载作用下,桩表现为明显的弹性长桩。由于土体对桩的嵌固作用,桩身12m 以下近似无位移,桩身弯矩先增大再减小,最大值在桩长1/4 处,该处位置也称之为最危险截面处。与荷载作用下的杆塔基础力学模型相比,应用该模型后的误差约为19%,误差在允许范围,进一步验证了有限元模型的正确性。
4 结论
本文介绍了一种计算微型桩基础承载力的方法,基于Mohr-Coulomb 模型的有限元计算方法,适用于砂土土基,可计算侧摩擦力、端阻力等。通过简化微型桩杆塔基础有限元模型,分析研究了基础水平和纵向荷荷,解决了桩身位移、摩擦力、弯矩、桩端阻力等荷载计算问题。
通过对单桩受力的数值模拟,对桩在土基中的受力情况,形变、位移特征有了直观准确的了解,从而更好的理解桩的工作特性。在设计上,可以参考模拟结果,提供一定的科学指导,如重点考虑1/4 截面处的弯矩问题。

