路面结构的土基应力应变近似计算

胡洪龙，谈至明

（同济大学 道路与交通工程教育部重点实验室，上海 201804）

土基竖向应力、应变是路面结构设计的重要指标.路面结构主要功能就是降低土基的竖向应力，确保土基不出现过量的变形.CBR（California bearing ratio）法即是以CBR值表征土基承载能力的一种沥青路面结构设计方法［1］.国内外学者对不同路面结构下的土基竖向应力、应变做了大量的研究.Franco Gomez-Ramirez M 等［2］根 据 NAPTF（National Airfield Pavement Test Facility）试验结果，对沥青道面下的土基顶面竖向应力、应变进行了分析.Warren等［3－4］通过建立试验路段测定了柔性基层沥青路面下的土基竖向应力大小.廖公云、朱海波等［5－6］对半刚性基层沥青路面下的土基竖向应力、应变进行了 实 测［5－6］.Child等［7］对 级 配 碎 石 基 层 水 泥混凝土路面下的土基顶面压应力进行测定，给出了荷载作用于水泥混凝土路面板不同位置时的土基竖向应力值［7］.此外，Khanal、林小平等［8－9］使用有限元方法，对不同路面结构下的土基竖向应力进行了研究.以上研究主要针对一些特定的路面结构，对土基竖向应力、应变与土基深度和路面结构参数的关系缺乏深入的分析和总结.因此，有必要对荷载作用下路面结构的土基竖向应力、应变大小及其在土基深度方向的变化规律进行深入的研究.

1 双层结构的土基应力、应变

双层结构及双圆荷载的示意图见图1.图1中，q0为均布荷载，δ为荷载圆半径，E1，E0分别为面层和土基模量，μ1，μ0分别为面层和土基的泊松比，h1为面层厚度，z为土基深度方向，x为与双圆荷载平行的方向，y为水平面上与双圆荷载垂直的方向.原点设于双圆间隙中心下的土基顶面O点.双圆荷载P＝50kN，q0＝0.7MPa，δ＝106.5mm.路面结构参数：h1＝0.1～0.7m，E1＝1 000～31 000MPa，E0＝20～200MPa，μ1＝0.15，μ0＝0.40.

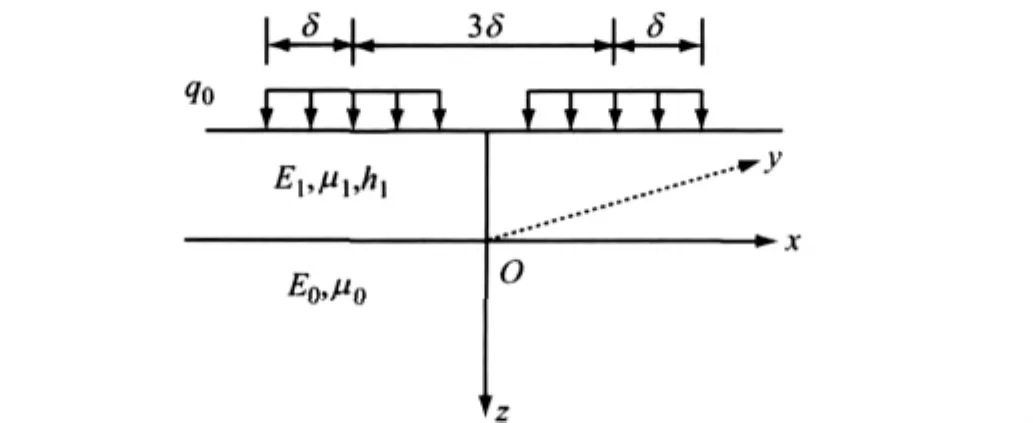
图1 双层结构及外荷载示意图Fig.1 Two layers pavement structure and loads

1.1 土基顶面应力

双圆荷载作用下的土基顶面竖向最大压应力σz0位于双圆荷载间隙中点，其值可近似为面层刚度半径l与荷载圆半径δ之比l／δ的函数［10］：

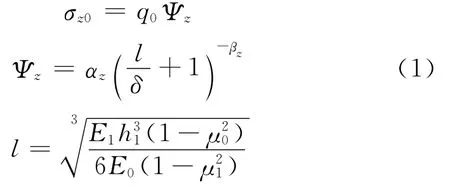
式中：αz，βz为回归系数，层间光滑时，αz＝1.60，βz＝2.03，R2＝0.998；层间连续时，αz＝1.55，βz＝2.00，R2＝0.999.

柔性基层沥青路面结构的刚度半径l一般不小于0.20m，由式（1）可推出，双圆荷载作用下的土基顶面竖向最大压应力σz0不大于130kPa；半刚性基层沥青路面结构的刚度半径l一般不小于0.25m，由式（1）可得，双圆荷载作用下的土基顶面竖向最大压应力σz0不大于96kPa.

面层与土基层间光滑，土基顶面竖向压应力最大点的x方向应力σx0和y方向应力σy0与土基顶面竖向最大压应力σz0、土基泊松比μ0之间有如下关系：

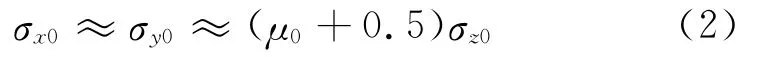
1.2 深度方向的土基应力

将土基任一深度处的最大应力σx（z），σy（z），σz（z）与土基顶面最大应力σx0，σy0，σz0之比记作θx，θy，θz即

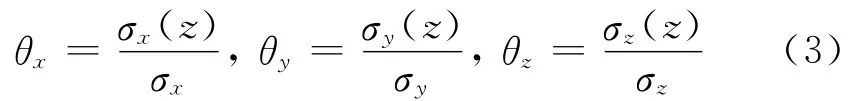
θx，θy，θz称为土基应力衰减系数，它随着土基深度z的增加而减小，随着刚度半径l的增加而增加.θx和θy大致相等，可统一记为θx，y.θx，y随土基深度增加的收敛速度快于θz.研究发现，将土基深度z、刚度半径l和荷载半径δ合并成一个参数η＝z／（l＋δ），则不同路面结构的土基应力衰减系数θx，y，θz均可视为参数的一元函数，见图2，它们的回归式可统一表示为

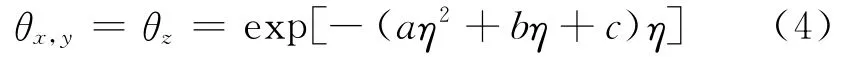
式中：a，b，c为回归系数，见表1.

1.3 土基竖向应变

多数情况下，土基任一深度处的竖向压应变最大点与压应力最大点重合，竖向压应变最大点与压应力最大点不重合时，两点处的压应变在数值上相差甚微，可近似认为其相等.根据各向同性弹性本构方程，土基任一深度处竖向最大压应变εz（z）为

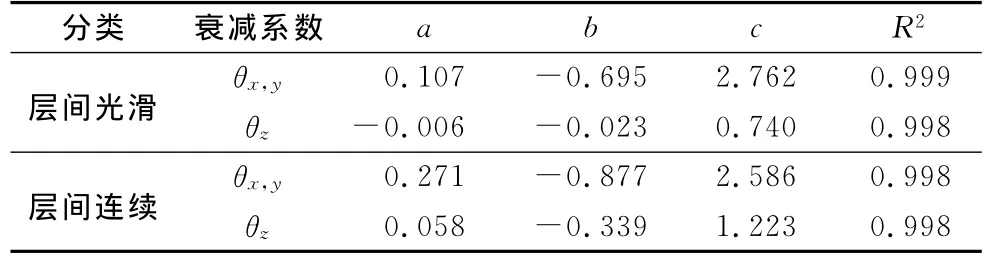
表1 式（4）的回归系数a，b，cTab.1 Regression parameters a，b，c of formula（4）

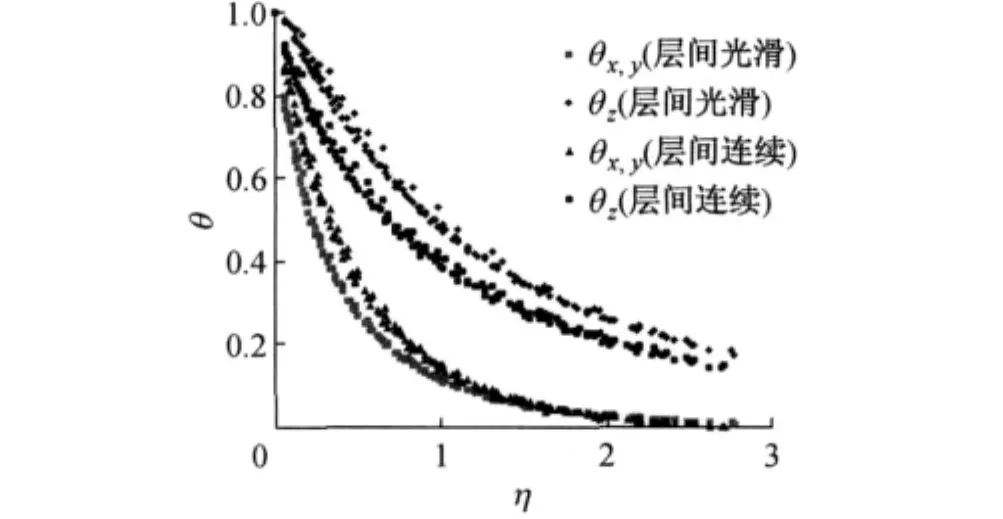
图2 土基应力衰减系数θ与η的关系Fig.2 Relationship of subgrade stresses attenuation coefficientθandη

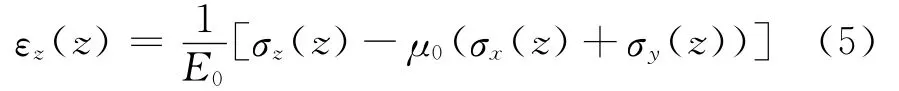
面层与土基层间光滑时，将式（2）和式（3）代入式（5）可得

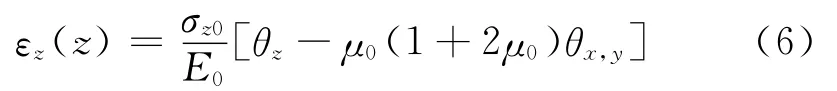
面层与土基层间连续时，回归得到土基顶面压应变εz0与土基顶面压应力σz0有如下关系：

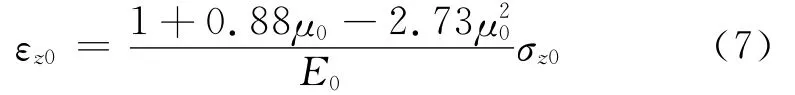
进一步可推出土基任一深度处竖向最大压应变εz（z）为

将式（1）和式（4）代入式（6）或式（8），即可得到任一深度的土基最大竖向应变值.与用BISAR软件计算结果相比，层间光滑时，两者之间的偏差小于11 μm；层间连续时，两者之间的偏差不大于12μm.

2 多层结构的土基应力、应变

路面结构有基层时，可按弯曲刚度等效原则将面层和基层合并成一层结构［11］，面层和基层总的刚度半径lg可按下式计算：

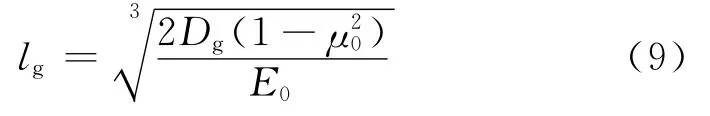
式中：Dg为面层和基层总的弯曲刚度.

式中：E2，h2，μ2分别为基层的模量、厚度、泊松比；ku为层间接触系数，层间连续时，ku＝1，层间光滑时，ku＝0.

面、基层连续，基层与土基光滑时，与理论结果相比，土基竖向的最大应力偏差不超过2kPa；最大应变的偏差小于12μm.各层之间连续时，土基竖向的最大压应力偏差不大于2kPa，最大应变的偏差小于15μm.

若路面结构超过二层，可由上而下逐层换算，先利用式（10）计算出一、二层总的弯曲刚度，再利用式（11）得出一、二层的当量结构层的模量Ex、厚度hx

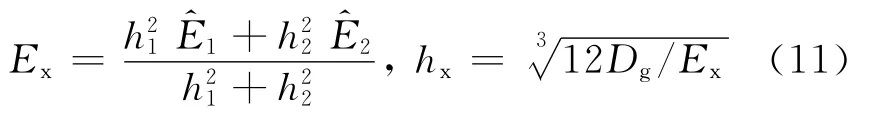
然后再由式（10）和式（11）计算出一、二、三层的当量结构层，如此换算至双层结构后，利用式（9）计算出路面结构总的刚度半径lg，最后根据式（6）和式（8）求得土基的应力、应变.

3 旁侧轮系数和邻轴系数

道路上行驶的载重车辆有单轴、双轴和三轴3类轴型.单轴荷载可视为在双圆荷载的x方向一定距离（轮距取1.8m）处又施加一个双圆荷载，新加双圆荷载对土基竖向最大应力（或应变）的影响可以用应力的旁侧轮系数ξσ（或应变的旁侧轮系数ξε）来表示；双轴荷载可视为在单轴荷载的y方向一定距离（轴距取1.4m）处再作用另一个单轴荷载，三轴荷载与之类似，新加轴载对土基竖向最大应力（或应变）的影响用应力的邻轴系数ζσ，n（或应变的邻轴系数ζε，n）来表示.因此，n轴荷载作用下，土基任一深度处的竖向最大应力σz，n（z）（或应变εz，n（z））可写成下式：

3.1 土基竖向应力

双层结构时，应力的旁侧轮系数ξσ及邻轴系数ζσ，n随着面层厚度h1、土基深度z和面层刚度半径l的变化而变化.层间光滑时，旁侧轮系数ξσ及双轮荷载时的邻轴系数ζσ，2的回归式可写成

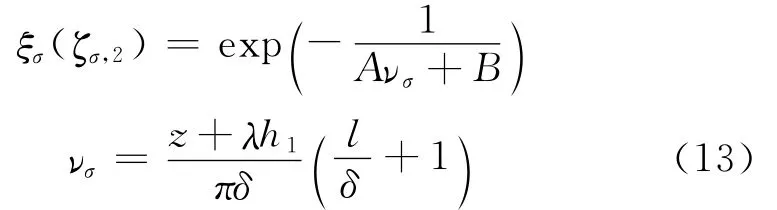
式中：νσ可称为相对深度；λ为回归系数，可近似取0.4n；A，B为回归系数，对于ξσ，分别为0.046，－0.285，R2＝0.995；对 于ζσ，2，分 别 为 0.074，－0.221，R2＝0.992.

三轴荷载时的邻轴系数ζσ，3的回归式为

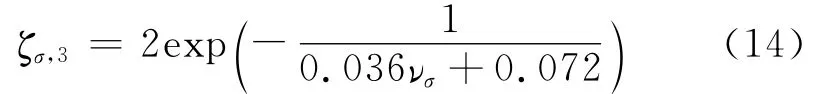
层间连续条件下ξσ，ζσ，2和ζσ，3的数值比层间光滑条件下的数值稍大，其差值一般不超过0.04，可予忽略.

3.2 土基竖向应变

应变的旁侧轮系数ξε、邻轴系数ζε，n的回归形式与应力的旁侧轮系数ξσ、邻轴系数ζσ，n的回归形式相同.双层结构层间光滑时，对于ξε，回归系数A，B分别为0.040，－0.236，R2＝0.991；对于ζε，2，A，B分别为0.065，－0.122，R2＝0.992；对于ζε，3，A，B分别为0.032，0.130，R2＝0.989.相对深度νε中回归系数λ可近似地取0.2（n－1）.层间连续条件下的ξε，ζε，2和ζε，3值稍大于层间光滑条件下的值，但其差值一般小于0.05，可予忽略.

多层结构时，旁侧轮系数ξ和邻轴系数ζ仍可按上述方法计算，只需在相对深度ν计算式中的面层厚度h1和刚度半径l分别换成路面结构层的总厚度h和总的刚度半径lg即可.

4 荷位系数

对于水泥混凝土路面而言，车辆荷载位于水泥混凝土路面板的不同位置，例如，板中、板边缘、板角隅时，土基的应力、应变是不同的.荷载位于路面板角隅时，土基的竖向应力、应变为最大，它们较上述的板中荷位的最大应力、应变之增大比例可引入荷位系数来表征，即

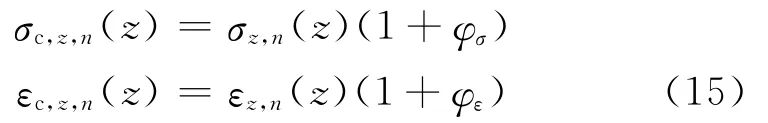
式中：σc，z，n，εc，z，n分别为荷载位于板角隅时土基的竖向最大应力、应变；φσ，φε分别为土基竖向最大应力、应变的荷位系数.

4.1 计算方法及参数

荷载位于水泥混凝土路面板角隅时的土基应力、应变采用有限元法计算，水泥混凝土路面板平面尺寸取为5m×4m，基层纵、横向加宽3m，底基层和基层同尺寸，土基相对基层横向加宽4m，纵向加宽6m，土基深度为8m，土基尺寸为17m×18m×8m.土基竖向采用不等尺寸划分为14层，上密下疏，土基单元最小网格尺寸为0.06m×0.06m.土基与底基层（或基层）层间连续或光滑，其他各层之间均光滑.

计算选取的3种路面结构参数见表2.分别计算单轴－双轮、双轴－双轮和三轴－双轮 （单轴重均为100 kN）作用下，土基顶面至深度3m范围内的竖向最大应力、应变.

表2 路面结构参数Tab.2 Pavement structure parameters

4.2 土基竖向应力

土基顶面的应力荷位系数φσ单轴时为0.70～3.50；双轴时为0.45～2.80；三轴载时为0.50～2.75.随着土基深度的增加，应力荷位系数φσ减小，当z＝3m时，φσ约为土基顶面的5%～25%.应力荷位系数φσ与相对深度νσ之间关系如图3所示，可近似表示为

土基和底基层（或基层）连续时，回归系数Cσ，Dσ值见表3.层间光滑时的应力荷位系数φσ约为层间连续时的1.05～1.20倍.

表3 荷位系数回归系数Cσ，DσTab.3 Regression parameters Cσ，Dσ

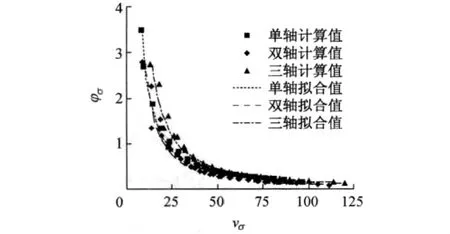
图3 层间连续时φσ－νσ关系Fig.3 φσ～νσcurve with bonded interface

4.3 土基竖向应变

土基与底基层（或基层）层间连续，单轴荷载作用于水泥混凝土板时，在土基顶面，应变的荷位系数φε在0.90～5.30之间；多轴（双轴和三轴）荷载时，φε分别在0.65～4.50和0.65～4.65之间.当z＝3 m时，φε约为土基顶面的5%～20%左右.

应变的荷位系数φε与νε之间有如下关系：

土基与底基层（或基层）层间连续时，回归系数Cε，Dε值见表4.层间光滑时应变的荷位系数φε约为层间连续时的1.10～1.25倍.

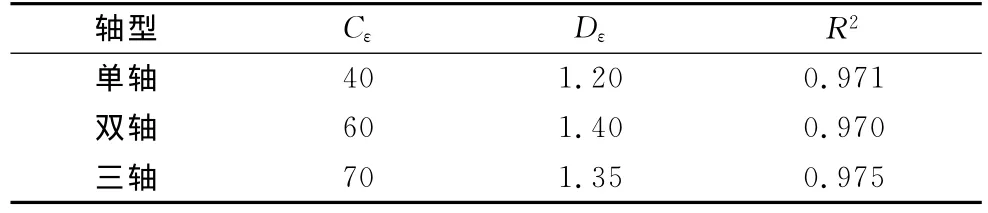
表4 荷位系数回归系数Cε，DεTab.4 Regression parameters Cε，Dε

5 结论

（1）双圆荷载作用于双层结构时，土基顶面横向（平行双圆荷载方向）应力σx0和纵向（垂直双圆荷载方向）应力σy0在层间光滑时可认为相等.在深度方向，土基横、纵向的应力收敛速度要大于土基竖向的应力收敛速度.

（2）多层结构时土基竖向应力、应变的计算可采用双层结构时的土基竖向应力、应变的计算方法，计算结果满足精度要求.

（3）单轴荷载较双圆荷载对土基竖向最大应力、应变之增大比例用旁侧轮系数ξ来表示；多轴（双轴和三轴）荷载较单轴荷载对土基竖向最大应力、应变之增大比例用邻轴系数ζn来表示.旁侧轮系数ξ及邻轴系数ζn随着相对深度ν的增加而增加.层间接触状态对旁侧轮系数ξ及邻轴系数ζ的影响不大.

（4）车辆荷载位于水泥混凝土路面板角隅时，土基竖向应力、应变最大，它们较荷载位于板中时的土基竖向最大应力、应变之增大比例可用荷位系数φ来表征.水泥混凝土路面的底基层（或基层）与土基层间光滑时的荷位系数φ值大于层间连续时的荷位系数φ值.

［1］ 姚祖康.沥青路面结构设计［M］.北京：人民交通出版社，2011.

YAO Zukang.Structural design of asphalt pavements［M］.Beijing：China Communications Press，2011.

［2］ Franco M.Gomez-Ramirez， Marshall Thompson.Aircraft multiple wheel gear load interaction effects on airport flexible pavement response ［C］／／Advanchg Airfield Pavements.Proceedings of the 2001 Airfield Pavement Specialty Conference.Chicago：American Society of Civil Engineers，2001：123-132.

［3］ Warren K A， Howard I L，Brooks J A.Preliminary construction and instrumentation plan for geosyntheticreinforced flexible pavement test sections［C］／／Geo-Frontiers 2005.Austin：Geo-Institute of the American Society of Civil Engineers，2005：4091-4096.

［4］ Isaac L H，Kimberly A W.Preliminary analysis comparing measured responses of FWD and traffic data［C］／／Geo Congress 2008：Characterization，Monitoring，and Modeling of Geo Systems. New Orleans： American Society of Civil Engineerings，2008：380-387.

［5］ 廖公云，路畅，黄晓明.沥青路面结构力学相应的分层检测与分析［J］.东南大学学报，2010，40（5）：1061.

LIAO Gongyun，LU Chang，HUANG Xiaoming.Layered measure and analysis of mechanical responses within asphalt pavement［J］.Journal of Southeast University，2001，40（5）：1061.

［6］ 朱海波，贾朝霞，张宏博，等.重载交通下的路基工作区界定问题探讨［J］.公路交通科技，2009，26（1）：39.

ZHU Haibo，JIA Chaoxia，ZHANG Hongbo，et al.Discussion of the definition of subgrade workspace under heavy traffic［J］.Journal of Highway and Transportation Research and Development，2009，26（1）：39.

［7］ Child L D，Nussbaum P J.Pressures at foundation soil interfaces under loaded concrete and soil-cement highway slabs［C］／／American Society for Testing and Materials Conference.［S.l.］：American Society for Testing and Materials，West Cohshohocken，1962：1243-1263.

［8］ Punya P Khanal，Michael S.Mamlouk.Program BIMODPAV for analysis of flexible pavements ［J］. Transportation Engineering，1997：43.

［9］ 林小平，凌建明，官盛飞，等.水泥混凝土路面路基应力水平分析［J］.同济大学学报：自然科学版，2010，38（4）：546.

LIN Xiaoping，LING Jianming，GUAN Shengfei，et al.Analysis on stress level of subgrade under cement pavement［J］.Journal of Tongji University：Natural Science，2010，38（4）：546.

［10］ 吁新华.沥青路面等效温度的研究［D］.上海：同济大学交通运输工程学院，2011.

YU Xinhua.Study on equivalent temperatures of asphalt pavement ［D］. Shanghai： College of Transportation Engineering of Tongji University，2011.

［11］ 谈至明，姚祖康.层状结构顶面当量模量的近似计算［J］.公路，2003（8）：5.

TAN Zhiming，YAO Zukang.Approximate calculation of equivalent modulus for the top of layer structure［J］.Highway，2003（8）：5.