时滞基因调控模型的稳定性与Hopf分支

宋永利，叶 子

（同济大学 数学系，上海 200092）

基因表达是指遗传物质所携带的信息从DNA传递到蛋白质的过程，是生命系统中最基本的过程，其整个过程满足一个基本的中心法则，即遗传信息通过DNA以自我为模板进行复制，以DNA为模板的RNA的合成（转录），和以RNA为模板的蛋白质合成［1］.并非所有细胞的全部基因总在不断地表达，细胞在不同时间、不同空间以不同的组合表达不同的基因，所有这些差异的关键在于基因表达过程的调控，研究基因表达的最终目的是为了了解一个复杂基因调控网络是如何工作以达到控制产物蛋白的浓度，以实现不同的生物学功能.真核细胞中常见的调控方式有：转录水平调控，即基因在何时以怎样的频率被转录；翻译调控，即细胞质中哪些mRNA被核糖体翻译；mRNA降解调控，即细胞质中哪些mRNA被去稳定化；蛋白质活性调控，即决定翻译的蛋白质的活性、抑制、区域化以及降解.

Novák和Tyson［2］针对类基因调控模型提出了关于一种反映mRNA和其控制合成的蛋白质的浓度变化的数学模型.由于mRNA在转录刚刚完成的较短时间内不能直接使用，mRNA和调控蛋白需要在细胞核与细胞质之间运输等，这就使得在基因调控模型中时滞因素是不可避免的.本文首先研究了这个模型正平衡点的存在性与稳定性；其次，探讨了时滞因素对正平衡点的稳定性的影响以及诱发的振荡现象；最后通过数值计算验证了动力学分析的理论结果.

1 正平衡点的稳定性及时滞诱发的Hopf分支

Novák和Tyson［2］提出的数学模型由以下常微分方程组来描述：

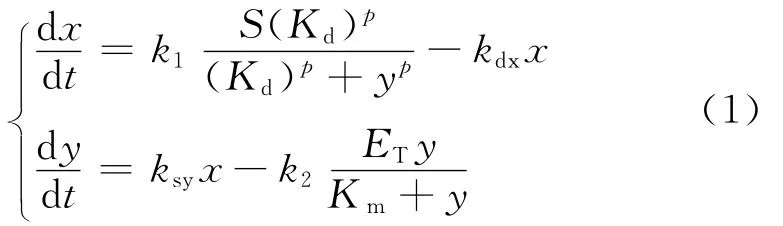
式中：x表示mRNA的浓度；y表示蛋白质浓度.蛋白质浓度的增加会对mRNA的合成起抑制作用，这里用系数为p的Hill函数表示，而蛋白质也会对自身的合成起抑制作用，这里用 Michaelis-Menten函数表示.另一方面，mRNA浓度的增加会促进蛋白质的合成，其自身还存在着降解作用.参数k1为mRNA的合成速率常数，kdx为蛋白质的降解速率常数，ksy为蛋白质的合成速率常数，k2为蛋白质抑制自身合 成 速 率 常 数，S，ET，Kd，Km为 Michaelis－Menten函数与 Hill函数中相应的常数［3－4］.

在以下研究中限定p＝2，为了方便推导，作一系列变量代换，转化为更简洁的数学形式，令k1S＝m1，（Kd）2＝m2，kdx＝m3，ksy＝m4，k2ET＝m5，Km＝m6，则方程组可 转化为以下方程组：

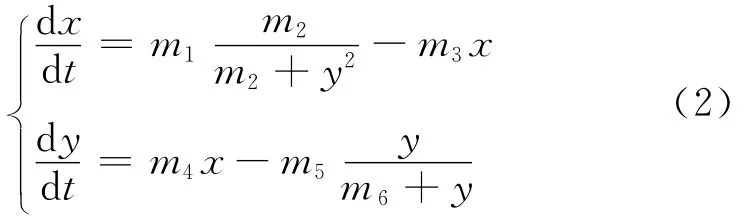
由于mi＞0，i＝1，…，6，方程组存在唯一正解，即方程组（2）有唯一的正平衡点，记为E（x＊，y＊）.下面分析该平衡点的局部稳定性.考虑方程组关于此平衡点的的线性化系统，特征矩阵为

对应的特征方程为

1.1 离散时滞

由于蛋白质的有限合成速度以及调控蛋白在细胞核与细胞质之间运输需要一定的时间，因此，mRNA的浓度事实上受当前时刻（t时刻）以前的某个时刻（比如t－τ时刻）的蛋白质的浓度的影响.为了研究这种时间滞后对基因调控模型平衡态的稳定性的影响，首先研究以下具有离散时滞的模型：

方程组（5）和（2）具有相同的平衡点E（x＊，y＊）.方程组（5）在该平衡点的线性化系统为

其中

故方程组（5）在平衡点E（x＊，y＊）的特征方程为

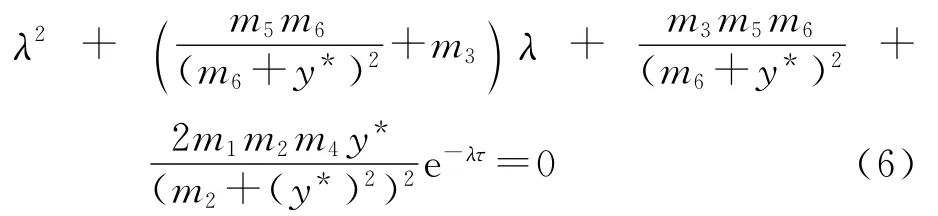
如果方程（6）有一对纯虚根±iω（ω＞0），则ω满足以下方程：

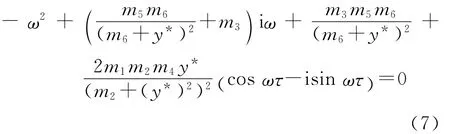
分离实部虚部得到

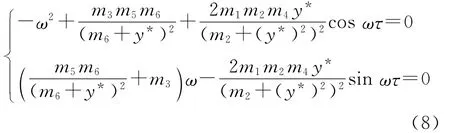
消去三角函数项，得

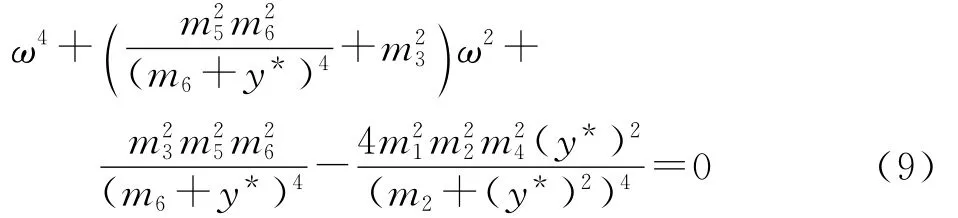
计算判别式得

因此，方程（9）只有一个正实根的充要条件是下式成立：

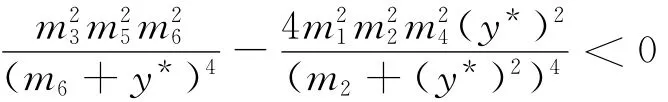
上式化简后即为

因此，当不等式（10）满足时，特征方程（6）ゆ在一对纯虚根，假设为±iω＊.

根据方程组（8）可以得到

化简上式得到

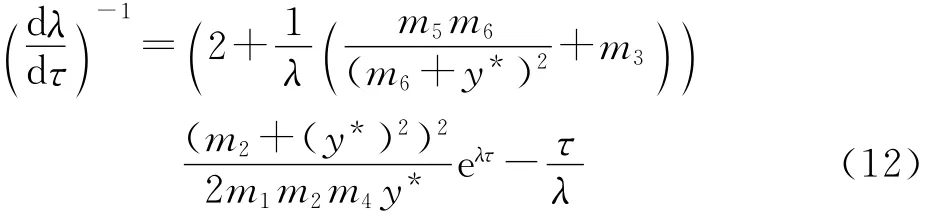
由方程组（8）和式（12），经过简单计算可以得到下式：

由式（10），（14）以及时滞微分方程的定性理论［6］，关于方程组（5）的稳定性有如下定理：

定理1 （1）如果m1m2m4m6－2m3m5（y＊）3≥0，则对任意的τ≥0，方程组（5）的平衡点E（x＊，y＊）都是稳定的.

（2）如果m1m2m4m6－2m3m5（y＊）3＜0，则当τ∈0，τ］（0时，方程组（5）的平衡点E（x＊，y＊）是渐近稳定的；当τ＞τ0时，方程组（5）的平衡点E（x＊，y＊）是不稳定的.

（3）τ＝τj是方程组（5）的 Hopf分支点.

1.2 分布时滞

由于生物体内发生的化学反应所需时间都比较长，反应物在细胞中运输所需的时间也有一定的不确定性，t时刻的mRNA的浓度与t时刻以前的一个较长时间段内的蛋白质的浓度都有关系.事实上，在生物系统中分布时滞的现象普遍存在，它更能精确刻画时滞因素的影响作用.以下研究具有分布时滞的基因调控模型.

其中时滞核函数k：［0，∞）→［0，∞）分段连续，且满足以下正规化条件

生物系统中常见的时滞弱核函数［7］为

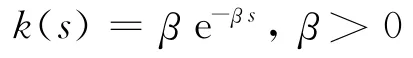
满足条件（16），其中β表示过去时间内蛋白质浓度的衰减速度.在正规化条件（16）满足时，方程组（15）和（2）具有相同的正平衡点E（x＊，y＊）.以下研究β对该平衡点稳定性的影响.

引入辅助变量u

由方程组（15）和式（17），可以得到以下关于x，y，u的三元常微分方程组：

方程组（18）的平衡点为F（x＊，y＊，y＊）.原方程组的E（x＊，y＊）的稳定性等价于方程组（18）的平衡点F（x＊，y＊，y＊）的稳定性.方程组在平衡点F（x＊，y＊，y＊）的特征矩阵为

相对应的特征方程为

根据Routh-Hurwitz判别法，方程（20）所有根皆具严格负实部的充要条件是以下3个不等式同时成立：

由于D1＞0恒成立而且

所以，方程（20）所有根皆具有严格负实部，等价于D2＞0，即

当β＝β1或β＝β2时，方程（20）具有零实部的根，由于λ＝0不是方程（20）的根，因此，假设iω（ω＞0）是方程（20）的根.将其代入方程（20），得到

由于ω不为零，故式（22）可化为

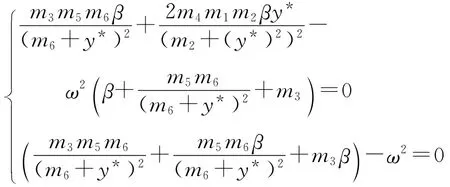
消去ω2，即得

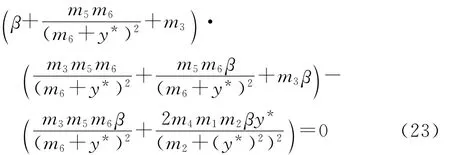
易见式（23）成立的充要条件为a2＜0且Δ＝a22－4a1a3≥0.此时，由方程组（22）得到

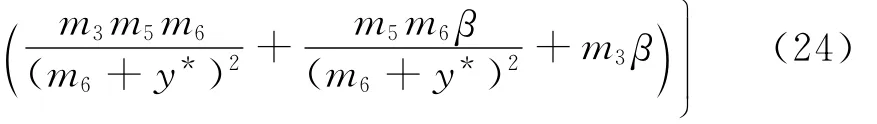
由方程组（22），式（24）可以化为

由式（25），得到

把β1，β2的值代入式（27）可以得到下式：

由以上的讨论，关于特征方程（20）的根的分布，有以下结果：

引理1 （1）假设a2≥0或a2＜0且Δ＝a22－4a1a3＜0，则对任意β∈（0，＋∞），方程的所有根皆具有严格负实部.

（2）假设a2＜0且Δ＝a22－4a1a3≥0，则当β∈（0，β1）∪（β2，＋∞）时，方程（20）的所有根皆具有严格负实部.

（3）当β＝β1或β＝β2时，方程（20）有一对纯虚根±iω；当β∈（β1，β2）时，方程（20）有一对具正实部的根.

由引理1和横截条件式（28），关于方程组（15）的正平衡点E（x＊，y＊）稳定性和分支有以下定理：

定理2 （1）假设a2≥0或a2＜0且Δ＝a22－4a1a3＜0，则对任意β∈（0，＋∞），方程组（15）的正平衡点E（x＊，y＊）都是局部渐近稳定的.

（2）假设a2＜0且Δ＝a22－4a1a3≥0，则当β∈（0，β1）∪ （β2，＋ ∞）时，方 程 组 （15）的 正 平 衡 点E（x＊，y＊）是局部渐近稳定的；当β∈（β1，β2）时，方程组（15）的正平衡点E（x＊，y＊）是不稳定的.

（3）β1和β2是方程组的Hopf分支值.

2 数值模拟

对取定的系统参数，利用Winpp软件模拟基因调控模型的数值解.取参数：m1＝0.7，m2＝0.1，m3＝0.1，m4＝1，m5＝1，m6＝0.2.则唯一的正平衡点为：E（x＊，y＊），x＊＝0.813 4，y＊＝0.872 1.

取初始值为 （x，y）＝（1，3），方程（2）的数值解曲线和相图如图1所示.图1表明，方程（2）的正平衡点是渐近稳定的.

图1 方程（2）的正平衡点渐近稳定性Fig.1 Stability of positive equilibrium of Equation（2）

以下考察离散时滞和分布时滞对此平衡点的稳定性的影响.在给定的参数值下，m1m2m4m6－2m3m5（y＊）3＝－0.118 7＜0，即式满足.首先，对具有离散时滞的方程组（5），可以计算得到：τ0≈1.799 5，τj≈1.799 5＋16.497 9j，j＝0，1，2，….

取τ＝1.6＜τ0，具离散时滞的方程（5）的数值解曲线和相图如图2所示.此时正平衡点E（x＊，y＊）仍然是稳定的.

图2 当τ＜τ0时，方程（5）的正平衡点渐近稳定Fig.2 Stability of positive equilibrium of Equation（5）is stable whenτ＜τ0

取τ＝1.8＞τ0，数值解曲线和相图如图3所示.此时正平衡点Ex＊，y（）＊是不稳定的，但在平衡点的附近存在小振幅的稳定的周期解.

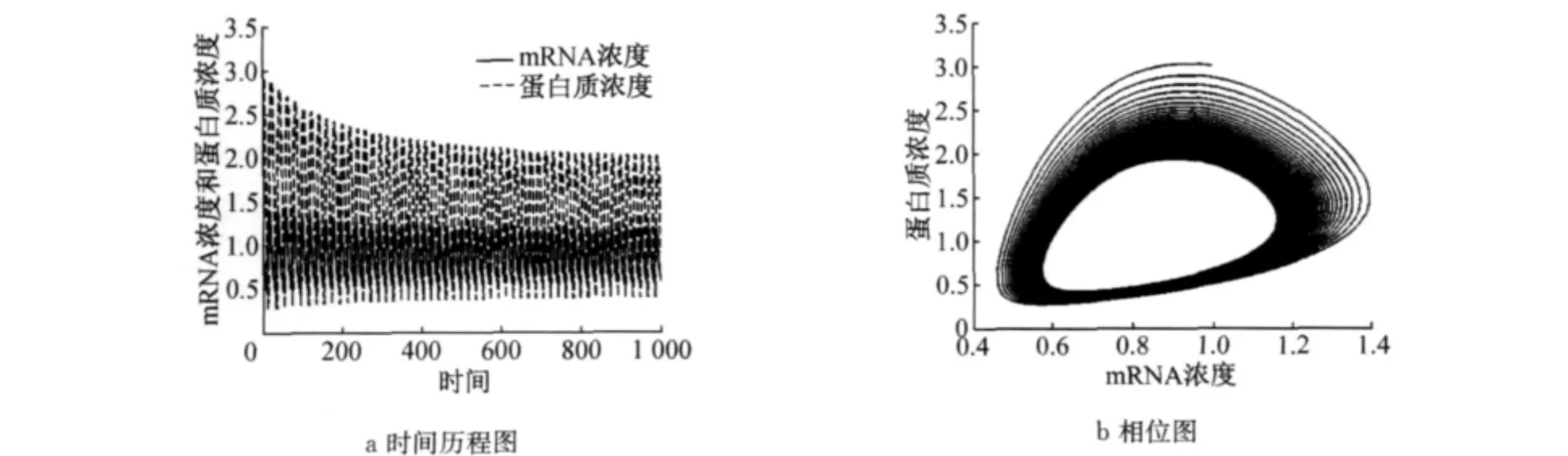
图3 当τ＞τ0时，方程（5）的正平衡点不稳定Fig.3 Stability of positive equilibrium of Equation（5）is unstable whenτ＞τ0

最后，考察分布时滞对正平衡点Ex＊，y（）＊的稳定性的影响.此时有：β1≈0.066 7，β2≈0.261 0，a2＝－0.089 8＜0，Δ＝a22－4a1a3＝0.002 8＞0.

取β＝0.03＜β1，具分布时滞的方程组（15）的数值解曲线和相图如图4所示.此时正平衡点E（x＊，y＊）仍然是稳定的.取β1＜β＝0.25＜β2，具分布时滞的方程组（15）的数值解曲线和相图如图5所示.此时正平衡点Ex＊，y（）＊是不稳定的，类似于离散时滞诱发的Hopf分支，此时在平衡点Ex＊，y（）＊的附近存在小振幅的稳定的周期解.取β＝0.45＞β2，具分布时滞的方程组（15）的数值解曲线和相图如图6所示.此时正平衡点Ex＊，y（）＊又是稳定的.

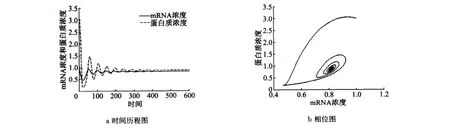
图4 当β＜β1时，方程（15）的正平衡点渐近稳定Fig.4 Stability of positive equilibrium of Equation（15）is asymptotically stable whenβ＜β1

3 结论

从本文的分析可以看出，蛋白质的有限合成速度以及调控蛋白在细胞核与细胞质之间运输所引起的时滞对基因调控模型的正平衡态的稳定性有很大的影响.在离散时滞的情况下，出现了无限个Hopf分支点，当时滞大于第一个分支点，正平衡点失去稳定性，在平衡点附近存在稳定的小振幅周期振荡.在分布时滞的情况下，出现了两个Hopf分支点，在这两个分支点所确定的区间外边，正平衡点是稳定的，而在这两个分支点所确定的区间内正平衡点是不稳定的，但有稳定的小振幅周期解存在.

对于有关生物振荡现象出现的条件：① 有负调控作用将反应中的物质不断拉向起始水平；② 负调控作用必须有足够的延迟，使化学反应不会趋于一个绝对稳定的状态；③ 动力学作用规则必须足够的非线性，使物质的稳定状态瓦解；④ 化学反应的反应和生成速率必须在一个合适的时间尺度内进行，使整个调控网络共同出现振荡现象.结合本文模型的具体环境，可以发现条件①由于mRNA和蛋白质之间存在的负调控作用显然是成立的.离散和分布时滞的引入恰好使条件②得到满足.米氏函数和希尔函数呈现明显的非线性，因此条件③满足.模型中推导的，对于周期解的出现，系数所必须满足的条件则对应条件④.

［1］ Goodwin B C. Oscillatory behavior in enzymatic control processes［J］.Advances in Enzyme Regulation，1965，3：425.

［2］ Novák B，Tyson J J.Design principles of biochemical oscillators［J］.Nature Reviews Molecular Cell Biology，2008，9：981.

［3］ 雷锦志.系统生物学——建模，分析，模拟 ［M］.上海：上海科学技术出版社，2010.

LEI Jinzhi.Systems biology—modeling，analysis，simulation［M］.Shanghai：Shanghai Science and Technology Press，2010.

［4］ Klipp E，Herwig R，Kowald A，et al.Systems biology in practice：concepts，implementation and application ［M］.Berlin：Wiley-VCH，2005.

［5］ Chow S N，Hale J K.Methods of bifurcation theory［M］.New York：Springer，1982.

［6］ Hale J K，Verduyn Lunel S M.Introduction to functional differential equations［M］.New York：Springer，1993.

［7］ Murray J D.Mathematical biology［M］.Berlin：Springer，1993.