“机械原理”课程设计中折纸机械手设计与分析
杨慧,郝亮亮,刘永斌,汪祥
(安徽大学电气工程与自动化学院,安徽 合肥 230601)
0 引言
“机械原理”课程设计是“机械原理”教学中的一个重要环节,是机械类各专业学生在“机械原理”课程学习后进行的全面、系统、深入的实践性教学,主要培养学生机械系统运动方案设计、创新设计及进行机构分析和工程设计的能力[1]。传统“机械原理”课程设计主要针对某简单机器进行机械运动简图设计,对机器人机构进行设计的较少[2-3]。折纸机器人[4-5],通过折痕构成各种回转副,从而实现其姿态变换和功能。采用折纸理论设计机器人不但能使学生学习到机构学的知识,能接受到更新的理论,而且对拓展学生的设计思路和提高就业竞争力都有重大意义[6-8]。
本文在“机械原理”课程设计中基于仿生折纸原理,创新设计出一种柔性变刚度折纸式抓捕机械手,该机械手由3根手指构成,每根手指均是Waterbomb基本折痕圆柱面,具有轻量化、多构态、大刚度的特点。首先,对其折痕的折叠方式进行几何分析。其次,采用DH坐标法进行运动分析,并利用数值法得到其可操作空间。通过该教学案例的训练,培养学生的创新能力、机械系统方案设计和结构设计的能力,以及采用先进二维绘图软件Visio和数值分析软件MATLAB进行计算、求解和仿真的能力,有意识培养学生运用所学的专业理论基础知识联系实际解决问题的能力。
1 课程设计创新的具体操作
1.1 课程设计选题
以新型折纸机械手整体结构设计为例,该机械手以3个舵机为原动件,通过绳索分别驱动3根手指。该结构要求学生对每根手指中所包含的Waterbomb基本折痕单元和每层的基本折痕进行几何分析以确定基本折痕中各个尺寸、每层中包含基本折痕单元的个数以及每根手指中包含的折痕层数。
1.2 时间安排
由于在课程设计中增加了以往没有的新题目,故该题目的课设时间增加到2周,且时间不局限于工作日,周末和晚上也允许学生在课设教室进行设计与分析。刚开始接触课程设计,学生需要一些基本知识的积累,故在开始阶段对课设进程的安排不宜太快。鉴于此,对新课设各阶段任务进行如下的时间安排:①学习绘图软件Visio,用时1.5 d,该软件主要用来绘制机械手中折痕基本单元以及单根手指中的折痕示意图;②学习数值分析软件MATLAB,用时2.5 d,该软件主要用来对几何分析和运动学分析中的公式进行求解,并绘制出相应的曲线;③查阅文献,了解折纸基本折痕的性能,1 d;④学习机器人结构和性能分析的知识,1 d;⑤单层基本折痕几何分析,用时3 d;⑥单根手指几何分析,用时2 d;⑦机械手运动学分析,2 d;⑧整理报告,准备答辩,1 d。
在软件学习方面,教师首先介绍各个软件的基本功能,并演示如何进行基本的绘图和数值求解绘制曲线,将相关的学习资料发送给学生,让学生有迹可循,避免产生盲目学习、效率低的现象。在基本折痕和单层手指几何分析方面,教师每天都在现场对学生进行指导,以确保学生快速、高效地完成任务。
2 课程设计创新的具体内容
2.1 单层基本折痕几何分析
以折纸式三指机械手为教学案例,其结构如图 1所示。每根手指均采用Waterbomb折痕基本单元,利用管状折纸弯曲时所形成的包络面进行抓捕,手指均为开链结构。
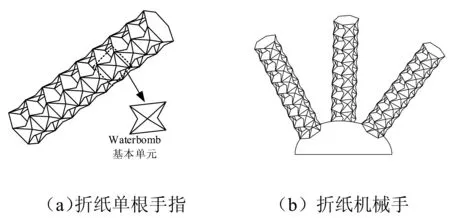
图1 折纸机械手结构示意图
利用Visio绘制基本折痕单元层,如图 2所示。每个单元层都是由n个基本折痕单元并联而成,上、下均为n边形,每边与每个Waterbomb折痕的BP、QM端形成转动副,该多边形称为上、下平台。

图2 Waterbomb折痕组成单元层的示意图
单元层的外接圆,圆半径为Re,每个Waterbomb折痕的中心点C所形成的内接圆圆半径为Ri。对于n边形的单元层有如下几何关系:
α=180°/n,Re=L0/sinα
(1)
此外,Ricosα=Ri+CDp,由图2(a)几何关系可以看出,CDp=L1cosθ,将tanα0=L1/L0代入式(1),得
Ri=L0(cot(180°/n)-cosθtanα0)
(2)
由式(2)可知,固定α0时,若α0>45°,则两谷线会发生干涉,无法完全折叠;若α0<45°,每个单元层的高度会严重减小,弯曲效果变差,显得手指粗大,故取定α0=45°。
2.2 单根手指几何分析
当机械手指弯曲时,通过手指的包络面来约束被抓取物体,因此需对手指弯曲时各基本折纸单元的参数进行分析。利用Visio绘制单根手指弯曲过程如图3所示,6个直线驱动并不是以相同的程度展开,若使单元弯曲,则需要调节几个线驱的关系。对弯曲模型的分析主要是找到每个基本折痕单元两端距离和弯曲角度θ的关系,把六边形的某镂空边作为包络端,将上、下两个基座平台单独取出,以该镂空边为分界线左右各一组,每组3条线,长度各对应相同。
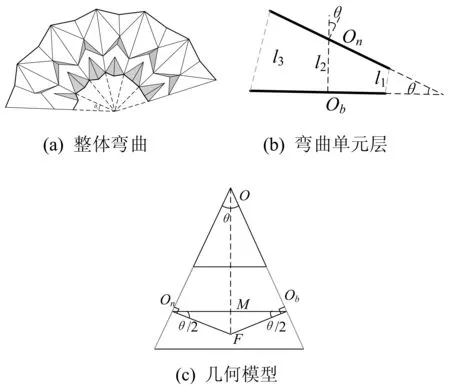
图3 单根手指弯曲示意图
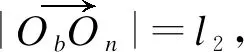
由△OOnF≃△OnMF,得出
∠FOnM=Ψ=θ/2
(3)
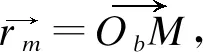
(4)
若外接圆半径为r,基座到六边形各点向量为
(5)
式中,i=1,2,3,则上、下层各点对应距离为
(6)
联合式(5)与式(7),即可得
(7)
六边形Waterbomb折痕单元两端距离与对应单元层弯曲角度的关系,先给定l2和需要弯曲的角度θ即可解出其他基本折痕单元层的距离,l2的选定也要考虑到弯曲角度,且最大距离l4不得大于2L0,即
(8)
此时l2的取值范围将会受到弯曲角度θ的限制。采用MATLAB绘制l2与θ之间的关系曲线如图4所示。
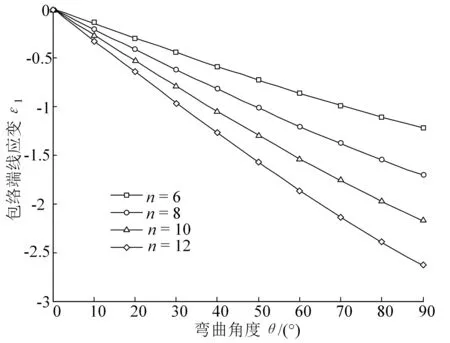
图4 线应变与弯曲角度变化关系
由图4可知,l2随θ增大而减小。当l2/L0=1时,基本单元层可以在[0,θmax]内任意弯曲,故将l2的原长定为L0,则l1在单元层弯曲时,应变为
(9)
同理,得到外侧线距l3的应变为
(10)
包络端线距l1与外侧线距l3的应变大小相同,随着弯曲角度θ的增大,内、外侧的线距l1和l3的应变也不断增大。当边数扩展至n时(n≥3),得出内外侧的线距与边数n的关系如下:
εn=sin(θ/2)/tan(180°/n)
(11)
为了使单根手指弯曲最大角度可以达到180°,则需使m≥5.36,避免m过大,选层数为m=8,该手指理论上最大弯曲角度可达268.48°,总长度为240 mm。
2.3 折纸机械手运动学分析
利用Visio绘制折纸机械手弯曲和抓取过程如图5所示。

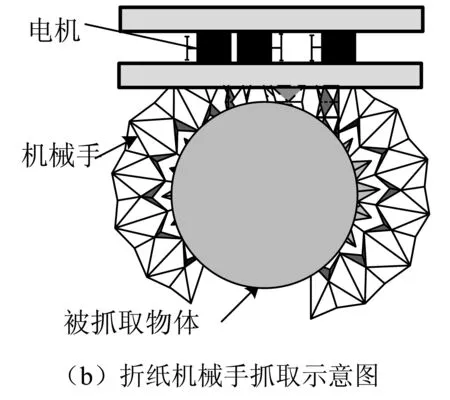
图5 折纸机械手弯曲和抓取示意图
由图5可知,每层基本折痕单元的弯曲角度是有限的,但多个单元层的弯曲效果是可以叠加的,可使手指产生较大弯曲角度θ:
(12)
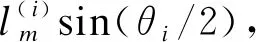
设相邻两个坐标系之间的位姿矩阵为Mii+1,由此可知,折纸手指中任一单元的包络端位置相对固定单元坐标系的坐标变换公式为
M0i=M01M12…Mi-1i
(13)
在末端单元坐标系中,包络端坐标为(L0/tan(π/6),0,0)T,于是末端单元的位姿矩阵为
(14)
以第i、j层单元的包络端位置为例,求解其对应在固定坐标系的位置,得到相邻单元的齐次变换矩阵M为
(15)
式中:i=1, 2,…, 6;j=i+1。
将式(15)代入式(13),得
(16)
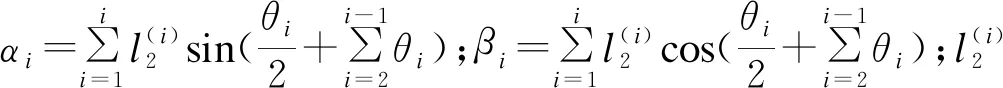
由式(14)可得,
(17)
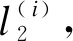
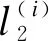
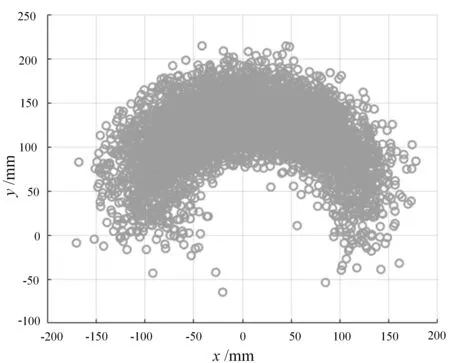
图6 折纸机械手的工作空间
图6中散点较为密集的地方为折纸机械手末端工作时出现概率较大的位置,较稀疏的地方为工作时出现概率小的位置。此外,注意到纵向位置y的取值存在负数,表明含有8层基本折痕单元的折纸机械手弯曲角度可超过180°。
3 结论
在机械原理课程设计中创新性地引入折纸式三指机械手的设计与分析,通过合理引导学生分步骤学习相关知识点,顺利完成该任务,取得较为理想的效果。该教学案例一方面使学生能够学习到较为先进的机构学知识,另一方面使学生熟练掌握了二维绘图软件Visio和数值分析软件MATLAB,提高了学生的专业技能和独立解决问题的能力。在以后的机械原理课程设计中可以适当多安排与新型科学研究相关的新设计任务,使学生能够学以致用,以更好的状态适应社会需求。

