三维微纳米台阶高精度光学显微测量量化表征

王 陈，孟宪昱，于瀛洁，孔 明，刘 维

（1.上海大学 机电工程与自动化学院，上海200444；2.中国计量大学 计量测试工程学院，浙江 杭州310018）

1 引 言

随着芯片、MEMS等高精密纳米器件小型化和集成化需求的高速增长，器件特征尺寸和与之关联的公差不断减小的同时形状结构的复杂程度却不断增加［1］，对具有良好的重复性、准确性和可靠性等特性的微纳米台阶高度测量及计量表征方法的需求也日趋迫切［2］。在半导体、微电子和纳米制造测量等领域中，台阶高度是精密光学元件、集成电路特征尺寸、石墨烯薄膜厚度、芯片等精密微纳米结构的关键特征尺寸。但是，由于微纳米结构表面三维形貌实测数据集较大，且特征突变频繁，实测数据通常含有未测点和离群值等测量缺陷，难以对其进行快速高精度表征处理。

台阶高度的定义为高低平面中距离边缘特定距离的两点的垂直距离［3］。作为微纳米计量领域中的关键几何量，其表征评定方法层出不穷，现阶段主要应用的方法包括点对点的高度提取方法（两点法）、单边法、直方图法、ISO法、最小二乘多项式拟合法等［4］。其中，ISO评定方法应用最为广泛，在最新的GPS标准ISO 25178-700［5］中，规定了基于区域的台阶高度评定方法和基于轮廓的台阶高度评定方法。但针对具有测量坏点的三维台阶形貌，目前仍未有计量表征标准。

近年来，国内外研究人员针对微纳米台阶高度测量表征难题进行了广泛研究。日本研究人员Ismail M F等针对台阶高度测量数据中出现的离群值提出了一种基于相邻数据中值的方法进行去噪表征的算法，提高了台阶高度表征的鲁棒性［6］；Le Goic G等提出了一种基于离散模态分解（discrete modal decomposition）的数学模型转换原始测量数据，结合格拉布斯检验过滤表面测量数据中离群值的方法［7］；Nurunnabi A等针对点云数据中的离群值提出了两种高鲁棒性的统计方法，结合点到平面的正交距离和局部表面点的一致性原则获得最小距离下的最大一致性点集（Maximum Consistency with Minimum Distance），进而基于局部区域中最可能的无离群值且最一致的点集估计最佳拟合平面，提高了算法的准确度和鲁棒性［8］；芬兰研究人员Heikkinen V等应用自组装的生物样品设计了5～40 nm的多级台阶高度样本，并采用多级直方图的台阶高度表征方法完成了多级台阶高度样本的表征［9］。国内的微纳米台阶高度样板的研制与测量表征研究起步相对较晚［10］，但是近年来也取得了丰硕的成果。在微纳米台阶测量表征方面，北京交通大学的谢芳等设计应用了一种结合低相干干涉和高相干干涉的绝对位移测量系统，利用两种干涉方法所获得干涉图的峰值移动范围内的条纹数量得到测量点的高度值，十次测量1 mm量块的标准差可达0.5 nm［11］；西安交通大学的杨树明等在制作8 nm、18 nm、26 nm三阶高度台阶样品的基础上，通过滤波去除低频噪音的同时利用十阶多项式拟合表面轮廓，去除高频噪声后进行台阶高度表征，提高了台阶高度拟合的准确度与鲁棒性［12］；国家计量研究院的李伟等针对台阶高度测量中的弓形误差问题，利用AFM显微镜的实测数据，将几条相邻数据进行拟合后，进而基于Sobel算子进行边缘检测，并将两条不在同一曲线上的两线段进行平移操作获得台阶高度表征结果［13］。

随着现代精密制造及测量技术的不断发展，台阶高度表征已经从传统的二维高度向三维高度转变［14］。同时，三维测量技术的不断提高使得实测多维形貌数据的数据量较传统测量方法急剧增大，数据结构更为复杂。聚类分析在大数据的分析与处理领域中具有良好的处理效果，其一方面可以作为分类预处理的处理手段，另一方面也能对数据中的异常值进行分离和识别，进而剔除离群值［15］。本文针对微纳米台阶实测形貌数据量庞大复杂，通常存在测量坏点难以实现高精度表征的难题，提出了一种三维微纳米台阶光学显微测量和量化表征方法，针对台阶结构选取测量系统并设计测量方法，建立基于K-means聚类算法的台阶高度表征模型，提高三维测量仪器实测面形数据的台阶高度表征效率，增强台阶高度表征精度和鲁棒性，并对两种不同标准样块进行测量实验，将结果与标定值进行比对，进一步验证所提出算法的可靠性。

2 台阶高度表征模型及其算法

K-means算法在本质上是基于距离相似性的度量，通过不断地迭代运算，直到其收敛到聚类中心而停止，本研究基于K-means算法提出处理测量数据并表征台阶高度的新方法，主要包括台阶高度数据维度重构、基于K-means算法的质心距离计算及数据映射、迭代收敛设计及台阶高度参数表征。

2.1 数据维度重构

台阶高度实测数据为多维面型数据，数据集庞大复杂的同时又具有低的多维特征相关性，其通常存在离群值。相比之下，低维数据处理简单，且噪声易去除，处理效率较高。因此本研究采用数据维度重构的方法将多维面型数据重构为多个二维数据集，提高数据处理效率，从而能进一步利用K-means算法的高鲁棒性表征台阶高度。

首先，将原始实测数据矩阵记录为S：

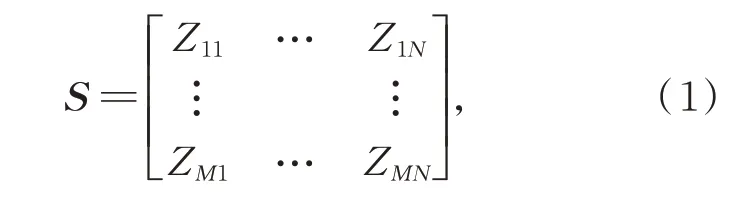
其中，S是一个M×N的矩阵（假设M为偶数，若为奇数则取M=M-1，即忽略最后一行的边缘数据）。然后将原始数据矩阵S分别选取奇数行和偶数行数据，组成奇数行数据矩阵A和偶数行数据矩阵B：

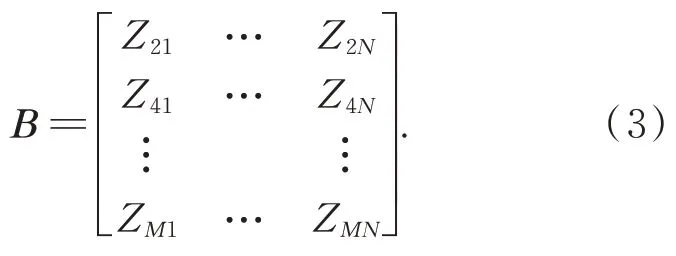
将奇数行矩阵和偶数行矩阵的同行数据提取重构为数据点矩阵S j：

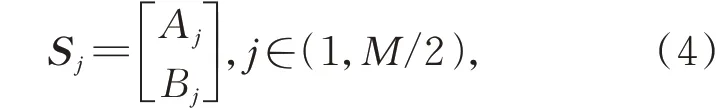
其中：A j，B j表示矩阵A和B的第j行数据。将各重构矩阵S j第一行数据作为x轴数据，第二行数据作为y轴数据，分别绘制到二维笛卡尔坐标系中。即，每个点坐标Pj，k为：

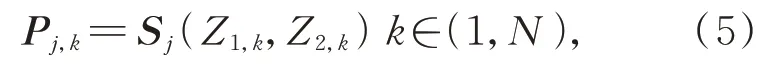
其中：Z1，k和Z2，k表示重构数据的第一行和第二行的第k列台阶高度测量值。

2.2 基于K-means算法的质心距离计算及数据映射

K-means方法又称为K均值算法，其中K代表所要聚类的数目，means表示各个维度数据所构成的簇类的数据均值，已知包含n个d维数据样本的数据集Ω={x a|x a=(x a1，x a2，…，x ad)，a=1，2，…，n}，其 中，x a是 一个d维向量，表示数据集Ω第a个数据的d个不同的属性，n是样本容量，给定一个聚类数目K，然后随机选取K个数据点分别作为初始划分的簇类中心。K-means算法通常选取欧式距离作为相似性和距离判断的准则：

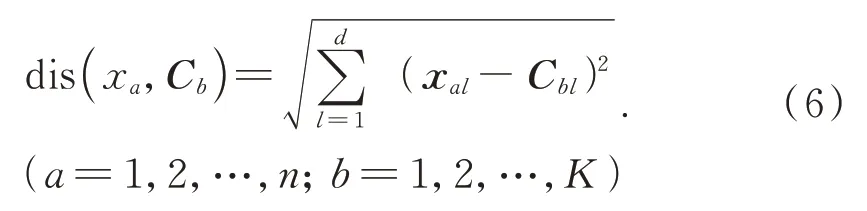
其中，C b=(C b1，C b2，…，C bd)，C b表示第b个簇类的聚类中心，每个簇类中心C b都含有d个不同的属性。

计算每个样本数据到每个聚类中心C b的距离，从而将该样本数据划分到与之最近的聚类中心所在的簇类中，通过多次迭代运算，直到簇类内所有数据的平方和最小且没有变化时为止。

台阶高度仅由高低平面之差决定，所得形貌数据具有明显的特殊性，理论上只有高台阶值和低台阶值两组数值。通过数据维度重构方法将多维面型数据降维至有序二维空间后，数据分布为明显的两个团簇，两个聚类团簇的聚类中心在高低平面数据点P1j(hlow，hlow)和P2j(hhigh，hhigh)两个点附近，故其聚类中心数量值K取2。两聚类中心的距离为：

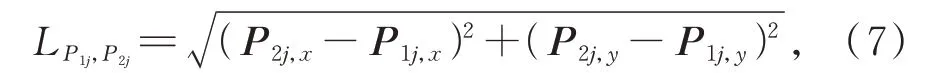
其中：P1j，x，P1j，y表 示 第j组重构数据 的 第 一 个 聚类中心在二维笛卡尔坐标系中的x、y轴坐标，P2j，x，P2j，y表示第j组重构数据的第二个聚类中心在二维笛卡尔坐标系中的x、y轴坐标。

由于原始数据通常存在离群值和噪声，为提高映射数据的可靠性，同时提高算法的鲁棒性，需要将降维后的聚类数据进行降噪处理。首先，计算同一聚类簇中的各数据值与其聚类中心的距离L，计算各点到聚类中心的距离均值Laverage和距离的方差s后，利用3σ原则，分离出离群点，并将其用聚类中心替换迭代，完成数据去噪处理。其算法流程图如图1所示。

图1 基于K-means算法的质心距离计算及数据映射流程图Fig.1 Flow chart of centroid distance calculation and data mapping based on K-means algorithm

2.3 收敛设计及参数表征

通过前述数据映射过程，将台阶高度测量所得多维面型数据映射到有序二维空间中，并以两聚类中心位置距离表征二维数据中台阶高度值的大小。为进一步保证离群值的去除率，同时提高测量精度，增强算法测量结果的稳定性和鲁棒性，在一次台阶表征的基础上多次应用上述算法进行去噪和台阶高度参数表征，直到两次相邻的测量数据的测量结果之差小于提前设定的阈值（阈值根据所需测量精度设定），则此时的算法测量结果为最终的台阶高度表征值。

根据聚类原则，两个聚类中心的横纵坐标之差理论上均为所要测量的台阶高度H j。但是，由于数据误差的存在，其聚类中心与理想值存在误差，为减少数据误差，同时增强算法的鲁棒性，在本算法中，首先计算两聚类中点间的欧氏距离，再由毕达哥拉斯定理，得单次测量的二维数据点的结果为：

将降维后的二维数据点依次处理，分别计算各降维后的二维数据组的台阶高度H j，最后将所有单次计算结果取均值，得本次数据处理后的台阶高度值为：

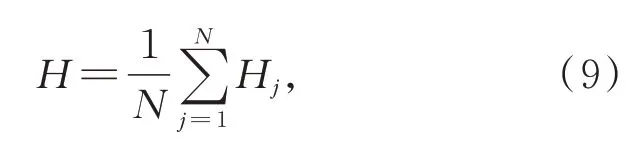
其中，N表示所有重构数据的总数。

为进一步增强表征结果的可靠性，设置收敛阈值Δ作为迭代收敛条件。阈值设计应综合考虑测量仪器的分辨率与所测对象的精度要求，首先应保证检测对象的测量精度要求，但是不得小于所用测量仪器的最小分辨率。

假设每次测量结果为H e，当H e+1-H e＜Δ时，H e即为本次台阶高度表征结果。收敛设计及最终参数表征的算法流程图如图2所示。

图2 收敛设计及台阶高度参数表征流程图Fig.2 Flow chart of convergence design and step height parameter characterization

3 实验及分析

台阶高度标准物质是指足够均匀和稳定的特定特性的物质，其特性适用于测量或者标称特性检测中的预期用途［16-17］。微纳米级台阶作为纳米测量领域重要的计量标准器具广泛应用于微纳米领域仪器（如干涉测量显微镜、轮廓仪、干涉显微镜等［18-19］）的标定与校准工作中，用以精确确定此类仪器的测量标准性并进行示值修正［20］。为验证所提出的台阶高度测量表征方法的可靠性，针对两种台阶标准物质分别选取了相应的测量系统并设计了测量方法，应用所创建的表征模型对测量获得的形貌数据进行参数化表征，将结果与标定值进行比对，并对实验结果进行了分析。

3.1 5µm台阶高度标准件实验及结果分析

应用三维形貌轮廓仪，在恒温、恒湿、洁净的实验室内对一个名义值为5μm的台阶高度标准物质进行测量实验，温度为（20±0.5）℃，湿度为（50±5）%RH，千级洁净度。如图3所示，测量设备选用为泰勒·霍普森（Taylor Hobson）非接触式表面轮廓测量仪，实验样品选取英国莱斯特（Leicester）大学制作的台阶高度标准样板，其台阶高度标定值为5.072μm，样品的测试区域选在所测量台阶高度标准件的中间区域，采用10倍物镜镜头，测量区域大小约为1 600 μm×1 600μm。

图3 泰勒·霍普森非接触式表面轮廓测量仪及测量过程Fig.3 Taylor Hobson non-contact surface profile measuring instrument and measurement process

如图4所示为本次台阶高度标准样板的实测数据三维重建结果，可以观察到有明显的离群值数据存在，例如图中红色圆圈所示。

图4 标准样板实测数据三维重建Fig.4 3D reconstruction of measured data of standard sample

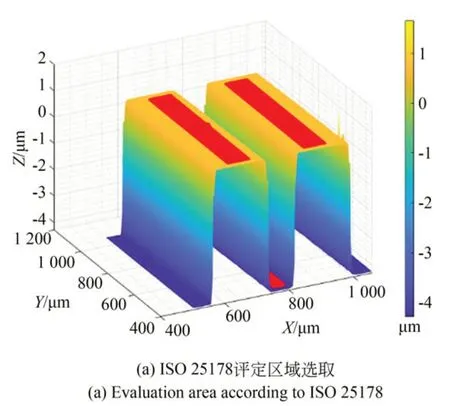
原始测量区域部分数据存在明显测量误差，为进一步减小台阶高度的表征误差，提高台阶高度表征区域的精确度，应用ISO 25178-700［5］中规定的基于区域的台阶高度评定方法选择评定区域，并应用本文提出的算法对所选取的部分区域进行数据重构，并表征台阶高度，评定区域选取如图5（a）所示，评定区域数据重建如图5（b）所示。

图5 样板实测数据的表面重建和标准工件评估Fig.5 Surface reconstruction of the measurement data and the evaluation data of the standard artefact

本次测量采用上述测量方法并应用本文所提出的表征算法得到的台阶高度表征值为5.067μm。其中，收敛设计的阈值为Δ=0.001 μm。实验表征结果与标准样板标定值的相对误差为0.1%。

3.2 90 nm台阶高度标准物质实验及结果分析

为进一步验证算法的可靠性，选用台阶高度标称值为90.5 nm的台阶高度标准样板进行测量，台阶高度标准样板如图6（a）所示。实验仪器选用为Sensofar公司生产的第五代S neox 3D光学轮廓仪，如图6（b）所示，本次台阶高度标准样板测量采用20倍物镜镜头。实验在温度为（20±0.5）℃，湿度为（50±5）%RH的恒温、恒湿条件下进行。

图6 Sensofar 3D光学轮廓仪及测量样板Fig.6 Sensofar 3D optical profilometer and step height standard artefact

通过视频显微镜将被测样板放大300倍观测本台阶高度标准样板的有效区域，如图7（上图）所示，可以明显看到表面有大量噪点。图7（下图）为利用Sensofar光学轮廓仪测量所获得的三维重构图。

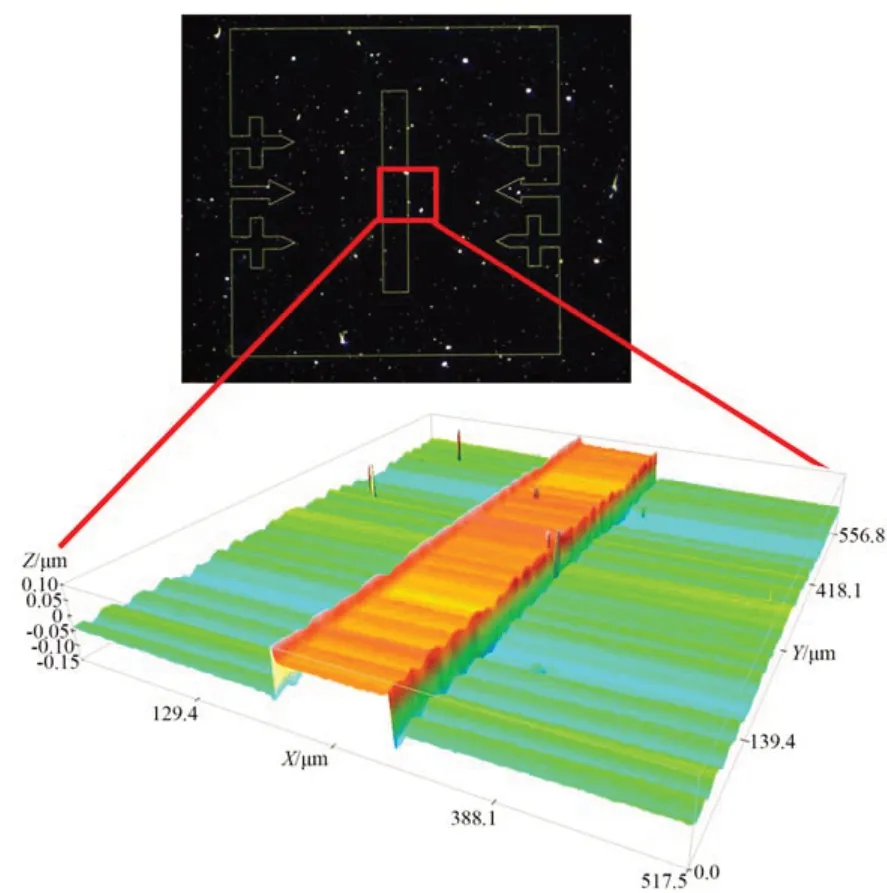
图7 台阶高度标准样板测量结果图Fig.7 Measurement results of the step height standard artefact

从三维重构图中可以看到，存在明显的数据噪点。为进一步减小台阶高度的表征误差，提高台阶高度表征精度，依据ISO 25178-700［5］中基于区域的台阶高度评定方法选择评定区域，并应用本文所提出的算法对所选取的部分区域进行数据重构。其中，收敛设计阈值Δ=0.01 nm，并将数据重构后的数据进行可视化，结果如图8（a）所示。图8（b）为本次台阶高度表征的数据分布特征。

图8 测量数据处理结果Fig.8 Processing results of measurement data

从图中可以看到，离群值基本去除，数据分布范围明显集中，台阶高度标准样板数据经过处理得到的台阶高度表征的结果为89.15 nm，表征结果可靠。

4 结 语

本文提出了一种三维微纳米台阶高度光学显微测量量化表征新方法。针对台阶特征选取合适的测量系统并设计测量方法，将测量获取的多维原始数据进行降维重组后，在台阶高度表征方面引入了聚类算法，提高了台阶高度表征效率的同时增强了表征算法对实测数据中离群值的鲁棒性，提高了测量表征精度。与传统表征方法相比，由于本算法采用聚类分析处理多维形貌数据，能够不受测量坏点的影响，快速准确获得台阶高度关键尺寸。对两种台阶高度标准物质进行了实验，通过数据重建进行可视化后，可以观察到离群值被明显去除。采用本算法对两次实验的实测数据进行处理，表征结果与标定值的误差率均在1.5%以下。所提出的方法能够高精度测量表征具有测量坏点的三维形貌数据的台阶高度值，对三维微纳米结构的测量表征具有重要的科学意义及应用价值。