地球物理反演问题中的贝叶斯方法研究
蒋星达,张 伟,杨 辉
1 哈尔滨工业大学 航天工程与力学系,哈尔滨 150006
2 南方科技大学 深圳市深远海油气勘探技术重点实验室,深圳 518055
3 南方科技大学 地球与空间科学系,深圳 518055
0 引 言
地球物理反演是研究从观测数据到地球物理模型参数映射理论和方法的一门学科(王家映,2002). 解的存在性、解的非唯一性、模型构制和解的评价是地球物理反演需要回答的四个问题(Parker, 1977). 解的存在性依赖于客观真实物理模型的存在,已被大量的理论和实际资料所证实(Tarantola, 1987; 王家映, 2002; Aster et al., 2013).解的非唯一性来源于观测数据有限以及观测数据存在误差等原因(Sen and Stoffa, 1996). 模型构制和解的评价在非线性多参数反演中主要有两种解决办法:确定性方法和统计方法(王家映,2007). 确定性方法将观测数据和模型参数看作确定量,利用数理方程或代数的方法获得唯一确定的解. 由于解非唯一性的存在,一些限制性信息(例如正则化约束)经常会加入确定性反演过程以得到人为满意的最优解(Aster et al., 2013). 然而确定性方法获得的唯一解只是真实解的近似表征,难以评价观测数据的非完备性以及误差对解的影响(Ray and Key,2012). 统计方法将观测数据和反演模型看作随机变量,基于统计学的观点求得与观测数据不同匹配程度的模型概率大小,进而利用统计参数(例如最大概率值、平均值、方差、相关系数)预测真实模型结构并给与模型参数相互关系定量评价,同时解决了模型构制和解的评价两个问题. 基于模型后验概率计算的贝叶斯方法(Bayesian inference)就是统计方法的典型代表(Tarantola, 1987).
贝叶斯方法是由Bayes(1763)初次提出,然后由Laplace(1814)进一步推导而发展出来的一种概率统计推断方法. 根据贝叶斯公式,贝叶斯方法通过事件的先验信息和采集样品推断该事件产生的后验概率. 基于贝叶斯理论中用概率描绘研究对象的特点,贝叶斯反演是在所求模型参数先验信息和由观测数据构成的似然函数的约束下,结合正演计算以及合适的采样方法推测模型参数后验概率分布的方法,从中提取的统计参数可以进行模型预测和评价(图1). 目前,贝叶斯反演已经在岩相识别、大地电磁成像、天然地震和微地震监测、流体预测等多个领域获得了广泛的应用(Guo et al., 2011; 印兴耀等, 2014; 袁成等, 2016; Pugh and White, 2018; Zhang et al., 2018; Kolbjørnsen et al., 2020). 本文在前人工作基础上系统总结了贝叶斯反演中先验信息概率分布、似然函数建立、模型参数优化、采样方法选择、后验概率推导以及反演结果评价等问题,同时对贝叶斯反演所面临的困难及未来的发展方向作出总结.

图1 贝叶斯反演一般流程Fig. 1 Flowchart of Bayesian inversion
1 贝叶斯反演基础
1.1 贝叶斯基本原理
贝叶斯公式可以表示为(Tarantola, 1987):
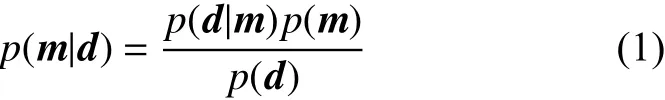
式中,d为观测数据,m为模型参数.p(m)表示模型m的先验概率分布,由先验信息确定.p(d|m)表示给定模型m时获得观测数据d的条件概率大小,称为似然函数,这一项与确定性反演方法中的目标函数相似.p(d)是观测数据d出现的概率,可以看作归一化常数,使概率值在整个模型区间内积分大小总和为1.p(m|d)是给定观测数据d的条件下模型m的条件概率,称为后验概率,表征在先验信息和观测数据共同约束下模型参数m的概率值大小(图2).
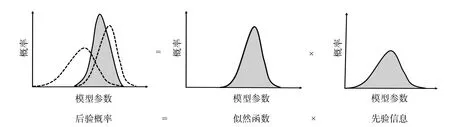
图2 贝叶斯原理示意图Fig. 2 Schematic diagram of Bayesian principle
地球物理研究在进行反演前会获得一些相关的模型参数背景知识,利用这些先验信息构建p(m)可以有效地约束反演过程. 在模型反演过程中利用观测数据d构建似然函数可以约束反演参数值的分布,根据数据噪声不同的分布情况可以形成不同的似然函数p(d|m). 结合模型的先验信息p(m)和似然函数p(d|m),通过采样方法可以推导获得贝叶斯反演模型后验概率p(m|d).
1.2 先验信息
贝叶斯理论中,先验信息是基于理论或经验对模型参数的预判,与观测数据无关. Mosegaard和Tarantola(1995)认为先验分布可以通过明确的概率密度公式表示,或者在无法确定明确表达公式时,需通过随机过程定义. 先验信息的分布形态对模型后验分布具有重要影响(Schott et al., 1999). 丰富的先验信息有利于得到更加精确的反演模型参数以及减少反演的不稳定性(Buland and Kolbjørnsen,2012; Grana, 2020).
对于没有先验知识或具有很少先验知识的非信息性先验,可以利用均匀分布(Bodin et al., 2009):
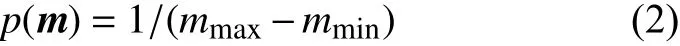
[mmin,mmax]为模型参数的下限和上限,或Jeffreys分布(Ulrych et al., 2001)等表示先验概率分布:

I(m)为Fisher信息矩阵(Robert et al., 2009).
对于提供了一定背景知识的信息性先验,先验分布高概率集中在模型参数期望值附近,低概率位于远离真解的区域. 此时高斯先验更为常用:

式中,Cm是先验模型的协方差矩阵,m0为初始模型,M为模型参数个数. 高斯分布具有平滑约束特征,相对于均匀分布,能够提供待反演参数的均值与方差,计算简单,在地震层位速度反演(Malinverno and Briggs, 2004; 肖爽等, 2020)、岩石物性反演(胡华锋等,2012)、重力密度测量(刘彦等,2015)等领域获得广泛应用.
然而高斯分布的光滑特性不利于反映某些模型参数的离散特征. 如下的柯西分布是具有“长尾巴”特征的稀疏分布:

式中,mi0和σi分别是模型参数mi峰值位置的位置参数和最大值一半处的一半宽度的尺度参数.Cm是由σi平方构成的对角矩阵. 柯西分布的值在零值附近相对更为密集,非零值附近的偏离程度比高斯先验更为自由,可以获得含有更多零值的稀疏反演结果, 在获得地层界面信息(杨培杰和印兴耀, 2008;Alemie and Sacchi, 2011; 张世鑫等, 2011; 赵小龙等,2016)和标记异常体方面应用较多(Yin and Zhang, 2014).
除去高斯分布和柯西分布,其他的分布函数也经常被采用. Theune等(2010)发现拉普拉斯分布也可以很好地分辨反演层位界面,其定义可以表示为:

Visser等(2019)认为Gamma分布可以表征反演各层的速度值,Dirichlet分布可以表征层位厚度,Poisson分布可以表征层位个数. Gamma 分布可以表示为:

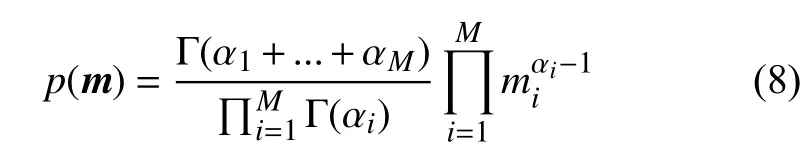

λi为模型参数mi在单位时间发生ki次的期望和方差.
何沛阳等(2020)认为截断指数分布更符合地震震级的先验分布. 截断指数的先验概率分布为:
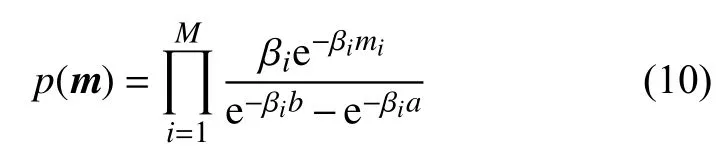
βi为模型参数mi的控制参数,[a,b]为模型参数范围.
有时单一分布并不能精确表示已知模型的先验信息,具有两个或更多特点的分布函数会被用作先验分布. 多维t分布是多维高斯分布、多维柯西分布的广义形式,可以通过变换自由度转换为高斯分布和柯西分布,印兴耀等(2014)通过测井数据统计分析发现t分布能够更好地表征弹性参数的先验分布. 多元t分布的表达形式为:

v是自由度参数,v= 1 为柯西分布,v趋于无穷大为高斯分布.
Huber分布是高斯分布和拉普拉斯分布的混合分布,可以达到在含噪情况下保持反演稳定性和小标准差处保持平滑性的特征(Guitton and Symes,2003). 印海燕(2008)认为Huber分布同样适合表征AVO反演中的纵横波速度和密度等信息. Huber分布的表达形式为:
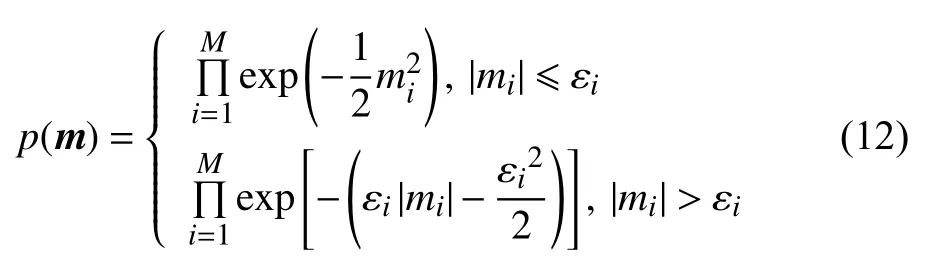
εi与模型参数mi的标准差相关.
物理模型形成过程中遵守一定的准则(例如地层速度一般具有连续性等特征),假如某模型参数的性质只与其相邻的模型参数有关,而与其他参数无关,此时可以用马尔科夫随机场构造先验信息约束模型参数. 马尔科夫随机场保证了复杂空间模型参数的连续性,在储层成像(Avseth et al., 2001;Eidsvik et al., 2004; 田军等, 2013)、岩相反演(de Figueiredo, 2019)等领域获得广泛应用. 马尔科夫随机场可以用概率公式表示为:
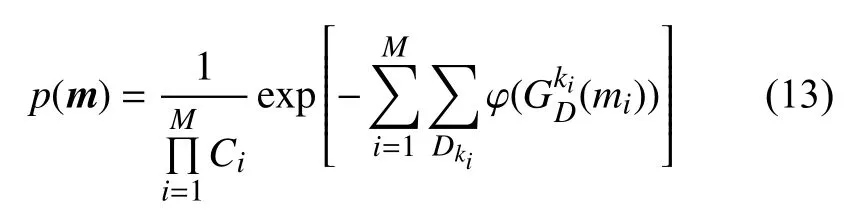
Ci为归一化常数,D表示马尔科夫随机场邻域点集,ki为邻域系统的阶数,φ为势函数;为模型参数mi关于邻域点集D的ki阶梯度函数. 此外,也有学者考虑多个分布函数同时构成先验信息约束地球物理参数反演(姚铭等,2020).
1.3 似然函数
似然函数在一定程度上反映了正演模型计算数据与观测数据的匹配程度,与数据误差和数据噪声统计特征有关. 数据误差包括测量误差和理论误差(Tarantola, 1987). 测量误差是由测量方法和观测者自身条件等外部因素影响产生的误差,理论误差来自于计算公式的近似和计算方法的限制等内部条件的影响. 数据噪声来自于记录观测数据时周围环境噪声的干扰. 由于误差和噪声难以避免且难以区分,因此将正演计算的合成数据难以拟合观测数据的部分统一视作噪声影响(Scales and Snieder,1998; Minson et al., 2014). 当观测数据中噪声服从高斯分布时,可以将似然函数用高斯函数表示(杨培杰和印兴耀, 2008; 黄捍东等, 2011; Ray and Key,2012; 苑闻京, 2012; 张繁昌等, 2014; 刘彦等, 2015;Zhang et al., 2017; Bagnardi and Hooper, 2018; Visser et al., 2019; 余小东等, 2020). 其公式可以表示为(Tarantola, 1987):
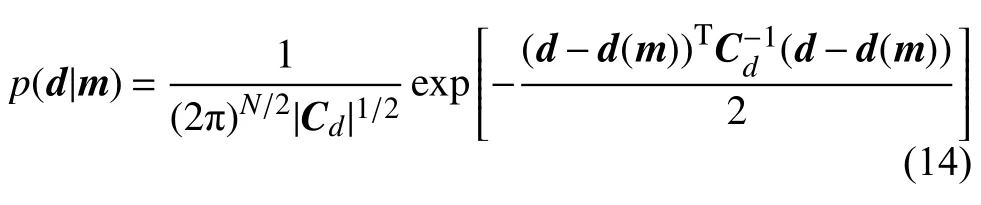
Cd是观测数据噪声和数据误差构成的协方差矩阵,d(m)为在模型m下正演计算获得的理论值,N为观测数据个数. Φ=[d−d(m)]TC−d1[d−d(m)]为拟合数据公式,与确定性反演中的目标函数相似.
当观测数据噪声存在大的异常值时,拟合数据公式采用L1范数(绝对值)而非L2范数(平方)来表征目标函数,可以有效降低大的局部异常值对结果的干扰,此时可以选择拉普拉斯分布或指数分布表征模型拟合概率大小(Tarantola, 1987;Duijndam, 1988). 拉普拉斯分布可以表示为:

依赖于噪声的分布情况,似然函数还可以选择为Dirichlet、双指数分布等函数(Tarantola, 1987;刘艳杰, 2020).
1.4 后验概率
确定先验信息和似然函数后,就可以依据贝叶斯公式构造模型参数的后验概率密度分布. 假设先验信息和似然函数均服从高斯分布,根据公式(4)和(14),后验概率密度分布可以表示为:

由此可见,后验概率密度与Cm和Cd均有关.Cm由先验信息确定,与观测数据无关,由反演参数 之间的相关性确定(Gouveia and Scales, 1998;Downton and Lines, 2001; Kjønsberg et al., 2010).当数据噪声的分布情况可以准确获得时,可以人为给定数据噪声的协方差矩阵Cd以保证反演结果的稳定性和正确性(张世鑫等,2011). 当噪声的方差和相关性存在较大不确定性时,需要对Cd进一步判断.
2 贝叶斯反演实现
2.1 优化参数
贝叶斯反演的关键是获得不同模型参数在参数空间的后验概率密度分布p(m|d). 模型参数的构成依赖于所研究的具体地球物理问题. 由于真实的物理模型是连续或复杂的,模型参数化是否合理是无法准确预知的(Sen and Stoffa, 1996; 郭荣文和柳建新, 2017). 为了能够更合理地描绘物理模型,在地球物理反演过程中有时需要校正模型参数的数量.在贝叶斯反演过程中将是否优化模型参数个数分为固定维(fixed dimensional)反演和变维(transdimensional)反演(Sambridge et al., 2006, 2013; 李承瑾等, 2018). 固定维反演仅仅优化初始模型参数值而不改变参数个数,反演过程相对简单,在地球物理的各个领域均获得广泛应用(Mosegaard and Sambridge, 2002; Chen et al., 2008; Bodin et al., 2009;Gesret et al., 2015; Zhu et al., 2016; Zhang et al.,2017; Grana, 2020). 变维反演在优化初始模型参数值的同时更新参数个数,对反演模型的结构进行充分的遍历,最终能够获得最优表征模型结构的参数维度(Sambridge et al., 2006, 2013; Bodin et al.,2012b, 2012c; Zhu and Gibson, 2018; Visser et al.,2019). 以一维模型Voronoi参数化和二维模型Voronoi参数化为例(如图3所示),在固定维反演过程中仅仅优化网格节点划分的模型参数数值而节点的个数不发生变化,而在变维反演过程中网格节点的个数也同时发生变化. 在早期贝叶斯反演过程中,由于受采样算法的限制以及有限观测数据的约束,固定维反演被广泛应用于地球物理问题求解. 近年来,随着采样算法的发展以及更多有效信息的约束,变维反演因其灵活的选择模型参数维度的特点而得到广泛的应用(尹彬和胡祥云,2016;李承瑾等,2018).
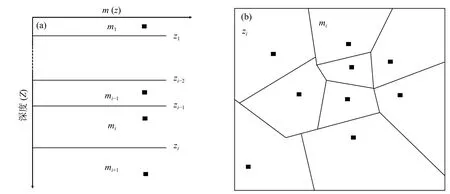
图3 模型参数化示意图.(a)一维模型Voronoi 参数化(修改自Sambridge et al., 2013);(b)二维模型Voronoi 网格参数化(修改自Bodin et al., 2012a). 方块表示网格节点,根据相邻网格节点垂直平分线确定网格边. m为模型参数,z为界面位置Fig. 3 The schematic diagram of model parameterization. (a) 1D Voronoi model parameterization (modified from Sambridge et al.,2013); (b) 2D Voronoi model parameterization (modified from Bodin et al., 2012a). The squares represent grid nodes, the grid boundaries are determined by the perpendicular bisector of adjacent grid nodes. m is model parameter. z is interface position
当贝叶斯反演过程中存在一些超参数(hyperparameter)时,如数据噪声协方差矩阵中的标准差σ,可以采用赤池贝叶斯信息准则(Akaike's Bayesian information criteria, ABIC)(Akaike Hirotugu, 1980)进行超参数预测:

p(d|mMAP,σ) 表 示超参数σ 的最大后验模型似然函数,K表示超参数的个数. Yabuki和Matsu'ura(1992)、Fukahata等(2003)、Xiong等(2021)均通过ABIC准则预估了数据噪声中的协方差矩阵大小. 除此之外,也可以将超参数看做模型参数,构建层次贝叶斯模型,反演过程中进行层次贝叶斯(hierarchical Bayesian)反演,获得包括超参数在内的各个模型参数的概率分布. Bodin等(2012a, 2012b, 2012c)通过层次贝叶斯反演准确预测了数据噪声的协方差矩阵以及速度模型参数概率分布.
2.2 反演方法
在模型参数的先验分布与似然函数均服从高斯分布且正演计算是线性的条件下,后验分布可以通过理论推导获得其高斯分布解析表达式(Tarantola,1987; Grandis et al., 1999;Malinverno and Briggs,2004;Grana, 2016;Zhu et al., 2016). 例如Buland和Omre(2003)在进行AVO反演过程中,通过线性化反射系数与速度参数和密度参数之间的关系,通过高斯先验信息和高斯似然分布获得解析的后验表达式. Grana(2016)通过泰勒展开线性化P波、S波速度以及密度与岩石的孔隙度、黏土含量和水饱和度的关系,通过高斯先验信息和高斯似然分布直接获得模型参数的后验概率分布. 但是目前的地球物理反演问题大部分为非线性多参数反演,且很难确定先验信息和似然函数均符合高斯分布,因此,要想定量评价模型参数,需要利用合适的采样算法近似求解贝叶斯模型统计参数.
直接采样法中最简便的方法是穷举法(Tarantola and Valette, 1982), 例如网格 搜寻法(grid-search method). 但在多维参数反演过程中由于穷举法遍历的模型数量过多导致其计算量过大难以获得实际应用. 蒙特卡罗法是一种随机采样方法,每次模型采样过程相对独立,不受其他采样结果的影响,在不用穷尽所有参数值的同时仍能够近似获得模型参数的后验概率分布,相比于穷举法大大降低了计算量,在贝叶斯反演中获得广泛的应用(Mosegaard and Tarantola, 1995; Minson et al.,2014). 但是蒙特卡罗法在采样过程中不受前期采样结果的指导,大量采样点落在模型参数概率较低的位置,这些模型参数对计算后验概率分布贡献较小,降低了计算效率(Grandis et al., 1999; 尹彬和胡祥云, 2016). 作为对蒙特卡罗法采样效率的提升,马尔科夫链蒙特卡罗方法(Markov Chain Monte Carlo, MCMC)将马尔科夫链更新参数过程引入到蒙特卡罗采样过程中,每次模型参数的更新均受前一个模型的指导,使采样模型更多的集中在高概率位置,便于更精确地描绘后验概率密度分布,有效提高了贝叶斯反演的采样效率. 目前在寻求后验概率问题上,针对固定维反演和变维反演问题,MCMC方法均获得了成功的应用.
2.2.1 固定维反演
在固定维反演中,Metropolis-Hastings MCMC(MH MCMC)采样(Metropolis and Ulam, 1949;Metropolis et al., 1953; Hasting, 1970)和Gibbs MCMC采样(Geman and Geman, 1984)方法应用广泛. MH MCMC方法根据Metropolis-Hastings接受准则更新模型参数. 新模型的接收概率 α (m′|m)可以表示为:
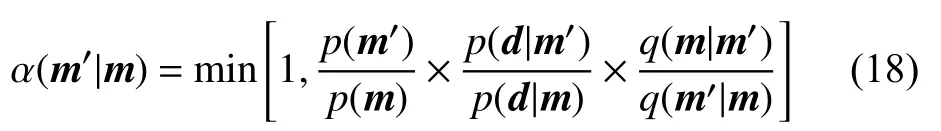
m′为 在m条件下更新获得的新模型,q(m′|m)表示模型m生成m'的概率,q(m|m′)表示模型m'生成m的概率. 将接收概率 α (m′|m)与一个产生于[0,1]随机数相比较,若 α(m′|m)较大,则新产生的模型m'被接受,否则模型m继续进入下一次循环. 迭代一定次数后在高概率参数周围采样更多,获得的概率分布更接近真实后验概率分布. MH MCMC 方法在地球物理反演问题求解过程中获得广泛应用.Kjønsberg等(2010)通过MH MCMC 算法计算储层中P波速度、S波速度和密度从而为钻井提供指导. 张广智等(2011)利用MH MCMC 方法获得地下 剖 面 的 波 阻 抗 信 息. Buland和Kolbjørnsen(2012)利用MH MCMC 算法进行可控震源电磁和大地电磁数据联合反演获得地下剖面的电阻率特征. 王朋岩等(2015)利用MH MCMC 算法反演预测储层的岩性. Bagnardi和Hooper(2018)利用MH MCMC 算法进行合成孔径雷达数据反演以获得地震事件的震源位置.
Gibbs MCMC算法是特殊的MH MCMC 算法,在每次迭代更新模型参数过程中,添加一个新的循环逐次更新每个参数值,此参数值的更新受到其他参数建议分布的影响,待所有参数更新后形成的模型进入下一次迭代,避免计算接受概率,提高了模型参数的采样效率,非常适合于高维反演问题(Sambridge et al., 2006). Gibbs MCMC采样算法在地球物理多维参数贝叶斯反演问题中获得大量的关注. Grandis等(1999)利用Gibbs MCMC采样进行大地电磁一维模型反演. Buland和Omre(2003)利用Gibbs MCMC方法从地震共深度点道集和测井数据中进行子波预测. Ulvmoen和Omre(2010)利用Gibbs MCMC算法结合叠前地震数据和井观测数据推导地下岩石/流体的位置. 张繁昌等(2014)利用Gibbs MCMC方法反演地层的波阻抗大小.
以上两种方法都是针对固定维模型参数反演,近年来随着地球物理反演精度的提高,人为主观选择特定模型参数维度引起的反演误差逐渐受到人们的关注,如何根据观测数据自行决定反演模型维度越来越成为研究的热点,此时MH MCMC和Gibbs MCMC采样方法都无法解决模型变维反演问题.
2.2.2 变维反演
为了获得合适的模型维度,一种解决办法是引入模型评价准则,例如贝叶斯信息准则(Bayesian information criterion, BIC)(Schwarz Gideon, 1978),从不同维度模型中挑选获得最优解. BIC公式可以表示为:
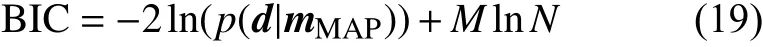
p(d|mMAP)表示在某个维度时获得的最大后验模型的似然函数.M表示模型参数维度,N为观测数据个数. 利用上述准则寻找最优模型维度时,需要首先获得每个维度下的最大后验模型,然后计算其对应的BIC值大小,最终对比每个维度计算的数值选取最小值对应的模型维度为最终维度. 上述评判标准需要在整个参数空间寻找最优解,计算量非常大(尹彬和胡祥云,2016).
Green(1995)将BIC准则与MH MCMC方法相结合,提出了支持变维反演的reversible jump MCMC(rjMCMC)算法,成为寻找最优模型参数维度的最有效算法之一. rjMCMC算法在扰动模型参数大小的同时引入“新生—消亡”过程增加或减少模型参数的个数,达到在不同维度寻找高概率模型的目的. rjMCMC 算法具有天然的稀疏特性,可以在保证拟合观测数据的基础之上获得参数最少的反演模型结构. Malinverno(2002)首次将rjMCMC算法引入到地球物理反演过程中,通过直流电阻率反演推断地层的层位个数和厚度等信息.Sambridge等(2006)将固定维反演和变维反演进行对比,用理论和实例对比阐述了rjMCMC 算法与固定维MCMC 反演结果的不同. Bodin等(2012c)利用变维反演方法通过后验概率分布大小自动确定了S波速度模型的层位个数、层位深度和层位速度值信息,准确预测了地下的层位结构(图4). Ray和Key(2012)将rjMCMC算法拓展到海洋可控震源电磁领域,通过变维反演获得一维各向异性海底电导率. Sambridge等(2013)总结了变维反演在地学领域的应用,并列举了多个rjMCMC反演的例子说明其在模型参数选择方面的灵活性. Zhu和Gibson(2018)基于rjMCMC 算法可以自动更新层位个数、速度和密度等参数的特点反演获得了地下二维波阻抗模型从而确定岩性信息. Jiang等(2021)将rjMCMC引入微地震监测速度模型校正领域,利用射孔和微地震事件校正获得能够提升事件定位精度的等效模型. rjMCMC采样方法的稀疏特性有利于灵活获得地球物理反演模型的维度信息,随着观测数据的增多、采样效率的提升以及研究领域的拓展,变维反演越来越成为贝叶斯反演研究的重点与未来发展方向.
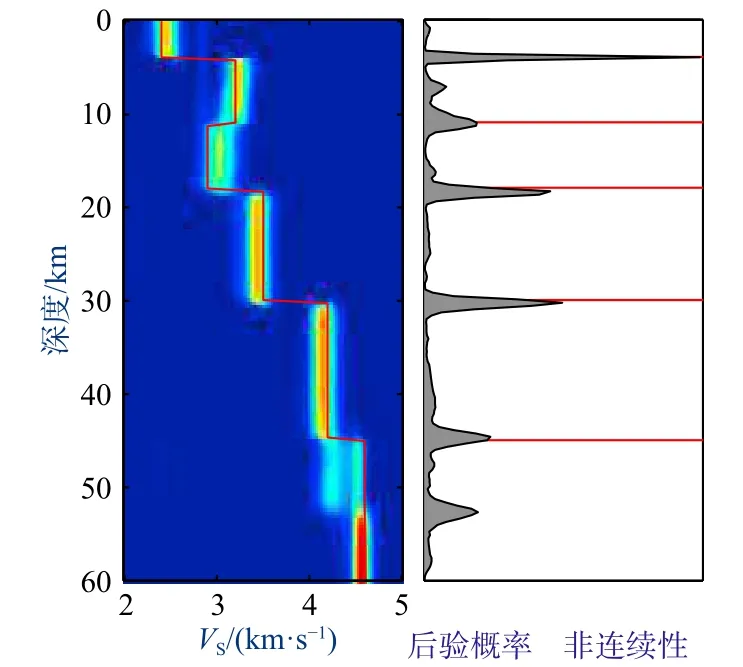
图4 根据后验概率分布确定S波速度结构(修改自Bodin et al., 2012c)Fig. 4 S-wave velocity structure determined by posterior probability density distribution (modified from Bodin et al., 2012c)
3 贝叶斯反演评价
与确定性反演唯一最优解相比,贝叶斯反演以概率形式表征不同模型参数与真实值接近程度,通过定量计算反演结果的统计参数以评估真实模型所在范围以及模型参数之间的相关性大小. 在先验信息与似然函数均服从高斯分布且正演计算是线性的条件下,后验分布可以获得解析的高斯函数表达式(Tarantola, 1987; Malinverno and Briggs, 2004). 最大后验模型mMAP与平均模型相同,根据公式(16)获得的平均模型和模型参数的后验协方差矩阵Cm′可以表示为:
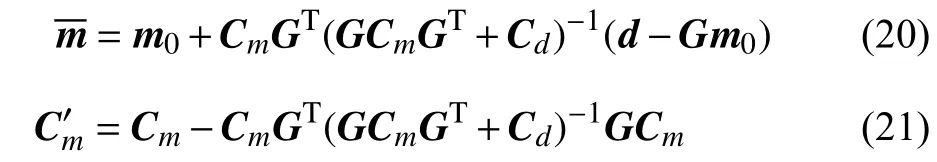
G是正演矩阵,Gm=d(m). 模型参数mi和mj的方差与相关系数即后验协方差矩阵的对角元素Cii、Cjj和非对角元素Cij:
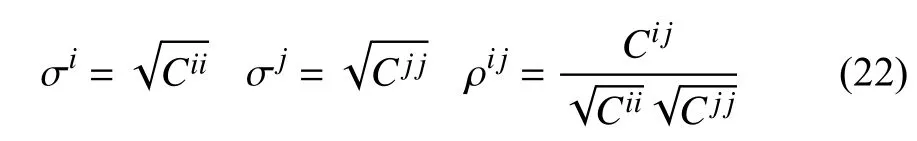
σi、 σj分别表示参数mi和mj的方差, ρij表示两个参数的相关系数. 模型参数的置信区间(68%:±1.00σ ;95%:±1.96σ)和彼此的相关系数可以定量评价反演模型的可信度和相关性.
当正演计算为非线性算子时,利用MCMC等采样方法获得的模型后验分布可以用来表征反演结果的不确定性. 最大后验概率值可直接从后验分布中提取,平均模型、模型参数的后验协方差矩阵以及参数mi和mj的1D和2D边缘概率分布p(mi|d)、p(mj|d)、p(mi,mj|d)可以通过后验分布积分获得(Tarantola, 1987; Mallick, 1995; Sen and Stoffa,1996; Dosso et al., 2014; 郭荣文和柳建新, 2017):

模型参数的方差和相关系数可以通过式(22)计算获得.
在考虑外界噪声和误差的基础上,贝叶斯反演获得的模型参数后验概率分布定量地评价了反演模型的误差范围,有效地评估了反演参数的不确定度. 通过单个模型参数的边缘概率分布可以直接评价该参数产生概率的大小. Grana(2020)通过直接展示孔隙度和泥土含量等岩石弹性参数的边缘概率分布分辨出了不同层位岩性的可能性. 最大后验模型、平均模型和协方差矩阵等统计参数可以直观定量地了解反演模型形态以及参数之间的关系. 由于以概率表示的贝叶斯后验模型参数难以获得唯一的解表征真实的物理模型,最大后验模型或平均模型经常作为真实的模型代表. 最大后验模型代表了先验信息和观测数据约束下获得的最可能的解,与确定性反演获得的最优解相同或相似(Tarantola,1987). Sacchi和Ulrych(1995)利用最大后验速度道集模型代表真实模型获得了高精度的共成像点(CMP)道集. 印兴耀等(2014)在叠前AVO反演过程中获得的纵、横波速度和密度等弹性参数的最大后验解与真实值非常相似. Zhang等(2017)在合成算例中通过贝叶斯反演获得微地震监测的最大后验速度模型参数与真实模型参数非常接近.Jiang等(2021)在速度模型变维反演过程中挑选具有最大后验概率的模型层位个数代表反演模型的维数,获得了高精度的微地震事件定位结果. 然而当先验信息较少或观测数据信噪比较低时,最大后验模型容易受到噪声的影响而与真实模型出现偏差,平均模型由于集合了高概率模型参数的平均特性而对噪声的影响有一定的抑制作用,也会被用来作为真实模型的代表. Bodin和Sambridge( 2009)利用二维Voronoi网格通过变维反演获得澳大利亚地下的速度结构并进行误差预测,平均模型与真实的地质结构非常相似,有效地识别了澳大利亚地区的速度异常,并定量评价了速度模型的不确定性. Zhu和Gibson(2018)在变维反演地层弹性参数P/S波速度值和密度过程中利用后验模型平均值代表最终的反演结果,计算获得的波阻抗界面与真实界面非常相似. 模型参数的方差或置信区间代表了反演结果的稳定性程度,方差越小或同一置信区间范围越窄表明反演结果的稳定性越高. Zhang等(2017,2018)在微地震事件位置和速度模型联合反演过程中,通过90%或95%的置信区间获得了不同位置微地震事件定位的误差范围,显示定位误差随着与检波器的距离增加逐渐增大. Visser(2019)通过P波后验模型的两个标准差展示出纵波反演速度随深度不稳定性逐渐加强. Grana等(2019)利用P/S波速度和密度等反演参数的95%置信区间进行不确定性评价,得出观测数据减少会高估反演的不确定性,而模型简化会低估反演的不确定性. 从协方差矩阵提取的相关系数可以定量评价不同模型参数的相关性大小. Zhang等(2017, 2018)通过提取速度参数和震源空间位置之间的相关系数得出它们彼此存在正相关关系,某个参数值的变大(变小)也会影响另一个参数的变大(变小),容易导致反演结果出现耦合现象. 总之,通过后验概率密度分布和其中提取的统计参数,可以定量评估模型参数的大小、离散程度和相互之间的关系. 最大后验模型和平均模型的同时求取便于更加多方位的分析模型参数,防止单个参数对最终结果的干扰(Hopcroft et al., 2007; 袁成等, 2016).
4 贝叶斯反演采样效率
目前贝叶斯反演过程中最流行和广泛应用的方法为MCMC采样方法. MCMC方法产生的大量后验模型样本有利于定量评估反演模型参数的不确定性. 然而在高维地球物理反演问题中,计算精度和计算效率总是相互制约的. 增加MCMC迭代次数有助于获得更加接近真实后验概率的模型参数分布,但是其中导致的迭代时间过长也会引起计算效率过低的问题. 迭代耗时与迭代次数和每次的迭代时间有关. 为了提高MCMC方法的计算效率同时保证计算精度,研究学者主要从迭代次数和单次迭代时间两方面着手提升MCMC方法的计算效率:(1)利用硬件资源和技术手段加速. 例如利用GPU或并行计算手段减少单次迭代计算时间或并行计算减少单链 的 迭 代 次 数(Haario et al., 2004; Buland and Kolbjørnsen, 2012; Ray et al., 2013; 余小东等, 2020).(2)开发新的MCMC方法,提高模型参数的接收率,在较少迭代次数下仍能获得接近真实的后验概率分布. 如Haario等(2006)拓展了MH MCMC算法后形成DRAM算法,Vrugt等(2008)提出的DREAM算法以及其改进型MT-DREAM算法(Laloy and Vrugt, 2012),Ray等(2013)和Sambridge(2014)利用或者改进了并行回火(parallel tempering)MCMC算法,都是在保证计算精度的同时提高了采样效率.(3)降低反演模型参数维度,用较少的模型个数代表研究区域从而减少迭代次数. 如Visser等(2019)用层位速度、层位角度和层位深度等11个参数表征二维模型,防止用网格点描绘模型带来的过量参数迭代问题.(4)探究MCMC迭代过程,通过输入较优初始模型和控制迭代步长在迭代次数较少情况下仍然获得较精确的解. 如余小东等(2020)采用电导率—深度成像的结果构建马尔科夫链的初始状态,以提高马尔科夫链的收敛性,并缩短“预热”期(burn-in period)的时间. 张广智等(2011)、Ray和Key(2012)、Amey等(2018)、Bagnardi和Hooper(2018)、余小东等(2020)通过控制迭代过程中的游走步长,确保迭代初期较早收敛到真值附近,迭代后期在真值附近能得到精度较高的估计值.(5)改进正演算法或MCMC 循环机制减少正演计算时间. 如Sambridge等(2013)采用内循环和外循环两种方式更新模型参数,在外循环中计算一次正演,在内循环中线性化正演算法基于模型更新快速计算走时变化量,大大缩减了正演走时计算时间. 除此之外,一些对MCMC方法小的改进,如模型参数二次接受以增加接收概率(Bodin and Sambridge,2009)等也有利于提高模型更新的计算效率.
5 结 论
本文从先验信息和似然函数的构建、后验概率公式的建立及求解、模型参数评价以及计算效率等方面详细介绍了贝叶斯方法在地球物理反演领域的应用. 基于概率理论,贝叶斯反演利用先验知识和观测数据对模型参数进行定量评价,从中可以获得模型参数的概率分布范围以及相互之间的关系,相对于传统方法获得的“最优解”更能体现反演结果的不确定性信息. 然而,贝叶斯反演也存在计算效率偏低从而难以解决高维反演等问题. 在结合硬件资源的条件下发展更高效的多参数、高维求解算法是贝叶斯方法在地球物理反演问题中面临的主要困难,也是未来的发展方向.
致谢
感谢南方科技大学地球与空间科学系韩鹏助理教授和日本国立统计数理研究所庄建仓副教授的宝贵意见.
附中文参考文献
郭荣文, 柳建新. 2017. 大地电磁贝叶斯反演方法与理论[M]. 长沙:中南大学出版社.
何沛阳,卢建旗,李山有,马云漪. 2020. 地震预警震级估算方法的不确定性评估模型——以τ~p_(max)法为例[J]. 内陆地震,34(4):317-329.
胡华锋,印兴耀,吴国忱. 2012. 基于贝叶斯分类的储层物性参数联合反演方法[J]. 石油物探,51(3):225-232.
黄捍东,赵迪,任敦占,王玉梅. 2011. 基于贝叶斯理论的薄层反演方法[J].石油地球物理勘探,46(6):919-924.
李承瑾,郭荣文,柳建新,刘黎明. 2018. 跨维贝叶斯反演在地球物理中的研究进展[J]. 工程地球物理学报,15(4):501-508.
刘彦,吕庆田,李晓斌,等. 2015. 基于模型降阶的贝叶斯方法在三维重力反演中的实践[J]. 地球物理学报,58(12):4727-4739.
刘艳杰. 2020. 参数反演的贝叶斯方法及其应用研究[D]. 淄博:山东理工大学.
田军,吴国忱,宗兆云. 2013. 鲁棒性AVO三参数反演方法及不确定性分析[J]. 石油地球物理勘探,48(3):443-449.
王家映. 2002. 地球物理反演理论[M]. 北京:高等教育出版社.
王家映. 2007. 地球物理资料非线性反演方法讲座(一)地球物理反演问题概述[J]. 工程地球物理学报,4(1):1-3.
王朋岩,李耀华,赵荣. 2015. 叠后MCMC法岩性反演算法研究[J].地球物理学进展,30(4):1918-1925.
肖爽,巴晶,符力耘,等. 2020. 基于高斯先验和马尔科夫随机场约束的非线性叠前地震反演研究及应用[J]. 地球物理学进展,35(6):2250-2258.
杨培杰,印兴耀. 2008. 非线性二次规划贝叶斯叠前反演[J]. 地球物理学报,51(6):1876-1882.
姚铭,高刚,胡瑞卿,等. 2020. 一种改进的贝叶斯反演算法[J]. 地球物理学进展,35(5):1911-1918.
尹彬,胡祥云. 2016. 非线性反演的贝叶斯方法研究综述[J]. 地球物理学进展,31(3):1027-1032.
印海燕. 2008. AVO叠前反演方法研究[D]. 青岛:中国石油大学(华东).
印兴耀,周琪超,宗兆云,刘汉卿. 2014. 基于t分布为先验约束的叠前AVO反演[J]. 石油物探,53(1):84-92.
余小东,陆从德,王绪本. 2020. 时间域航空电磁数据的自适应变维贝叶斯反演研究[J]. 地球物理学进展,35(5):2023-2032.
袁成,李景叶,陈小宏. 2016. 地震岩相识别概率表征方法[J]. 地球物理学报,59(1):287-298.
苑闻京. 2012. 叠前反演和地震吸收技术在复杂天然气藏地震预测中的应用[J]. 地球物理学进展,27(3):1107-1115.
张繁昌,肖张波,印兴耀. 2014. 地震数据约束下的贝叶斯随机反演[J].石油地球物理勘探,49(1):176-182.
张广智,王丹阳,印兴耀,李宁. 2011. 基于MCMC的叠前地震反演方法研究[J]. 地球物理学报,54(11):2926-2932.
张世鑫,印兴耀,张繁昌. 2011. 基于三变量柯西分布先验约束的叠前三参数反演方法[J]. 石油地球物理勘探,46(5):737-743.
赵小龙,吴国忱,曹丹平. 2016. 多尺度地震资料稀疏贝叶斯联合反演方法[J]. 石油地球物理勘探,51(6):1156-1163.

