近场强震动记录基线校正方法

张 斌，俞言祥

1 中国地质科学院地质力学研究所，北京 100081

2 自然资源部活动构造与地质安全重点实验室，北京 100081

3 自然资源部北京地壳应力应变野外科学观测研究站，北京 100081

4 中国地震局地球物理研究所，北京 100081

0 引 言

地震动是由震源释放的地震波引起的地表附近土层的振动，其对地表附近的结构破坏起主要作用. 因此，它是地震与结构抗震之间的桥梁，是工程地震研究的主要内容（胡聿贤，2006）. 地震动的物理量大多选定为与地震惯性力联系密切的强震动加速度，主要使用强震仪进行量测. 早期的强震仪主要是模拟式强震仪，其大都记录在照相纸或胶卷上，在分析之前再进行数字化预处理. 虽然模拟式强震仪对早期阶段的地震工程学的发展有极为重要的作用，但是也存在丢头、记录长周期和极大加速度的能力不足、记录数字化处理中引入长周期误差等缺点. 随着科学技术的发展，数字强震仪的出现解决了模拟式强震仪存在的问题，并具有低噪声水平、动态范围大、频带宽、采样率高、事件前记录长、数据处理简单等优点. 地震频发的国家和地区如中国、美国、日本、中国台湾等布设了越来越多的数字强震仪，获得了大批高质量的强震动加速度记录. 中国在国家第十个“五年计划”开始建设的包括1 154个永久自由场地台站、12个专用观测阵列的国家强震动观测台网（NSMONS）于2008年3月正式运行（Li et al., 2008a），记录了汶川Ms8.0地震和芦山Ms7.0地震等大震、强震以及中小震的大量强震动记录，极大地丰富了中国的强震动数据库，尤其是增加了大量的大震近场记录（Li et al., 2008b; Xie et al., 2014）.

然而，无论是模拟记录还是数字记录，近场强震动记录容易被基线偏移所污染，尤其是长周期部分. 大多数基线偏移相对于加速度时程而言几乎可以忽略不计，但是从加速度时程积分获得的速度和位移时程呈现出明显的非物理性趋势，如图1所示，芦山MS7.0地震51YAM台站NS向记录的位移时程产生抛物线形状. 地震动中包含的低频（长周期）信号和高频加速度一样对地震学和地震工程学的许多研究有非常重要的作用. 例如，速度时程的低频信号伴随着地震波的动能；地震动永久位移是研究断层破裂过程和地面变形的宝贵资料；长周期地震动信息可以用来理解远断层和近断层地震动的震源和路径相关的具体特征（Somerville et al., 1997;Somerville, 2003; Jousset and Douglas, 2007; Spudich and Chiou, 2008）；低频地震动对大型结构如高层或超高层建筑、大坝和大跨度桥梁的响应有主要的作用，会对这些长周期结构造成巨大的破坏. 近场强震动记录由于基线偏移的影响，如果不进行任何处理直接积分成位移时程，位移时程末尾部分可能与零基线有很大偏差，甚至超过地震动位移本身，无法获得可靠的地震动峰值速度（PGV）、峰值位移（PGD）、永久位移信息和长周期加速度反应谱值，限制了地震动长周期成分的可用性，在一定程度上阻碍了人们深入研究地震动长周期成分对高层或超高层建筑、大坝和大跨桥梁等长周期结构的影响. 因此，基线校正是从强震动记录中获取更多长周期信息的基本步骤.

图1 芦山MS7.0地震51YAM台站NS向原始加速度、速度和位移时程Fig. 1 Original acceleration, velocity and displacement time histories in the NS direction of 51YAM station from the Ms7.0 Lushan earthquake

1 近场强震动记录基线偏移的原因

造成近场强震动记录基线偏移的原因非常复杂，模拟强震动记录的基线误差主要来自于记录和操作. 记录误差来源于胶片和纸张翘曲、背景噪声、记录的系统噪声、基线偏移和由于模拟记录中不完整加速度产生的基线不确定性（Trifunac, 1971;Trifunac and Lee, 1974; Hudson, 1979）. 由于数字化前的放大、有限厚度的地震通道数字化和滤波等原因，导致了操作误差的产生. 数字强震仪（16位或24位记录器）的最新发展在数据质量方面取得了很大的改善. 原来存在于模拟记录中的记录扭曲和数字化误差不再存在于数字强震动数据中，其他的误差如初始基线的不确定性也得到明显改善. 然而，尽管高分辨率高采样率数字数据的质量有所提高，但基线仍然存在较大的偏移量.

1.1 低频误差

Chiu（1997）认为数字强震动记录中的低频误差是造成基线偏移的主要原因，根据低频误差的来源，将其分为仪器噪声、恒定偏移、背景噪声、初始值和操作误差等. 仪器噪声的5个典型来源包括不完善的仪器响应、分辨率不足、采样率不足、电子噪声和基线偏移. 仪器响应与平幅响应和线性相位的偏差在低频信号中较小，而在高频信号中较大. 因此，传感器的不完美响应对基线偏移的影响很小. 采样率不足会导致对应于高频信号的两个采样点之间的信息丢失. 目前常用的数字强震仪的采样率是200采样点/秒，因此采样率不足引起的误差对于低频地震动并不重要. 电子噪声水平基于仪器和仪器所处的环境，这种噪声对温度起伏非常敏感，随机波形，并在频域内分布广泛. 同时，非零背景噪声、仪器噪声和由于传感器材料疲劳也会导致基线缓慢偏移. 在日常维护中无论多久一次把仪器的基线调整到一个可接受的值，传感器弹簧的疲劳和其他未知原因也会导致额外基线偏移. 背景噪声和电子噪声的存在还会导致地震波到达前的加速度、速度和位移初始值非零，这些初始值可能导致位移波形出现较大的最终偏移. 在对数据进行处理（滤波、加零填充、渐变等）过程中可能会引入新的误差，会对校正处理的波形以及基线产生影响.

1.2 地面的倾斜或旋转

除了低频误差的影响，地面的倾斜或旋转是引起近场强震动记录基线偏移的另一个主要原因（Boore, 1999, 2001; 王 国 权 和 周 锡 元, 2004;Graizer, 2005, 2010）. 当地震发生时，近场区地表发生破裂、水平位移、隆起等强烈变形，导致强震仪产生一定的倾斜. Graizer（2005）研究了强震仪中水平摆（纵向和横向）和垂直摆运动的基本方程，如式（1）所示，强震仪的示意图见Graizer（2005）中的图1. 其中yi是 仪器的记录响应，θi是摆旋转的角度，li是 摆臂的长度，yi=θili.wi和Di分 别是第i个传感器的固有频率和临界阻尼比；g是重力加速度，是第i个 方向的地震动加速度， ψi是地表关于xi轴的旋转. 纵向和横向的方程（1a）和（1b）描述了摆在 sin(ψi)≈ψi时对低振幅运动的响应，而垂直摆对倾斜的灵敏度则大不相同，对于小的倾斜它正比于仪器在偏移 ψ角度时，水平向和垂直向加速度记录基线偏移分别可用式（2～3）计算. 假设倾斜角为0.06°，根据式（2）相当于基线偏移1 cm/s2，若从30 s开始倾斜到90 s记录结束，水平向位移时程产生的最终基线偏移可达18 m，垂直向位移时程产生的最终基线偏移只有0.9 mm（王国权和周锡元，2004）.

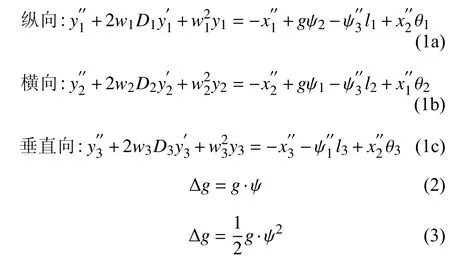
Wong和Trifunac（1977）、Graizer（1989）、Todorovska（1998）、Trifunac和Todorovska（2001）研究了等式（1a）、（1b）和（1c）右侧不同项可能的影响. 基于对一些典型强震动仪进行的数值模拟，Graizer（1989）认为倾斜会显著影响水平摆的输出. 对于具有短摆臂的典型加速度计来说，角加速度的影响很小. 对于固有频率约为100 Hz的数字加速度计来说，交叉轴灵敏度的影响也几乎可以忽略不计. 因此，倾斜对水平摆的影响总是存在的，不能忽略，而倾斜对垂直摆几乎没有影响. Graizer（2005）进行了倾斜对利用数值算法计算永久位移能力影响的试验研究，结果表明，强震动期间大或小的仪器倾斜都可能导致地面出现永久位移，加速度基线的微小变化将对最终位移产生非常大的影响. 另一方面，如果记录了强震动的六个分量（三个平移和三个旋转），则可以精确计算同震变形（Graizer, 1989, 2005; Nigbor, 1994; Trifunac and Todorovska, 2001）. 然而，目前大多数强震仪只有三个平移分量.

造成近场强震动记录基线偏移原因的复杂性导致了近场强震动记录的基线偏移类型也更为复杂，如单段线性偏移、两段式偏移、曲线式偏移、脉冲型偏移、初始偏移和多段式偏移等复杂偏移（彭小波，2011）. 因此，为了更好地应用近场强震动记录的长周期成分，必须对数据进行基线校正处理.

2 近场强震动记录的基线校正方法

理想情况下，引起基线偏移的物理机制应该是已知的，这样就可以为每个特定的记录定制一个校正方法. 然而，在大多数情况下，在处理一个特定地震的许多记录时，由于引起基线偏移的原因存在根本的不确定性，不可能针对特定地震的记录使用专门的校正方法. 目前，针对近场强震动记录基线偏移的相应校正方法大致可以分为三类：高通滤波方法、单段式或多段式校正方法和基于小波变换的方法.

2.1 近场强震动记录基线校正的准则

在地震引起的地面震动结束时，速度随时间趋于零，速度的这种特征是对任何地震动记录的合理约束，除非记录来自罕见的地震，即该地震在强烈震动后立即具有大量震后余滑. 位移随时间趋于稳定值（零或永久位移值），因为地面可以通过近地表材料的塑性响应或由于断层的同震滑动引起地壳弹性变形而发生永久变形. 在接近大地震（MW≥6.5）的断层破裂时，这种永久位移可以达到数十或数百厘米的量级. 因此，基线校正的结果需满足以下两点：（1）地震动停止后，地震动的速度趋于零；（2）位移时程的末尾段重合于或平行于零轴.

另外，全球定位系统（GPS）仪器近几十年来已在不同国家和地区广泛部署. 有些GPS仪器与强震仪相隔很近，不同震级地震都可以被数字加速度计和GPS仪器同时记录了下来. 这些数据为从强震动记录中恢复永久位移并将结果与GPS测量的同震位移进行对比验证基线校正方法的可靠性提供了良好的机会.

2.2 高通滤波方法

高通滤波方法是减少强震动加速度记录中长周期噪声应用最广泛的工具（Trifunac, 1971; Converse and Brady, 1992; Boore, 2005），也 是PEER-NGA强震动数据库数据处理的标准程序（Chiou et al.,2008; Ancheta et al., 2014）. 滤波的原理在于在截止频率的范围内（通带）滤波函数等于1，在截止频率的范围外（阻带）滤波函数等于零. 需要在通带和阻带之间进行过渡（有时称为滚降），由高通滤波截止频率和滤波阶数定义：滤波阶数越高，滚降越快（但高阶滤波的响应振荡增加）. 滤波根本的选择是在因果滤波和非因果滤波之间进行选择，非因果滤波是在时域中通过沿着记录从头到尾滤波，然后反向从记录的末尾到开头滤波来实现的，其显著特征是不会在信号中产生任何相位失真，即零相移，而因果滤波会导致记录中的相位变化（Boore and Akkar, 2003）. 为了实现零相移，非因果滤波需要在记录开始之前开始起作用，这可以通过在记录的开始和结束添加零填充来实现. 填充的长度取决于滤波截止频率和滤波阶数. 在滤波之前向加速度记录添加零填充，潜在的不良后果是在零填充与记录相邻的位置产生突然跳跃，这可能会在滤波后记录积分获得的位移时程中出现尾部翘起现象. 为了避免这种情况，通常取未加零部分的5%～10%范围使用半余弦函数来实现从记录到零填充的过渡，美国地质调查局（USGS）开发的滤波程序BAP就是采用的这种方法（Converse and Brady, 1992）.利用高通滤波处理强震动加速度记录时，最重要的问题是选择高通截止频率. Boore（2005）提出了三个同时应用的标准来选择高通截止频率：

（1）记录的傅里叶谱（FAS）与噪声模型的FAS的比值大于或等于3，从数字记录的事件前部分、从模拟记录或仪器和数字化设备的研究中获得的固定轨迹中获得噪声模型.

（2）判断记录FAS的长周期部分偏离与1/f2成正比的衰减趋势. 地震学理论表明，无论是单角频率模型（Brune, 1970）还是双角频率模型（Gusev,1983; Boore, 1986; Atkinson, 1993, 1995），加速度的FAS在低频时根据f2衰减.

（3）目视检查滤波后加速度时程的一次、二次积分获得的速度和位移时程，并判断这些速度和位移时程是否呈现非物理特征.

如果在应用滤波后将滤波后的加速度记录去除零填充，可能会导致通过积分得到的速度和位移时程基线的偏移和趋势，引起从去除零填充的加速度记录获得的速度、位移时程和加速度反应谱与未去除零填充的结果不兼容的现象. Boore（2012）针对不兼容的现象提出两种解决方法：一种是在使用去除零填充的加速度记录计算速度、位移和加速度反应谱时提供正确的初始值；另一种是对去除零填充的加速度时间序列进行后处理，即，将去除零填充的加速度时间序列两次积分成位移时间序列，用6阶多项式拟合位移时程，然后从加速度时间序列中减去拟合多项式的二阶导数.

高通滤波可以很好地消除强震动加速度记录中的长周期误差，但是大震近场的加速度记录的长周期信息和永久位移信息也会在高通滤波的过程中被滤掉，因此高通滤波方法不适用于校正大震近场的强震动记录.

2.3 基于Iwan方法的单段式或多段式校正方法

自1976年以来，已经发表了很多关于如何从大震近场强震动记录中恢复同震变形的讨论（Bogdanov and Graizer, 1976; Graizer, 1979,1989）. 后来，Iwan等（1985）和Chiu（1997）提出了对数字强震动记录进行基线校正的方法. 在Chiu（1997）的方法中，强震动记录在积分前需要先进行高通滤波. 因此，它可以恢复部分而不是全部发生的永久位移，他的方法更适合地震工程目的. Iwan等（1985）表明基线偏移是由当加速度超过50 cm/s2时PDR-1/FBA-13型数字强震仪系统机械或电路的微小磁滞效应引起的，基线偏移在强震段期间（t1～t2）可能以复杂的方式发生变化，强震段后的结束段（t2～tend）基线偏移可能与强震段的基线偏移不同，t1和t2分别是强震段和结束段的开始时间，tend是记录结束的时间. Iwan等（1985）提出从原始加速度记录相应时间段去掉两个基线偏移：t1和t2之 间的am、t2和tend之间的af，如图2所示.am值是在强震段发生的基线复杂变化的平均值.af由强烈震动后速度时程的线性拟合斜率决定：

图2 Iwan等（1985）两段式校正方法原理图（修改自Wu and Wu, 2007）Fig. 2 Schematic diagram of Iwan et al. (1985) two-stage baseline correction method (modified from Wu and Wu, 2007)

vf直线是通过对速度时程的t2到记录结束部分进行最小二乘拟合得到.am由校正后的最终速度平均为零决定. 如果在t1～t2间隔结束时基线校正的速度am(t2−t1)等 于拟合直线的速度vf(t2)，则满足此要求：

方法的关键是t1和t2时间点的选择. Iwan等（1985）选择加速度的绝对值首次超过50 cm/s2的时间为t1， 对于t2提出了两个具体选项：（1）t2是加速度永远不会超过50 cm/s2的时间；（2）选择t2以最小化最终位移.

Iwan等（1985）的基线校正方法是针对特定仪器传感器的迟滞效应导致的基线偏移，不同国家和地区布设的强震仪也不尽相同，因此该方法可能并不适用于其他地震的强震动记录，如使用Iwan等（1985）的校正方法对1999年的集集地震就没有带来令人满意的结果（Boore, 2001）. Boore（1999, 2001）、王国权和周锡元（2004）、Graizer（2005）认为还必须考虑地面倾斜的影响. 因此，Boore（2001）在处理集集地震近场强震动记录时建议将t1作为一个自由参数，而不是由震动阈值决定，t2可 以取t1和记录结束之间的任意值，只要记录结束附近的平均校正速度为零. 选择t2作为拟合速度的直线变为零的时间：

Boore（2001）将其称为v0校正. 结果表明，若t2为t1～tend之间任意自由参数时，最终位移的范围可能很大，但是周期小于20 s的位移反应谱通常不受基线校正的影响. 王国权和周锡元（2004）采用相似的v0校正方法处理了集集地震的近场强震动记录.v0校正方法仅适用于最简单的单段线性偏移情况，选取拟合速度时程末尾时间段更多的是根据主观经验，并没有给出为何选取该时间段进行速度时程的最小二乘拟合. 拟合时间的细微变化都会影响拟合直线斜率以及与时间轴交点的变化，进而导致积分后的位移相差较大. 并且使用最小二乘法拟合该时间段的速度时程，对于一些记录，会出现拟合直线与时间轴的交点时间t2为负值或超出时间轴范围的情况. 于海英等（2009）也基于Iwan方法的原理对汶川地震的部分近场强震动记录进行多段式校正. 这些方法可以有效地处理相应地震的大部分近场强震动记录，校正结果满足基线校正的两条准则. 但是在选择速度末尾拟合时间段时主要与研究人员的经验有关，需要给出一个确定t1和t2的标准.

为了解决上述情况，Wu和Wu（2007）根据Boore（2001）的结果和处理强震动数据同震形变的经验（Wu et al., 2006a, 2006b），发现校正后的位移时程呈斜坡函数的形状. 建议选择地面从零位移开始移动的时间为t1，定义地面刚刚移动到永久位移位置的时间为t3， 并使用从t3到记录结束段的校正后位移时程确定“平坦度”f值：

式中，r为线性相关系数，b为校正后的位移时程从t3到 记录结束的最小二乘拟合直线的斜率. 将从t3到记录结束的校正后位移时程的平均值视为“永久位移”，并确定其方差 σ. 对于“良好”的强震动记录，t3之后的位移时程应该非常平坦. 因此，r的绝对值应该非常接近1，b应该接近0，并且σ 处于最小值. 在这种情况下，f值达到最大值. 将t2定义为从t3到记录结束之间的值，使用迭代的方法选择使校正后位移时程确定的f值最大对应的时间点作为最后的t2. Wu和Wu（2007）利用该改进的基线校正方法处理了1999年集集MW7.6地震和2003年成功MW6.8地震的近场强震动记录，并计算了永久位移，其结果与GPS测量的同震位移有很好的一致性. Akkar和Boore（2009）将vi=v0,i+af,it拟合到速度时程的tFITb=tFITe−i·Δ到拟合结束时间tFITe（tend）段，并绘制了连续斜率与tFITb的比值，选择这些比值达到相对恒定的时间为开始拟合时间tFITb. 将拟合直线与时间间隔(tFITb−i·Δ,tFITb) 的速度时程之间的标准差绘制为tFITb−i·Δ的函数，选择标准差突然增加对应的时间为基线结束时间tBLe. 将零阶校正速度时程与零线之间差异的标准差变化的时间定义为基线开始时间tBLb. 利用tBLe约束t2（t2≤tBLe） ，tBLb来 约束t1（t1≥tBLb）. Chao等（2010）简化了选取t1和t2的迭代过程，根据式（8）计算出加速度记录的能量分布比，利用加速度记录中能量分布的两个临界比值25%和65%来选择t1和t2，自动确定基线校正的时间点，避免了人工选择带来的主观性. 然而，该能量分布比是基于2003年成功MW6.8地震有限数量记录的经验值，而不是来自不同地震的大量记录，可能并不适用于其他地震.

式中，np是 P波到时的点，nc是t1和t2对应能量比的点. Wang等（2011）提出了一种改进的自动基线校正方法，首先确定t1和t2的选取范围，然后利用网格搜索法选择能用阶梯函数最佳拟合校正后的位移时程的时间为t1和t2，避免了选择时间的主观性.Lin等（2018）基于Iwan等（1985）方法提出一种基于目标最终位移的基线校正方法，与传统的基线校正方法是为了消除或最小化强震动记录的基线偏移不同，其目的主要是为跨断层桥梁结构提供在合理范围内的最终位移作为跨断层地震激发，用于检查跨断层桥梁在不同水平相对最终位移下的非线性地震特性或损坏模式，服务于跨断层的桥梁抗震设计. 熊政辉等（2019）运用加入L1范数正则化的最优化思想，以拟合速度误差尽可能小为目标并以加速度基线偏移稀疏为约束条件，通过凸优化技术多次迭代求解，可以自动识别出加速度记录中的单段式、两段式和多段式基线偏移，并计算其偏移时刻和偏移程度，减少了加速度基线校正中人为干预选择的主观性，拓展了基线校正方法的通用性. 赵思程等（2019）验证了典型的Iwan两段式校正方法、BAP方法和基于L1范数优化的基线校正方法对加入两段式和三段式噪声模型加速度记录的处理结果，并利用计算机视觉技术的地面运动测量系统获取的运动位移观测结果进行对比，结果表明基于L1范数优化的基线校正方法能更好地识别不同地震记录中基线偏移的起始时间以及偏移程度，减小了主观随机性. Tian等（2019）基于非倾斜二维振动台测试的观察结果，开发了一种具有累积校正模式的基线校正程序，并引入倾斜校正模式扩展了基线校正程序以处理3-D强震动，倾斜校正模式用于消除由于永久地面倾斜引起的积分速度的线性偏移. 累积校正模式用于消除由于系统误差以及倾斜校正模式未捕获的倾斜引起的累积速度偏移.

张斌等（2020）利用直线（10）拟合位移时程的t1～tend段，引入参数“时移斜率比ki”来确定强震段偏移开始时间t1，如式（11），选取未校正位移最后零交叉时间td0和tPGA中的较大值作为结束段开始拟合时间t3，然后以迭代的方式和校正后位移的最大平坦度确定结束段偏移的开始时间t2，如式（7）. 引入参数“均方根偏差RMSD”，如式（12），根据二次函数和三次函数分别拟合t2～tend段位移时程得到的RMSD最小来选择拟合函数的次数，避免对结束段偏移的错误校正.

基于Iwan等（1985）两段式校正方法原理发展的基线校正方法朝着半自动和自动校正处理方向发展，进一步减小了确定t1和t2时主观经验的作用，是从近场强震动记录恢复永久位移常用的基线校正方法.

2.4 基于小波变换的方法

Chanerley和Alexander（2010）提出了一种新颖的基于小波的算法，旨在校正基线偏移和倾斜并整合到位移中. 他们使用了1999年集集MW7.6地震和2008年冰岛MW6.3地震的强震动记录，表明一旦时程经过小波变换和去噪，垂直分量的长周期部分根据Graizer（2005）中方程（1）的条件积分为几乎完美的永久位移. 考虑到各自的信号噪声比（Chanerley et al., 2009），由于倾斜的影响，水平分量虽然也成功校正，但是显示出明显的位移偏差. 在所有事件中，他们的部分方法要求在记录的开始和结束时最小化速度.

3 结 论

本文首先阐述了导致近场强震动记录基线偏移的主要原因是低频误差和地面的倾斜或旋转，详细地分析了低频误差和地面的倾斜或旋转对于原始加速度记录积分获得的速度和位移时程的具体影响.讨论了近场强震动记录基线校正的原则. 针对近场强震动记录中存在的低频误差，论述了减少近场强震动记录中长周期噪声应用最广泛的高通滤波方法的基本原理，讨论了滤波器的选择、非因果滤波的加零填充、余弦渐变平滑零填充部分和加速度记录的过渡带、非因果滤波截止频率的选取标准以及去除零填充后如何避免获得的速度、位移和加速度反应谱值不兼容的问题. 针对地面倾斜或旋转引起的基线偏移，论述了Iwan等（1985）两段式基线校正方法的原理，以及基于Iwan方法原理开发和改进的基线校正方法的研究进展. 获得如下结论：

（1）低频误差和地面倾斜或旋转导致的基线偏移普遍存在于近场强震动记录中，在数据使用前对原始加速度记录进行高通滤波或基线校正非常必要，是获得稳定可靠的地震动参数和永久位移的基础. 对于大震近场的强震动记录，需要从加速度记录中获取对高层或超高层建筑、大跨桥梁、管道等工程的抗震设计非常重要的可靠长周期地震动信息和永久位移信息，需采用单段式或多段式基线校正方法进行处理. 对于小震的近场强震动记录，采用了高通滤波方法进行处理是最有效和最不主观的.

（2）目前常用的滤波器中，Butterworth滤波器的稳定性最好；非因果滤波在滤波过程中不会造成信号产生任何相位失真；进行非因果滤波前在加速度记录首尾添加相同长度的零填充可以避免加速度积分得到的位移时程中出现偏移和尾部翘起的情况；使用的余弦渐变函数可以平滑零填充部分和记录两端之间的过渡带；借鉴Boore（2012）在非因果滤波和去除零填充后进行后处理避免从加零填充数据和去除零填充数据积分获得的速度、位移时程和加速度反应谱值的不兼容. 严格的截止频率选取标准可以将高通截止频率选取的主观性降至最低，大大增强了数据处理结果的可靠性.

（3）基于Iwan方法原理开发和改进的基线校正方法朝着半自动和自动校正处理方向发展，进一步减小了确定t1和t2时主观经验的作用，是从大震近场强震动记录恢复永久位移常用的基线校正方法.

然而，目前还没有方法可以量化不同误差来源的贡献，以及还不能测量强震动记录的三个旋转 分 量（Graizer, 1979; Nigbor, 1994; Trifunac and Todorovska, 2001），已有这些基线校正方法大多是针对特定的一个或几个地震的强震动记录的经验方法，并没有适用于大部分地震近场强震动记录的通用基线校正方法. 随着全球范围内近场强震动数据的累积、目前大数据分析和机器学习等技术手段的日趋成熟，利用大数据分析和机器学习等技术手段，基于Iwan方法原理，从海量的近场强震动记录中自动快速地识别出稳定、可靠的校正时间点t1和t2将是未来发展方向.

附中文参考文献

胡聿贤. 2006. 地震工程学[M]. 北京：地震出版社.

彭小波. 2011. 汶川地震强震动记录分析及应用[D]. 哈尔滨：中国地震局工程力学研究所.

王国权，周锡元. 2004. 921台湾集集地震近断层强震记录的基线校正[J]. 地震地质，26（1）：1-14.

熊政辉，李小军，戴志军，陈苏. 2019. 基于L1范数正则化的强震动加速度记录基线漂移识别方法[J]. 地震学报，41（1）：111-123.

于海英，江汶乡，解全才，等. 2009. 近场数字强震仪记录误差分析与零线校正方法[J]. 地震工程与工程振动，29（6）：1-12.

张斌，俞言祥，肖亮. 2020. 近断层强震记录基线校正的改进方法[J].振动与冲击，39（5）：137-142.

赵思程，陈苏，李小军. 2019. 基于视觉观测技术的强震动记录校正方法验证[J]. 地震工程与工程振动，39（5）：189-198.