基于高阶异构度的执行体动态调度算法

贾洪勇，潘云飞，刘文贺，曾俊杰，张建辉

（1.郑州大学网络空间安全学院，河南 郑州 450001；2.国家数字交换系统工程技术研究中心，河南 郑州 450001）

0 引言

针对当今网络安全易攻难守的局面，美国国家科学技术委员会提出了移动目标防御（MTD，moving target defense）[1]。其采用包括IP 地址和端口跳变[2]、IP 安全协议随机化[3]、用户角色随机化、地址空间随机化[4-7]、指令集合随机化[8]以及动态路由[9]等相关技术手段构建一种动态的、不确定的网络攻防环境，使防御目标对攻击者表现出不可预测的状态。

2014 年，邬江兴院士[10]提出了网络空间拟态防御（CMD，cyber mimic defense），并结合生物学“拟态伪装”和“特异和非特异性免疫”现象，以异构冗余和动态反馈机制不断调整防御系统执行环境，从而打破以往的被动防御，以一种主动变迁[11]的方式对已知或未知漏洞后门等实现优秀的防御效果。其核心架构是动态异构冗余（DHR，dynamic heterogeneous redundancy）[12-13]，如图1 所示。

图1 DHR 架构

调度和裁决模块是DHR 的2 个核心模块。调度模块具有从等待池调度执行体进入运行池的功能，一个优秀的调度算法应兼顾调度的动态性和安全性，使攻击者无法判断当前运行执行体编号并使调入执行体对攻击者的攻击造成严重阻碍；裁决模块具有判断运行池中执行体输出是否正确的功能，其能帮助系统分辨出已被攻破的执行体，评估并预警系统的安全隐患。调度/裁决算法的可靠程度关系到DHR 架构的安全性，即整个系统的安全程度，因此对调度/裁决算法的研究是至关重要的。本文主要针对调度算法的优化进行研究。

目前，围绕调度算法[14]的优化问题，已有很多学者提出了相应的解决方案。文献[15]提出了基于历史信息的人工调度算法FAWA（feedback artificial weighted algorithm），该算法通过历史记录威胁信息动态调度执行体以达到动态改变的效果，但未考虑执行体间的差异性问题；文献[16-17]采用二阶相似性进行裁决/调度算法优化，这种方法能有效增大运行池中执行体的异构度，减小共模漏洞，但在等待池中执行体确定的情况下会造成执行体集调度单一化的问题；文献[18]提出了基于随机种子的调度算法，该算法考虑了调度的动态性和执行体间异构度，但其只考虑了执行体的二阶异构度，无法准确评估执行体间的差异性；文献[19]提出了高阶异构度的性质并给出了基于高阶异构度的裁决算法，其证明了引入高阶异构度的裁决算法具有优于传统仅考虑二阶异构度算法的安全性，但并未给出高阶异构度的计算方法。目前，执行体调度领域的研究缺少一种从高阶层面考虑执行体间异构度的动态调度算法。

本文的主要研究工作及贡献如下。

1)在FAWA 的基础上引入高阶异构度思想，设计并提出了一种同时考虑历史威胁信息和执行体高阶异构度的调度算法HFAWA（high level heterogeneity feedback artificial weighted algorithm），解决了因未考虑异构度导致系统共模漏洞过多、只考虑异构度造成执行体调度固化无法动态变动的问题。

2)基于容斥原理给出高阶相似度和高阶异构度的计算方式，解决了目前缺少高阶异构度计算方法的问题。

3)通过对DHR 结构中调度模块与裁决模块间关联分析，提出了根据裁决算法动态改变的HFAWA 改进策略，并以大数裁决算法为例给出了相应改变方法。

4)通过进行碰撞实验和大数裁决系统攻击（LSA，large number adjudication system attack）实验，对现有5 种调度方案进行对比评估，验证了HFAWA 相较于以往方案具有明显的安全性优势且兼具动态调度执行体的能力。

1 基于高阶异构度的负反馈调度算法

1.1 二阶异构度存在的问题

目前，在引入异构度的执行体调度算法的研究中，使用的异构度指标均为二阶异构度[16]，其通过异构体之间两两比较的差异程度值求和的方式来计算整体的差异度。当运行池大小大于2 时，仅考虑二阶异构度的调度算法会产生局限性，造成系统出现共模漏洞。下面进行举例分析。

假设在系统等待池中存在4 个执行体（编号为1～4），其存在的漏洞情况如表1 所示。

表1 执行体存在的漏洞情况

若当前所需调度执行体数量为3，则可以得到异构体间的2 阶相似度矩阵为

对各种调度情况的相似度进行求和，如表2所示。

表2 二阶相似度求和

算法应选取二阶相似度最小（即异构度最大）结果作为调度方案，即1，2，3 或1，3，4。但当观察执行体漏洞情况时发现，无论是1，2，3 还是1，3，4 均存在大小为1 的共模漏洞（5 或1）；当系统选择1，2，4 时，系统整体共模漏洞为0，为最优解。因此，需要引入高阶异构度来解决这一问题。

1.2 基于相似度的高阶异构度计算方法

文献[18]给出了二阶相似度的相关含义指标，即在余度为n的n模冗余体集合Ω中，相似度由集合中所有不同元素两两之间的相似度之和归一化表示，即

这种相似度计算方式缺乏对高阶异构性的考虑，没有分析高阶共生漏洞对异构体的影响，因此文献[19]提出了高阶相似度的相关含义，并给出了相关性质和推论。本节将在其基础上通过对容斥原理加以分析，从而提出高阶相似性的计算方式，并延伸至高阶异构度的计算。

容斥原理是统计学中一种常用的计数方法，在计数时为了防止重叠部分被重复计算，提出先对整体所有元素进行计数，然后排除被重复计算元素的方法。其数学表达式为

在碰撞实验中，执行体由防御原子组成，因此可以将执行体的防御面积当作该执行体中防御原子的集合，从而通过容斥原理计算多个执行体的共同防御面积，即相似性，如图2 所示。

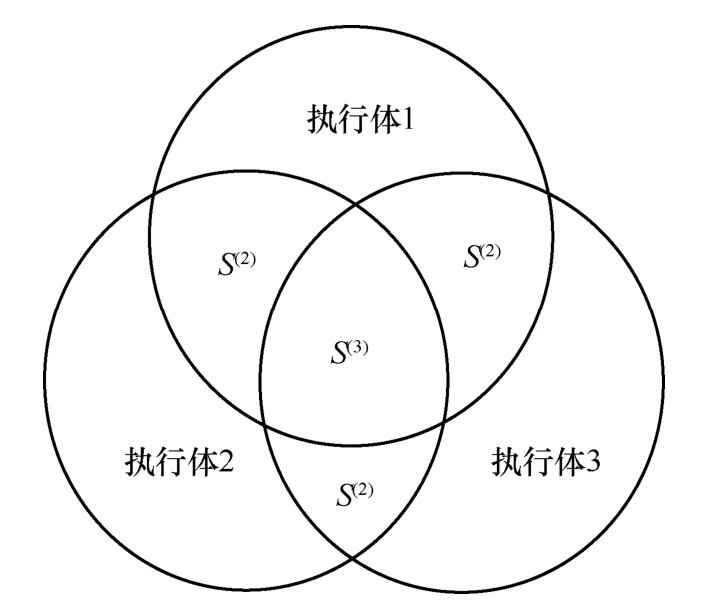
图2 三模异构冗余体的高阶相似度

图2中以圆的面积表示执行体的防御平面，S(2)表示2 个执行体之间的二阶相似区域，S(3)表示3 个执行体之间的三阶相似区域，同理，S(n)表示n个执行体之间的n阶相似区域，它们之间的关系为

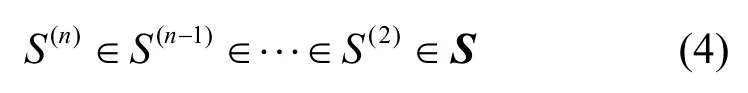
易知n阶相似区域性质与n阶相似度性质相符，因此，可将图2中的n阶相似区域等价为n阶相似度进行计算。

定义1高阶相似度计算方式。n模异构冗余体的防御面积为P(n)=|A1∪A2∪…∪An|，|Ai|=S（1）(1≤i≤N)|，|Ai∩Aj|=S(2)(1≤i＜j≤N)，…，|A1∩A2∩…∩An|=S(n)，则n模相似度计算式为

在得到高阶相似度S(n)之后，可进行计算求得高阶异构度[20-22]。以碰撞实验为例，高阶异构度的计算式为

对其进行归一化处理，有

1.3 算法内容

针对之前所述调度算法存在的问题，基于FAWA和高阶异构度思想，设计了一种同时考虑历史威胁信息和异构体间高阶异构度的动态调度算法HFAWA。符号表示如表3 所示，并根据以下定义对算法进行形式化描述。

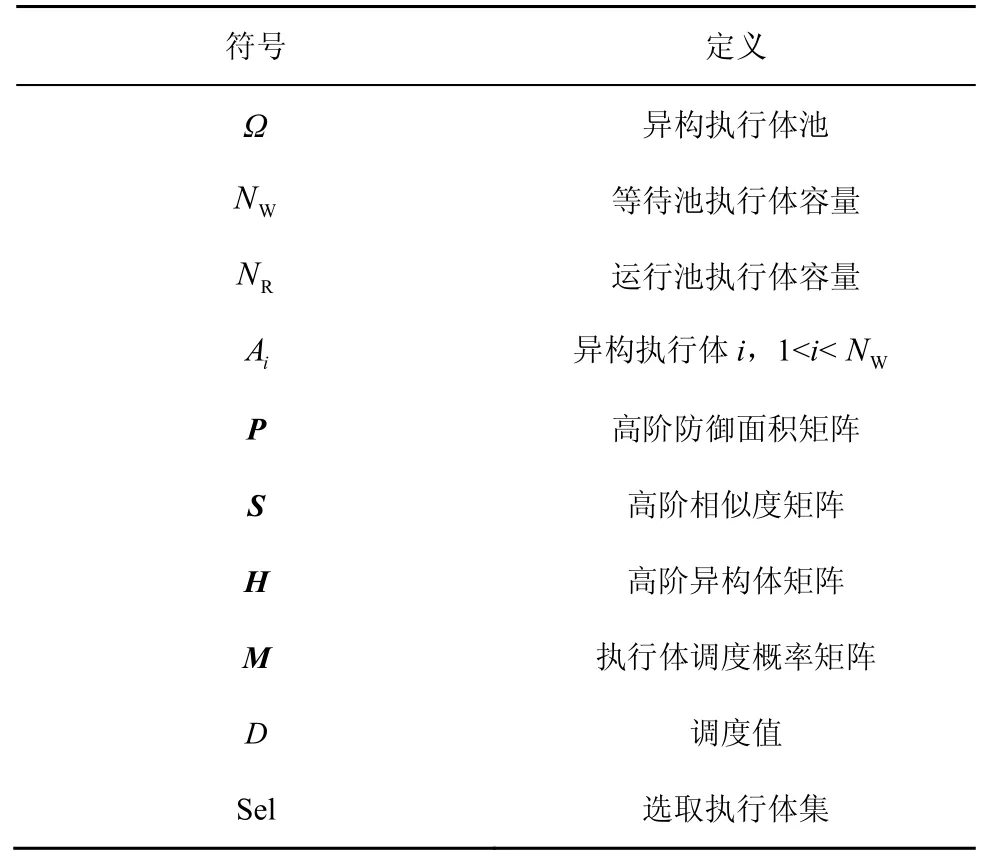
表3 符号表示

定义2异构执行体池。异构执行体池由多个功能等价的异构执行体组成，异构执行体池分为等待池ΩW和运行池ΩR，可表示为Ω={A1，A2，…，AN}，各执行体间相互独立。

根据表3中的符号定义，对其中部分符号的用法及计算方式做以下说明。

技术因素与技术团队的建设互为影响，技术选型影响着开发团队的技术组成和技术积累，同时团队现有的技术积累和人员配置又影响着技术选型。企业在做移动应用时，通常需同时考虑用户对应用的功能性和非功能性需求指标, 而非单纯的技术因素，下面对一些影响选型的限制因素进行分析。

4)M为执行体调度概率矩阵，其值根据历史威胁反馈动态改变，计算方式与文献[14]中计算方法相同。

5)调度值D是算法选取执行体的重要凭证，D值越大，执行体被调度的可能性越高。D的计算式为

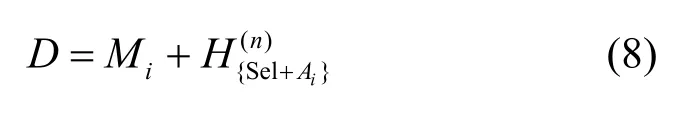
根据以上定义及计算式，基于高阶异构度的负反馈调度算法HFAWA 如算法1 所示。

算法1基于高阶异构度的负反馈调度算法HFAWA

输入等待池ΩW，运行池执行体容量NR，高阶异构度矩阵H，执行体调度概率矩阵M，选取执行体集Sel，最大调度值集合best_s。其中H(n)已提前计算完毕，M矩阵初始默认值为全1，Sel 与best_s 初始为空，大小与ΩR相同

输出运行池ΩR

算法1 为一次调度的HFAWA 实现，其中矩阵M随每次调度记录的历史威胁信息反馈而改变，从而影响下次调度结果。算法1 对应的算法流程如图3 所示。

图3 算法1 对应的算法流程

1.4 算法用例

下面以NR=5的DHR 系统为例，对HFAWA运行流程进行简要说明。

1)当选择执行体集Sel 为空时，挑选M数组中最大的执行体A1进行调度加入Sel。Sel={A1}，将Sel 送入算法进行下一执行体选择。

3)将等待池中除Sel中已有执行体外的执行体wi轮流与Sel中执行体匹配，计算选择D最大的执行体加入Sel；若D最大值不唯一，将对应执行体分别加入Sel。Sel={A1，A2，A3}，将Sel 送入算法进行下一执行体选择。

4)将等待池中除Sel中已有执行体外的执行体wi轮流与Sel中执行体匹配，计算M[i]，选择D最大的执行体加入Sel；若D最大值不唯一，将对应执行体分别加入 Sel。Sel={A1，A2，A3，A4}，将Sel 送入算法进行下一执行体选择。

5)将等待池中除Sel中已有执行体外的执行体wi轮流与 Sel中执行体匹配，计算D=，选择D最大的执行体加入Sel；若D最大值不唯一，从中随机选取一执行体加入Sel。S el={A1，A2，A3，A4，A5}，将Sel 输出，Sel 即当次选择调度5 模异构体。

1.5 算法分析

目前，针对多执行体策略的评估方法有很多，如基于博弈模型对攻防双方进行收益量化作为评判标准[23]、采用攻击成功累计时长作为评判标准[24]、采用成功控守目标个数作为评判标准[25]等。本文采用当前运行池中执行体集的共模漏洞个数作为评判标准。

在不考虑执行体历史信息的影响，即执行体调度概率矩阵M时。算法的调度值仅受异构度值Hi影响，即

以表1中执行体情况为例进行分析。

1)在算法初始选择执行体时，由于各执行体间无调度值差别，因此遍历所有执行体分别加入执行体待选集Sel中，并送入算法进行下一阶段执行体选择，Sel={{1}，{ 2}，{3 }，{ 4}}。

2)根据之前送入的执行体待选集，分别遍历剩余执行体并计算二阶异构度，选出异构度最高的集合送入算法进行下一阶段执行体选择。根据表1中执行体的二阶相似度矩阵可知，此时被选择送入算法的执行体集为Sel={{1，2}，{1，3}，{1，4}，{ 2，3}，{ 3，4}}（相似度最低）。

3)根据之前送入的执行体待选集，分别遍历剩余执行体并计算三阶异构度，选出异构度最高的集合，此时算法计算最高阶数与运行池容量相等，因此输出算法最终选择结果Sel={1，2，4}，共模漏洞数量为0。

算法中影响调度值的另一部分矩阵M仅受执行体的历史信息影响，即执行体被攻击次数。而在实际情况中，攻击者是无法预先探知拟态系统中被调度执行体的种类的，即攻击者的攻击意图与调度算法无关。因此，矩阵M对不同算法的安全性影响是相同的，而又由于增加了历史信息的影响，算法的动态性得到了提升（通过攻击者的攻击倾向而动态调度执行体）。

由此可见，HFAWA 在调度时会尽可能选择使系统共模漏洞数量少的执行体进行调度，能够在保证安全性的前提下表现出良好的动态性。

2 算法及实验改进

在碰撞实验中给出高阶异构度计算式H(n)=P(n)-S(n)，这样做的目的是尽量增大防御面积，选择防御面积最大的执行体集进行调度。但在实际的拟态场景中并非防御面积越大效果越好。在经典拟态场景中通常需要构建执行体池，由调度算法调度执行体进入运行池，最后根据裁决算法对执行体输出结果进行裁决。因此，一个优秀的调度算法往往需要根据拟态构造的裁决机制进行相应的调整。

目前，学者已提出了很多裁决算法，如基于高阶异构度的裁决算法[19]、基于二进制文件的裁决算法[26]、基于异常值的裁决算法[27]、大数裁决算法[28]等。相较于其他算法，大数裁决算法以其通用性被更广泛地应用于现有的DHR 系统中，其基本思想是将执行体输出相同数量最多的结果作为判决结果。因此本节将以大数裁决算法为例，对HFAWA 进行调整，同时构建相应测试模型对算法有效性进行测试。

本文在算法1和文献[15]碰撞实验的基础上做如下调整。

1)将碰撞实验中执行体由防御原子组成改为执行体由漏洞原子组成，每个执行体的漏洞原子个数为最大威胁数的，且最小不少于10 个。

2)威胁生成策略不变，为随机装载和全装载。碰撞测试调整为若执行体中存在威胁集中的漏洞原子则被攻破。在5 模异构执行体集中，若攻破执行体数超过3 个，则判断系统被攻破。

大数裁决下5 模执行体高阶异构度如表4 所示。调整后的实验算法如算法2 所示。

算法2大数裁决系统攻击实验算法

输入系统执行体池Ω，执行体调度概率矩阵M，调度总轮次n，历史威胁记录矩阵HS

输出系统平均攻破率PA

1)计算系统高阶异构度矩阵H，计算式如表4 所示

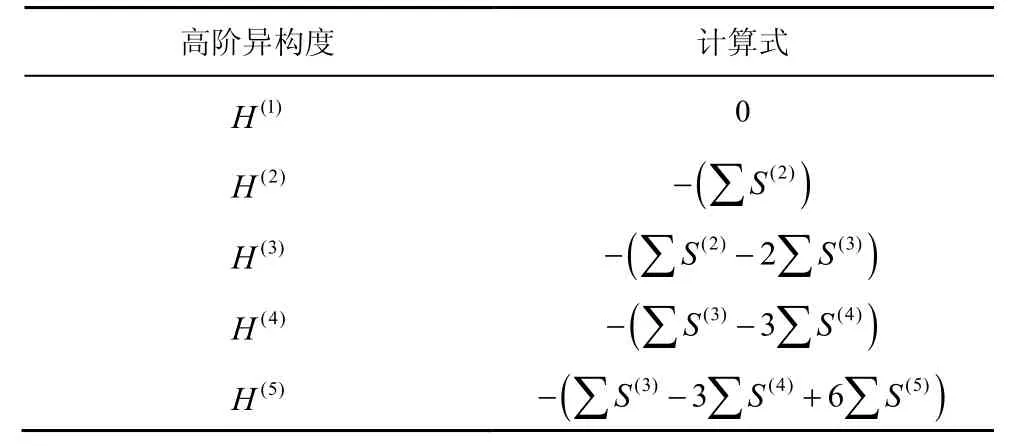
表4 大数裁决下5 模执行体高阶异构度

算法2 对应的实验流程如图4 所示。

图4 算法2 对应的实验流程

3 失效率分析

采用大数裁决算法的拟态防御系统被攻破的概率等效于运行池中半数以上执行体产生共模漏洞的概率之和，因此可以采用被选中的异构执行体共模漏洞的面积与公共漏洞的面积之比作为系统被攻破的概率。

几个基本假设如下。

假设1攻击者每次随机使用一种攻击方式进行攻击，若该攻击方式能同时攻破半数以上处于运行池中的执行体，则拟态系统被攻破。

假设2HFAWA、FAWA、H2 算法[15]均使用执行体的历史信息作为部分调度依据，虽然具体使用方法有所差异，但为了便于分析，均使用P(HI)表示被执行体历史信息（HI，history information）所影响的执行体调度概率。

假设3当前等待池中执行体的漏洞数量为，二阶共模漏洞数量为Nb，…，n阶共模漏洞数量为。漏洞总数为Nsum=Na∪Nb∪…∪Nz。

根据以上假设，可得各算法在运行池大小为k的拟态系统中的失效率如表5 所示。

表5 各算法在运行池大小为k 的拟态系统中的失效率

接下来，将通过实验比较以上算法的安全性能。

4 实验验证

4.1 安全性实验

为了验证HFAWA 的有效性，将其与其他4 种调度算法（FAWA、FIFO、Random、H2）进行对比。其中H2 为文献[16]中的算法，该文提出将异构度（2 阶）与历史信息（执行体运行次数）结合，其焦点在于裁决算法的改进，因此根据其思想实现“H2 调度算法”与本文算法进行对比分析。

本文通过2 种实验对算法的安全性进行对比，实验分别为碰撞实验和大数裁决系统攻击实验。其中碰撞实验由文献[14]提出，其核心思想是通过对攻击原子和防御原子的碰撞率来衡量系统的安全性，碰撞率越高系统越安全，实验步骤如下。

Step1等待池和运行池初始化。

Step2构造威胁输入。

Step3进行动态调度，从等待池中选取异构执行体填入运行池。

Step4进行碰撞检测和计数。

Step5返回Step2，重复进行多次实验。

Step6计算平均碰撞概率。

Step7改变威胁数目，返回Step1。

本文对碰撞实验进行改进，提出了LSA，实验流程如图4 所示。2 种实验的对比实验环境如表6所示。

表6 对比实验环境

表6中，随机部分装载与随机全装载均为随机装载，区别在于部分装载的执行体组成原子中可能会存在0 原子（无效原子）；全装载的执行体组成原子均为非0 原子（有效原子）。威胁构造方式分为负反馈和随机装载2 种，区别在于随机装载为随机选取攻击原子进行装载，而负反馈装载会选取之前的系统攻击结果中攻破概率最高的攻击原子进行装载。

仿真中相关实验参数设定如下。

1)执行体调度为5 模异构执行体集，即每次从等待池中调度5 个执行体到运行池中。

2)执行体的防御/漏洞原子、威胁集均为随机生成。

3)实验采用蒙特卡罗方法进行测试，每种实验环境下测试10 000 次，最后取均值表示实验结果。

4)负反馈威胁实验中威胁原子更新概率式与文献[15]中相同，为

其中，P1和P2在碰撞实验中分别表示发生碰撞和未发生碰撞的威胁原子被选中的概率，在LSA 实验中分别表示未攻破系统和攻破系统的威胁原子被选中的概率；p为单次实验中该威胁原子与防御/漏洞原子发生碰撞的概率。

实验参数配置如表7 所示。

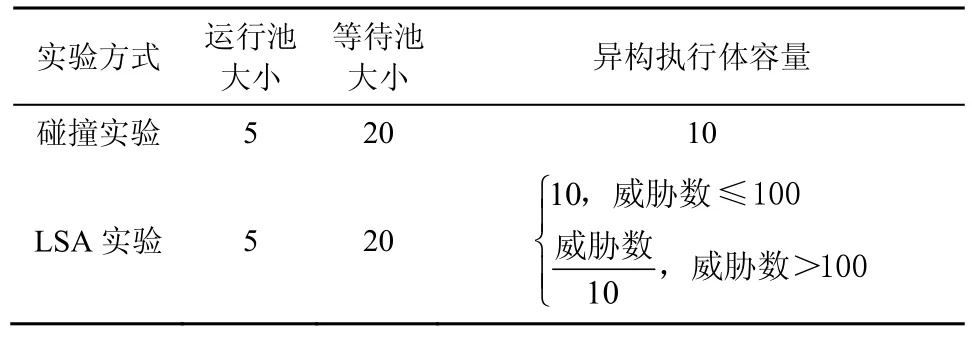
表7 实验参数配置

本文实验假设每次从等待池中调度5 个执行体（其中原子种类随机生成）进入运行池中工作，因此设定运行池大小为5，等待池大小为20。在碰撞实验中异构执行体容量参考文献[15]中参数进行设置；在LSA 实验中由于执行体中原子为漏洞原子，在通常漏洞发现的过程中，单一类型系统/软件存在的漏洞数量应与同功能的系统/软件发现的漏洞数量总数存在比例关系。因此在LSA实验中，当威胁数大于100 时异构执行体容量设定为，其执行体容量变化如图5 所示。实验结构如图6 所示。

图5 LSA 实验执行体容量变化

图6 实验结构

实验程序用Python 编写。为更好地量化实验结果，碰撞实验中用碰撞率表示威胁被系统防御的概率，碰撞率越高，代表系统防御能力越强；LSA 实验中用系统攻破率表示系统被威胁攻破的概率，系统攻破率越低，代表系统越安全。

4.1.1 碰撞实验

根据表5中的环境描述，在碰撞实验中分别测试了执行体负反馈威胁下部分装载、负反馈威胁下全装载、随机威胁下部分装载和随机威胁下全装载4 种环境，得到的实验结果如图7和图8所示。

从图7和图8 的实验结果可以看出，在全装载和部分装载的环境下，HFAWA 都具有优于其他算法的防御效果，且这种优势在威胁数较少时更明显。而攻击方式的改变会对系统的安全性产生一定威胁，但这种威胁主要体现在威胁数较少时碰撞率会有些许降低，威胁数较大时负反馈攻击的碰撞率反而高于随机攻击的碰撞率，这与文献[15]中的结论是一致的。

图7 碰撞实验下执行体全装载

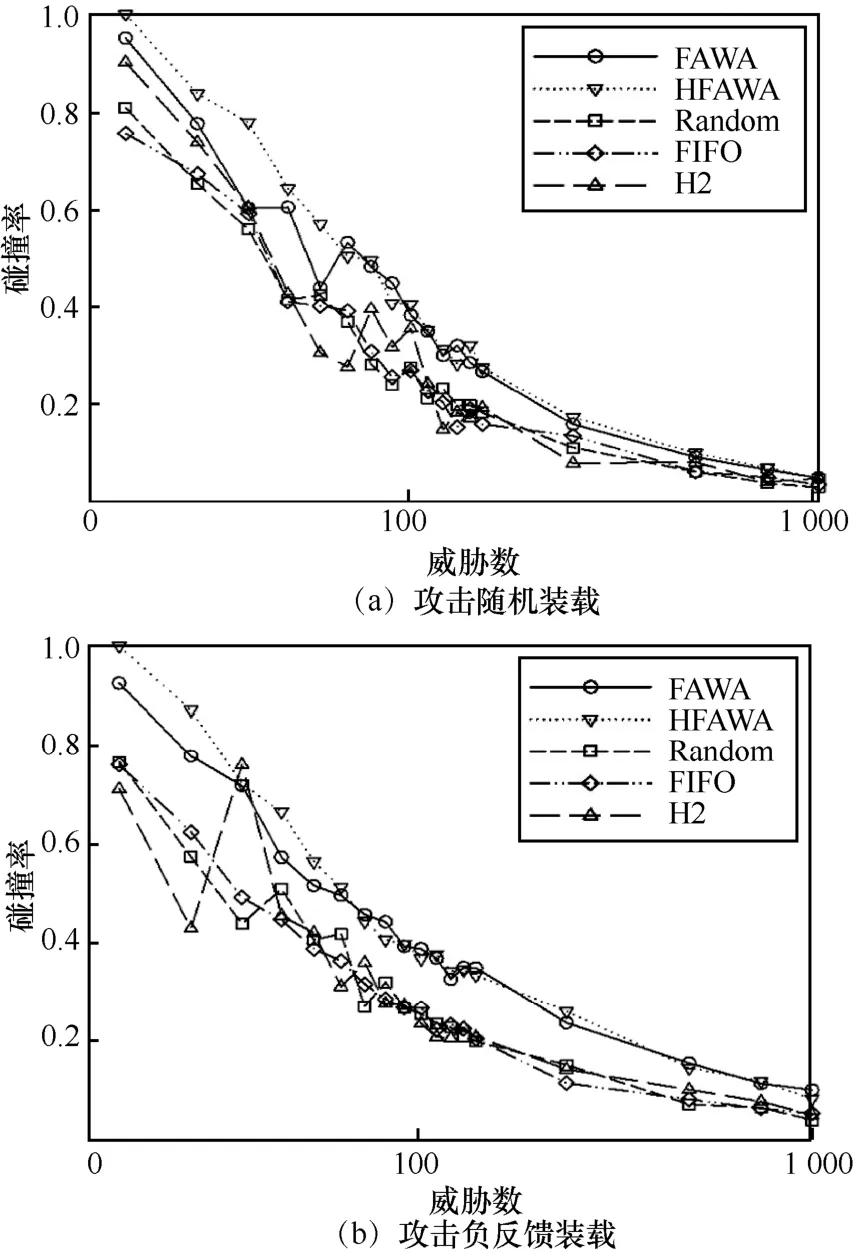
图8 碰撞实验下执行体部分装载

由于在实际场景中，异构执行体间虽然拥有相同的层级数，但其具有的防御能力和漏洞类型/个数往往都是不同的，因此部分装载的实验环境更能体现实际场景中的效果。给出部分装载环境下的详细实验数据，如表8和表9 所示。

表8 随机攻击碰撞试验下执行体部分装载实验结果

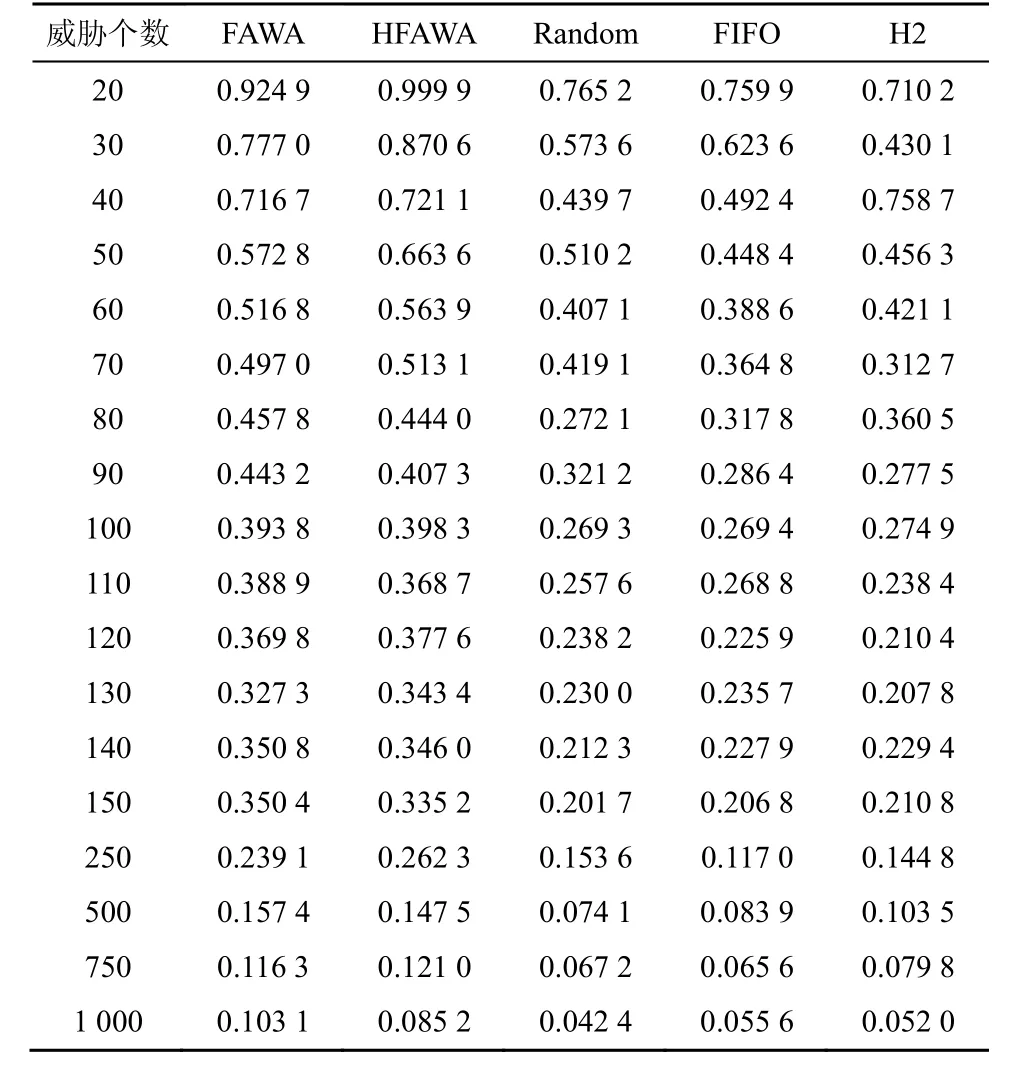
表9 负反馈攻击碰撞试验下执行体部分装载实验结果

4.1.2 LSA 实验

根据图4 所示流程进行实验，LSA 实验中同样测试了表5中描述的4 种环境，得到的实验结果如图9和图10 所示。

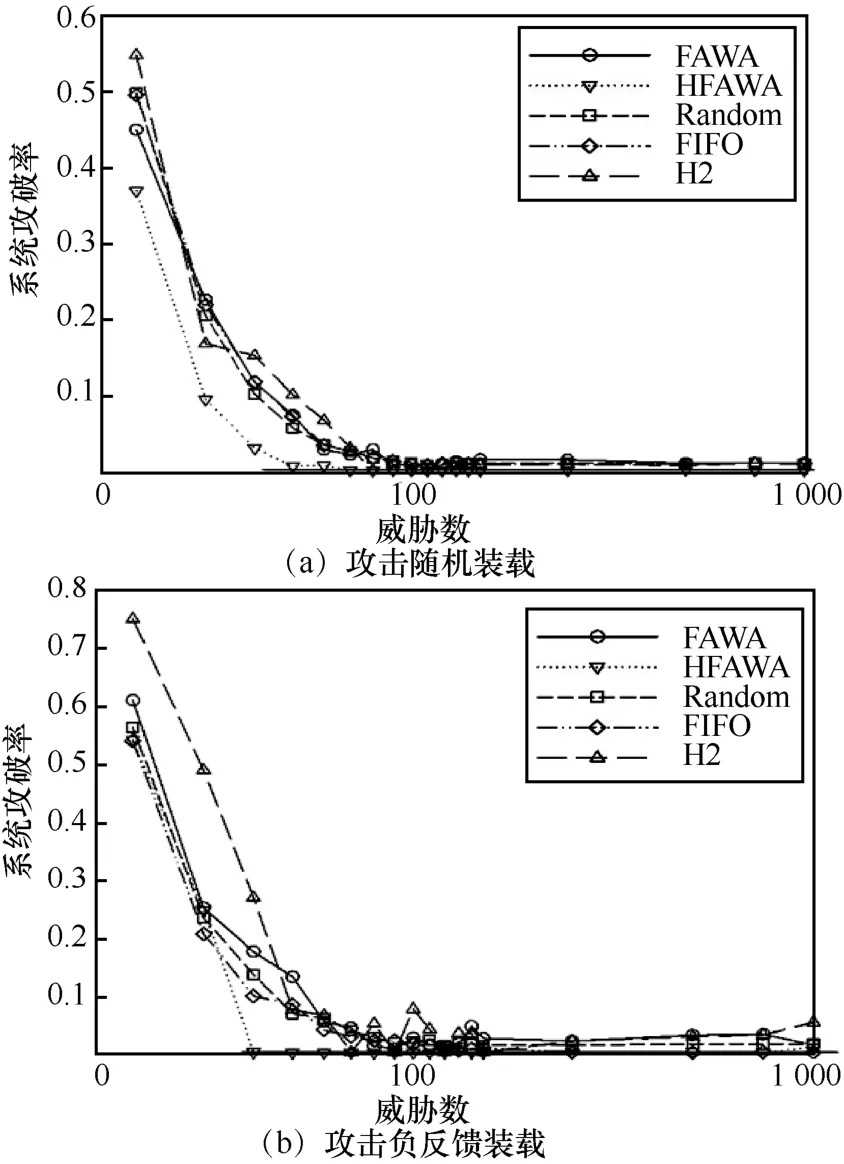
图9 LSA 实验下执行体全装载

图10 LSA 实验下执行体部分装载

从图9和图10 的实验结果可以看出，在LSA实验中，HFAWA 依然保持着良好的防御能力。虽然在攻击方式由随机攻击变为负反馈攻击后，系统攻破率会有些许上升，但通过对比可以看出，受影响较大的是威胁数较少的情况（H2 算法受到的影响最大），随着威胁数增大，攻击方式的改变对系统攻破率的影响可以忽略。给出部分装载实验的详细数据，如表10和表11 所示。

表10 随机攻击大数裁决下执行体部分装载实验结果

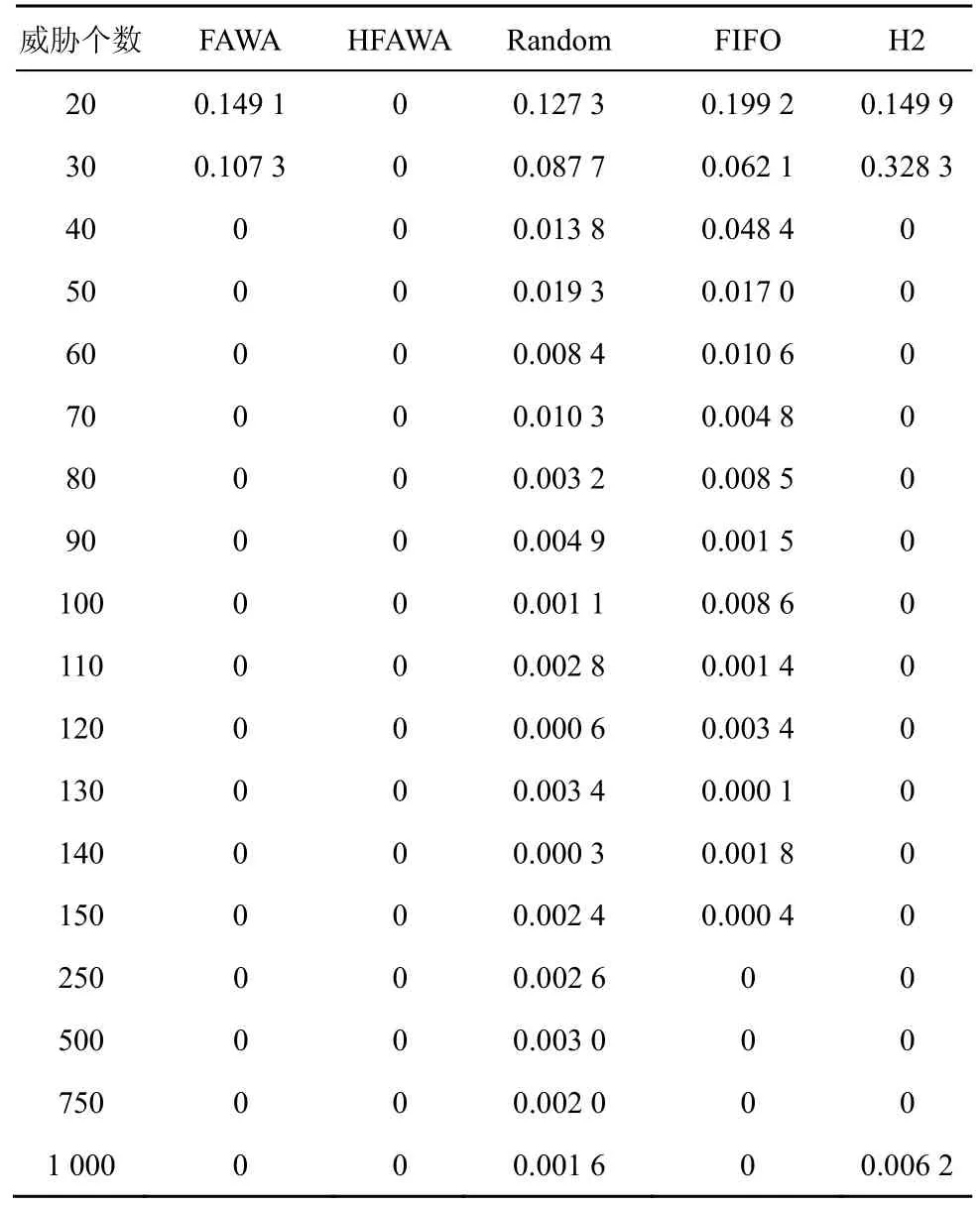
表11 负反馈攻击大数裁决下执行体部分装载实验结果

4.2 算法性能测试

根据以上实验参数配置，本文对5 种调度算法的运行时间进行仿真实验，实验环境如表12 所示。

表12 性能测试环境

实验只测试算法在调度选择过程的时间消耗，由于HFAWA、H2 算法中异构度数组的构建为前期准备工作，因此不将其算作算法时间消耗内。实验测试每种算法调度10 000 次的时间消耗，详细数据如表13 所示。

表13 算法时间消耗

在笛卡尔坐标系中绘制表13 所示实验数据，如图11 所示。

图11 算法时间消耗

根据以上实验结果，可以得到以下结论。

1)在碰撞实验中，HFAWA 的碰撞率基本上高于其他算法。当威胁数较小时，HFAWA 优势较明显；当威胁数大时，HFAWA和FAWA 的碰撞率相近且高于其他算法。这是因为威胁数越大，异构体选择防御原子相同的概率就越小。当威胁数趋近于无穷时，异构体间出现相同防御原子的概率为0，这时HFAWA 与FAWA 效果相同。

2)在LSA 实验中，HFAWA 的系统攻破率始终低于其他算法。在异构体部分装载环境下，使用HFAWA 的系统被攻破概率为0。这是因为在异构体部分装载环境下，5 模执行体中极易存在3模相似度为0（异构度最大）的情况，这时根据高阶异构度调度执行体的HFAWA 效果明显优于其他算法。

3)由算法性能测试结果可明显看出，HFAWA在威胁数少的情况下相较于其他3 种算法运行速度较慢，而较H2 算法更快。这是由于HFAWA 的时间消耗主要是算法中异构度数组的比较，这与运行池的大小有直接关系，与威胁个数关系不大，当威胁个数较大时这一消耗可以忽略。而相较于H2 算法中每次实验都需要更新的历史信息为二维数组，HFAWA 仅需对一维数组进行更新，因此HFAWA具有优于H2 算法的运行效率。

将以上实验算法的防御能力和运行速度指标进行对比，结果如表14 所示。

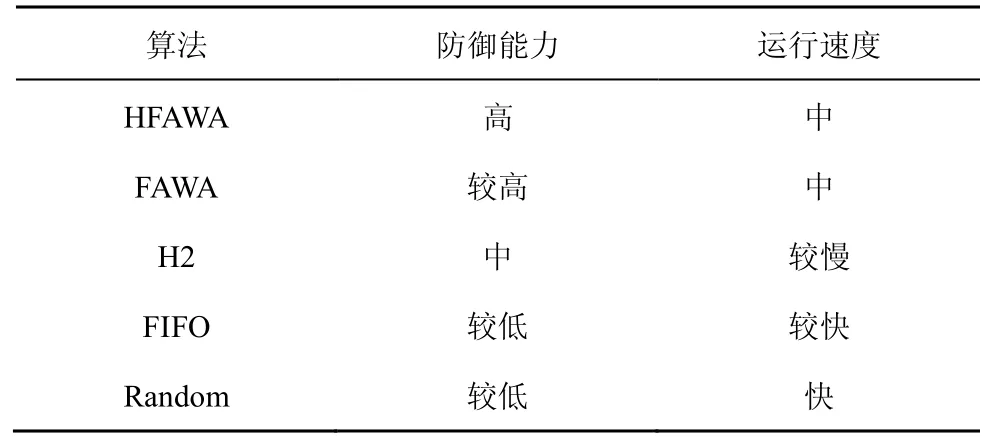
表14 算法指标对比

综上，HFAWA 能够在保证系统安全的同时，不造成过高的系统开销。

5 结束语

针对目前DHR 系统对异构度的考虑仅局限于二阶层面，造成系统安全性不足且调度异构体缺乏动态性的问题。本文提出了HFAWA 调度算法，并通过对容斥原理进行扩展应用，给出了高阶异构度的计算方式。仿真实验验证了HFAWA 具有良好的防御能力和运行速度。后续将基于本文所做工作，继续优化执行体的调度算法，进一步提高系统安全性。