可证明安全的抗量子两服务器口令认证密钥交换协议

尹安琪，郭渊博，汪定，曲彤洲，陈琳

（1.信息工程大学密码工程学院，河南 郑州 450001；2.南开大学网络空间安全学院，天津 300350；3.南开大学天津市网络与数据安全技术重点实验室，天津 300350）

0 引言

口令认证密钥交换协议的通信方只需要使用低熵口令就可以在非安全信道上协商用于安全通信的高熵密钥[1]。与其他认证方式相比，口令认证可以避免使用公钥基础设施（PKI，public key infrastructure）和涉及个人隐私的生物特征，有效提高安全系统在部署上的低成本性和便利性[2]。

然而，当前口令泄露问题日益突出，如很多网站都发生过客户口令泄露问题，且口令泄露在短期内往往难以被发现，如Yahoo 时隔4 年才发现其泄露了30 亿客户口令，这进一步加剧了口令泄露的危害。另一方面，基于传统困难问题（如大整数分解、离散对数）的密码体制无法抵抗量子算法的攻击[3]，且量子计算技术飞速发展，特别是商用量子计算机已经诞生[4]，因此基于传统困难问题的口令认证密钥交换（PAKE，password-authenticated key exchange）协议在量子时代将不再安全。

格密码体制是典型的抗量子密码体制，因其在计算上具有高效性、在困难实例选取上实现了随机性[5]且在全同态加密等领域应用前景广泛[6]，被认为是最有潜力的后量子密码体制之一。但格上PAKE 协议的研究起步较晚且投入较少。如目前格上的PAKE 协议多为单服务器设置，此类方案在单个服务器上存储了客户的认证信息（如口令或口令的哈希值）；一旦该服务器泄露，认证信息将全部泄露，即此类协议存在口令泄露问题。

两/多服务器认证是抵御服务器泄露攻击的有效方式，但基于格困难问题的此类研究相当有限。在基于传统困难问题的PAKE 协议领域，相关方案可分为基于PKI 模型[7-8]、基于身份（ID，identity）[9-10]和唯口令[11]3 种。但只有唯口令方案符合PAKE 协议的设计初衷，即允许客户在只拥有低熵口令的前提下实现认证。其他2 种方案分别需要客户管理系统公钥和服务器身份等信息。相比之下，目前在格上只存在个别基于PKI 模型的多服务器口令认证密钥传输协议[6]，且不能应用于两服务器场景。虽然在格上实例化ID2S 架构[10]是实现抗量子两服务器PAKE 协议的可行技术路线，但只能得到基于ID 的密钥传输方案，即上述2 种基于格的方案虽然宣称是PAKE 协议，但实际上都只实现了密钥传输。

此外，格上的PAKE 协议目前还不能很好地发挥格密码体制的线性计算优势。主要原因之一是现有方案一般需要使用签名/验签[12-13]、零知识证明[14-15]等密码原语来保证安全性。而格上的多服务器PAKE 方案[6]进一步需要使用全同态加密、秘密共享等密码原语。这些昂贵密码原语的使用降低了协议的执行效率，且增加了通信与存储开销。

据本文分析，实现格上高效的两服务器PAKE协议主要有三点挑战。1)实现唯口令设置和密钥交换。一方面要使客户不需要存储和管理系统公钥、服务器身份等信息，从而提高安全系统的可部署性；另一方面要实现密钥交换而不局限于密钥传输。2)避免使用签名/验签、全同态加密、零知识证明和秘密共享等昂贵密码原语，并降低协议通信轮次，以精简协议架构进而降低协议开销和简化协议的安全性分析。3)设计格上IND-CCA2 安全的两方平滑投影哈希函数（SPHF，smooth projective hash function），同时约束基于的公钥加密（PKE，public key encryption）方案中相关参数的大小，以消除带误差学习（LWE，learning with error）问题不完全同态性对SPHF 正确性的影响。该类SPHF 是构建唯口令两服务器PAKE 协议的有效数学工具[11，16]，但据本文所知，目前还没有基于格的两方SPHF，且此前即使是格上的集中式SPHF 最多也只能保证不可区分性选择密文攻击（IND-CCA1，indistinguishability under chosen-ciphertext attack）的安全性。

因此，本文主要研究格上IND-CCA2 安全的两方SPHF，以解决现有分布式SPHF 无法抵抗量子攻击和现有格上SPHF 安全性不高的问题，并进一步提出格上可证明安全的唯口令两服务器PAKE 协议，以抵抗服务器泄露、量子攻击，同时解决现有格上相关方案可部署性差且执行效率低的问题。实验结果表明，与其他相关方案相比，所提出的SPHF和PAKE 协议具有较高的执行效率。

1 相关工作

在基于传统困难问题的PAKE 协议领域，文献[17]首次给出了唯口令的方案，这使PAKE 协议的研究不再局限于PKI 模型。早期PAKE 协议的开销一般很大，甚至不具备实用性。文献[18]在2001 年提出了第一个高效的PAKE 架构称为KOY 架构。此后，为降低协议各方面的开销，协议的通信轮次不断降低，协议架构由最初的三轮（KOY[18]/GL[19]和JG[20]/GK[21]架构）发展到两轮[22]以及一轮[23]架构。但上述方案都是单服务器方案，无法抵御服务器泄露攻击。为此，两/多服务器PAKE 协议应运而生。文献[9-10]虽然宣称提出了基于身份的通用两服务器PAKE 协议架构，即可以基于任何两方PAKE 方案实现两服务器PAKE 协议，但实际上只能实现密钥传输。文献[11]基于秘密共享技术，提出了一种唯口令的门限PAKE 协议。但一般情况下，多服务器PAKE 协议不能用于两服务器场景，反之亦然。

与基于传统困难问题的PAKE 协议相比，格上PAKE 协议的研究起步较晚。文献[24]在2009 年才在KOY 架构下提出了第一个格上的PAKE 协议。文献[15]基于非交互式零知识证明技术，在2017 年给出了格上第一个两轮PAKE 协议。直到2018 年，文献[14]才提出了第一个格上的一轮PAKE 协议，但该协议需要使用零知识证明、签名/验签以及平滑性放大等技术来保证IND-CCA2 安全性，这导致协议的计算、存储和通信开销较大。文献[12]改进了文献[14]中的一轮PAKE协议，虽提高了效率却仍无法避免签名/验签算法的使用。与上述基于格的单服务器PAKE 协议相比，格上两/多服务器PAKE 协议的研究更加不足。文献[6]宣称提出了格上第一个多服务器PAKE 协议，但该方案实际上只实现了密钥传输，并没有实现密钥交换；该方案基于PKI 模型，且需要多次使用全同态加密、签名/验签、零知识证明、秘密共享等技术来保证安全性，开销较大。虽然可以在格上实例化通用的ID2S 协议架构[9-10]，但只能得到基于ID 的密钥传输方案，无法实现唯口令认证和密钥交换，且该架构无法避免签名/验签算法的使用，而基于格的签名/验签算法一般具有较大的算法参数，这会进一步增大协议开销。

SPHF 是构建PAKE 协议的有效数学工具，但SPHF 的应用不局限于该领域，其在零知识证明、不经意传输以及证据加密等领域[14]都具有相当广泛的应用。SPHF（实际上是精确SPHF）的概念最初由文献[25]提出。由于在格上构建精确SPHF 比较困难[26]，文献[24]首次提出了一种基于格的近似SPHF，并利用纠错码技术，仅基于该近似SPHF 实现了格上的第一个PAKE 协议。随后，文献[14-15]基于上述技术路线，提出了基于不同格上PKE 方案的近似SPHF。文献[27]提出了一种格上IND-CCA1 安全的公钥加密算法，一般称为MP 公钥加密算法，由于其执行效率较高，因此成为格PAKE 领域应用最广泛的公钥加密算法之一。文献[28]则基于MP 公钥加密算法[28]提出了一种格上的精确SPHF，但由于算法参数较大，计算开销成倍提高。

SPHF 可分为适应性[24]与非适应性[14]两类。在非适应性SPHF中，投影密钥的计算不需要使用密文，因而此类SPHF 成为构建低轮次（特别是一轮）PAKE 协议的有效数学工具[14]。目前，格上的非适应性SPHF 只能保证IND-CCA1或不可区分性选择明文攻击（IND-CPA，indistinguishability under chosen-plaintext attack）的安全性[13]。虽然个别文献[14]基于带标签的IND-CCA2 安全的PKE 方案设计了非适应性SPHF，但由于要求标签固定，该SPHF 只能保证IND-CPA 安全。

此外，根据计算参与方的数量多少SPHF 又可以分为集中式和分布式两类。在基于传统困难问题的SPHF 领域，文献[11]提出了一种基于DDH 假设的分布式SPHF，但无法抵御量子攻击，也不适用于两方计算场景。文献[16]实际上隐式地给出了一种两方SPHF，也无法抵抗量子攻击。据本文所知，目前格上还不存在分布式（包括两方）SPHF。

本文工作借鉴文献[29-30]的研究思路展开，主要贡献总结如下。

1)基于LWE 问题的加法同态属性，提出了一种格上IND-CCA2 安全的非适应性两方SPHF，支持一轮两方PAKE 协议的构造。由于LWE 问题的不完全同态性会影响SPHF 的正确性，本文还约束了所基于的PKE 方案中相关参数的大小。

2)基于所提出的两方SPHF，在被动和主动敌手的攻击下，分别提出了基于格的两服务器PAKE协议，以抵抗量子和服务器泄露攻击。所提出的2 个协议都是唯口令设置，且不需要使用签名/验签、全同态加密、秘密共享等密码原语，被动敌手攻击下的协议还避免了零知识证明的使用，因而提高了安全系统的可部署性和效率。

3)在文献[13，16]中安全模型的基础上，给出了一种更加现实的两服务器PAKE 安全模型，该模型可以更加准确地评估PAKE 协议面临的真实风险。在所提出的更加现实的PAKE 安全模型下，严格证明了本文2 个协议的安全性。证明基于标准模型，从而避免了随机预言机的使用。对于PAKE 协议而言，使用随机预言机不仅存在实际应用中被一般哈希函数替代而导致的安全隐患，还可能造成PAKE协议遭受离线口令猜测攻击。

2 预备知识

在介绍本文所需的预备知识之前，首先给出本文必要的符号说明，如表1 所示。

2.1 基于格困难问题的公钥加密算法

格。设矩阵A∈ℝm×n，且A的列向量线性无关，另设格用Λ表示，并定义格Λ为

其中，A为格Λ的基矩阵，m为格Λ的维数，t为上的随机向量。

判定性LWE（dLWEn，m，q，χ）问题。设m，n，q，u为正整数，其中m≥n，q≥2，m=poly(n)，q≤2poly(n)。另设正整数e为dLWEn，m，q，χ问题误差，且e的概率分布为χ。dLWEn，m，q，χ问题定义为区分以下分布的问题：1)At，χ=(a，u=＜t，a＞+e)，其中

误差分布。设w为随机向量，并设概率密度函数ρs，c(w)=exp(-π||w-c||2/s2)。对于格Λ∈Zm×n，设。Λ上的离散高斯分布为

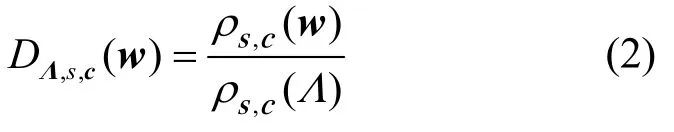
其中，向量c和变量s分别为离散高斯分布的中心和平滑参数。进一步地，若将DΛ，s，c(w)的定义域约束为，那么为截断离散高斯分布。由于截断离散高斯分布和离散高斯分布在统计上相近[24]，为便于描述，下文直接省略截断二字。本文中dLWEn，m，q，χ问题的误差分布χ为截断离散高斯分布。格上IND-CCA2 安全的公钥加密方案。在格上，一般利用IND-CPA 安全的PKE[31（]在随机预言机模型下）或IND-CCA1 安全的PKE（利用哈希证明、零知识证明、陷门或BCHK 等技术[32]）构建IND-CCA2安全的PKE。因此，目前基于格上PKE[28，33]构建的PAKE 协议需要使用额外的密码原语来保证IND-CCA2 安全性。上述BCHK 技术又分为基于签名和基于Mac 这2 种。文献[32]利用基于Mac 的BCHK 技术，提出了一种IND-CCA2 安全的PKE，本文将其记作ZYF。接下来介绍该方案。

设m，n，，k，κ为正整数，其中nlbd≥3κ，。设 (encoded，decoded)表示编/解码算法，F(2κ)表示阶为2κ的有限域，H:{0，1}*→ F(2κ)/{0}表示定义域为{0，1}*、值域为F(2κ)/{0}的抗碰撞哈希函数，FRD:F(2κ)→表示定义域为F(2κ)、值域为全秩差编码算法，KG和ENC 分别表示密钥生成算法和加密算法，那么ZYF方案的定义如下。

2.2 平滑投影哈希函数

设pw 为口令，D为口令空间，label 为有效标签，hash 为哈希函数，C和Cpk分别为与公钥pk 对应的密文和(label，C)对的集合。对给定的公钥pk，定义集合X和Lpw（pw∈D）分别为

一般称三元组 (label，C，pw)为单词，用W表示。根据X和Lpw的定义可知，L={Lpw}pw∈D⊂X。

现给出近似平滑投影哈希函数的概念[24]。令Ham 表示汉明距离函数，l表示哈希密钥长度，参数ε表示错误的比例；KH 表示哈希密钥，K表示KH 的集合；KP 表示投影密钥，S表示KP 的集合；HASH 表示定义域为X、值域为Zq的哈希函数；H表示关于HASH 的哈希函数簇；projKG 表示投影函数，其定义域为K，值域为S。近似平滑投影哈希函数定义为输入公钥pk和集合L、X，输出 (K，G，H={HASH(W，KH):X → {0，1}n}，S，projKG(KH):K → S)，且满足以下条件。

2)正确性。对于∀W=(label，C，pw)∈L，哈希值h=HASH(W，KH)可由投影密钥KP 确定。即存在一个函数projHASH，称为投影哈希函数，以投影密钥KP、W以及W∈L的证据r为输入，投影哈希值ph 为输出，且满足以下条件

3)平滑性。对于∀W=(label，C，pw)∈X/L，K和KP=projKG(KH)，以下2 个分布在统计上不可区分

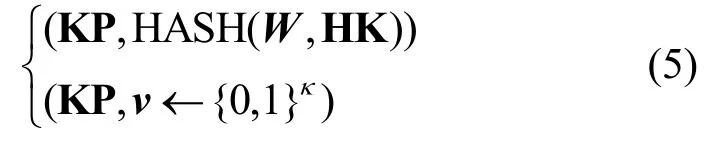
近似SPHF 只能实现近似正确性，文献[14]给出了通过纠错码算法实现正确性放大从而得到SPHF 的通用技术，接下来介绍该技术。

令{hashKG′，projKG′，HASH′，projHASH′}表示近似SPHF，其值域为{0，1}v；令ECC 表示纠错码算法，其可以纠正ε比例的错误。那么以下定义的{hashKG，projKG，HASH，projHASH}是SPHF。

由于上述技术可以直接将近似SPHF 转换为SPHF，为方便描述下文直接称近似平滑投影哈希函数为平滑投影哈希函数。

3 两服务器PAKE 安全模型

本节基于文献[13，16，34]中的模型，给出了一种更加现实的两服务器PAKE 安全模型，该模型能更加准确地评估PAKE 协议面临的真实风险。

3.1 通信模型

协议的参与方包括客户C∈Client，服务器A，B∈Sever和敌手/攻击者A ∈Adv。客户持有口令pwC，服务器A和B分别存储口令份额pwA，C和pwB，C，且满足pwA，C+pwB，C(modq)=pwC。一个服务器可以处理多个客户的认证请求，本文仅以一个客户为例，研究两服务器PAKE 协议。

在协议执行过程中存在“客户-服务器”之间和“服务器-服务器”之间的通信。本文假设敌手完全控制“客户-服务器”之间的通信，因此敌手可以窃听、注入、篡改、延迟或拦截该通信网络上的任何消息。服务器的存储空间相对充足，可以存储长期密钥等其他信息。因此，本文假设“服务器-服务器”之间的通信是安全的，即敌手无法窃听或控制未泄露服务器之间的通信。实际上可通过设置可信服务器来实现秘密信息的分发。此外，假设服务器与客户之间的通信是异步的；并假设服务器之间的通信是半同步的，即若客户向服务器端发送消息，各服务器可以在规定的时间间隔内收到该消息。

文献[34]提出的BPR 模型是应用最广泛的PAKE 安全模型之一。在BPR 模型中，每个参与方可以与其他参与方并行地执行多个协议。该模型用实例Π建模协议的执行，如表示客户C的第i个实例，表示服务器A的第jA个实例，且一个实例只能使用一次。每个实例，如，拥有一个状态变量。其中，表示实例的会话标识，它为接收和发送的消息统一编号，服务器之间的传输消息不计入在内；表示客户C认为的其通信伙伴的标识，在两服务器PAKE 协议中，对于客户C而言，是一个集合，即={A，B|A，B∈Sever}；表示会话密钥，同理；表示标识是否终止的二值变量，若终止，则=1，这表示完成了消息的发送和接收；表示标识是否被接收的二值变量，若实例最终被接收，那么=1，这表示成功终止。

3.2 敌手模型

本文假设敌手最多入侵某客户2 个认证服务器中的一个，并称被入侵的服务器为泄露服务器。本文将敌手分为被动和主动2 种类型。在被动敌手攻击下，泄露服务器仍按协议的定义执行，但敌手可以获得该服务器的内部状态信息。而主动敌手可以进一步控制泄露服务器向客户和相关服务器发送的消息。注意，在本文的通信模型下，被动敌手也可以控制服务器向客户发送的消息，但2 种敌手都无法窃听或控制2 个未泄露服务器之间的通信。

BPR 模型[34]用预言机建模敌手能力，敌手可以通过访问不同的预言机来执行不同的攻击。在BPR模型中，敌手与客户或服务器（实际上是客户或服务器的实例）之间的交互是通过访问预言机实现的。根据BPR和文献[16]中的安全模型，现将两服务器PAKE 协议中的敌手能力建模为以下预言机。

Execute(C，i，A，B，jA，jB)。该预言机建模离线口令猜测攻击，并根据协议的定义向敌手返回实例之间的传输信息。

以下Send 预言机建模在线口令猜测攻击，敌手可以向客户或服务器发送Send 预言机询问。

Send(C，i，(A，B)msg)。该预言机向实例发送消息msg，并根据协议的定义向敌手返回传输消息。特别地，Send(C，i，(A，B))可以启动客户C与服务器(A，B)之间的一次协议执行。

Send(A，jA，B，C，msg)。该预言机向实例发送消息msg，并根据协议的定义向敌手返回传输消息。特别地，若服务器A（或B）泄露，敌手可以额外获得A（或B）的内部状态信息。

Reveal(C，A，i)。该预言机（其中A∈pidC）建模会话密钥泄露攻击，如会话密钥的非法擦除等，并向敌手返回会话密钥。

在介绍Test预言机前，首先给出新鲜性的概念。

Test(C，A，i)。该预言机（其中A∈pidC）不建模任何真实的敌手能力，只用于定义安全协议。该预言机选择一个随机比特b，若b=1，其向敌手返回真实会话密钥；否则，其向敌手返回与等长的随机串。敌手只能执行一次Test(C，A，i)询问，且只能执行关于新鲜会话密钥的Test 询问。

在本文中，敌手仿冒某泄露服务器向相关服务器发送消息的行为也属于在线口令猜测攻击。

在主动敌手攻击下（不妨设服务器A泄露），任何协议无法保证正确性条件2)一定成立，但本文在第5.2 节提出的协议满足若=1，那么正确性条件3)一定成立。

敌手优势。口令认证密钥交换协议应该具备语义安全性，即敌手无法区分真实的会话密钥及与之等长的随机串。设敌手进行Test 询问后，给出的猜测比特为b′，若b′=b，称敌手成功，并记该事件为Success。定义敌手优势Adv(A)为

理想情况下，敌手成功的概率Pr(Success)的上限为+negl(κ)（negl(κ)为可忽略函数）。此时敌手优势Adv(A)的上限为negl(κ)。但由于客户实际使用的口令空间较小，敌手总能通过在线口令猜测成功，敌手优势的上限必定大于negl(κ)。因此，如果敌手所能执行的最佳攻击方式为在线口令猜测攻击，则称PAKE 协议是安全的。

设概率多项式时间（PPT，probabilistic polynomial time）的敌手执行在线攻击有次数上限，为Q(κ)。文献[11]在定义安全PAKE 协议时，一般假设口令服从均匀分布，此时敌手优势的上限为negl(κ)。但文献[35]的研究表明，口令服从均匀分布大大低估了敌手在线口令猜测的成功率，因而基于口令均匀分布假设的安全模型也大大低估了PAKE 协议面临的真实风险。因此，本节假设口令分布服从CDF-Zipf 定律[35]，并重新定义了文献[11]中的安全两服务器PAKE 协议。

定义1安全两服务器PAKE 协议。设PPT 敌手A执行在线口令猜测攻击的次数有上限，为Q(κ)；并设口令空间为D，且口令分布服从CDF-Zipf 定律。假设敌手最多入侵某客户2 个认证服务器中的一个，如果对于所有的PPT 敌手A，存在可忽略函数negl(κ)，满足

称协议Π 是安全的两服务器PAKE 协议，其中，C′=0.062 239和s′=0.155 478是CDF-Zipf 分布的拟合参数[13]，κ是安全参数。

根据文献[36]，基于CDF-Zipf 口令分布模型的敌手优势与真实敌手优势最多相差0.491%，且与基于口令均匀分布模型进行口令猜测相比，基于CDF-Zipf 口令分布模型进行口令猜测的成功率可提高2～3 倍。因此，所提出的两服务器PAKE 安全模型更加现实，其精确度可比基于口令均匀分布假设的安全模型提高2～3 倍。

4 格上的IND-CCA2 安全的两方SPHF

两方SPHF 是构建唯口令两服务器PAKE 协议的有效数学工具。但据本文所知在格上还不存在此类SPHF。在基于传统困难问题的SPHF 领域，可以通过集中式SPHF 构建两方SPHF，但这在格上比较困难，原因有三。一是目前格上的SPHF 多是近似SPHF，利用此类SPHF 设计的两方SPHF 不能满足正确性要求。二是虽然存在个别精确SPHF[27]，但一方面该SPHF 基于强LWE 问题，因而算法参数较大，执行效率成倍降低；另一方面，鉴于强LWE 问题也只具备不完全加法同态属性，直接利用该SPHF 构建的两方SPHF 仍不能满足正确性要求。三是现有的格上集中式SPHF 只具备IND-CPA 或IND-CCA1 安全性，基于这两类SPHF设计的两方SPHF 不能保证IND-CCA2 安全性。此外，为优化协议的通信轮次，本节研究非适应性SPHF。

本节利用LWE 问题的加法同态属性，基于ZYF 方案（见第2.1 节）研究格上IND-CCA2 安全的非适应性两方SPHF。

设ZYF方案的公钥为pkZ，公共本原矩阵为Gb，哈希密钥长度为κ。记本文提出的格上非适应性两方SPHF为WI-2SPHF，包括哈希密钥生成函数hashKG、投影函数proj、哈希函数HASH和投影哈希函数projHASH 这4 个子函数。WI-2SPHF (hashKG，proj，HASH，projHASH)的定义如下。

其中，RD(x)表示对x进行四舍五入操作。最后输出哈希值h:=(h1，…，hκ)。

由第2.2 节中SPHF 的定义可知，SPHF 要具备：1)正确性，即哈希值可通过哈希密钥或者投影密钥2 种途径计算，这保证协议双方可以协商一致的会话密钥；2)平滑性，当单词W∈X/L时，即使公开投影密钥，敌手也不能学习到哈希值的任何信息，这保证了SPHF 的安全性。下面证明本文提出的WI-2SPHF 是平滑投影哈希函数。

定理1WI-2SPHF 是平滑投影哈希函数。

证明 详见附录1。

5 格上可证明安全的两服务器PAKE 协议

在格上，PAKE 协议目前多为单服务器设置，无法抵抗服务器泄露攻击。个别可抵抗该类攻击的方案也只能实现密钥传输，且需要基于PKI 模型[6]，因而客户需要存储和管理系统公钥。虽然可以在格上实例化文献[9-10]中通用的ID2S 架构，但只能得到基于身份的两服务器密钥传输方案，导致客户需要额外存储和管理服务器身份等信息。因此，本节研究格上唯口令的两服务器PAKE 协议，以提高安全系统的可部署性。此外，为应对不同的性能和安全性需求，本节分别研究被动和主动敌手攻击下可证明安全的两服务器PAKE 协议。

5.1 针对被动敌手攻击的两服务器PAKE 协议

假设协议在客户C与服务器A、B之间执行，C持有口令pwC，A和B分别存储口令份额pwA，C和pwB，C，满足pwA，C+pwB，C(modq)=pwC。

基于所提出的WI-2SPHF，本节针对被动敌手攻击，提出了一种格上可证明安全的唯口令两服务器PAKE协议，记作2S-PAKE，如图1 所示。

协议所需的密码原语、初始化阶段及执行过程如下。

密码原语。1)格上IND-CCA2 安全的ZYF 方案；2)基于格的两方SPHF、WI-2SPHF。

初始化阶段。协议参与方（包括客户C与服务器A、B）在初始化阶段建立公共参考序列CRS=((A，B)，Gb)，其中pkZ=(A，B)和Gb分别是ZYF 方案的公钥和公共本原矩阵。

服务器A与服务器B的操作对称，下文仅以服务器A为例说明服务器端的操作。

本文通过证明定理 2，证明所提出的2S-PAKE 协议在第3 节中更现实的安全模型下是被动敌手攻击下安全的两服务器PAKE 协议。

定理2若ZYF 方案是IND-CCA2 安全的公钥加密方案，且WI-2SPHF 是平滑投影哈希函数，那么图1 所示的2S-PAKE 协议在被动敌手攻击下是安全的两服务器PAKE 协议。

证明协议的正确性与安全性证明见附录2。

5.2 针对主动敌手攻击的两服务器PAKE 协议

假设协议仍在客户C与服务器A、B之间执行。与针对被动敌手攻击的协议相比，针对主动敌手攻击的协议要求服务器A和B在运行ExeAB 协议时，向对方证明其本身正确使用了口令份额，本节使用证据不可区分协议实现此目标。

本节利用文献[37]中的证据不可区分协议Σ，改进图1中的ExeAB 协议，从而得到主动敌手攻击下安全的两服务器PAKE 协议。由于服务器A与服务器B的操作具有对称性，下文仅以服务器A为例说明ExeAB 协议的变化。

服务器A运行Σ协议，各参数设置如式(14)所示。服务器A同时作为验证者，根据协议Σ对服务器B进行验证，若验证失败，则结束协议的执行。

定理3若ZYF 方案是IND-CCA2 安全的公钥加密方案，且WI-2SPHF 是平滑投影哈希函数，那么经过上述改变后，图1 所示的2S-PAKE协议在主动敌手攻击下是安全的两服务器PAKE协议。

证明详见附录2。

6 协议仿真与性能分析

本节将所提出的WI-2SPHF和2S-PAKE 与其他相关方案进行对比。为实现公平对比，所有的仿真实验均使用Python 语言，统一在Intel(R)Core(TM)i5-4590 平台上进行，该目标平台的操作系统为Windows7，频率为3.3 GHz，内存为8 GB。

为方便进行各类开销的对比，本节假设κ=32 bit，m=800 bit，=416 bit，n=32 bit，n1=16 bit，n2=16 bit，q=4 096 bit。该参数规模符合第2.1 节中的参数设置要求。

6.1 格上平滑投影哈希函数的评估

本节首先对不同的SPHF 进行仿真，以得到相应的执行时间；然后从安全级别和仿真时间等方面对比评估所提出的WI-2SPHF。表2 给出了格上不同SPHF 的对比情况。

根据表2 可知，只有WI-2SPHF 具备INDCCA2 安全性。当哈希密钥长度大于128 bit 时，WI-2SPHF-1S 计算开销最小，且WI-2SPHF-2S 的计算总开销小于集中式的 KV.SPHF[24]和Reg.SPHF[12]；当哈希密钥长度为 512 bit 时，WI-2SPHF-1S 的计算开销比目前最优的MP.SPHF[13]提高了约27.6%。综上，本文方案具有高效性，这得益于本文的高效投影函数和两方SPHF 避免了额外密码原语的使用。而且随着会话密钥长度的增加，WI-2SPHF-1S 计算开销的增幅最小，即其密钥长度可扩展性较好。

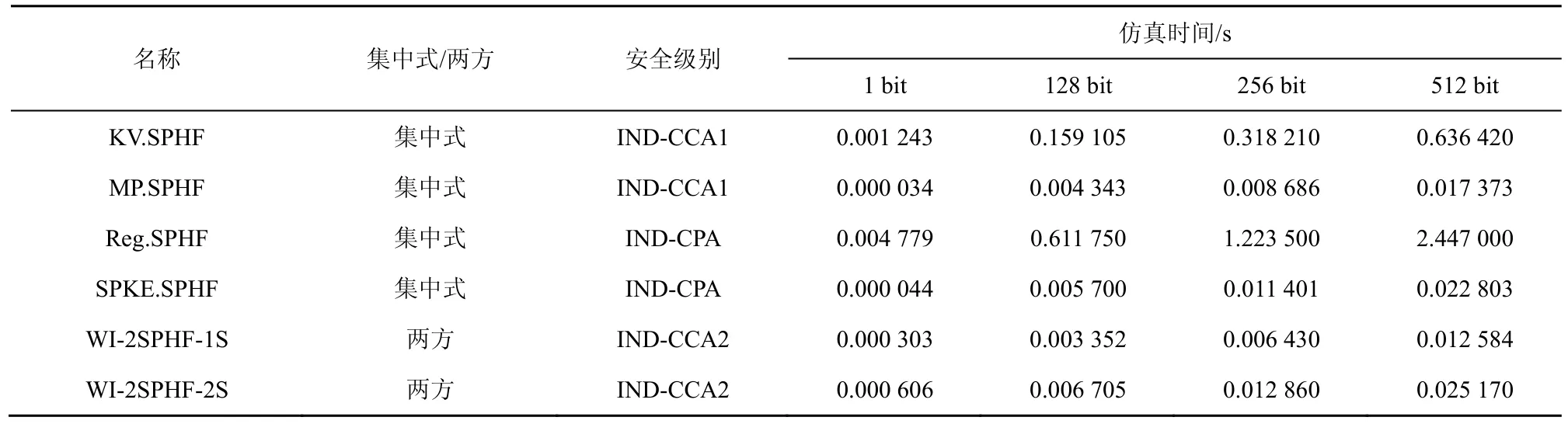
表2 格上不同SPHF 的对比

6.2 两服务器PAKE 协议的评估

本节首先仿真不同的协议，以得到相应的执行时间、存储空间占用量和通信数据量；然后从执行效率、存储与通信开销以及安全性等方面对比评估所提出的两服务器PAKE 协议。

据本文所知，Roy 协议[6]是目前格上唯一可抵抗服务器泄露攻击的相关方案。若假设Roy 协议是两服务器设置（实际上其不能用于两服务器场景），其需要调用5 次全同态加密、2 次零知识证明、8 次签名/验签、2 次加/解密算法和9 次矩阵运算，这对于资源受限的客户端而言，在很多应用场景中甚至不具备实用性。相比之下，在客户端，本文协议避免了全同态加密、零知识证明以及签名/验签算法的使用。在服务器端，本文协议在被动敌手攻击下进一步避免了秘密共享算法的使用，但所需的加/解密次数增加；在主动敌手攻击下，本文协议也需要使用零知识证明，但与Roy 协议相比仍具有高效性。然而，本文协议中矩阵运算的次数高于Roy 协议，这主要是因为本文协议是密钥交换协议，而Roy 协议只是密钥传输协议。

文献[6]的主要贡献是提出一种秘密共享方案，Roy 协议则是由该方案导出的，协议架构复杂，需要反复使用大量额外的密码原语来保证安全性，这导致Roy 协议的效率明显低于本文协议，且Roy协议仅是一种密钥传输方案，没有实现密钥交换。为进一步评估2S-PAKE 协议的性能，表3 给出了典型PAKE 协议架构下不同协议之间的性能对比情况，其中仿真时间是指协议执行的总时间。

根据表3可知，虽然2S-PAKE是两服务器方案，但执行效率依然高于除Li-Wang’s PAKE1 外的所有单服务器协议。若简单地将Li-Wang’s PAKE1 协议扩展为两服务器协议，其在服务器与客户端的仿真时间都为0.009 434 s，相比之下，2S-PAKE 在客户端和服务器端的仿真时间分别降低了 25.2%和15.1%。这说明了本文方案的高效性，这主要得益于本文高效的WI-2SPHF。

2S-PAKE 在客户与服务器间只需一轮通信，通信轮次最优，但其通信开销大于KV.PAKE 外的其他协议，这主要是两服务器认证所致。因Zhang-Yu’s PAKE和Li-Wang’s PAKE2 是两轮协议，其在通信时延上的优势小于其他协议。Katz et al.’s PAKE 的公钥长度较大，所以2S-PAKE 的存储开销明显较小；除此之外，本文协议的存储开销在客户端与服务器端分别是其他协议的1.12～2.05 倍和1.12～2.01 倍，这主要是两服务器认证和公钥长度较大所致。在实际应用时，本文协议在各开销上的劣势将会减小，因为其他协议的开销要在表3中数据的基础上添加由签名/验签等算法引入的额外部分。在主动敌手攻击下，本文协议在服务器端也需要额外计入由零知识证明带来的开销，因此性能有所下降。

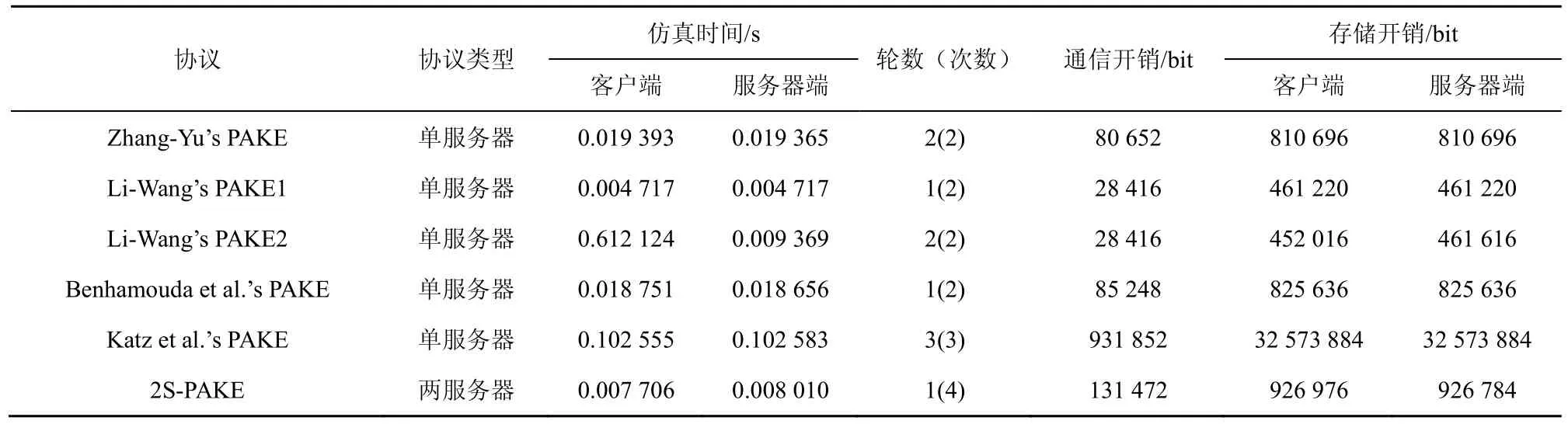
表3 典型PAKE 协议架构下不同协议之间的性能对比

表4 给出了不同协议的安全性及其他性能对比。其中轮数（次数）特指服务器与客户之间的通信轮次。轮数是指通信双方之间双向通信的数量，次数是指单向通信的数量。若是异步通信，二者相等；若是同步通信，后者是前者的两倍。

与Yi1[9]、Yi2[10]和Raimondo et al.’s PAKE[11]协议相比，本文协议和Roy 协议[6]基于格困难问题，可以抵抗量子攻击。而本文协议与Raimondo et al.’s PAKE 是唯口令的PAKE 协议，不需要基于PKI 模型（Roy 协议）与服务器身份（Yi1、Yi2 协议），因此这3 个协议所对应的安全系统具有更强的可部署性。本文协议与Yi1、Yi2 协议是两服务器认证协议，不适用于多服务器场景，而Roy、Raimondo et al.’s PAKE 协议是阈值方案，不适用于两服务器及服务器数目小于相应阈值的应用场景。

根据表4 可知，只有本文的2S-PAKE 协议在被动敌手攻击下不需要使用零知识证明与签名/验签等来保证安全性，提高了执行效率并降低了通信与存储开销。而在主动敌手攻击下，本文协议只需要在服务器端使用零知识证明。此外，Raimondo et al.’s PAKE和Roy 协议在每次执行时都需要多次使用秘密共享算法，这进一步增加了协议的开销。

表4 不同协议的安全性及其他性能对比

与密钥传输协议Yi1、Yi2和Roy 协议相比，本文协议和Raimondo et al.’s PAKE 协议可实现密钥交换，会话密钥由所有参与方协商而成，而不是由一方选定。此外，Yi1 与Yi2 协议是否需要使用随机预言机取决于所基于的密码原语，而Raimondo et al.’s PAKE、Roy和本文协议基于标准模型，直接避免了随机预言机的使用。随机预言机的安全性本身存疑，因为在实际应用中需要使用具体的哈希函数替代随机预言机；而对于PAKE 协议而言，使用随机预言机可能导致更加严重的安全威胁，因为这可能导致PAKE 协议遭受离线口令猜测攻击。

综上，本文提出的SPHF和PAKE 协议基于格困难问题，只需要采用矩阵、向量等线性运算，与传统困难问题（如大整数分解和离散对数问题）采用的模幂运算相比，在实现上具有高效性，且与传统困难问题相比，格困难问题具有最坏情况与平均情况下的安全性归约，因此本文协议在应用时可以随机选取困难实例，这大大提高了协议使用的便利性。此外，由于本文协议是唯口令设置，所对应的安全系统不需要硬件部署，也不涉及用户不可撤销的隐私泄露问题，可部署性强。

7 结束语

本文基于LWE 问题的加法同态属性，提出了一种格上IND-CCA2 安全的非适应性两方SPHF，可支持一轮两方PAKE 协议的构造。本文还约束了该SPHF 所基于的PKE中相关参数的大小，以消除LWE问题的不完全加法同态属性对SPHF正确性的影响，且该SPHF 具有相对独立的研究价值，可应用于证据加密、零知识证明和不经意传输等领域。

在此基础上，为抵抗量子和服务器泄露攻击，本文分别针对被动和主动敌手的攻击，提出了格上可证明安全的唯口令两服务器PAKE 协议，前者执行效率较高，后者安全性更高。本文提出的2 个协议在客户与服务器之间都只需要一轮通信，不需要使用签名/验签、全同态加密和秘密共享等昂贵的密码原语，被动敌手攻击下的协议还避免了零知识证明的使用，因此大大降低了计算、通信和存储开销。据本文所知，本文提出的SPHF和PAKE 协议分别是第一个基于格的两方SPHF和两服务器PAKE 协议。本文还在标准模型下，基于一种更加现实的两服务器PAKE 安全模型对本文的2 个协议进行了严格的安全性证明。实验结果表明，本文提出的两方SPHF和两服务器PAKE 协议执行效率较高。此外，在基于口令的安全方案中，口令更新是一个重要问题。但据本文所知，目前还不存在基于格的分布式口令更新方案，这也是下一步的研究方向。

附录1 WI-2SPHF 的正确性与平滑性证明

证明1)正确性证明

根据SPHF 的定义，要证明WI-2SPHF 的正确性，需要证明对于∀W=(label，(c1，c2，c3，c4)，pw)∈L，式(15)成立。

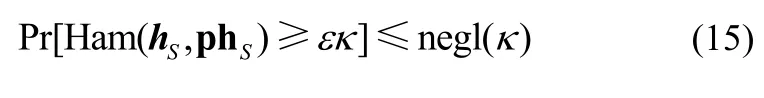
根据WI-2SPHF 的参数设置，要保证式(15)成立只要保证和满足SPHF 的正确性要求即可。

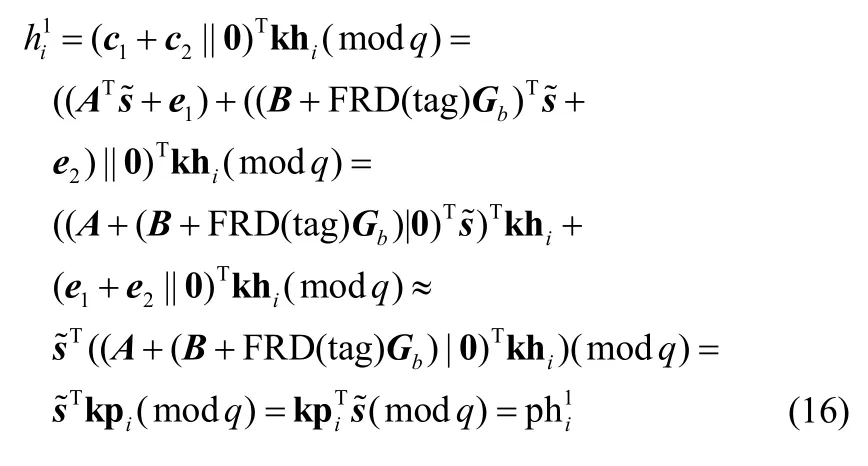
由式(16)可知，本文提出的WI-2SPHF 具备正确性。

2)平滑性证明平滑性要求即使投影密钥泄露，哈希值与随机数不可区分。首先证明对于∀W=(label，(c1，c2，c3，c4)，pw)∈X/L，式(17)中的2 个分布在统计上不可区分。

不妨设A泄露，本文构建模拟器Sim 为敌手模拟两方SPHF 的执行，且要求敌手无法区分真实的和模拟的两方SPHF。Sim 应该在已知(hA，phA，KPA)和WI-2SPHF 的输出(hS，phS，KPS)，但不知哈希密钥KHA和秘密s～A的前提下，成功模拟WI-2SPHF 的执行。

根据第4 节中WI-2SPHF 的定义，对于i∈[1，κ]，模拟器Sim 可以计算

根据式(18)可知，B在不知道A的哈希密钥KHA与秘密的前提下，可以正确计算投影密钥KPB、哈希值hB与投影哈希值phB。因此，本文提出的WI-2SPHF 是平滑的。

综上，定理1 成立。

证毕。

附录2 格上两服务器PAKE 协议的正确性与安全性证明

证明1)正确性证明

与被动敌手攻击下的协议相比，主动敌手攻击下的协议只改变了ExeAB，二者关于会话密钥的计算方式是等价的。因此，本文只给出被动敌手攻击下协议的正确性证明。

由式(20)可知图1 所示的2S-PAKE 是正确的。

2)安全性证明

①被动敌手攻击下协议的安全性证明

给定敌手A攻击协议，Sim 为A模拟协议的执行。下文假设A泄露，并对协议进行安全性证明。

Sim 首先执行初始化阶段，包括选择公共参数，为客户C选择口令pwC，并为A和B分发口令份额pwA，C和pwB，C（满足(pwA，C+pwB，C)modq=pwC）等。

本文通过一系列实验来评估A的优势，其中P0表示敌手与真实协议交互的实验。具体地，本文通过证明相邻2 个实验中的A的优势差是可忽略的和确定A在最后一个实验中的优势上限，来确定A在P0中的优势上限，从而证明协议的安全性。

实验P1。实验P1与P0的区别如下。

a)若发生以下情况，敌手不会成功，且实验中止：msgC发生了重复；由Sim 产生的msgA或msgB发生了重复。

b)将未泄露服务器B计算skA′的方式替换为skA′=projHASH(K PA，WC，A)⊕HASH(WA′，KHC，A)。

注意Sim 可以执行上述b)操作，因为此时是被动敌手攻击，b)操作所需的参数对于Sim 而言是已知的。

上述a)中情况发生的概率是可忽略的，因而其带来的敌手优势变化也是可忽略的。相对于实验P0，实验P1中skB′计算方式的改变只是概念上的，这种改变不会带来敌手优势的变化，所以

实验P2。改变skB′的计算方式，令其为一个随机数。利用标准的混合证明法，易知，只要ENC 加密方案是安全的，那么该变化引起的敌手优势变化是可忽略的，即

为方便证明，下文将msg 分为敌手产生的和预言机产生的两类。进一步，若敌手产生的msg 对应合法的口令，那么称该msg 为合法的，否则称其为非法的。假设模拟器Sim 生成的公私钥对为(pkZ，skZ)（相关定义见ZYF 方案），注意私钥skZ只在安全性证明中用于验证敌手生成的msg是否合法，而真实协议的执行并不需要私钥skZ。

根据以上证明可知

实验P4。若msgC由敌手产生且非法，将skB，C替换为随机数，同时将MB替换为随机数关于pkA的加密值。

根据平滑投影哈希函数的平滑性，并由msgC非法（WC，A∈X/L）可知，hA←HASH(WC，A，KHA)与随机数不可区分，所以skB，C=skB⊕skA′=hB⊕phB⊕skA′与随机数不可区分。同理MB的输入也与随机数不可区分。所以

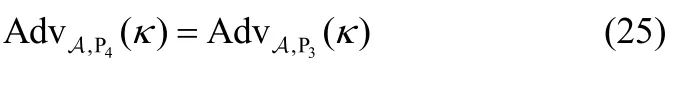
实验P5。若msgC由敌手产生且合法，那么直接宣布敌手成功；在其他情况下，敌手成功的定义不变。

该改变只会增加敌手的优势，所以

此时，若msgC由之前的预言机生成，那么若msgC由敌手产生且非法，那么skC，B与MB是随机的；若msgC由敌手产生且合法，那么敌手成功，且实验结束；若msgC重用，那么实验中止。

实验P6。服务器B改变其生成ZYF 密文的方式，用非法口令（口令服从CDF-Zipf 分布）的份额生成ZYF 的密文。

基于ZYF 方案的IND-CPA 安全性，利用标准的混合证明法，以及本文关于语义安全的定义易知

实验P7。若msgA与msgB由敌手产生且非法，改变msgA与msgB的回复方式，将skC，B和skC，A设置为随机数。

由于msgA非法，即WA∈X/L且WA′∈X/L，根据SPHF 的平滑性可知，HASH(WA，KHC，A)和HASH(WA′，KHC，A)都与随机数不可区分。根据图 1 进一步可知，在客户端哈希值hC，A←HASH(WA，KHC，A)⊕HASH(WB′，KHC，B)与哈希值hC，B←HASH(WB，KHC，B)⊕HASH(WA′，KHC，A)都与随机数不可区分，那么skC，A=hC，A⊕phC，A和skC，B=hC，B⊕phC，B也都与随机数不可区分。所以

实验P8。若msgA与msgB由敌手产生且合法，那么直接宣布敌手成功，并中止实验；在其他情况下，敌手成功的定义保持不变。该改变只能增加敌手的优势，所以

实验P9。改变服务器B关于ZYF 密文的生成方式，将其替换为非法口令（服从CDF-Zipf 分布）份额的加密值。

根据ZYF 方案的IND-CCA2 安全性，并利用标准的混合证明方法，易知

在实验P9中，除了敌手A知晓其生成了合法的msgC（msgA/msgB）的情况外，协议的执行与合法口令（口令份额）无关，这说明即使敌手A获得了泄露服务器A的口令份额pwA，C（pwA，C是Zq上的随机数），pwC也是安全的。此外，模拟器Sim 除了检验msgC（msgA/msgB）的合法性外，也不会使用合法的口令（口令份额）。

令GuessPW 表示以下事件：敌手发送了有效的msgC（msgA/msgB）。本文假设口令分布服从CDF-Zipf 定律，那么

这说明，虽然对于一个msgC而言，敌手A可以进行两次在线口令猜测，但是敌手A要想成功，需要将有效的msgC同时发送给服务器A和服务器B，因此敌手A实际上执行了两次在线口令猜测。

若敌手A未能猜测出合法的口令，那么敌手A只能通过Test 预言机询问获得成功，所以有

进一步，根据b的随机性可知，敌手A在实验P9中的优势满足

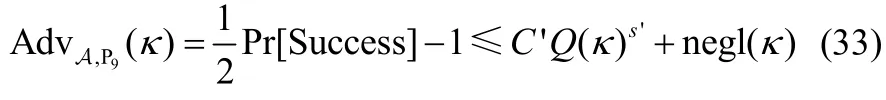
那么，根据实验P1～实验P9的证明过程可知

综上，定理2 成立。

②主动敌手攻击下协议的安全性证明

给定敌手A攻击协议，假设模拟器Sim 为敌手A模拟协议的执行。同样假设服务器A泄露，并对主动攻击下的协议进行安全性证明（假设服务器B泄露的相关证明与此相同）。下文只给出与被动敌手攻击下安全性证明的不同之处。

综上，定理3 成立。

证毕。