跳时短参考载波索引差分混沌移位键控通信方案
杨华,王宇,徐思远,蒋国平
(1.南京邮电大学电子与光学工程学院、微电子学院,江苏 南京 210023;2.南京邮电大学自动化学院、人工智能学院,江苏 南京 210023)
0 引言
混沌现象在自然界中已存在许久,在经济、气象以及工程等许多领域都有应用[1-3]。混沌信号凭借其非周期、宽频谱以及良好的自相关等特性在通信领域中引起了越来越多的关注[4]。基于混沌的通信系统作为一种扩频通信系统,使用宽带非周期性混沌信号作为载波,因此在抗干扰能力、截获概率等方面展示出了优越性[5-7]。其中,差分混沌移位键控(DCSK,differential chaos shift keying)系统凭借其低复杂度和良好的抗多径衰落能力更受欢迎[8-9]。
然而,DCSK 系统采取的传输-参考模式使其有一半的比特能量和时间花费在传输参考信号上,从而导致数据传输速率低、能量效率不理想、误码率(BER,bit error rate)也有待改善。为提高DCSK 系统的能量效率,Kaddoum 等[10]提出了一种短参考DCSK(SR-DCSK,short reference DCSK)系统,该系统将DCSK 发送信号中的参考信号缩短,使其占用的时间少于比特持续时间的一半,有效地提高了数据传输速率和能量效率,同时不会增加系统结构的复杂性。考虑到上述系统的BER 性能并没有得到很大的改善,Xu 等[11]将2 个比例系数分别应用于参考信号和信息信号,通过理论分析和仿真结果发现,对于给定的系统参数,2 个比例系数之间存在的最佳比值使SR-DCSK 系统有更好的BER 性能。考虑到脉冲位置调制(PPM,pulse position modulation)的系统结构简单,Miao 等[12]提出了一种脉冲位置调制DCSK(PPM-DCSK,pulse position modulation DCSK)方案,通过改变信息信号的时隙位置来携带额外的数据比特,具有更出色的BER 性能。
作为5G 无线网络的一项关键技术,索引调制在过去几年中引起了相关研究人员的极大兴趣[13]。通过改变诸如扩频码、载波、天线等传输实体的开关状态,索引调制不仅可以简化系统结构,而且在频谱和能量效率方面具有优势。因此,出现了大量基于索引调制的DCSK 通信方案。Xu 等[14]提出了一种码索引调制DCSK(CIM-DCSK,code index modulation DCSK)方案,该方案通过使用Walsh码索引来传输额外的数据比特,有效地提高了系统的频谱效率和能量效率。Cheng 等[15]提出了2 种类型的载波索引 DCSK(CI-DCSK,carrier index DCSK)方案。这2 个系统使用不同的参数设置和索引选择器来实现载波索引调制以发送额外的数据比特,分别提高了能量效率和频谱效率。Yang等[16]提出了一种高数据速率CI-DCSK(HDR-DCSK,high data rate CI-DCSK)方案。该方案通过利用Walsh 码的正交性将多个承载数据的载波以并行的方式与参考信号一起传输,改善了系统的能量效率和BER 性能表现。Cai 等[17]提出了码索引调制多载波多进制 DCSK(CIM-MCM-DCSK,CIM multi-carrier M-ary DCSK)方案,通过将码索引与多进制的载波差分混沌移位键控系统相结合的方法来提升系统的频谱效率和BER 性能。在PPM-DCSK方案的基础上,Cai 等[18]提出了一种具有索引调制的双模DCSK(DM-DCSK-IM,dual-mode DCSK with index modulation)方案。该方案将PPM-DCSK系统中非激活时隙也用来传输数据比特,因此具有更高的数据传输速率。在载波索引和码索引调制系统的基础上,Cai 等[19]提出了联合载波码索引调制的多进制DCSK(JCCIM-MDCSK,joint carrier-code index modulation M-ary DCSK)方案,在将调制比特送入M 进制DCSK 调制器的基础上,它同时使用载波索引和码索引传输额外的载波索引比特和码索引比特。与单独的索引调制系统相比,JCCIM-MDCSK 具有更好的BER 性能表现。
可是,在上述方案中,参考信号未携带有用信息。为利用参考信号的发射功率,使参考信号携带额外的比特,本文提出一种跳时短参考载波索引DCSK(TH SR-CI-DCSK,time hopping short reference carrier-index DCSK)系统,该系统利用跳时技术改变短参考信号在参考子载波时间段上的位置来携带额外的数据比特,有效地提升了系统的频带利用率、系统能量效率和BER 性能,具有广阔的应用前景。
1 TH SR-CI-DCSK 系统模型
1.1 发射端
为便于理解,表1 列出了本文所提TH SR-CIDCSK 系统的主要参数。

表1 系统主要参数
本文采用切比雪夫二阶映射生成离散混沌序列。在第v个符号周期内,混沌信号发生器生成混沌信号,长度为R,将其送入脉冲成形滤波器生成短参考信号xv(t)为
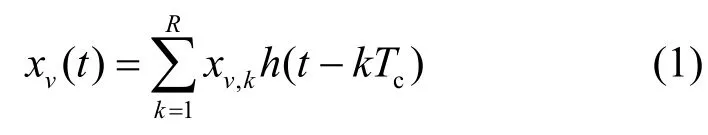
其中,Tc是码片时间,xv,k是混沌信号发生器在第v个符号周期内生成的第k个混沌样本,h(t)是脉冲成形滤波器在时域上的冲击响应。对xv(t)进行S次复制,得到重复混沌信号yv(t),长度为β,作为当前符号周期内的信息载体,即
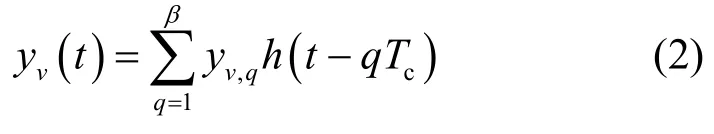
其中,有
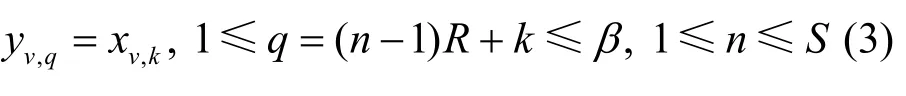
TH SR-CI-DCSK 系统发射端原理如图1 所示。系统可用子载波总数为M+1,其中,利用中心频率为f0的参考子载波发送短参考信号,并将剩余的M个数据子载波从1 到M进行索引标记。系统中传输的数据比特的个数为p+1,包括p个索引比特和一个调制比特。索引比特个数p可表示为

图1 TH SR-CI-DCSK 系统发射端原理
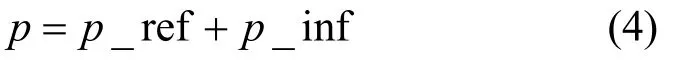
其中,参考索引比特个数p_ref和子载波索引比特个数p_inf 分别为

令Sv_inf=[av,1,…,av,p_inf+1]表示当前符号周期内数据子载波传输的p_inf+1 位数据比特。其中,av,1,…av,p_inf为子载波索引比特,av,p_inf+1为调制比特。首先,通过极性变换将调制比特av,p_inf+1∈{0,1}变成极性调制比特bv,p_inf+1∈{-1,1}。随后,索引选择器将当前符号周期内的子载波索引比特映射为子载波系数dv,m,m=1,…,M。在这M个系数中,只有有效子载波对应的系数等于极性调制比特,所有无效子载波对应的系数均为0。最后,极性调制比特被调制在重复混沌信号yv(t)上并经有效子载波以DCSK 的方式传送出去。本文所涉及的索引选择器的系数使用自然二进编码的方法来映射。以p_inf=2 为例,当子载波索引比特av,1av,2=01且调制比特av,3=1时,生成的子载波系数dv,1dv,2dv,3dv,4=0100,有效子载波即第2 条数据子载波。
令Sv_ref=[hv,1,…hv,p_ref]表示当前符号周期内参考信号传输的p_ref 位参考索引比特。PPM 的调制器根据当前输入的参考索引比特通过自然二进编码的方法确定S个时隙系数。所有系数为0 的时隙内不传输任何信号,系数为1(即有效脉冲位置)的时隙内发送短参考信号xv(t)。以p_ref=2 为例,当参考索引比特hv,1hv,2=10时,生成的时隙系数SPPM=[0,0,1,0],即短参考信号在时隙3 发送。
TH SR-CI-DCSK 发射机在第v个符号周期内的发送信号为

其中,SPPMn表示第n个参考子载波时隙系数,φm和fm分别表示第m个子载波的相位角和中心频率,φ0和f0分别表示参考子载波的相位角和中心频率。图2 给出R=20、p_ref=2、p_inf=2 时混沌信号发生器产生的混沌信号、复制S次后得到的重复混沌信号以及第v个符号周期内的发送信号。
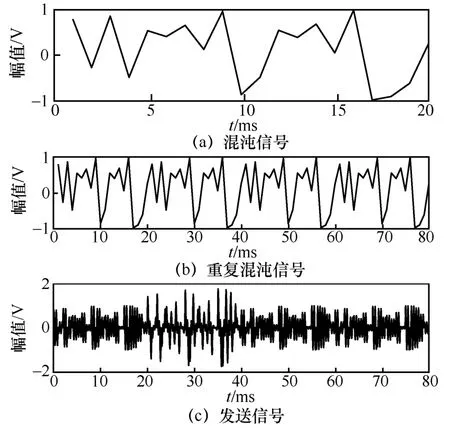
图2 混沌信号、重复混沌信号和发送信号
1.2 接收端
TH SR-CI-DCSK 系统接收端原理如图3 所示。M+1 个正弦子载波和接收到的信号依次相乘,然后输入匹配滤波器进行滤波并在每个qTc时刻采样。采样后的离散短参考信号和离散信息信号分别存储为短参考矩阵AS×R和信息矩阵BM×β。不考虑噪声的影响,矩阵A和矩阵B中的元素可分别表示为
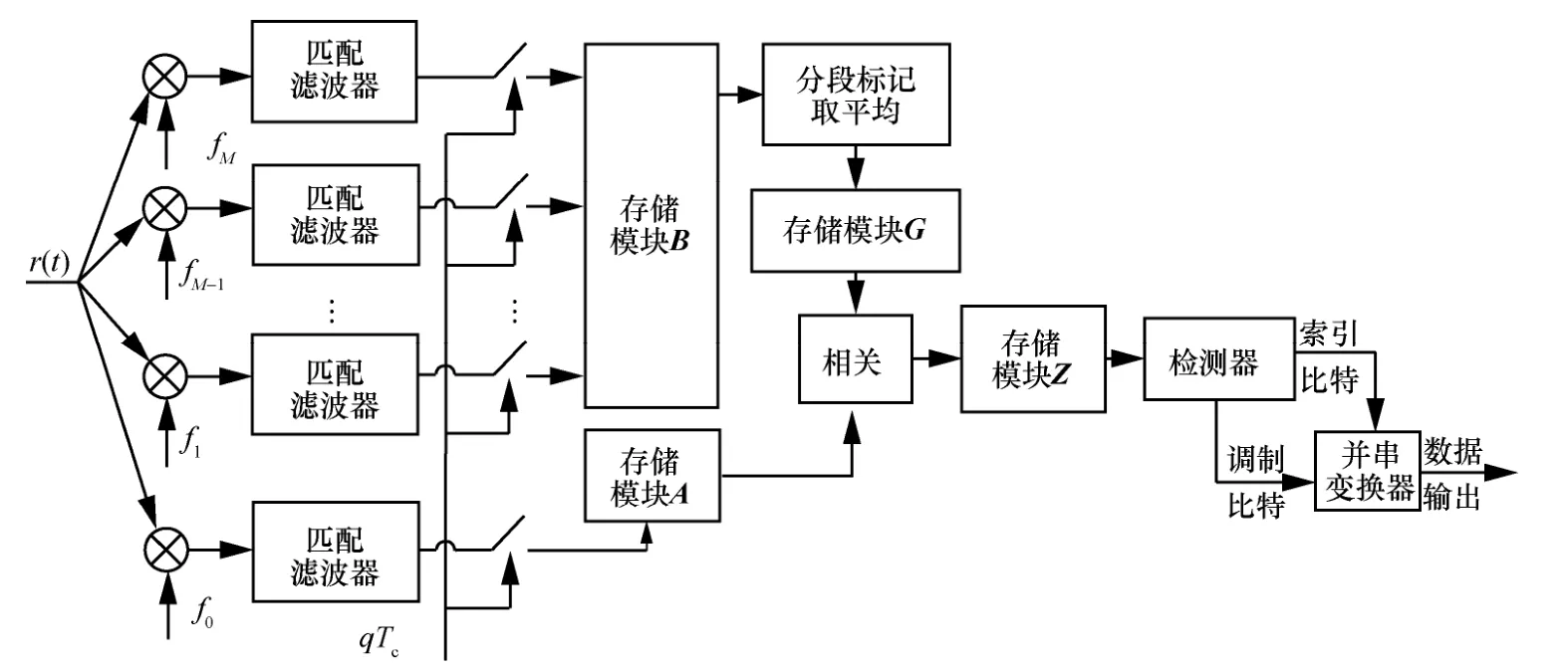
图3 TH SR-CI-DCSK 系统接收端原理

其中,ci_ref和cj_inf分别表示有效参考脉冲时隙的索引和有效数据子载波的索引。
将2 个矩阵分别存储在对应的存储模块A和B中,并将存储模块B中矩阵的每一行分成S段,对每一段相加取平均,得到新的解调矩阵GM×R,矩阵G中的元素可以表示为
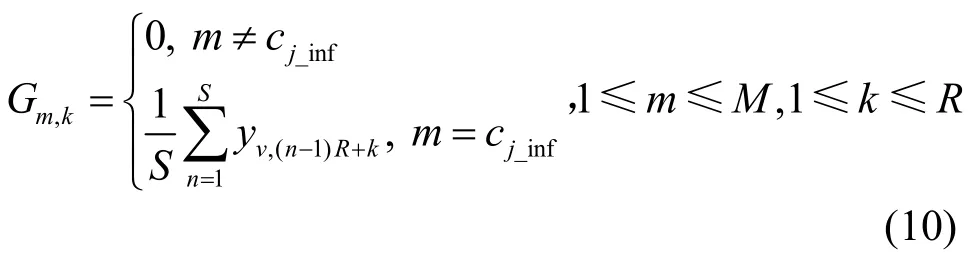
将解调矩阵GM×R存储在存储模块G中,并将其与存储模块A中的短参考矩阵做相关运算得到相关矩阵ZS×M。

将相关矩阵ZS×M存储在存储模块Z中,通过检测器计算其中每个元素的绝对值并取最大值,再根据其行列恢复出参考有效脉冲时隙的索引ci_ref和数据子载波的索引cj_inf。

其中,和分别表示第v个符号周期内参考有效脉冲时隙和有效子载波的索引估计值。
最后,调制比特由Z中绝对值最大的元素的极性符号确定,即

其中,表示恢复出的第v个符号周期内发送的调制比特。
在p_ref=2、p_inf=2、R=20 的情况下,接收端采样开关在4个符号周期内输出的信号波形如图4所示。图4中,接收端在这4 个符号周期内恢复出的有效参考脉冲时隙的索引分别为3、2、1、4;有效的信息子载波的索引分别为1、2、4、3。

图4 采样开关输出信号波形
2 系统BER 性能分析
为了便于分析,假设在第v个符号周期内第一段参考脉冲时隙有效、第一个数据子载波有效。假设全部子载波是完全同步,Zi,j可表示为

其中,表示数据子载波经过平均后的高斯噪声,表示参考子载波的高斯噪声,αv,l表示第l径Rayleigh衰落信道的信道增益,τl表示第l径Rayleigh 衰落信道的信道时延。
当R较大时,可以很容易得到

Zi,j的均值和方差可近似表示为


在解调索引符号时,其正确的条件为有效子载波的相关绝对值大于任意一个无效子载波的相关绝对值。则正确解调当前索引符号的概率可得



其中,efr(·)表示误差函数。将式(19)~式(22)代入式(18)可得

因此,索引比特的符号错误概率可写为

索引比特的BER 为
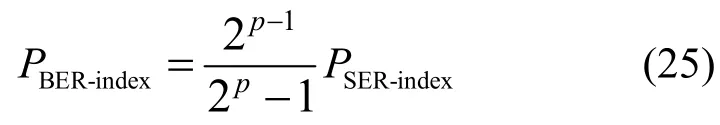
在恢复调制比特时,应该考虑以下2 种情况:1)索引符号恢复错误;2)索引符号恢复正确。
对于第一种情况,调制比特的BER 为

对于第二种情况,调制比特的BER 为

其中,PDCSK是传统的DCSK 系统[21]的BER,计算式为

在每个符号周期内,系统发送p个索引比特和一个调制比特,因此所提系统的BER 值PBER由两部分组成,即索引比特的BER 值PBER-index和调制比特的BER 值PBER-mod。

若只考虑信道系数α1=1、信道时延τ1=0的第一条路径,式(30)还可以用来计算AWGN 信道中系统的BER。
TH SR-CI-DCSK 系统在多径Rayleigh 衰落信道上的整体BER 性能为
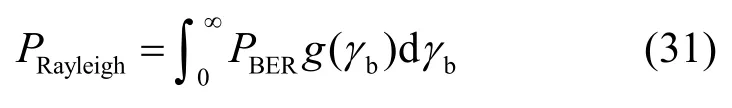
若仅考虑独立同分布L径Rayleigh 衰落信道,γb的概率密度函数为
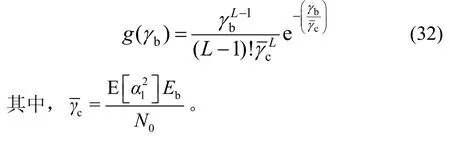
3 效率及系统复杂性分析
3.1 能量效率分析
TH SR-CI-DCSK 系统的符号能量为

其中,每个符号的数据能量由Edata表示,每个符号的参考能量由Eref表示。

一个符号周期内发送的比特数为p+1,则系统的比特能量表示为
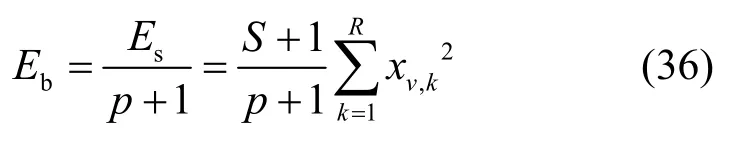
根据数据能量与比特能量比(DBR,data-energyto-bit-energy ratio)的定义,所提系统的DBR 为

在子载波个数相同、信息信号长度相同的情况下,CI-DCSK 系统的DBR 为

与CI-DCSK 系统相比,所提系统在能量效率方面具有明显优势。所提系统发送的数据比特主要由两部分组成:第一部分是通过子载波索引传输的数据比特,第二部分是通过改变发送短参考信号的时隙位置传输的参考索引比特。一方面,所提系统采用短参考能够消耗更少的能量来发送参考信号;另一方面,跳时技术的使用使参考信号上携带额外信息,提高了系统在子载波个数相同情况下的数据传输速率。综上所述,用更少的能量发送更多的数据比特使所提系统具有更高的能量效率。
3.2 频谱效率分析
假设每个子载波的带宽相同并用B表示,TH SR-CI-DCSK 系统和CI-DCSK 系统的频谱效率分别为

TH SR-CI-DCSK 系统与CI-DCSK 系统频谱效率的对比如图5 所示。图5中,数据子载波个数M以及短参考信号长度R不变。从图5 可以观察到,所提系统的频谱效率要比CI-DCSK 系统的频谱效率高,这是因为所提系统随着信息信号长度β变长(即短参考信号复制次数S的增加),参考子载波额外携带的数据比特不断增加,使所提系统的比特速率增大;而在同等情况下CI-DCSK 系统的比特速率并不会发生改变。所提系统和CI-DCSK 系统的子载波个数和信息信号长度相同,所以具有更高比特速率的TH SR-CI-DCSK 系统在频谱方面表现更佳。

图5 频谱效率对比
3.3 系统复杂性分析
为了比较硬件复杂性,表2和表3 分别列出了所提系统和CI-DCSK系统发射端和接收端所需的元件。
如表2和表3 所示,TH SR-CI-DCSK 系统在大部分元件的使用数量上与CI-DCSK 系统基本相同,为了实现参考信号的跳时传输,TH SR-CI-DCSK 发射端增加了一个混沌序列复制器、一个PPM 调制器和一个乘法器;接收端增加了一个平均器和一个存储模块。因此,TH SR-CI-DCSK 系统的硬件复杂性略高于CI-DCSK 系统。

表2 发射端硬件复杂性比较

表3 接收端硬件复杂性比较
在系统计算复杂性分析中,一个符号周期内由发射机和接收机执行的乘法操作总数是一个重要的参数。在THSR-CI-DCSK系统中,发送一个携带p+1个数据比特的信号需要2p_inf+1+2个乘法操作,而解调此信号需要2p_inf+1个乘法操作。因此,所提系统传输p+1个数据比特的计算复杂性为

同理,CI-DCSK 系统传输p+1个数据比特的计算复杂性为

考虑到p=p_ref+p_inf,TH SR-CI-DCSK 系统的计算复杂性明显低于传统的CI-DCSK 系统,且p_ref越大,所提系统在计算复杂性上的优势越明显。
4 仿真结果
本节首先分别在AWGN 信道和三径Rayleigh衰落信道条件下对TH SR-CI-DCSK系统进行仿真,验证第3 节中理论分析的正确性;接着讨论系统参数(如参考信号的长度R和信息信号的长度β)对TH SR-CI-DCSK 系统BER 性能的影响;随后进行不同系统之间的BER 性能比较;最后对系统在非理想条件下的性能表现进行仿真与分析。本节仿真中使用的三径Rayleigh 衰落信道模型参数分别为,τ1=0,τ2=1,τ3=2。
TH SR-CI-DCSK 系统在参考信号长度R=64、信息信号长度β=256的条件下,分别经过AWGN信道和三径Rayleigh 衰落信道时,仿真和理论BER性能对比如图6 所示。从图6中可以看出,式(30)得到的系统BER 理论值与仿真值基本吻合,证明了理论推导的准确性。从图6中还可以看出,当p_inf 增加时,TH SR-CI-DCSK 系统的BER 性能逐渐提升。这是因为β和R固定时,p_ref 不变,此时增加p_inf意味着能够发送更多的比特数据,因此比特能量下降,导致在相同信噪比条件下噪声的影响减小,因此系统可以获得更加出色的BER性能。

图6 TH SR-CI-DCSK 系统的仿真和理论BER 性能对比
AWGN 信道中TH SR-CI-DCSK 系统的BER 性能与R的关系如图7 所示。图7中,信息信号长度β=256,子载波索引比特个数p_inf=5。从图7 可以看出,随着R的增大,系统的BER 性能逐渐变好,达到最佳值后逐渐变差。这是因为当R刚开始变大时,混沌信号自相关方差的迅速变小使系统BER 性能得到提升;随着R继续变大,平均降噪次数S=明显变小,判决变量中噪声变大的趋势占上风,系统BER 性能下降。所以BER 性能先变好后变差。将式(30)对R求一阶导数,即,并令ψ(R)=0,可以求出当前条件下获得最佳BER 性能的短参考信号长度值。

图7 TH SR-CI-DCSK 系统的BER 性能与R 的关系
当短参考信号长度R=64、子载波索引比特个数p_inf=5时,AWGN 信道中TH SR-CI-DCSK系统的BER 性能与信息信号长度β的关系如图8所示。从图8中可以看出,随着β的增大,系统的BER 性能逐渐变好,达到最佳值后逐渐变差。在R和p_inf 一定的情况下,影响系统BER 性能的因素主要有2 个,即系统在接收端进行平均降噪的次数S和系统经过信道时受到的噪声干扰。β刚开始变大时,系统解调端的平均降噪次数S增加,噪声的不利影响变小,系统BER 性能得到提升。但是随着β不断变大,信号在经过信道时受到的噪声干扰越来越多,当降低的噪声影响不足以抵消增加的噪声影响时,便会出现图8中随着β变大BER 性能先变好再变差的情况。将式(30)对β求一阶导数,即,并令Φ(β)=0,可以求出当前条件下获得最佳BER 性能的信息信号长度值。

图8 TH SR-CI-DCSK 系统的BER 性能与β 的关系
AWGN 信道和三径Rayleigh 衰落信道中,TH SR-CI-DCSK 系统、CI-DCSK 系统、SR-DCSK 系统和DCSK 系统的BER 性能对比如图9 所示。图9中,TH SR-CI-DCSK 系统和SR-DCSK 系统短参考信号长度R均设置为64,TH SR-CI-DCSK系统和CI-DCSK 系统子载波索引比特个数p_inf均设置为5,所有系统的信息信号长度β均设置为256。从图9 可以明显看出,在2 种信道中,TH SR-CI-DCSK 系统的 BER 性能都优于CI-DCSK、SR-DCSK 系统和DCSK 系统。
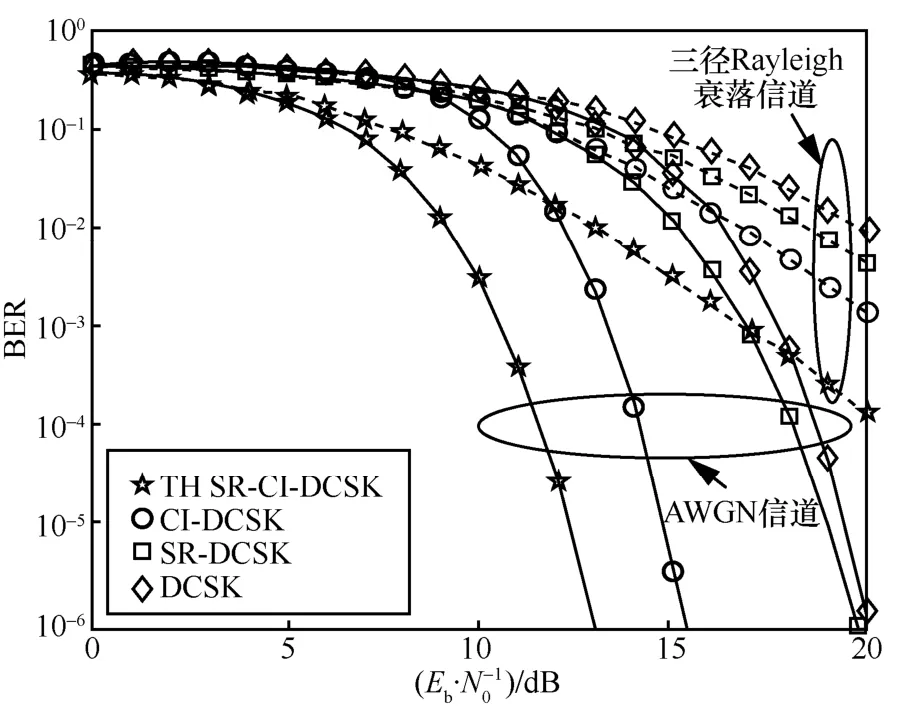
图9 在AWGN和三径Rayleigh 衰落信道上不同系统的BER 性能对比
非理想情况下TH SR-CI-DCSK 系统的BER 性能如图10 所示。从图10 可以看出,当偏移量时,系统的BER 性能将明显下降。这是因为在实际系统中,由于发射机与接收机之间电波在传播过程中受到干扰影响和传输时延而产生差别,接收端中的扩频码与发送端中的扩频码之间码元同步发生偏移,必然会使部分有用信号的功率转换为噪声功率,从而导致系统BER 性能下降。通过对比可以发现,即使是在非理想条件下,所提系统依然具有比其他系统在理想条件下更好的性能表现。因此,所提系统在实际应用中将更具竞争力。

图10 非理想情况下TH SR-CI-DCSK 系统的BER 性能
5 结束语
本文提出的TH SR-CI-DCSK 系统通过使参考信号携带额外数据比特来有效利用参考信号的发射功率,使用高斯近似法推导了所提系统在AWGN信道和多径Rayleigh 衰落信道下的理论误码率计算式,并通过Monte Carlo 仿真将所提系统与传统的CI-DCSK 系统、SR-DCSK 系统和DCSK 系统进行性能比较和分析。结果表明,所提系统具有更高的系统能量效率和频谱效率以及更出色的BER 性能,具有一定的应用前景。

