舰尾流随高扰动模型对直升机着舰悬停控制的影响研究

张 琳，杜智慧，罗 瑜，武 帆

(1.陕西工业职业技术学院 电气工程学院，陕西 咸阳 712000；2.西北工业大学 自动化学院，西安 710129)

0 引言

舰载直升机可以覆盖多种海面任务，为航母编队提供着强有力的支持，它与航母的有效结合能够发挥出最大的执行潜能。而作为战斗链的核心攻击力量，直升机能否在恶劣的海况环境下成功着舰，这关系着整个体系里战斗力的形成。

舰尾流是直升机在着舰最后阶段最主要的干扰来源，它由航空母舰与大气流场的相对运动所产生，直接影响直升机的飞行姿态与位置控制，是导致着舰事故发生的重要因素之一。在着舰降落时，若干扰强度过大，会导致直升机强烈撞击甲板，造成机体结构出现安全隐患，这不仅影响直升机使用寿命，更极大地增加了着舰的危险系数。文献[1]指出，舰尾流扰动涡在航母尾部以85%的行驶速度传播并衰减，越接近甲板着舰点，扰动越大[1]，这将导致直升机在定点悬停阶段变得更难操纵。因此，为保证着舰过程的安全性，研究舰尾气流场的特性、建立相应数学模型、同时给出抑制其干扰的方法是十分必要的。

在舰尾流建模方面，文献[2]通过对航母运动时所产生的舰尾流进行实际测量、风洞试验和水洞试验等各种形式的研究，发现舰尾流是一种非线性、非定常的研究对象，一般可通过频域法、数据库法、CFD法及工程化方法对其进行仿真与计算。其中，工程化方法是通过信号分析技术和频域分析等方法来寻求相对简单、又能反映对象物理特性的建模方法。文献[3]中给出了美军标MIL-F-8785C推荐的较为完善的舰尾流模型，从频谱角度给出了舰尾流各扰动分量的数学描述。

在舰尾流对飞机着舰干扰研究方面，文献[4]仅针对舰尾流的单一分量，即雄鸡尾流对飞机飞行特性的影响展开分析，并未体现大海况场景下舰尾流的复杂特性。文献[5]在舰尾流对舰载机着舰轨迹和动态响应的影响方面做了研究，但所引用的舰尾流模型仅对飞机纵向运动进行了干扰分析，文献[6]进一步分析了舰尾流对纵向甲板着舰点的影响，但两者都未考虑其对直升机在悬停垂向方面的高度保持及位置偏差的影响。文献[7]对引入舰尾流干扰下的飞机姿态输出响应和无干扰的情况作了对比，但在得到干扰数据后，如何对舰尾流的扰动效应进行抑制，则需要进一步提出解决方案。

本文基于上述研究现状，提出在美军标MIL-F-8785C描述的常规舰尾流模型基础上，增加垂向扰动，建立舰尾流随高扰动模型，将其引入直升机着舰悬停控制系统观测干扰输出，并针对传统PID控制下动态控制效果不佳的问题，设计相应的前馈补偿器抑制干扰，通过仿真验证本文建模策略与控制方法的可行性与合理性。

1 舰尾流随高扰动模型的建立

根据美军标MIL-F-8785C对舰尾流的描述，常规情况下，其总扰动主要由以下4部分组成：

1)自由大气紊流(与航母无关)u1、v1、w1；

2)稳态扰动(雄鸡尾流)u2、w2;

3)周期性尾流(航母纵摇诱导产生u3、w3；

4)随机紊流(与航母有关)u4、v4、w4。

将白噪声经过成型滤波器可得到各分量随时间变化的规律，当仅分析直升机纵向运动受干扰的情况时，可得到扰动总量随时间变化的规律：

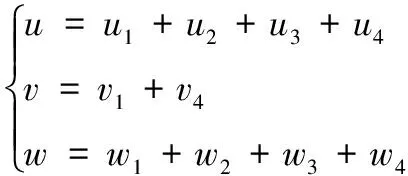
(1)

1.1 自由大气紊流分量

海面自由大气紊流是一种与直升机、航母相对位置无关的低空随机大气紊流分量，呈现出各向异性，美军标MIL-F-8785C给出了它的频谱关系，如下式所示[8]：

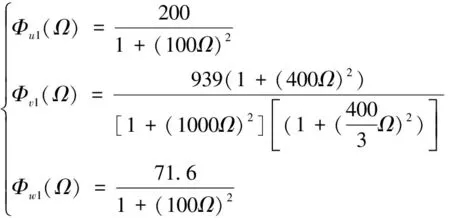
(2)

在对直升机着舰过程中遭遇的自由大气紊流分量进行数值模拟时，需将空间频谱Φ(Ω)转化成时间功率谱S(ω)，根据Taylor冻场假设，可只考虑大气紊流速度的空间分布，假定其不随时间发生变化，则空间频谱与时间频谱满足以下关系：

(3)

式中，ω为时间频率，V*为直升机空速在地面坐标系三轴上的分量，则有：

(4)

式(4) 中的时间功率谱是有理谱，可根据文献[9]中海浪模型的建立方法，将其转换为成型滤波器的传递函数形式：

(5)

式 (5) 即为自由大气紊流分量的传递函数表达式，其中，Vx、Vy、Vz分别为直升机空速矢量V在地面坐标系三轴上的分量。

1.2 稳态分量

图1～2示意了美军标MIL-F-8785C所描述的稳态紊流分量的变化规律，其中：L表示直升机相对于舰船纵摇中心的距离；u2/Vwind、w2/Vwind分别表示扰动的水平分量和垂直分量与甲板风速的比值，它们与L存在一定的函数关系。

图1 前向稳态分量的变化

假定u2以顺风为正，w2以向下为正。前向分量主要集中在直升机距航母纵摇中心约10～480 m的范围内，呈现明显的“公鸡尾”形状，可以看到，在距航母纵摇中心约55 m处时，受到的前向扰动强度最大。若直升机在着舰阶段一直处于顺风状态，则应考虑其受扰后速度变化与悬停高度及定点位置偏差的问题。同时，就垂向分量而言，下洗流从飞机距航母纵摇中心约730 m处开始起作用，上洗流在约160 m处起作用，扰动作用于直升机机体，可使其下沉振荡，产生高度误差，对着舰不利。

1.3 周期分量

舰尾流的周期分量与航母的运动直接相关，主要由航母的周期性纵摇和升沉运动诱导而成，该分量的干扰强度主要取决于航母的纵摇频率与幅值、甲板风速以及直升机到航母纵摇中心的距离这几个因素，美军标MIL-F-8785C归纳出了周期分量的数学模型，如式 (6) 至 (8) 所示[8]：

分析可知，直升机若处于距航母纵摇中心较远的位置，它所受到周期分量的扰动可不予考虑，比如，在距纵摇中心1 000米时，周期分量在水平方向与垂向均为零值，随着直升机逐渐飞近航母，扰动强度开始增大。

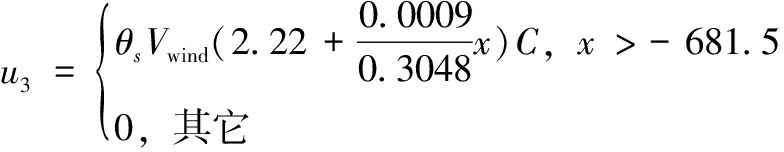
(6)

(7)

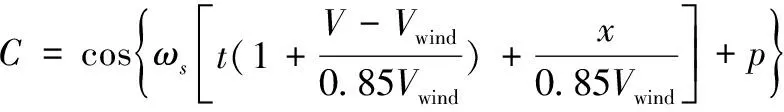
(8)

舰载直升机距航母纵摇中心的距离可表示为：

x=x0+(V-Vwind)·t

(9)

上述式中，ωs为航母的纵摇频率(rad/s)；θs为航母的纵摇幅度(rad);V为直升机实际空速(m/s)；t为直升机飞行时间(s)；p为随机相位(rad)；Vwind为航母运动甲板上空产生的逆向风速(m/s)；x0为直升机距航母纵摇中心的初始水平距离(m)；x为直升机距航母纵摇中心的水平距离(m)。

1.4 随机分量

舰尾流的随机分量u4、v4、w4是由于航母的存在而造成的，幅值相对较小，变化快，呈现出更大的随机性，而直升机本身响应慢，因此随机紊流对直升机着舰过程的影响相对较小。该分量可由白噪声直接经过一个成型滤波器来得到，具体仿真结构如图3所示。

图2 垂向稳态分量的变化

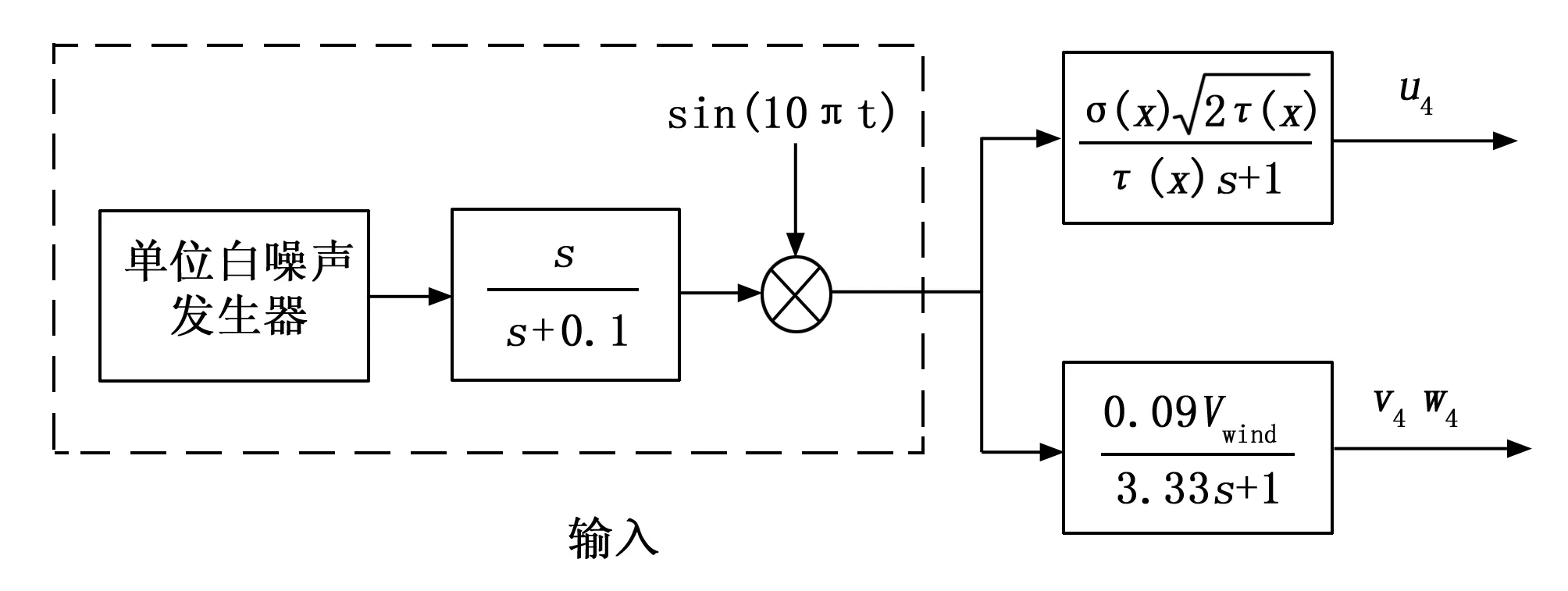
图3 随机分量仿真结构图

其中：σ(x)是随机尾流分量的均方根，τ(x)为时间常数。

1.5 随高扰动模型

为研究直升机在着舰悬停阶段受舰尾流的干扰情况，不仅要研究纵向运动的规律，还应将垂向高度变化的因素考虑进来。由文献[10]可知，当前国内外通常采用曲线拟合的方法来对垂向气流扰动场的物理特征及高度变化进行数值模拟和趋势分析，文献[11]指出，可通过建立简单的数学函数模型，通过其数学变化规律来表现扰动场信号的强弱程度。

根据上述文献中对垂直波长的数据拟合趋势，结合指数函数的变化规律，同时参照文献[12]给出的着舰环境等级描述，以6级大海况作为背景，在MATLAB中拟合出垂向扰动强度的曲线模型，如图4所示。

图4 拟合舰尾流垂向扰动强度趋势

其拟合表达式如下：

(10)

式中，h为舰尾流场距离甲板平面的高度；I(h)表示随高度变化的气流扰动强度，变化范围在0～1内。

基于MIL-F-8785C军用标准描述的舰尾流模型，结合上述高度变化扰动数学模型，对舰尾流进行综合建模，结构如图5所示。

图5 舰尾流综合仿真结构图

设置综合仿真条件：白噪声功率为1，采样时间0.02 s，航母纵摇运动的频率0.6 rad/s、幅值5/57.3 rad、甲板上空风速16 m/s，假定直升机以30 m/s的速度从距航母纵摇中心1 000 m的远处飞向航母，结合本节舰尾流随高模型，对其扰动进行综合仿真，结果如图6～8所示。

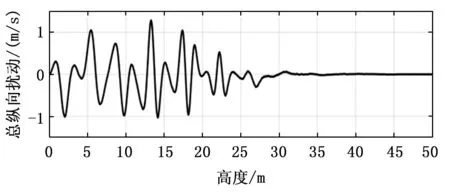
图6 舰尾流纵向扰动分量

图7 舰尾流侧向扰动分量

图8 舰尾流垂向扰动分量

结合上组仿真结果图可知，直升机在距甲板上空较高处飞行时，舰尾流扰动作用不明显，此时可不予考虑；随着飞行高度的不断下降，扰动强度按拟合规律逐渐增大，直升机在距航母3 ～15米的高处飞行时，受到的扰动相对明显，同时可知，在此高度范围内，垂直分量的振荡幅度最大。仿真结果更贴合实际地模拟出了舰尾流对直升机飞行在不同高度时的扰动影响。

舰尾流是设计直升机着舰悬停控制系统时的重要考虑因素之一，在结合其各分量数学模型及垂向气流场变化规律的基础上，建立好舰尾流随高扰动数学模型后，便可进一步对舰尾流扰动场作用在直升机着舰过程中的影响进行研究与分析。

2 舰尾流扰动对着舰悬停的影响

2.1 直升机着舰悬停控制系统结构

在着舰最后阶段，直升机盘旋于甲板上空进入定点悬停模态，该模态是在具备姿态控制、高度控制的基础上，以位置反馈信息为基准的精确位置控制。图9为着舰悬停控制系统的结构框架，利用传统的高度、姿态、位置三个环节的PID控制器，将期望悬停点信息与直升机当前位置姿态信息同时传进控制解算模块单元，计算得到期望直升机实际位置与悬停点的位置偏差，以此为控制变量，进而调整直升机的高度、姿态与位置，以到达悬停的目的。

图9 定点悬停控制结构图

图9中，直升机的系统建模会受到质量时变、高空重力加速度变化、弹性形变气动外形、飞行状态参数等众多因素的影响，若将所有因素纳入考虑范围，系统的数学模型势必极其复杂，因此，直升机数学模型的建立基于以下几点假设：

1)视直升机为刚体，其质量为常数，忽略弹性形变和旋翼姿态变化的影响；

2)假设地面坐标系为惯性坐标系，重力加速度视为定值；

3)忽略地球的曲率，即所谓的“平板地球假设”；

4)假定重力加速度不随飞行高度变化；

5)直升机具有对称平面，惯性积Ixy=Iyz=0；

6)忽略纵向、横侧向运动间耦合[13]。

据此，直升机小扰动线性化方程的状态空间形式如式(11)：

(11)

式中,①状态变量:

(12)

②输入变量:

(13)

依次代表纵向周期变矩、横向周期变矩、尾桨桨距、总距。

通常，直升机上各主要气动参数与扰动量成线性变化关系，以此来研究直升机性能，既使问题简化，又能达到应有的准确度。

式(11)中：C=I9×9，D=09×4

(14)

(15)

2.2 引入舰尾流干扰后的系统响应

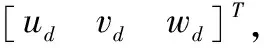
因此，引入舰尾流随高模型后的直升机的状态方程需改写为：

(16)

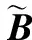
(17)

综上，在直升机悬停飞控系统中引入6级海况下的舰尾流随高扰动模型进行仿真，观测其输出响应，条件设置：假定直升机起始位置对舰坐标为(0,0)，定点悬停位置坐标(60,60)，初始飞行纵向地速2 m/s，侧向地速0 m/s。在图4所描述的拟合规律中，当直升机悬停在距离舰船高5～10米时受到扰动强度较大，可设定直升机理想悬停高度为6米，仿真结果如图10～17组所示。

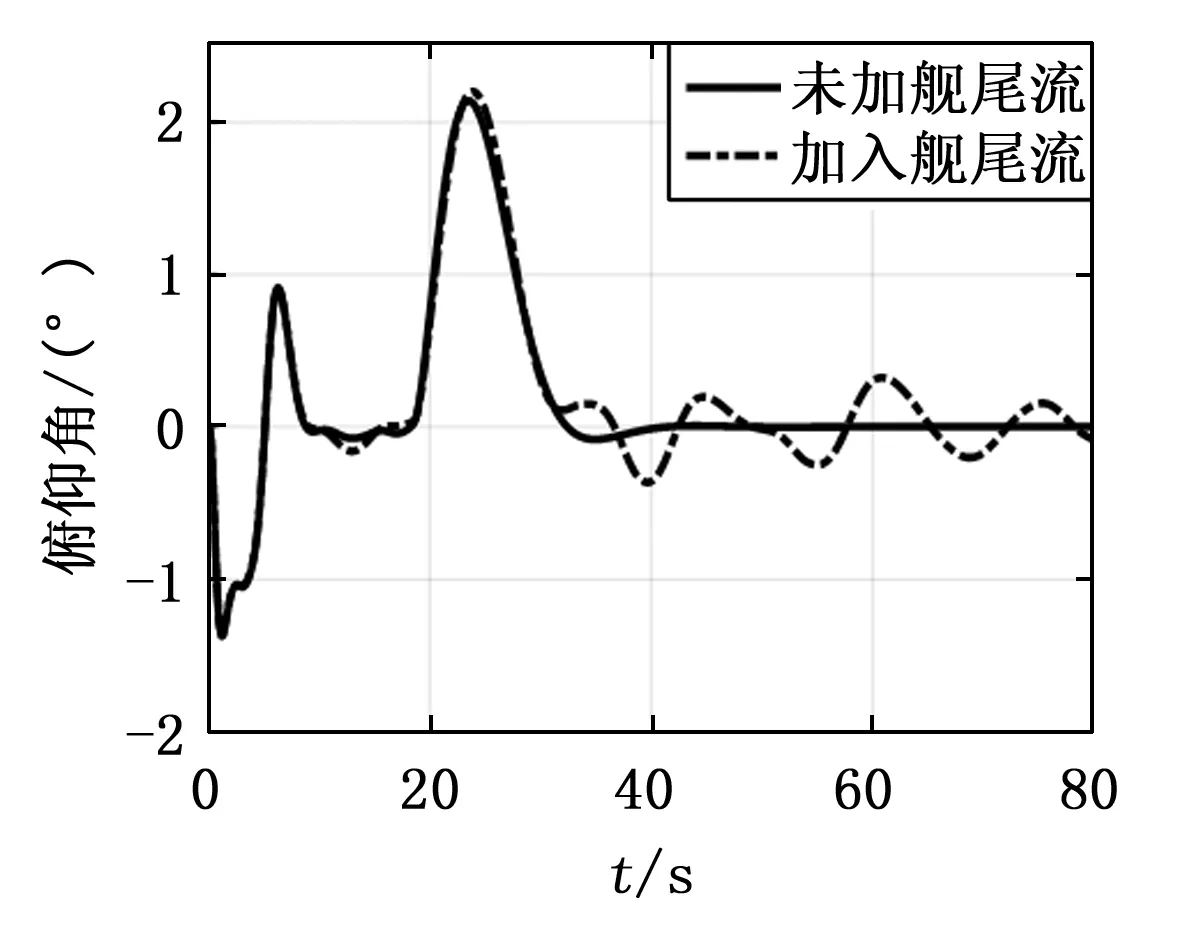
图10 俯仰角响应

图11 倾斜角响应

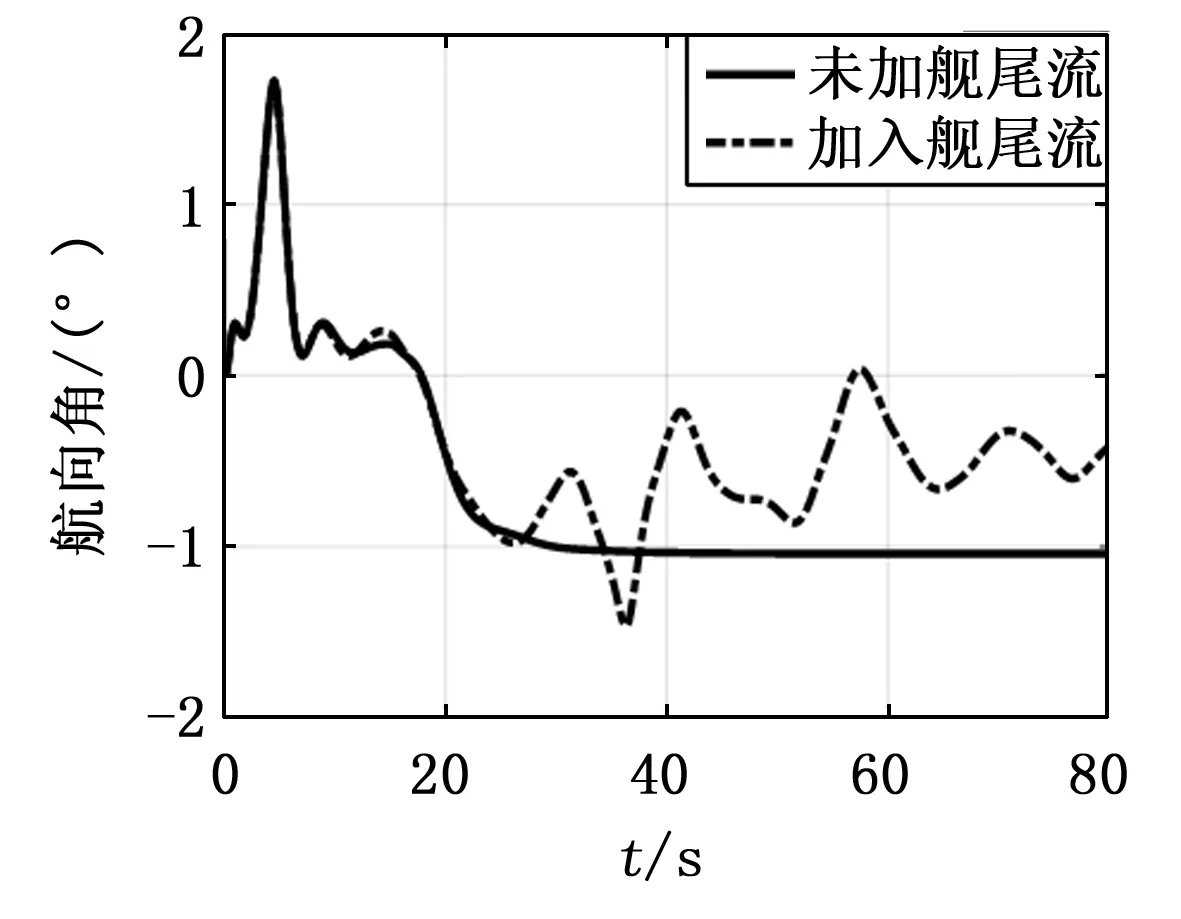
图12 航向角响应

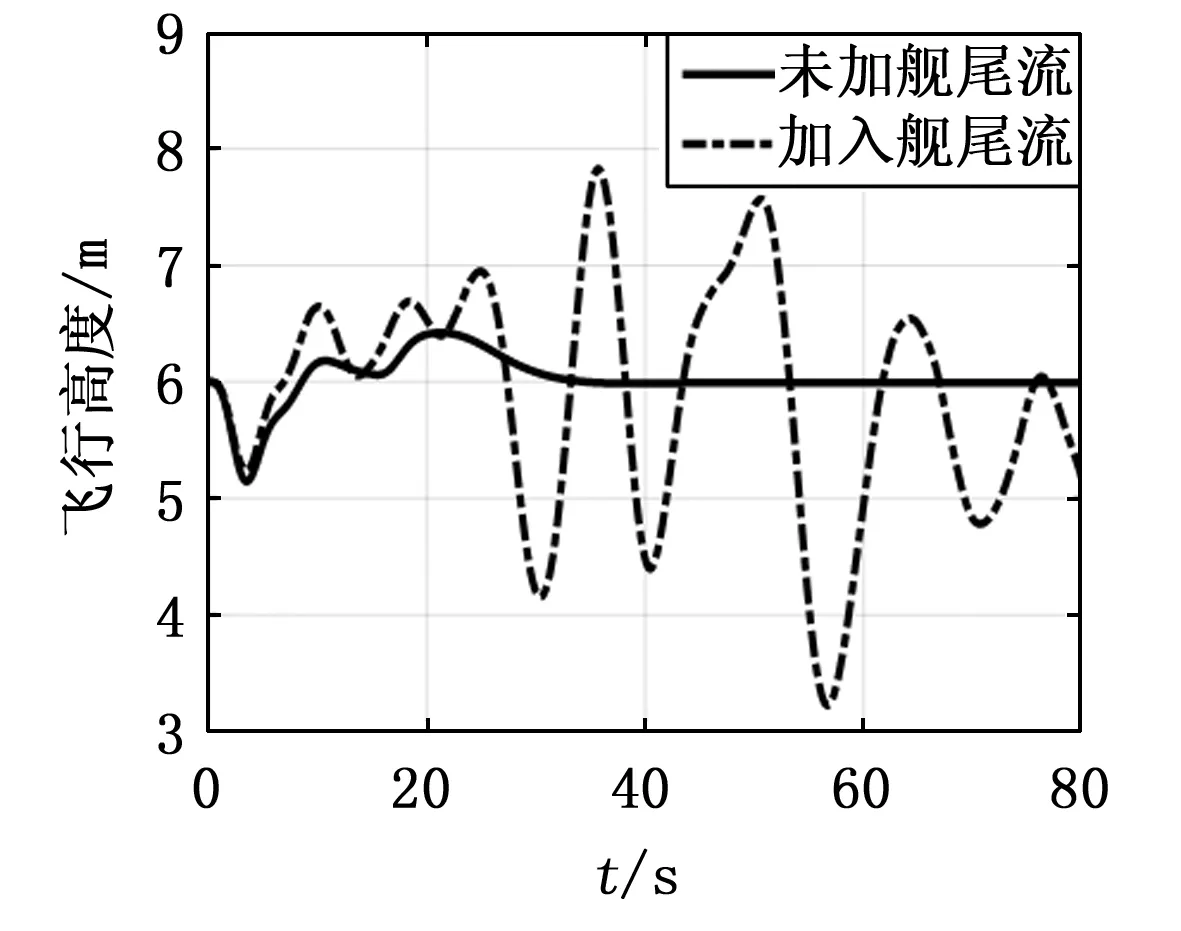
图13 高度响应

图14 纵向地速响应

图15 侧向地速响应

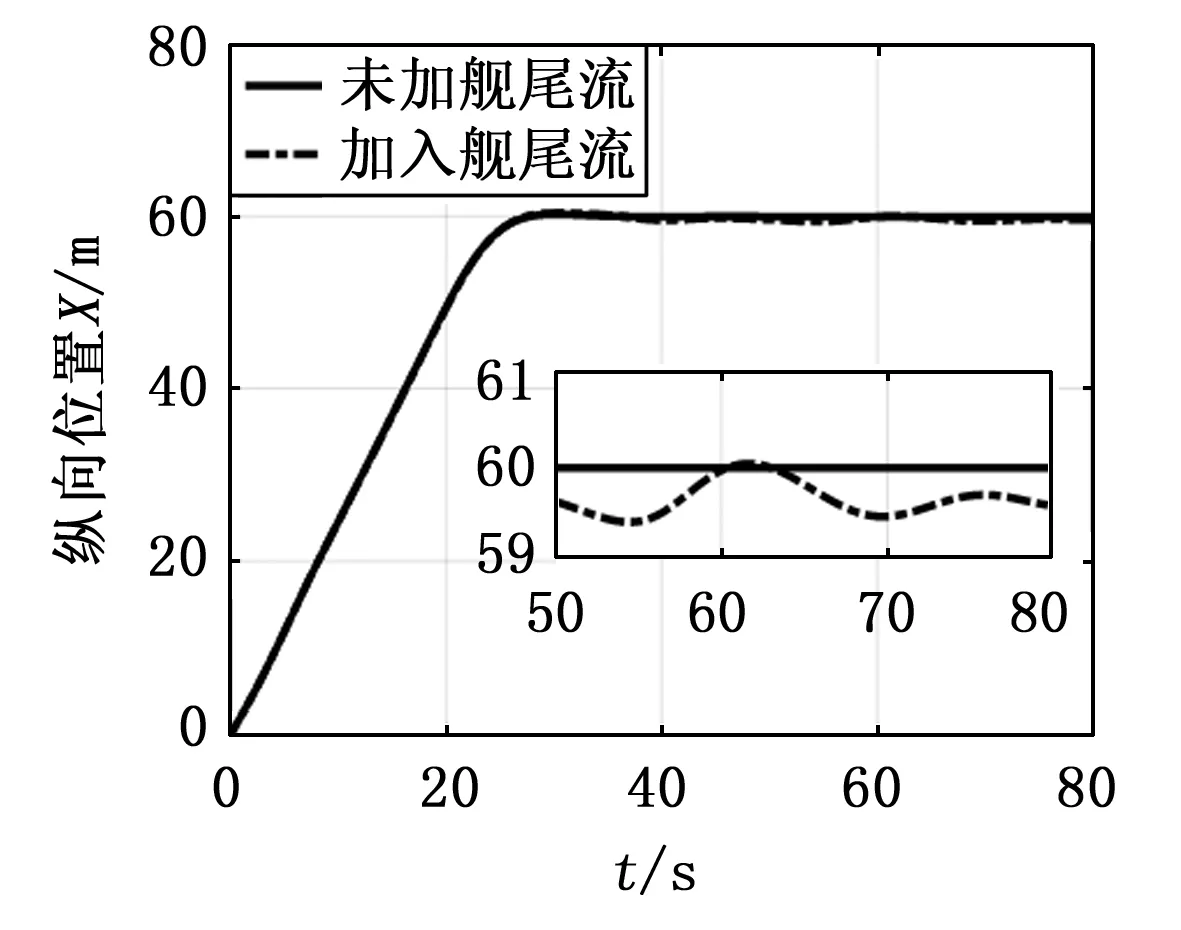
图16 纵向位置响应

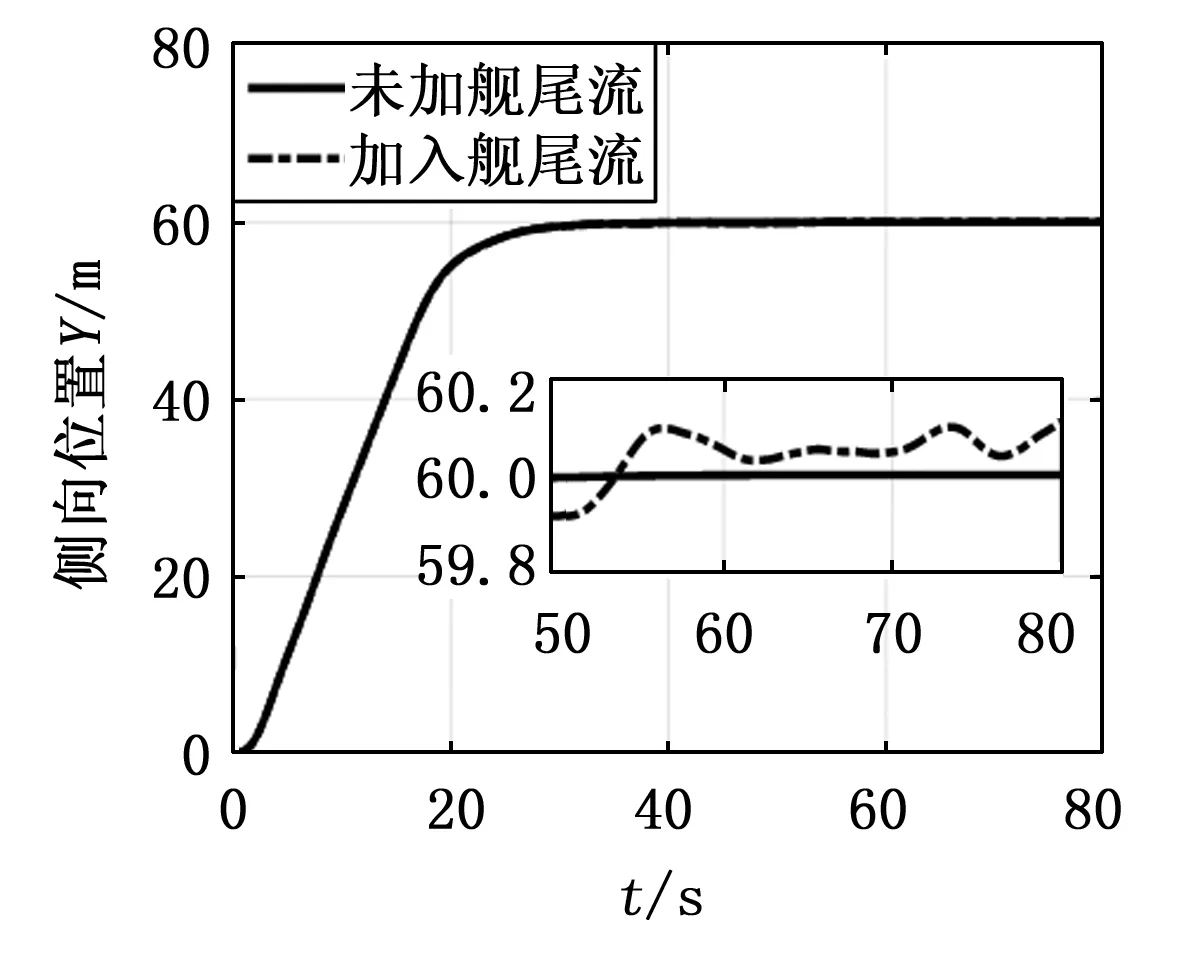
图17 侧向位置响应

结合文献[14]中给出的直升机悬停系统的动态性能指标要求与仿真结果，对比如表1所示。

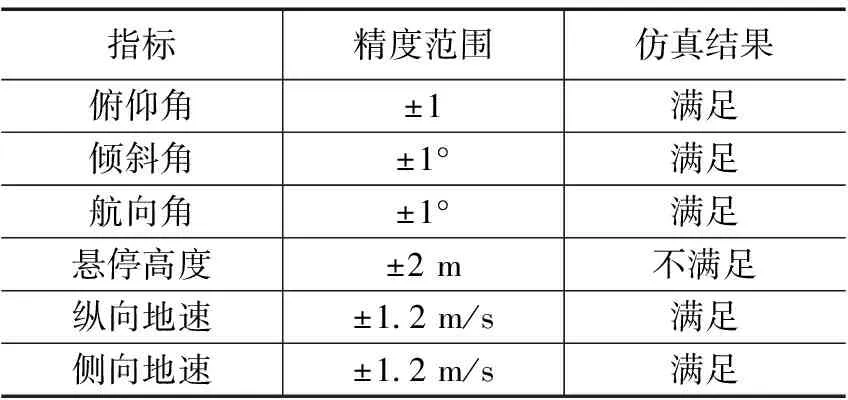
表1 着舰系统输出响应性能情况

分析仿真输出响应可知，引入舰尾流扰动后，直升机悬停时的俯仰角、倾斜角、航向角出现最大1度的姿态误差，满足精度要求，这表明传统的PID控制对飞行姿态的调节控制效果良好。同时，侧向位置的波动误差小于纵向位置，体现了文献[15]中描述的直升机悬停时对侧向气流不敏感的特点。但是，由图13可知，飞行高度的输出偏差较大，在悬停过程中出现最大约2.7米的误差，导致机体始终无法稳定在期望悬停点。若此时着舰，直升机在悬停点处大幅度振荡，难以保持稳定平衡状态，严重时不但无法成功着舰，还会造成严重的机体损毁与飞行事故。因此，采取合理的方案和措施抑制舰尾流扰动，将其负面扰动效应降至最低来确保直升机能够安全平稳地降落到着舰点，则显得十分必要。

3 前馈补偿抑制舰尾流扰动

舰尾流扰动，特别是其垂向气流分量对直升机悬停操纵性能影响较大，主要表现在传统PID对直升机在悬停高度的保持上控制效果不佳，据此，本文设计前馈补偿器来减小扰动负面效应。

图18给出了按干扰补偿的前馈控制原理结构图，其中G(s)、Gn(s)、Dn(s)分别对应系统的前向通道、扰动通道和前馈通道的传递函数。

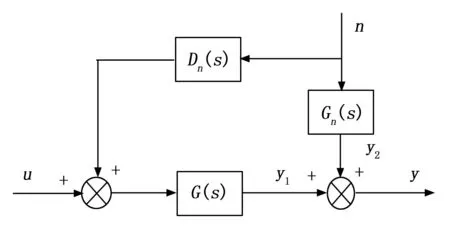
图18 前馈控制原理图

假定输入u=0，以n作为扰动输入，y为输出，由此可得：

Y(s)=Y1(s)+Y2(s)=[Dn(s)G(s)+Gn(s)]·N(s)

(18)

根据不变性原理：y≡0，则有：

(19)

整理可得前馈控制器的传递函数为：

(20)

据此，分别对直升机的俯仰、倾斜高度通道分别设计前馈补偿器。这里仅以高度通道为例，针对舰尾流的垂向扰动分量来设计前馈补偿器。将舰尾流分量作为直升机的输入引入整个系统后，首先推导出以给定垂向速度wg为输入，垂向速度w为输出的开环传递函数，再推导出以舰尾流垂向分量wj为输入，垂向速度w为输出的开环传递函数，最后可计算得到针对舰尾流垂向分量扰动的前馈控制器的传递函数：

DH(s)=

(21)

为方便工程上的实现，又能保证在工作频段内的频率特性尽量接近，对DH(s)做适当的处理，取如下形式：

DH_adjust(s)=

(22)

以高度通道为例，将对应前馈补偿器引入控制系统，其简化结构如图19所示。

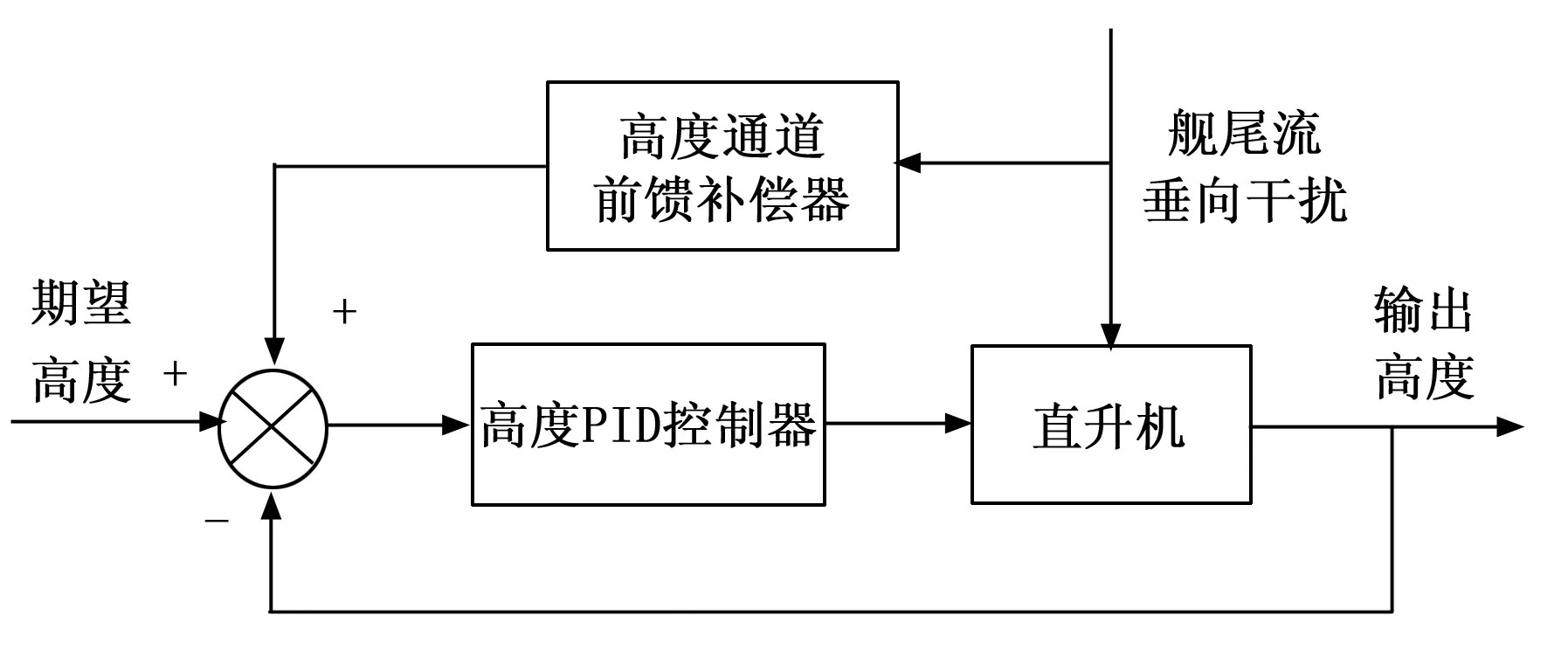
图19 引入高度通道前馈补偿结构图

保持第2.2节的仿真条件不变进行仿真，结果如下图组所示。

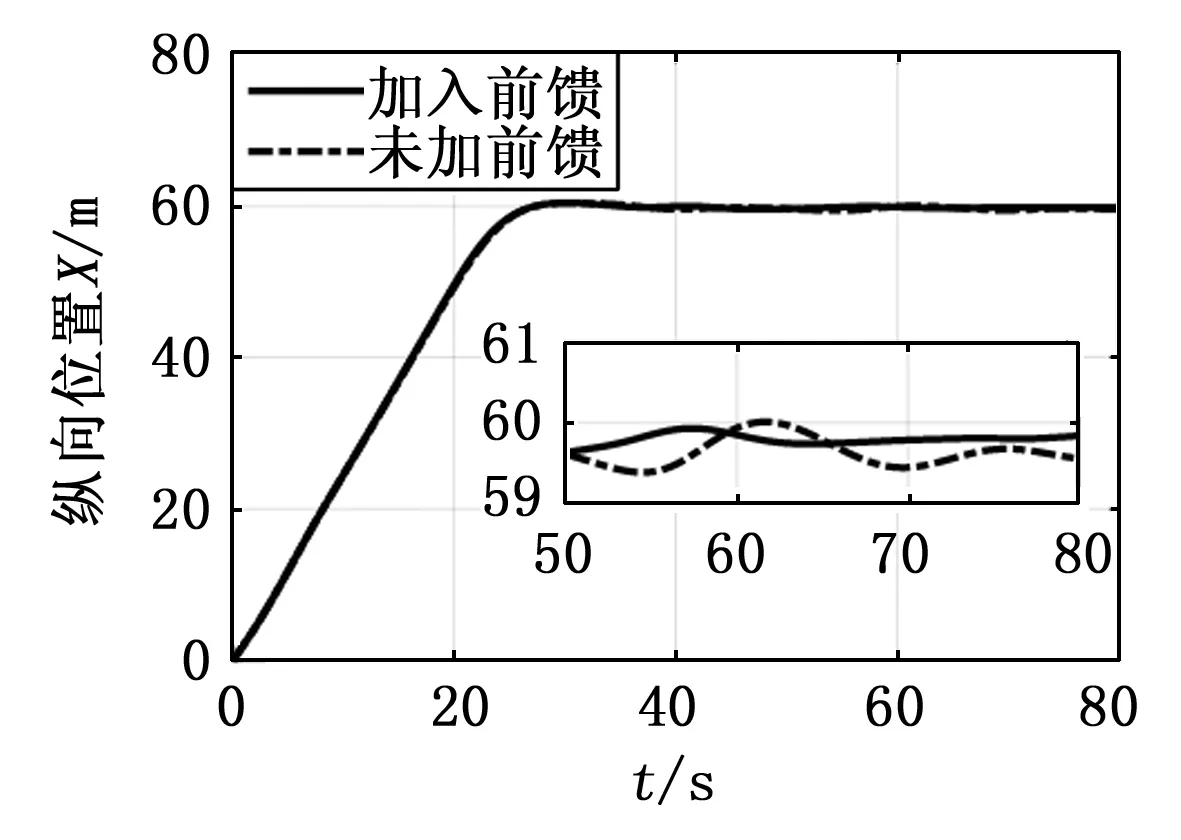
图20 纵向位置振荡对比

图21 侧向位置振荡对比

图22 飞行高度振荡对比

由于传统PID控制下的姿态角保持良好，满足悬停性能指标要求，因此，在做补偿前后输出响应的对比时，如上组图，本文只选取飞行高度及横纵向位置输出响应作以分析。同时，如图23所示，为更直观表现前馈补偿前后飞行高度的控制效果，在MATLAB中采集随飞行时间持续变化的误差数据并绘制响应曲线。

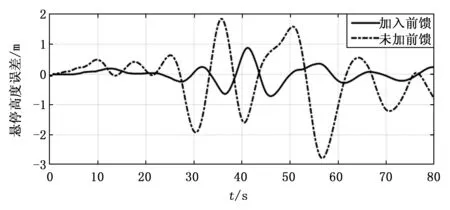
图23 悬停高度误差对比

从仿真结果可以看到，系统加入前馈补偿器后，舰尾流带来的扰动明显被削弱，纵向位置与横向位置的波动幅度变小并渐趋稳定。同时，飞行高度的振荡抑制效果最为显著，其误差从受扰后的最大约2.7 m减小至0.7 m，直升机最终稳定在悬停点 (59.85,59.74)处，悬停保持高度6.15米，满足悬停着舰时的精度要求。由此可见，前馈补偿器的增加，可以在传统PID控制的基础上提高控制精度，且有效抑制外界干扰，最终使误差收敛到实际允许的可控范围内，保证了系统的动态稳定性。

4 结束语

本文在美军标MIL-F-8785C 描述的舰尾流模型的基础上，提出并建立了一种舰尾流随高扰动数学模型，将其引入直升机着舰悬停系统。针对传统PID控制对直升机受扰时悬停高度保持不佳的问题，设计了前馈补偿器改善控制性能。通过仿真，与已有策略进行了对比分析，结果表明，直升机受扰系统在增加前馈控制后，其高度及纵横向位置输出响应振荡幅度明显减小，精确性与鲁棒性均有所提升。本文的研究为直升机着舰时的受扰控制问题提供了一定的数学扰动模型基础与控制策略方案，且可扩展适用于不同等级海况下的应用场景，具备一定的工程参考价值。