基于NPP/VIIRS夜间灯光图像的GDP智能预测模型研究

王森， 蔡小莉， 鲍云飞， 詹邦成

(1.武汉大学信息管理学院， 武汉 430072； 2.河南大学河南省大数据分析与处理重点实验室， 开封 475004； 3.北京空间机电研究所， 北京 100094)

近十年来，由于数据共享政策和传感器的快速发展，夜光遥感成为了遥感领域的热门分支之一。夜光遥感已经被广泛应用于人文地理、区域经济、地缘政治等研究领域，甚至金融行业也开始利用夜光遥感数据。由于数据丰富和成本低廉，卫星遥感是夜光遥感的主流手段。遥感方法是从空间角度对社会经济发展状况进行测绘和分析的最有效和最广泛使用的手段之一。遥感影像以其覆盖面广、效率高、客观性强等优点，为人类提供了海量的空间信息，在建成区提取、土地扩展探测、土地利用制图、土地覆盖变化分析、城市景观结构检测、城市空间结构分析方面有丰富的应用。在这些研究方向中，利用直接探测到的长时间序列夜间灯光进行国内生产总值(gross domestic product，GDP)的估算是最具代表性的衡量人类社会活动的发展方向。

夜间灯光(nighttime light，NTL)遥感影像通过传感器记录地球表面的夜间光，可以探测来自城市、城镇和工业区的灯光，在人类社会经济活动检测方面显示出良好的性能。GDP可以有效地反映一个国家的国力和财力[1]，准确的像素级GDP数据是了解区域经济动态的基础，是定量分析不同行政区划、不同自然属性和人文属性地区经济差异的基础。不同地区的发展模式呈现出更加突出的地区差异。当今世界上大多数国家或地区根据当地需求独立制定GDP统计口径，导致无法直接比较国家/地区之间的统计数据，这会影响使用效率，很难有效客观准确地反映GDP的时空演化规律和精细化的区域发展研究[2]。当使用经济统计方法测算GDP时，会存在以下局限性：①统计尺度不一致、统计单位内部数据不统一等问题，难以在精细尺度上反映区域经济发展的差异；②在一些偏远地区，其经济资料难以获取，且数据的可靠性不高；③对于少数地方、少数企业、少数单位在GDP统计时存在弄虚作假和统计造假行为、统计违法违规的现象，也成“挤水分”等现象。传统的方法在预测GDP时，提取模型的建立方法时大多为简单的线性回归模型、幂函数回归模型、二次函数模型、多项式法等模型，模型在构建时太传统，因此难以给出准确地预测。准确地计量GDP，对于了解区域经济的动态变化，满足跨学科研究的需要具有重要意义。

夜间灯光数据可以弥补上述所说的不足，与传统的社会经济普查相比，遥感影像在描述GDP预测方面具有明显的优势。首先，夜间灯光数据不受区域间价格因素的困扰。目前，中国仅在地级城市之间计算各种价格指数，如果把每个县的GDP数据进行之间比较，就无法消除在地区之间产生的价格因素。其次，夜间灯光数据包括的市场经济的商品和服务不仅是以GDP衡量的，而且还包括市场不提供的商品和服务的价值，因此它对于反映一个国家或地区的经济发展是很真实的。夜间灯光数据作为一种全球无差别的夜间观测量，以其独特的方式描述地球经济活动强度。它可以覆盖整个世界，并且不由于行政区域的差异而产生差异，因此，夜间灯光数据可以用作独特的时空输入，在预测GDP方面得到了广泛的应用[3]。Nataliya等[4]利用DMSP/OLS(defense meteorological satellite program/operational linescan system)数据研究证实了利用夜间光卫星测量数据重建经济活动地理格局的可行性，且夜间光强度往往随着人口密度和人均GDP的增加而增加。范强等[5]通过构建多项式预测模型，分析了比较长时间序列灯光集和GDP之间的关系。Zhou等[6]定量研究了NTL与GDP和人口之间的相关性，研究结果表明夜间灯光与GDP和人口具有显著的正相关。并通过一系列不平等系数，得出中国中西部存在明显的区域差异。研究使用的夜光遥感数据是栅格数据，每个图像中蕴藏着大量的数据信息。从夜间灯光数据中可以看到光亮度的变化和分布，从而提供更多的时间和空间信息。

目前利用Suomi国家极轨伙伴关系(national polar-orbiting partnership，NPP)卫星携带的可见红外成像辐射计套件(visible infrared imaging radiometer，VIIRS)的数据进行估算经济参量的研究相对较多，但很少有研究使用VIIRS数据利用机器学习算法进行GDP预测。为此，利用长时序夜间数据建立长三角地区GDP智能预测模型，以此对该地区的GDP进行及时有效地预测，并进一步分析不同地区的经济差异。研究结果为夜光数据的应用领域和应用方式，以及地区的可持续规划和发展提供了决策依据。

1 基础理论

随机森林(random forest，RF)模型是一种Bagging集成算法，具有灵活度高、不易过拟合、准确率高的特性，有广阔的应用场景[7]。随机森林的有关理论可参考李倩倩等[8]的研究。随机森林可以用来解决回归问题和分类问题，当它被用来做回归问题时，原理是通过对样本进行随机抽取并放回，生成对个决策树，并把决策树的结果进行平均作为模型输出[9]。因此，随机森林能够对高维特征数据进行评估及处理的能力[10]。

随机森林有两个重要的参数：树的数目和分割的特征数。与多元线性回归、地理扩展回归和人工神经网络方法相比，随机森林算法不需要考虑多重共线性问题，可避免过度拟合问题，运算速度高且适合处理高维特征数据等优点[11-13]，因此在人口模拟，生态学，经济学，医学等领域均运用较广泛。对于随机森林来说其算法的核心步骤如下。

步骤1使用Bootstrap方法选择可替代的样本，依次选择m个集合作为样本。共生成ntree棵树的训练集。

步骤2对ntree棵树进行训练并产生相应的模型。

步骤3根据分区索引为每个拆分选择最佳特征。

步骤4每个决策树都是独立拆分的，并且在决策树的拆分过程中不需要修剪，直到该例程的所有训练示例都属于同一类别为止。生成的多个决策树形成一个随机森林，并且将每个决策树的分类或预测结果进行整合。

算法流程图如图1所示。

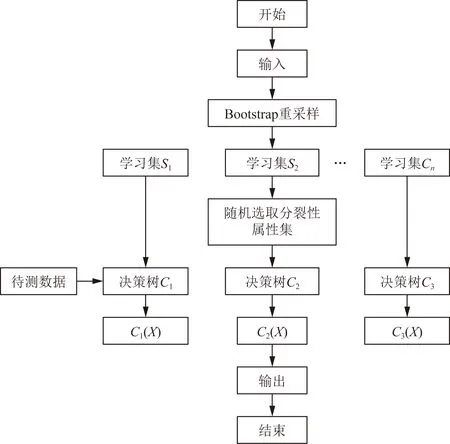
C1为学习集S1产生的模型;C2为学习集S2产生的模型;C3为学习集S3产生的模型;X为模型的最佳特征图1 随机森林算法流程图Fig.1 Algorithm flowchart of random forest

2 研究区域及数据集处理

2.1 研究区域

中国的长江三角洲(117°29′E～123°01′E，27°64′N～34°33N)地区是指上海，浙江，江苏和安徽省(三省一市)。地势主要包括安徽苏滨河平原、长江三角洲平原和里下河平原。根据2019年长三角区域一体化发展规划，长三角城市群包括214个县。它的面积为22.5×104km2，总人口约为2.43亿，研究区域如图2所示。

图2 研究区域Fig.2 Study area

2.2 NPP/VIIRS夜间灯光数据预处理

VIIRS原始数据采用WGS1984坐标系，其夜光影像获取时间为凌晨1:30，VIIRS空间分辨率为15″[14]，这会造成影像随着纬度的增大而减小的问题。为了避免影像由于坐标系发生的变形影响及便于方便计算影像面积，将所有的NPP/VIIRS影像数据都转换为Albers等积投影坐标系。最后将影像重采样为0.5 km×0.5 km大小的网格。研究中使用的第一版VIIRS月合成数据并没有处理如极光、火光和其他短暂性光源的影响，因此存在背景噪声，灯光辐射率值存在负值、极小值、极高值的特点，这些噪声和异常值数据的存在会影响数据模拟精度。针对这种情况，根据Shi等[15]的方法做了以下处理：把小于零的值设为0.001(近似为0，对统计分析没影响)，把背景值设为0；将大于235的数值设为235，以删除一些异常值。由于原始获取的 NPP/VIIRS 夜间灯光数据产品时间尺度为月度产品，进行空间化时需要使用合成后的全年数据，采用平均值法对其进行合成获取得到2012—2018年长三角区域NPP/VIIRS年度数据。研究区VIIRS影像如图3所示。

2.3 其他辅助数据

除NPP/VIIRS夜间灯光数据之外，研究区还采用建成区面积、户籍人口、全社会用电量等其他辅助数据。其中经济统计数据从《中国城市统计年鉴》中查找并收集了长三角地区214个县的2012—2018年GDP数据(单位：亿元)。表1列出了所使用的数据。

DN(digital number)表示像元，DN值越大，亮度越亮图3 处理后的研究区夜光数据Fig.3 Processed nighttime data of the study area

表1 其他辅助数据Table 1 Other auxiliary data

3 贝叶斯优化改进的随机森林模型

3.1 贝叶斯优化技术框架结构

贝叶斯优化算法是所有优化算法中较高效的一种优化算法，许多研究表明贝叶斯优化可以替代解决复杂问题中的其他优化算法。它使用先前搜索到的点的信息来确定下一个搜索点。其原理是在不知道目标函数时，充分利用已存在的采样点来预测函数的最大值[16]。

在数学上，可以统一替换问题描述为替代目标功能的替代最优解，可表示为[17]

(1)

式(1)中：x为要进行优化的参数；X∈R；x*为要进行优化的参数集合；f(x)为要预测最大值的目标函数。

算法的思路是首先生成一个初始候选解集合，然后根据这些点寻找下一个有可能是极值的点，将该点加入集合中，重复这一步骤，直至迭代终止。最后从这些点中找出极值点作为问题的解。

这里的关键问题是如何根据已经搜索的点确定下一个搜索点。贝叶斯优化根据已经搜索的点的函数值估计真实目标函数值的均值和方差(即波动范围)，如图4所示。由图4(a)可以看出，两条虚线所夹区域为在每一点处函数值的变动范围，在以均值即红色曲线为中心，与标准差成正比的区间内波动。在搜索点处，红色曲线经过搜索点，且方差最小，在远离搜索点处方差更大，这也符合的直观认识，远离采样点处的函数值估计的更不可靠。根据均值和方差可以构造出采集函数，即对每一点是函数极值点的可能性的估计，反映了每一个点值得搜索的程度，该函数的极值点是下一个搜索点，如图4(b)所示。

算法的核心由两部分构成：对目标函数进行建模即计算每一点处的函数值的均值和方差，通常用高斯过程回归实现；构造采集函数0，用于决定本次迭代时的采样位置。

红色曲线为估计出的目标函数值即在每一点出处的目标函数值的均值；两条虚线所夹区域为在每一点处函数值的变动范围图4 贝叶斯优化的原理Fig.4 Bayesian optimization principle

3.1.1 高斯过程

高斯过程(Gaussian process，GP)是把多个维度的高斯在无限维上进行扩展，它是随机性的，高斯过程通过均值函数和协方差来进行定义的。

m(x)=E[f(x)]

(2)

k(x,x′)=E{f(x)-m(x)[f(x′)-m(x′)]}

(3)

式中：m(x)为均值函数；E为期望，k(x,x′)为协方差函数，当x=x′时，k(x,x′)=1，x和x′相差越大，k越趋向于0。

则高斯过程可表示为

f(x)～GP[m(x),k(x,x′)]

(4)

式(4)中：GP为高斯过程(Gaussian process)。

在计算时为了方便，通常将均值初始函数值设为0，当知道{(xi,fi)|i=1,2,…,n}时，则必然有一个高斯分布存在，其中(xi,fi)为第i个函数值，且满足：

f～N[0,K(X,X)]

(5)

式(5)中：N为联合分布；高斯过程的协方差矩阵K(X,X)和协方差函数k(x,x′)可分别表示为

(6)

(7)

因此，加入新样本X*，并利用协方差矩阵生成一个新的高斯分布，可表示为

f*～N[0,K(X*,X*)]

(8)

由高斯过程的性质可得，训练输出f和测试输出f*的联合分布为

(9)

则f*的联合后验分布满足：

f*|X*,X,f～N[K(X*,X)K(X,X)-1f,

K(X*,X*)-K(X*,X)K(X,X)-1K(X,X*)]

(10)

3.1.2 采样函数

通过采样函数可以确定下一个要评估的点，减少重复次数，大大降低优化成本。对采样点函数进行选择时，有两方面需要考虑，一个是利用一个是探索。利用就是利用当前的最优解，在最优解附近寻找下一步的最优解，探索是对未评估过的点进行探索，避免只在局部探索而造成的不全面的搜索。

对于采样函数，常用的有：期望的改进函数EI、改进的概率函数PI以及上限置信区间UCB。本实验选择UCB作为采用函数，函数公式为

UCB(x)=μ(x)+εδ(x)

(11)

式(11)中：μ(x)和δ(x)分别为利用高斯过程并结合后验分布函数得到的均值和协方差；利用式(11)可以对参数ε进行修剪和调节。

3.2 实验验证

将实验数据集中的2012—2017年长时间序列数据为训练集，2018年数据为测试集，将训练集进行训练。并且通过交叉验证确定参数以获得最佳的模型效果。

为了提高预测精度，利用贝叶斯优化对参数进行优化，贝叶斯优化作为调参利器的一种，它是一种黑盒优化算法，用于求解表达式未知的函数的极值问题。算法根据一组采样点处的函数值预测出任意点处函数值的概率分布，这通过高斯过程回归而实现。根据高斯过程回归的结果构造采集函数，用于衡量每一个点值得探索的程度，求解采集函数的极值从而确定下一个采样点。最后返回这组采样点的极值作为函数的极值,优化流程如图5所示。

超参数是进行模型训练时用于控制算法行为的参数。由于这些参数并不能从常规训练中得到。因此在进行训练模型前，需要为它们分配值。

对于随机森林，当“子模型数”的值增加时，它对减少模型的总体方差具有显著作用，但对子模型的偏差和方差没有影响。但是，由于改变是为了减少模型方差公式的第二项，因此提高精度存在上限。在不同条件下，“分裂准则”对模型的准确性有不同的影响，并且在实际使用中需要灵活调整此参数。如果希望模型具有较低的偏差和较高的方差，则需要制作更多的叶节点或树的深度变的更深；同时，通过调整“min_samples_leaf”和“min_weight fraction_leaf”，这意味着子模型结构较为复杂，一般情况下，使用bootstrap进行子采集可以减少样本之间的相关性。在分割过程中，适当减少考虑的最大特征数量“max_features”，或者将其他的随机性考虑到子模型中也能使子模型之间相关程度降低。但是，如果盲目地对此参数进行减少是不行的，因为在拆分过程中的可选功能比较少，因此会导致模型的偏差逐渐增大。图6中，可以看到上述参数对随机森林模型的整体性能的影响。

本实验主要对max_depth、min_samples_leaf、n_estimators、min_samples_split这4个主要参数进行贝叶斯优化以提高预测精度。其中，将max_depth的值设置为None。贝叶斯优化过程主要包括先验函数和采集函数，PF是利用高斯过程来实现的，采集函数包括EI、PI、UCB[18-19]

构建贝叶斯优化改进的随机森林模型使用sklearn库以及scikit-optimization的BayesSearchCV，模型的超参数范围设max_depth[5,15],n_estimators[10,250],min_samples_split[2,25],min_sam-ples_leaf[1,10]。使用sklearn 中的贝叶斯搜索函数对上述函数设置的区间进行搜索，同样以RMSE作为精度评价指标，进行最优参数组合。伪代码如下。

输入:f,x,s,m

输出:一组最近的超参数

1.begin

2.D←initsamples(f,x)

3.fori←|D|toTdo

4.p(y|x,D)←fitmodel(m,D)

6.yi←f(xi)

7.D←D∪(xi,yi)

8.end for

其中，f为所谓的黑盒子，即输入一组超参数，得到一个输出值;T为目标函数；x为超参数搜索空间；s为采集函数；m为对数据集D进行拟合得到的模型；D←initsamples(f,x)这一步骤就是初始化获取数据集D=(xi,yi)，(xi+1,yi+1)，…，(xn,yn)，其中yi=f(xi)，这些都是已知的；每次选出参数x后都需要计算f(x)，因此一般需要固定选参次数(或者是函数评估次数)，p(y|x,D)←fitmodel(M,D)，预先假设M服从高斯分布，且已知了数据集D，因此可通过模型函数表示；xi为一组超参数；yi←f(xi)表示由xi去得到超参数yi；D←D∪(xi,yi)表示更新数据集。

贝叶斯参数优化过程如表2所示。

a表示对模型性能的影响；p表示参数的递增；o为原点坐标图6 随机森林参数对整体模型性能的影响Fig.6 The influence of random forest parameters on overall model performance

可以看出，仅迭代了30次，贝叶斯优化就得到了最优参数组合。

从图7可以看到，在前面15次迭代时，R2变化较大，但是迭代15次后，R2就很稳定，这说明贝叶斯优化已经找到相对较好的参数组合。最后得到最优的参数组合如表3所示。

优化结果显示当4个超参数的值分别取以上值时可以取得最小均方根误差(root mean squared error, RMSE)，将参数 max_depth、min_samples_leaf、min_samples_split、n_estimators取14.43、1.289、2.828、241.3时预测精度最高，编译函数采用fit(·)。

表2 贝叶斯参数优化Table 2 Bayesian parameter optimization

4 网格搜索改进的随机森林模型

4.1 网格搜索技术框架结构

网格搜索即通过对所有的参数进行循环遍历，最终选择使得机器学习模型表现最好的参数或参数组合，也称为“穷举法”，无确定的函数公式与之相照应。它的关键是调优搜索。通过构建参数候选集合，对所有候选参数进行选择时，通过循环尝试各种可能性，具有最佳性能的参数是最终结果，它类似于手动调整。对于连续型的超参数，对其可行域进行网格划分，选取一些典型值进行计算。假设需要确定的超参数有2个，第1个的取值为[0,1]之间的实数，第2个的取值为[1,2]之间的实数。则可以按照如下的方案得到若干离散的取值，以这些值运行算法：将第1个参数均匀的取3个典型值，将第2个参数均匀的取3个典型值。对于所有的取值组合运行算法，将性能最优的取值作为超参数的最终取值，这种方法如图8所示。

网格搜索随着参数数量的增加呈指数级增长，因此对于超参数较多的情况，该方法面临性能上的问题。著名的支持向量机(support vector machine，SVM)开源库libsvm使用了网格搜索算法确定SVM的超参数。

图7 迭代结果曲线Fig.7 Curve of iteration results

表3 最优参数组合Table 3 Optimal parameter combination

图8 网格搜索的原理Fig.8 Principle of grid search

网格搜索的基本原理是，首先设置参数的值范围，然后通过特定步长将参数的可行区间划分为网格，然后通过搜索每个网格将参数的值控制在一定范围内。并根据特定规则搜索所有交点，并以此方式找到每个最佳目标函数的交点。此时，最佳参数是交点处的参数[20-21]。

当径向基函数(rodial bosis function, RBF)的核函数选择后，惩罚因子C和核函数参数σ也要确定，以提高故障识别率。在网格搜索方法中，惩罚因子C的间隔为C∈[C1,C2](其中，C1为惩罚因子最小值，C2为惩罚因子最大值)，其改变步长为CS，核函数参数的间隔为σ∈[σ1,σ2](其中，σ1为核函数参数最小值，σ2为核函数参数最大值)，其改变步长为σS。网格搜索方法对网格区间中的每对参数(C′,σ′)执行模型训练和故障识别率计算，最后把识别率最高的参数作为模型的参数。网格搜索实际上是一个n层循环(n为参数的数量)，其计算步骤如下。

步骤1初始化精度为0和参数C,σ的初始值C1、σ1。

步骤2固定步长C增长CS,C=C+CS。

步骤3固定步长σ增长σS，σ=σ+σS。

步骤4引入参数(C,σ)建立支持后量机(support vector machine,SVM)模型，使用测试样本计算预测准确率，与上一步准确率的进行比较，如果准确率得到提高，则将该参数C、σ替换上一步C、σ，反之亦然。

步骤5判断σ是否增加到σ2,如果是，则跳至步骤6；如果不是，则执行步骤3。

步骤6判断C是否增长到C2,如果是则执行第7步,如果不是，则执行第2步。

步骤7当前C和σ作为为最优参数,计算结束。

通过上述循环找到RBF函数的最佳参数之和就足够了。

4.2 实验验证

为了对预测算法的精度进行提高，需要对参数进行优化，提出一种基于袋外数据估计的回归误差，采用改进的网格搜索算法对随机森林(random forest,RF)模型进行参数调优，流程图如图9所示。设随机森林树的数量为n_estimators, 范围设置为[50,100,150,200],树的高度为max_depth, 范围设置为[3,4,5,6],拆分内部节点所需的最小样本数为min_samples_split,范围设置为[2,3,4,5]。叶子节点所需的最小样本数为min_samples_leaf,范围设置为[1,2,3,4]。采用网格搜索算法根据步长对参数进行依次调整，对参数范围依次遍历找到使精度最高的参数，并利用5折交叉验证对其进行评估。5折交叉验证是通过将数据集平均分为5份，随机选择4份作训练集，1份作测试集，一共进行5次训练和测试，采用精度等评分方法计算平均值，然后找到评分最大的参数组合，得到预测精度最高的一组最优参数。

考虑到随机森林算法中决策树数k′和候选分裂属性数mtry为离散值，提出的基于网格搜索改进的随机森林模型进行参数优化时目标函数值选用袋外数据估计误差。随机森林模型在构建过程时存在随机性，回归误差也会在一定范围内存在波动，因此为减小不确定性对参数选择的影响，在计算回归误差时选取多个结果的平均值作为随机森林模型回归误差。当搜索完毕时输出最优参数，其搜索过程用流程图(图10)来表示。

构建网格优化改进的随机森林模型采用sklearn库中的sklearn.ensemble模块，从模块中调用RandomForestRegressor函数对参数进行网格优化，模型的超参数及范围设置如表4所示。在本次实验中，它总共构建了256个不同的模型。

图9 优化的随机森林算法整体流程Fig.9 Overall flow of the optimized random forest algorithm

图10 基于改进的网格搜索算法的随机森林参数寻优流程图Fig.10 Flow chart of random forest parameter optimization based on improved grid search algorithm

在利用网格搜索算法对随机森林模型进行改进时采用的函数是sklearn中的grid search函数[sklearn.Model_selection.GridSearchCV()]，通过对上述设置的区间范围进行搜索，以寻求模型精度最大时的最优参数组合。各参数与结果表现关系如图11所示。图11(a)为树的最大深度与拟合优度R2的关系，图11(b)为叶子节点所需的最小样本数与拟合优度R2的关系，图11(c)为拆分内部节点所需的最小样本数与拟合优度R2的关系，图11(d)为随机森林树的数目与拟合优度R2的关系。

表4 设置需要调整的参数及范围Table 4 Set the parameters and ranges that need to be adjusted

test_score表示模型精度即拟合优度R2图11 各参数与结果关系图Fig.11 Relationship between parameters and nesults

调参结果显示当n_estimators，min_samples_split，max_depth，min_samples_leaf′的取值分别为150、2、6、1时可以得到最小均方根误差(root mean squared error,RMSE)和最大的拟合度R2值，将参数调整后的最优参数组合输入模型，使用predict函数来预测。此时得到的最优R2值为0.961 8，RMSE值为0.039 5，平均绝对误差(mean absolute error，MAE)值为0.021 6。

5 结果与分析

模型预测性能对比分析如表5所示。经过贝叶斯优化和网格优化后的R2分别从0.951 0提高至0.975 3和0.961 8，同时参考其他几个评价指标，都显示预测效果有明显提高。其中基于贝叶斯优化改进随机森林模型预测精度最高，且有明显提高，均方根误差值也最小。预测结果对应的柱状图如图12所示。

表5 模型预测性能对比分析Table 5 Comparative analysis of model prediction performance

图12 改进前后模型预测对比柱状图Fig.12 Histogram of comparison of model predictions before and after improvement

可以看出，网格优化改进随机森林模型后运行时间T由原来的4.95 s提高至3.23 s。贝叶斯优化改进随机森林模型后运行时间由原来的4.95 s提高至3.12 s，比网格优化提升更高且参数搜索范围大大增加。

为了更形象生动的比较上述算法的预测精度，将改进前后的3种模型的预测结果与真实值进行比较，如图13所示，可以看出，基于贝叶斯优化和网格优化调整超参数改进后的模型的预测结果基本和零误差线y=x重合，说明贝叶斯优化改进的随机森林模型和网格优化改进的随机森林模型预测的结果和真实值基本一致；其预测精度在所有算法中达到最大。

图13 不同模型测试集真实值与预测值相关性Fig.13 Correlation between the true value and the predicted value of the test set of different models

6 结论

采用机器学习算法并结合NPP/VIIRS夜间灯光数据进行长三角地区GDP的智能预测研究，通过对数据集的一系列处理，对随机森林算法进行了贝叶斯优化和网格搜索自动调参，对算法中的超参数调优，该优化方法将预设的模型参数自由组合，对所有参数组合进行遍历搜索，通过对3种指标的分析，比较不同模型的特征并对模型进行评估。结果表明，预测效果最好的是贝叶斯优化改进的随机森林模型，R2达到了0.97，优化后的随机森林模型有明显提高。后续的研究可以围绕着扩展模型的训练样本集、采用更长年限的长时间序列数据集、改进目前使用的模型等方面进一步开展，促使模型更加健壮和可靠。