开关磁阻电机结构优化设计及其三维图解法

邹声奇， 陈亮亮， 伍家驹， 杨声云， 刘宇轩， 钟旺

(南昌航空大学信息工程学院， 南昌 330063)

开关磁阻电机(switched reluctance motor，SRM)作为一种新型的、高效节能的机电一体化产品，具有结构简单、坚固耐用、工作可靠、制作成本低和功率电路简单可靠等诸多优点，使其在电动车、机床、风机、水泵、纺织、锻压和城市交通等领域得以广泛应用[1-4]。但是，开关磁阻电机的双凸极结构和开关式供电方式决定了其固有缺点，边缘磁通效应会引起电流非线性变化，转子转矩由脉冲转矩合成，不是恒定值，导致了电机固有的转矩脉动，限制了其在高精度运行场合下的应用[5-7]。

转矩脉动的抑制技术主要分为两类：一是对电机本体结构进行优化设计；二是采用先进的电机控制策略。陈吉清等[8]利用NSGA-II(non-dominated sorting genetic algorithms)算法在集成优化平台上对电机结构进行多参数、多目标优化，得到电机结构参数对转矩脉动的影响规律；陈飞等[9]分析了定转子极弧和定转子轭高对电机转矩的影响，得到了电机参数的优选值；臧涛等[10]采用优化函数定量分析了结构参数对电机性能的影响，提供了电机设计和优化的新思路；张鑫等[11]在转子齿两侧开槽，削弱转子表面的径向磁密，减小了电机的电磁振动；孙会琴等[12]建立了电磁转矩与气隙长度的分析模型，指出定子斜齿结构可以有效减小转矩脉动；蔡燕等[13]优化了T形转子齿，减小了电机的径向力波，增加了切向力波，使电机转矩脉动减小；黄朝志等[14]在分段转子开关磁阻电机的定子槽口上增设永磁体，形成混合励磁，提高平均转矩的同时减小了转矩脉动；Hosseini等[15]提出了梯形定转子极形状，并根据应力分析进行结构改造，降低了电机运行时的噪声。

在控制策略抑制转矩脉动的研究方面，Hamouda等[16]提出了一种改进的电动汽车用开关磁阻电机直接瞬时转矩控制(direct instantaneous torque control，DITC)策略，该策略具有转矩脉动小、转矩电流比大等优点；王云刚等[17]对直接转矩控制进行了改进，通过空间电压矢量的控制进而控制转矩，解决传统直接转矩控制起动转矩脉动大的问题，使系统运行时有更好的动态性能；卿龙等[18]提出了一种能够有效抑制转矩脉动的控制策略，该控制策略将开通角选择、导通相选择、提前关断前一相等方法相结合；周凯等[19]提出了模糊比例积分(proportional-integral，PI)直接转矩控制，有效地抑制了电机转矩脉动，且使电机具有较好的动态响应；党选举等[20]提出了电流优化分配与迭代学习相融合的综合控制策略，有效降低了转矩脉动；蔡辉等[21]提出了一种无差拍电流预测方法，提高了电流跟踪特性，减小了转矩脉动；许爱德等[22]提出了一种基于脉宽调制的直接瞬时转矩控制策略，对转矩脉动进一步优化。在对电机本体结构的优化设计中，学者们提出了许多特殊结构，但对结构参数进行多目标约束寻优方面的研究尚鲜有提及。

为此，从开关磁阻电机本体结构出发，研究了定子磁极结构对平均转矩和转矩脉动的影响，提出一种在定子磁极端部具有楔形角的电机结构，分析了该楔形结构中各参数对电机平均转矩及转矩脉动的影响，并利用多维数据可视化的方法对结构参数进行多目标约束寻优，得到最佳参数值，采用有限元电磁仿真软件进一步验证了设计方案的有效性。

1 转矩脉动分析

开关磁阻电机在运行时遵循“磁阻最小原理”，即磁通总是沿着磁阻最小的路径闭合。其双凸极结构导致定子磁极和转子磁极在交叠前产生边缘磁通效应，进而引起电流的非线性变化。因此，磁链对转子位置角θ和相电流i具有非线性关系，电磁转矩Te也随之而呈现非线性关系，电磁转矩由一系列脉冲转矩所合成，必然会存在转矩脉动。

(1)

式(1)中：W′为磁共能，J；i1为第一相绕组电流；i2为第二相绕组电流；im为第m相绕组电流。

转子位置角θ的改变会引起定转子间气隙变化，而旋转电机的磁场能量主要储存在气隙里，定转子磁极开始进入重合区域时，气隙长度骤降，气隙磁场能量随之突变，引起转矩值降低，在换相点处转矩值最小，使合成转矩出现明显波动。

减小气隙突变可改善转矩脉动，在定子磁极端部两侧加入楔形结构，气隙长度变化趋于缓慢，从而减小气隙磁场能量突变。磁极端部两侧的楔形结构会增大定子磁极的极弧系数，限制相电流幅值，使平均电磁转矩降低，因此，需要对楔形结构尺寸进行优化设计。

2 楔形结构及原理分析

提出一种图1所示的楔形结构，这是一个定子磁极的右端部分，直线AE以左的部分为原来的磁极，封闭曲线ABCDEA组成的图形即为特殊楔形结构。AB与线段EA垂直，设AB段长度为l，单位：mm；BC和DE为圆弧，半径分别为R和r，单位：mm；AB和DC延长线的夹角为α，单位：°，使得该特殊楔形结构的大小和形状被完全约束。该特殊楔形结构还可用于固定槽内线圈，具有槽楔的功能，为防止R和α取值较小时形状过于宽扁而导致强度较低，限定R=0.5l。

图1 特殊楔形结构Fig.1 Special wedge structure

根据开关磁阻电机单相导通时的线性模型假设，在电流i为恒值时，式(1)可以简化为

(2)

(3)

式(3)中：ψ为磁链，Wb；L为电感，H。

将式(3)代入式(2)得

(4)

式(4)中：θc为导通角，°；Lmax和Lmin分别为最大电感和最小电感，H。

不难发现，在电流和导通角一定的情况下，电磁转矩的大小取决于电感的变化量。在开关磁阻电机中，电感值与铁芯材料的磁导率、绕组匝数及横截面积、定转子磁极大小、铁芯叠长、气隙结构等因素有关。电感L与磁阻Rm成反比关系，即L∝(1/Rm)。因电机中铁芯材料的磁导率远大于空气的磁导率，气隙磁阻远大于铁芯磁阻，使大部分磁压降发生在气隙中，因此，这里主要考虑气隙磁阻，所以磁阻Rm=le/(μ0Ae)，其中le为等效磁路长度，单位：m；Ae为绕组截面积，单位：m2；μ0为空气磁导率，μ0=4π×10-7H/m。图2为传统电机结构与所提出电机结构在最小电感处的磁路模型，楔形结构的加入，空气隙减小，相当于等效磁路长度减小，使得最小电感值增大。图3为两种电机结构在最大电感处的磁路模型，可以看出，在最大电感位置时，楔形结构改变了磁路方向，致使部分磁路长度加大，同时漏磁增大，使最大电感值减小。根据式(4)可知，在电流和导通角不变的情况下，由于楔形结构的加入，电感值的变化量减小，电磁转矩也将随之降低。

图2 两种电机结构在Lmin位置时的磁力线Fig.2 Magnetic force lines of the two motor structures at Lmin position

图3 两种电机结构在Lmax位置时的磁力线Fig.3 Magnetic force lines of the two motor structures at Lmax position

3 楔形结构参数的优化设计

3.1 结构参数对转矩的影响

楔形结构能够补偿换相点位置附近的转矩值，但其结构参数对电机转矩脉动和平均电磁转矩的影响各不相同。开关磁阻电机的电磁环境复杂，用解析法计算磁场有较大难度，这里采用有限元软件进行仿真分析。以一台6/4极电动摩托车用开关磁阻电机为研究对象，额定电压72 V、额定功率4 kW、额定转速9 000 r/min，其定转子结构参数如表1所示。

为了定量评价电机的转矩脉动，定义转矩脉动系数为

(5)

式(5)中：Tmax为电机稳定运行时的最大转矩，N·m；Tmin为最小转矩，N·m；Tav为电机稳定运行时的平均电磁转矩，N·m。

转矩脉动系数越大表明电磁转矩波动越大。图4是以表1为基本结构参数建立的二维有限元仿真模型，让该模型在额定转速下进行瞬态场有限元仿真，触发角和脉冲宽度分别为0°和120°，该值是转子位置角θ的4倍，因此，所对应的开通角和关断角为0°和30°，达到稳定状态时输出转矩随时间变化的曲线(图5)。

表1 电机的主要结构参数Table 1 Main structure parameters of the machine

图4 SRM二维仿真模型Fig.4 SRM 2D simulation model

t为时间图5 基本结构模型转矩曲线Fig.5 Torque curve of basic structure model

由转矩曲线(图5)可知，平均电磁转矩为5.38 N·m，最大转矩为11.04 N·m，最小转矩为1.46 N·m，并根据式(5)计算转矩脉动系数k=1.78。

在有限元软件中建立具有楔形结构的定子模型较为困难，楔形结构参数难以把控，因此，先在三维建模软件中制作具有楔形结构的定子模型，并导入二维有限元软件中进行电磁仿真。所提特殊楔形结构具有4个参数，分别是图1中AB段长度l、BC段和DE段的圆弧半径R和r、AB和DC的夹角为α，其中R的取值受限于l。楔形角形状大小不宜过大，即该4个参数取值不宜过大。保持r=0.3 mm，α=30°不变，对l由0.1 ～1 mm的优化范围，步长为0.1 mm的模型进行有限元瞬态分析，由于R=0.5l，此时的R取值由0.05 ～ 0.5 mm变化，得到仿真结果如图6(a)所示。

分析可知，随着l和R的增大，平均转矩Tav在不断减小，转矩脉动系数k从整体上看也呈现下降趋势。因为l和R的增大，都会使极弧系数加大，限制相电流，从而使电磁转矩Tav下降。l和R取值较大时，转矩下降较快。因此，在设计该楔形角时，l和R的选值不宜太大。

为考虑半径r和夹角α的影响，图6(b)、图6(c)分别给出了r和α对转矩脉动影响的有限元瞬态仿真结果，在图6(b)中，选用的楔形结构参数l=1 mm，R=0.5 mm，α=30°，r由0.1 ～1 mm逐渐变大，图6(c)中楔形结构参数l=1 mm，R=0.5 mm，r=0.3 mm，α由25°～50°逐步变化。

图6 l、R、r和α对Tav和k的影响曲线Fig.6 Influence curvess of l, R, r and α on Tav and k

由图6(b)可知，r的取值对平均电磁转矩的影响较小，对转矩脉动系数的影响无明显规律，r为0.3 mm和0.5 mm时，转矩脉动系数达到一个较低点。由图6(c)可知，随着α值的增大，平均转矩逐渐减小，α在30°～40°有较小的转矩脉动。

3.2 可视化寻优

由于DE段的圆弧半径r的取值对平均电磁转矩的影响很小，因此，选取r=0.3 mm时平均电磁转矩较大、转矩脉动较小的点，通过有限元仿真进一步研究AB段长度l和AB与DC的夹角α两个参数共同作用下转矩脉动的变化规律，对l的取值范围为0.2～1 mm，α的取值范围为25°～50°的所有参数组合扫描仿真，得到不同参数组合下的平均电磁转矩和转矩脉动系数。在此基础上，采用三维数据可视化算法，其中l和α为两个自变量维度，因变量的色谱图为第三维。将平均电磁转矩和转矩脉动系数的值域与计算机色谱图相对应，得到图7所示的可视化数据图。

图7表明，随着l的增大，平均电磁转矩与转矩脉动逐渐减小，当保持l不变时，减小α角，可以提高平均电磁转矩，l在一定范围内，适当减小α值，可以降低转矩脉动。l和α对电机性能影响不尽相同。根据电机的额定参数计算额定转矩，其计算公式为

(6)

式(6)中，T为额定转矩，N·m，取4.24 N·m；P为额定功率，W；n为额定转速，r/min。

因此，在对电机进行优化设计时，约束条件①是平均转矩值须大于4.24 N·m，由图7(a)可知，任意一点都符合该约束条件；约束条件②是转矩脉动须小于传统结构的80%，即剔除图7(b)中k值大于1.42的点，剩余的点则符合约束条件②，如图8所示。

在设计l和α的参数时，须同时满足平均转矩和转矩脉动的约束，因此，对图7(a)和图8中分别满足单个条件的取值范围进行求交运算，得到满足两个约束条件的取值范围，所求得交集无法直观表达平均转矩和转矩脉动系数的变化趋势，如图9所示。

至此，求取了所有满足要求的全部取值范围。为了方便表示优化后的效果，定义平均电磁转矩与转矩脉动的比值为优化目标u，单位：N·m，可表示为

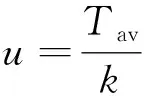
(7)

根据式(7)计算取值范围内的优化目标u，用可视化算法得到u和l、α的色谱图如图10所示。

由式(7)可知，u的值越大，优化效果越好。图10直观表达了优化效果u与楔形结构参数l和α的关系，根据u的取值可以直接方便的选择结构参数。观测可知，中间区域u值较大，且颜色相近，在此范围内选取l和α值，能够使所选值具有较好的稳定性和鲁棒性。

图8 符合约束k的取值范围Fig.8 The value range that meets the constraint k

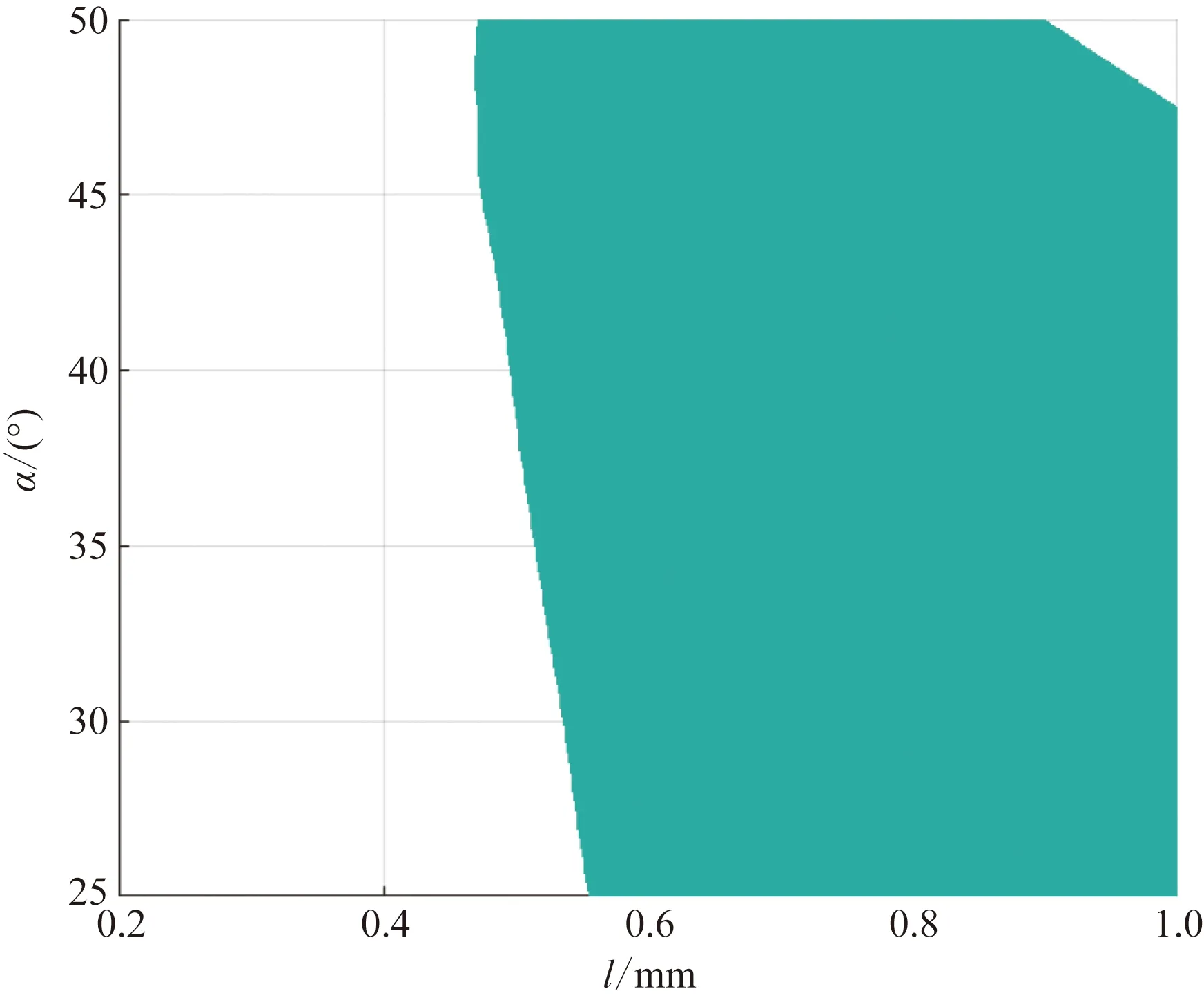
图9 满足两个约束的取值范围Fig.9 Meet the scope of two constraints

图10 l和α对优化效果u的影响Fig.10 Influence of l and α on optimization effect u

4 仿真分析

根据图10的优化结果，选取特殊楔形结构参数l=0.8 mm，α=40°，R=0.4 mm，r=0.3 mm为特殊楔形结构的最终参数，优化前后的结构对比以及局部示意图如图11所示。对最佳优化结构进行有限元瞬态仿真分析，将优化结构的仿真结果与基本结构仿真结果进行对比，对比结果如表2所示。

由表2可知，优化后转矩为4.86 N·m，保持在原来的90%以上，转矩脉动系数下降到1.30，为原来的73.2%，下降了26.8个百分点，优化电机结构的两个指标都符合上文所设的约束条件，且在所选的楔形结构参数附近，都具有较好的优化效果。

图11 优化前后电机结构及局部放大图Fig.11 Optimized front and rear motor structure and local enlarged drawing

表2 优化前后仿真结果对比Table 2 Comparison of simulation results before and after optimization

5 结论

(1)提出了一种新型定子结构，在定子磁极端部两侧加入一个特殊楔形结构，该楔形结构可以形成过渡气隙，有效抑制转矩脉动。

(2)在特殊楔形结构中，不同的结构参数对电机性能有不同的影响，其中，l和R对平均电磁转矩和转矩脉动系数有较大影响，l和R的取值越大，平均电磁转矩和转矩脉动越小；r对平均转矩影响较小；α在30°～40°对转矩脉动有较好的抑制作用。

(3)所提出的基于多维数据可视化算法的优化方法可用于电机结构参数的寻优，能够得到设计参数的最优参数集，增加了参数的选择范围，具有计算量小、直观、方便的特点。