基于压缩感知和小波信息熵的滚动轴承特征提取方法

李中， 王星， 卢春华

(1. 华北电力大学电子与通信工程系， 保定 071003; 2. 华北电力大学河北省电力物联网技术重点实验室， 保定 071003)

滚动轴承在工业领域应用广泛，在线监测诊断分析其运行状态十分重要。基于 Nyquist-Shannon 采样定理的传统采样方法,采样的频率要求远远大于故障状态下信号的最高频率两倍,而故障状态下的滚动轴承振动信号的高频分量会增加，这给在线监测和故障诊断过程中的信号采集、传输、存储和处理提出了更高的要求。Donoho[1]提出了压缩感知技术，采集少量信号即可包含传统采样信号的大部分信息，为解决这一问题提供了新的思路。

中外学者就振动法分析诊断轴承运行状态做了大量研究工作。Min等[2]根据小波包分解后的能量分布构造特征向量，确定滚动轴承故障的类型和严重程度。陈宗祥等[3]分析比较了不同状态下经小波包分解后各子频带信号能量分布并结合小波包重构和Hilbert解调技术判断滚动轴承的故障位置。陈湘中等[4]以小波包分解的各节点能量作为特征参量，提出基于蚁群优化的K均值聚类算法识别故障类型。苏文胜等[5]利用小波包分解求取最大能量自带的样本熵，将此样本熵作为故障诊断的特征参量。张龙等[6]利用加权能量算子对小波包分解最优系数的节点解调分析信号的瞬时能量，最后分析包络谱频率成分判断故障类型。陈慧等[7]应用局部均值算法对最优小波系数加权运算增强滚动轴承的冲击部分。Wang等[8]采用滑动均值滤波算法对原始数据作预处理，将平滑后的数据作为故障诊断的输入向量。冯桓榰等[9]应用小波包分解提取振动信号小波包熵作为轴承特征参量。Verstockt[10]基于卷积神经网络的状态监测特征学习模型从数据本身中自主提取轴承故障特征，然后在Hilbert解调谱中提取特征频率判断轴承的运行状态。这些成果基于各种信号处理和机器学习等技术，较好解决了滚动轴承振动信号的特征提取和故障诊断问题，但没有对振动信号进行压缩处理，其监测和诊断过程存在成本高、耗时长等不足。

针对振动信号监测分析中应用压缩感知技术的研究主要包括：一是振动信号的压缩与重构；二是基于重构信号提取特征进行故障诊断。刘畅等[11]以幅值百分比作为阈值对稀疏系数进行稀疏处理，采用高斯随机测量矩阵实现滚动轴承振动数据的压缩。唐其琯等[12]根据信号频域稀疏特性设计一种确定性随机观测矩阵，采集的滚动轴承振动信号能以较高精度恢复重构。何天远等[13]在信号的稀疏分解中基于K-奇异值分解生成字典，增加了重构信号和原始信号的相似度。王海明等[14]用快速谱峭度确定最优滤波器参数，在傅里叶稀疏基下对去除噪声的信号包络信号进行重构，分析重构信号频谱判断轴承状态。王江萍等[15]通过高斯随机测量矩阵采集齿轮振动信号，经正交匹配追踪(orthogonal matching pursuit，OMP)算法重构信号，从重构信号的Hilbert解调谱中提取特征频率判断齿轮的运行状态。

综上所述，现有应用压缩感知理论采集滚动轴承振动信号实现在线监测和故障诊断有关研究中，存在重构计算复杂且难免产生新的误差，影响故障诊断精度的问题。考虑大多状态下正常信号高精度重构对监测和故障诊断意义不大，现提出直接提取压缩后的滚动轴承振动信号特征进行故障诊断，提取压缩信号的归一化小波信息熵作为故障诊断的依据。该方法首先利用部分哈达玛(PartHadamard)测量矩阵完成对振动信号的压缩，应用小波包分解压缩信号得到各子频带的小波信息熵，将各子频带归一化小波信息熵作为故障诊断的特征参量。在标准数据集上，应用粒子群优化的支持向量机(particle swarm optimization-support vector machine, PSO-SVM)、K近邻(K-nearest neighbor, KNN)、决策树(decision tree, DT)、概率神经网络(probabilistic neural network, PNN)4种分类算法完成了滚动轴承故障诊断实验。

1 压缩感知和小波包分解

1.1 压缩感知

压缩感知的数学模型为

y=ΦMlength×NΨθ

(1)

式(1)中：y为采集的压缩信号；Φ为Mlength×N的测量矩阵；Ψ为原始信号的变换基；θ为信号在变换基下稀疏分解的系数；N为原始信号长度；Mlength为压缩信号的长度，原始信号本身稀疏或在变换基Ψ下可以稀疏表示。

在满足压缩感知的数学模型的所有条件中，求取最稀疏解为求解最优化问题。

(2)

式(2)中：x为原始信号；‖x‖0为原始信号的L0范数。

求解最优解问题是一个非确定性多项式难题(non-deterministic polynomial hard, N-hard)问题，引入约束等距(restricted isometry property, RIP)性质，可表示为

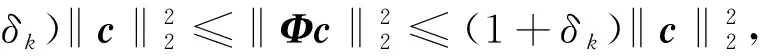
0<δk<1

(3)

式(3)中：c为稀疏信号；δk为原始信号稀疏分解后的稀疏度。

在测量矩阵Φ满足RIP性质的情况下，可以将求解L0范数问题转化为求取L1范数问题，通过求取L1范数可以恢复出稀疏信号。

(4)

式(4)中：‖x‖1为原始信号的l1范数。

1.2 小波包分解

小波包分解可以在低频和高频完成对信号的分解，相比小波分解小波包分解有更高的频率分辨率。小波包分解算法的递推公式可表示为

(5)

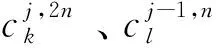
小波包重构算法计算公式为

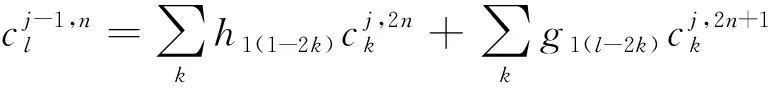
(6)

式(6)中：h1(l-2k)、g1(l-2k)分别为低通滤波器系数、高通滤波器系数。

通常情况下，小波包分解提取模式特征需要考虑两个问题：一是小波基函数的选择；二是分解层数的确定，层数过少难以提取信号的故障细节信息，层数过多则计算复杂、提取特征维度高，传输和存储开销大。

2 基于压缩感知和小波信息熵的滚动轴承振动特征提取

所提出的滚动轴承振动信号特征提取方法，包括信号压缩和特征选择两个基本环节：首先构造并应用PartHadamard测量矩阵完成振动信号的压缩，然后对压缩信号进行db5小波包分解，选择归一化小波信息熵作为滚动轴承振动信号特征。

2.1 构造测量矩阵

测量矩阵的选择直接决定了采集的振动信号，采集的振动信号是否包含原始信号的大部分信息是衡量测量矩阵的重要准则，硬件设计能否易于实现是评判观测测量矩阵的重要标准。根据压缩感知理论，测量矩阵决定了获取的压缩信号，对基于压缩信号的提取特征具有重要影响。构造满足RIP性质的测量矩阵，才能保证获取的压缩信号包含原始信号大部分信息，满足特征提取和后续故障诊断的需求。其次，还需考虑软硬件成本和实现难易程度。

考虑PartHadamard矩阵满足式(3)中所示的约束等距性质[16]，并且PartHadamard矩阵是由±1组成的正交矩阵，信号采集只涉及加减运算，易于硬件实现[17]，选取PartHadamard矩阵作为测量矩阵。构造PartHadamard矩阵需要借助哈达玛(Hadamard)矩阵，选取Hadamard矩阵的前M′行向量构成测量矩阵。Hadamard矩阵构造过程如下。

最低阶的Hadamard矩阵为二阶Hadamard矩阵，其表达式为

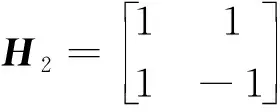
(7)

四阶Hadamard矩阵为

(8)

N阶Hadamard矩阵为

(9)

2.2 db5小波包分解

由于采集的轴承故障信号包含很多冲击成分，对滚动轴承振动压缩信号小波包分解采用db5小波基函数[18]，通过滚动轴承故障信号的特征频率分析确定分解层数[19]。具体方法是：首先计算滚动轴承各种故障状态的故障频率，然后求取滚动轴承振动信号的最佳分解层数J，其表达式为

(10)

式(10)中：fs为采样频率；f为故障频率。

2.3 特征选择

压缩后的滚动轴承振动压缩信号经J层小波包分解后，在频域内被平均分解成2J个子频带，且每个子频带互不重叠，分解后得到2J个小波包系数，基于最后一层小波包分解每个子频带的小波包系数得到每个子频带包含的信号能量，根据每个子频带信号的能量比值得到每个子频带的小波信息熵，小波信息熵能够反映滚动轴承运行状态的不确定程度。将计算获取的小波信息熵归一化作为提取滚动轴承的特征参量，完成特征提取。轴承发生不同故障状态产生的振动信号不同，在频域内经小波包分解后的小波包系数不同，进而得到的归一化小波信息熵也不同，得到的归一化小波信息熵可以作为滚动轴承振动特征。归一化小波信息熵的具体计算过程如下。

设第J层每个子频带的小波包系数分别为CJ(0)，CJ(1)，…，CJ(2J)。每个子频带的能量为

Ei=|DJ(k)|2

(11)

式(11)中：i为子频带编号，i=1,2,…,2J；k为小波系数的编号，k=1,2,…,2J，i和k一一对应；DJ为信号被分解后第k个子频带对应的小波系数数值。

第J层子频带的总能量为

(12)

第J层子频带的能量分布概率为

(13)

第J层每个子频带的小波信息熵为

Si=-PilgPi

(14)

归一化小波信息熵为

(15)

式(15)中：minSi为第J层中子频带的最小小波信息熵；maxSi为第J层中子频带的最大小波信息熵。

3 实验

选择美国凯斯西储大学(Case Western Reserve University, CWUR)电气工程实验室滚动轴承数据集进行数据压缩、特征提取和故障诊断实验，分析检验本文方法的可行性和有效性。

3.1 实验数据

CWUR数据中的滚动轴承型号为SKF6205，轴承分别在内圈故障、外圈故障、滚动体故障和正常4种状态下工作，以12 kHz的采样频率测量采集振动信号。选取滚动轴承空载条件下，故障尺寸直径为0.177 8 mm的滚动轴承振动数据作为本次仿真的实验数据集，4种状态下均包含120个样本，每个样本有768个采样点，实验数据集中滚动轴承转速等其他参数如表1所示。4种状态下的振动数据波形示例如图1所示。

表1 滚动轴承参数Table 1 Rolling bearing parameters

3.2 实验过程与结果

实验仿真包括构造不同PartHadamard测量矩阵压缩振动信号、不同分解层数的特征提取和不同分类器的故障诊断，从压缩性能和诊断精度两个方面分析本文方法的整体性能。在实验数据集上，在相同压缩率下，分别采用不同构造方式的测量矩阵完成滚动轴承振动信号的压缩，用以检验不同测量矩阵构造方法的压缩性能。

然后完成压缩信号的特征提取，采取不同的小波包分解层数来检验特征选择的优劣。最后，基于每种状态下特征提取后实验数据的50%作训练样本，另外50%作测试样本，分别采用PSO-SVM、KNN、DT和PNN4种分类算法进行故障诊断实验，分析检验特征提取后在故障诊断中的精度。

首先进行不同测量矩阵构造方法的实验仿真。测量矩阵的大小取决于信号的压缩率，设压缩率a=(Mlength-N)/N，其中M为压缩信号每个样本的数据长度，N为原始信号每个样本的数据长度。PartHadamard测量矩阵由Hadamard矩阵的M′行向量构成，选取M′行向量的方式有多种：选择前M′行向量、后M′行向量、选偶数行向量、选奇数行向量等。偶数行选取方式：如果选择的偶数行大于要求的采样点数，就继续从偶数行中挑选偶数行；如果选择的偶数行小于要求的采样点数，就在剩余的奇数行中选择偶数行补充[20]。选奇数行和选偶数行的方式类似。分别应用4种方法构成的PartHadamard矩阵采集滚动轴承振动信号。由于PartHadamard矩阵需要满足：行数是2的整数次幂、被12整除后是2的整数次幂、被20整除后是2的整数次幂中的某一个条件，所以测量点数Mpoint不是连续的。

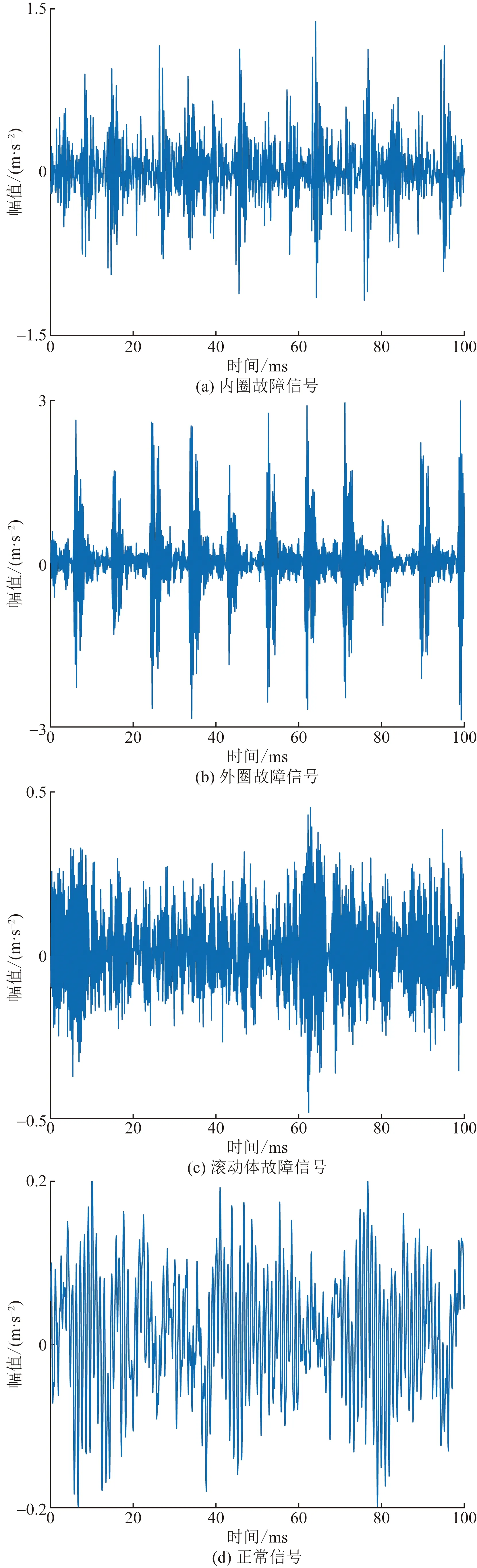
图1 不同状态下的滚动轴承信号Fig.1 Rolling bearing signals in different states

在选择测量矩阵中，用小波包三层分解提取归一化小波信息熵作为故障诊断的输入向量。分别采用SVM、KNN(K=1)、DT和PNN分类方法进行故障诊断仿真，实验结果依次记录如表2所示。

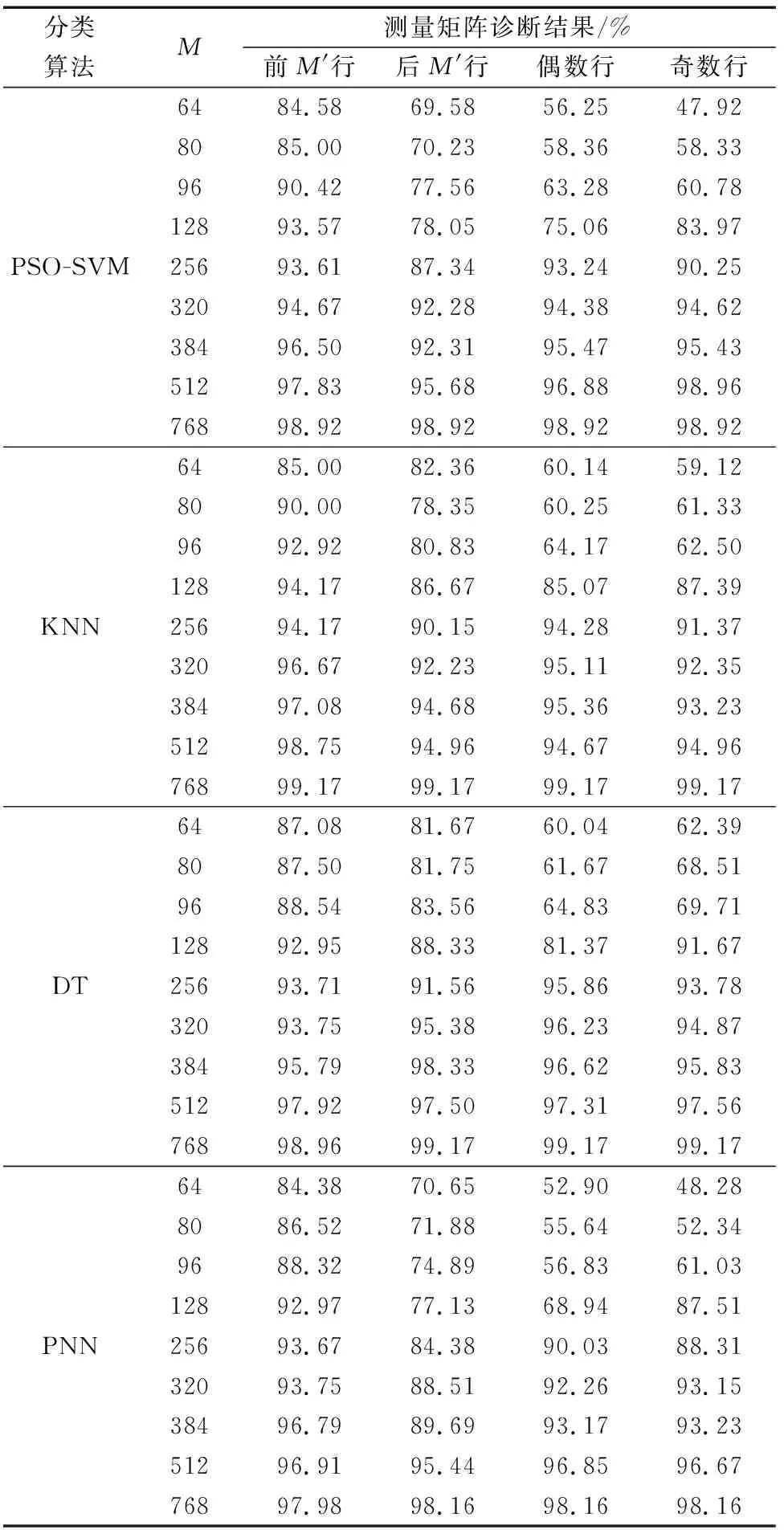
表2 基于不同测量矩阵的诊断结果Table 2 Diagnosis results based on different measurement matrices

实验结果显示，在选择Hadamard矩阵前M′行向量构造测量矩阵时，得到的压缩信号在故障诊断中准确率显著优于其他三种构造方法。在测量点数为128时，其他三种构造方法采集的信号，在故障诊断中准确率明显降低。所以PartHadamard测量矩阵选择Hadamard矩阵前M′行向量。

然后对压缩信号特征提取，考虑到信号经小波包不同层数分解得到的特征参量和特征维度不同，导致故障诊断结果和计算时间不同。需要根据滚动轴承振动信号确定小波包最佳分解层数，分析确定压缩信号小波包最佳分解层数需要考虑滚动轴承各状态的故障频率，实验数据集中3种故障状态的故障频率计算方法如下。

内圈故障频率计算公式为

(16)

外圈故障频率计算公式为

(17)

滚动体故障频率计算公式为

(18)

式中：r为被测滚动轴承的转速；n为滚动轴承滚珠个数；d为轴承滚珠直径；D为轴承节径；α为轴承滚珠接触角。

根据表1，由式(10)和式(16)～式(18)计算得出内圈故障、外圈故障和滚动体故障的小波包最佳分解层数依次分别是小于4、小于4和小于5，综合分析最佳分解层数取3。

为进一步对比分析压缩后振动信号基于不同小波包分解层数的特征提取性能。分别进行压缩数据的2层小波包分解、3层小波包分解和4层小波包分解，提取滚动轴承压缩信号的特征，继而应用PSO-SVM、KNN(K=1)、DT和PNN 4种分类算法进行故障诊断。不同分解层数特征提取的故障诊断结果记录如图2所示。

由图2可知，基于3层小波包分解的特征提取的故障诊断准确率普遍高于2层和4层小波包分解，在相同压缩率下的故障诊断准确率最高。再考虑分解层数与特征参量的维度关系，4层小波包分解得到的是16维特征参量，3层小波包分解得到的是8维特征参量，3层小波包分解在特征提取和故障诊断中相比4层小波包分解降低了特征参量的存储空间和节约了计算时间。本文方法兼顾了故障诊断精度和计算复杂度，特征提取性能优异。

为进一步检验本文方法的性能，对比文献[21]，

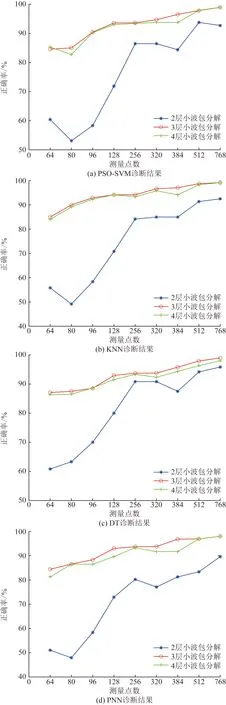
图2 不同分类方法的故障诊断结果Fig.2 Fault diagnosis results of feature extraction with different decomposition levels

在相同数据集上应用本文方法进行特征提取、相同比例训练集和测试集、采用相同的PSO-SVM算法进行故障诊断实验。文献[21]通过计算原始信号和压缩信号的13种敏感特征参量，选取压缩前后特征参量变化不大的方差、峭度因子、波形因子作为故障诊断的输入向量。诊断结果对比如表3所示。

可以看出，在相同压缩率条件下，用本文方法相比文献[21]，可以获得更高的故障诊断精度。为分析本文方法对不同分类算法的普适性，基于上述提取特征和相同的训练集与测试集划分方法，分别应用KNN(K=1)、DT和PNN分类算法进行故障诊断仿真，结果记录如表4所示，可以看出，本文方法提取特征在不同分类算法中都获得了较高的故障诊断精度。

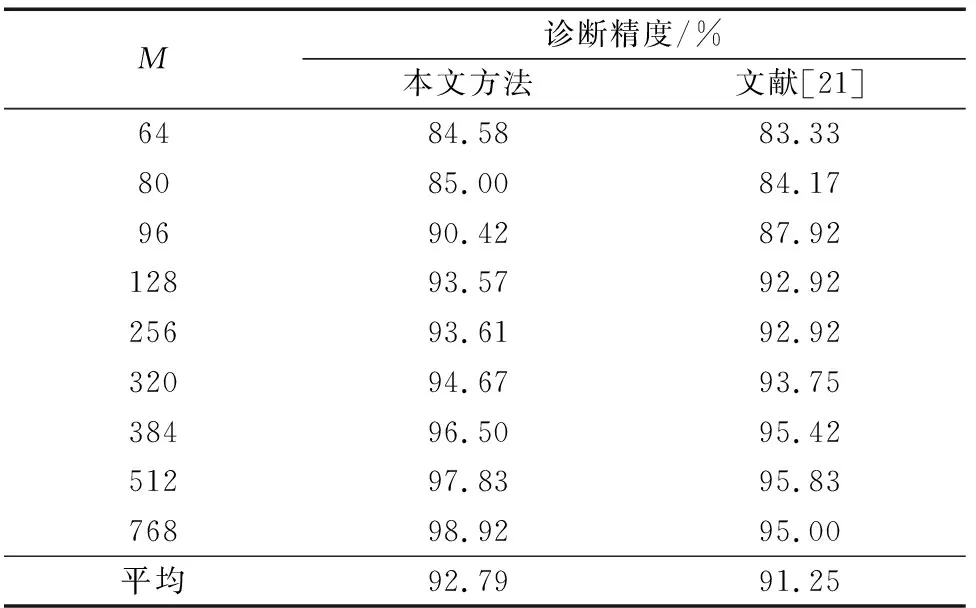
表3 不同特征提取方法的故障诊断精度Table 3 Fault diagnosis accuracy of different feature extraction methods

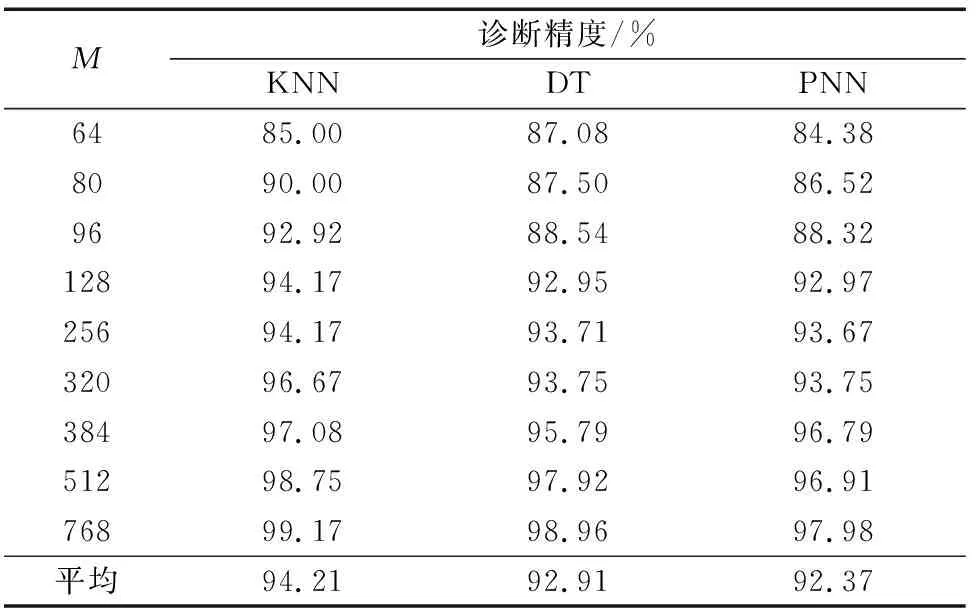
表4 不同分类算法故障诊断精度Table 4 Fault diagnosis accuracy of different algorithms

4 结论

针对滚动轴承在线监测和故障诊断应用，提出一种基于压缩感知和小波信息熵的滚动轴承振动特征提取方法。基于不同测量矩阵构造方法、不同压缩率和不同分类算法，在标准实验数据上完成了特征提取和故障诊断实验。结果表明所提方法能够在较高的数据压缩率条件下，保持较高的故障诊断精度。

(1)提出一种基于压缩感知和小波信息熵的滚动轴承振动特征提取方法。其主要思想是针对在线监测和故障诊断实际需求，对压缩后的监测信号直接求取其故障诊断特征。

(2)滚动轴承故障诊断仿真分析表明，在测量矩阵的行向量选取上，选择前M′行向量构造顺序Parthadmard矩阵作为测量矩阵，相比其他构造方法具有更高的诊断精度。

(3)仿真结果表明，传统采样方法中振动信号分析的小波包分解最佳层数方法，在压缩后的信号处理中仍然适用。