基于MIMO的多无人机辅助移动边缘计算系统时延优化设计

邹昳琨 王 钢 王金龙 刘浩洋

(哈尔滨工业大学电子与信息工程学院 哈尔滨 150001)

1 引言

近年来无人机(Unmanned Aerial Vehicle, UAV)凭借其强大的机动性、较高的灵活性以及较低的采购和维护成本逐渐成为商业应用的实用选择[1,2]。其中，单个或多个无人机经常作为通信中继器或空中基站用于紧急情况下的网络供应、公共安全通信和辅助蜂窝网络通信[3–5]。固定部署的基础设施无法满足资源需求过载和高动态性的要求，无人机通过合理的轨迹设计能够有效缩减通信距离、规避障碍物，提升通信质量、减少基础设施成本[6]。同时在移动边缘计算(Mobile Edge Computing, MEC)网络中，通过将计算任务卸载给物联网设备附近部署的计算资源(即在无线接入点或基站部署移动边缘计算服务器)能够有效地减少延迟并节省物联网设备上的计算资源[7,8]。

目前，涉及无人机辅助蜂窝网络的移动边缘计算延迟的优化研究包括：文献[9]通过优化卸载率、用户调度和无人机轨迹，最小化用户间最大延迟总和。文献[10]研究了UAV-MEC系统中的联合任务卸载与资源分配问题，其中UAV为无法连接基站的移动用户提供计算服务并连接到边缘云进行计算，旨在满足移动用户的计算和通信需求以及所有移动的总服务延迟的情况下最小化UAV的总能耗。文献[11]研究了一种支持UAV的边缘云系统，其中边缘云系统为每个地面终端实现了虚拟化网络功能，即移动克隆(Mobile Clone，MC)以帮助执行其卸载的任务，旨在联合优化资源配置和无人机在3维空间中的轨迹，以最小化无人机的整体能耗。文献[12]提出了利用UAV作为计算节点和中继节点来改善UAV-MEC网络中的平均用户时延，并以最小化所有UE的平均时延为目标来描述UAV-MEC问题。值得注意的是，UAV作为中继可以将用户数据传输给远端的宏基站进行处理。

上述文献中地面用户与无人机均配备单天线，大多采用时分多址方案在每一个时隙内服务一个用户。单输入单输出不仅带来了调度问题，同时限制了系统容量。在无人机通信中，无人机的收发消耗能量远远小于飞行消耗能量，这意味着单输入单输出严重限制了通信效率，减小了通信能量的利用率。同时研究者为提升网络指标，UAV需要借助外部资源加速UAV-MEC系统的计算过程，如作为中继将用户上传数据传输给宏基站或者边缘云。但现实情况中，系统数据的传输时间相较于计算时间可能更大，宏基站或者边缘云对于无人机的距离相对较远，会产生较大延迟，同时消耗更多能量。同时，无人机群在数量以及覆盖范围上的优势，决定了无人机群在MEC系统中拥有强大优势。一方面，机群中多个无人机的计算资源总和有一定规模，无人机间的相互协作能够有效利用无人机群的闲置资源；另一方面，机群中无人机的距离相对较近，且为视距(Line Of Sight, LOS)信道，能够有效缩短数据传输时间，增强通信传输质量，降低无人机能耗。在本文中，我们提出了一种基于多输入多输出(Multiple Input Multiple Output,MIMO)的多用户多无人机移动边缘计算系统。主要贡献概述如下：

(1)构建地面用户-辅助无人机-临近无人机的两层通信架构，减少数据传输时间，提高通信传输质量。

(2)用户信道模型采用莱斯信道，辅助无人机通过迫零检测解码用户信息，并采用迫零(Zero-Forcing, ZF)波束赋形和块对角化方案消除临近无人机干扰。

(3)基于两层通信结构，提出最小化系统最大总时延问题，包括地面用户到临近无人机的多条链路。

(4)考虑一个联合无人机轨迹、地面用户卸载比、辅助无人机卸载比和辅助无人机数据分发比的迭代优化算法，并采用连续凸优化技术和块坐标下降技术来解决其中的非凸问题。

本文的其余部分安排如下。第2节展示了系统模型。3.1节和3.2节基于MIMO的联合无人机轨迹、地面用户卸载比、辅助无人机卸载比和辅助无人机数据分发比的优化算法被提出。3.3节分析了算法的收敛性。第4节详细说明了仿真分析。第5节对全文进行了总结。

注意：对于一个矩阵A,AH代表其共轭转置。Id表示d×d单位阵。E(·)代表统计期望。Ca×b代表a×b复数矩阵的空间。N(a,b)表示均值a和方差b的高斯分布。‖A‖F表示矩阵A的F范数。

2 系统模型

如图1所示，本文考虑了无人机辅助多地面用户的边缘计算过程。K个装备单天线的用户上传数据后，装配有M个天线的辅助无人机保留一部分计算任务的同时向附近J个资源闲置的装配多天线的无人机传输剩余任务。注意：若将一个辅助无人机与其服务的多个地面用户组成一个单元，那么临近无人机实际上是周边相邻单元的辅助无人机。该系统设计能够扩展成为地面用户群和空中无人机群的数据交互过程。地面用户采用单天线设计有两点考虑：(1)本文旨在讨论双层通信架构对边缘计算系统性能提升的可行性。(2)在物联网地面传感器网络的边缘计算等场景中同样存在单天线场景。为消除接收端天线间的干扰，该系统在辅助无人机和临近无人机间采用了块对角化方法和迫零波束赋形技术，同时在地面用户和辅助无人机间的辅助无人机接收端采用迫零检测。假设无人机在用户周期T>0内使用相同带宽的不同频带进行通信。根据MIMO理论，系统的容量和min(K,M)成正比，因此为了方便讨论，本文假设K ≤M=J。

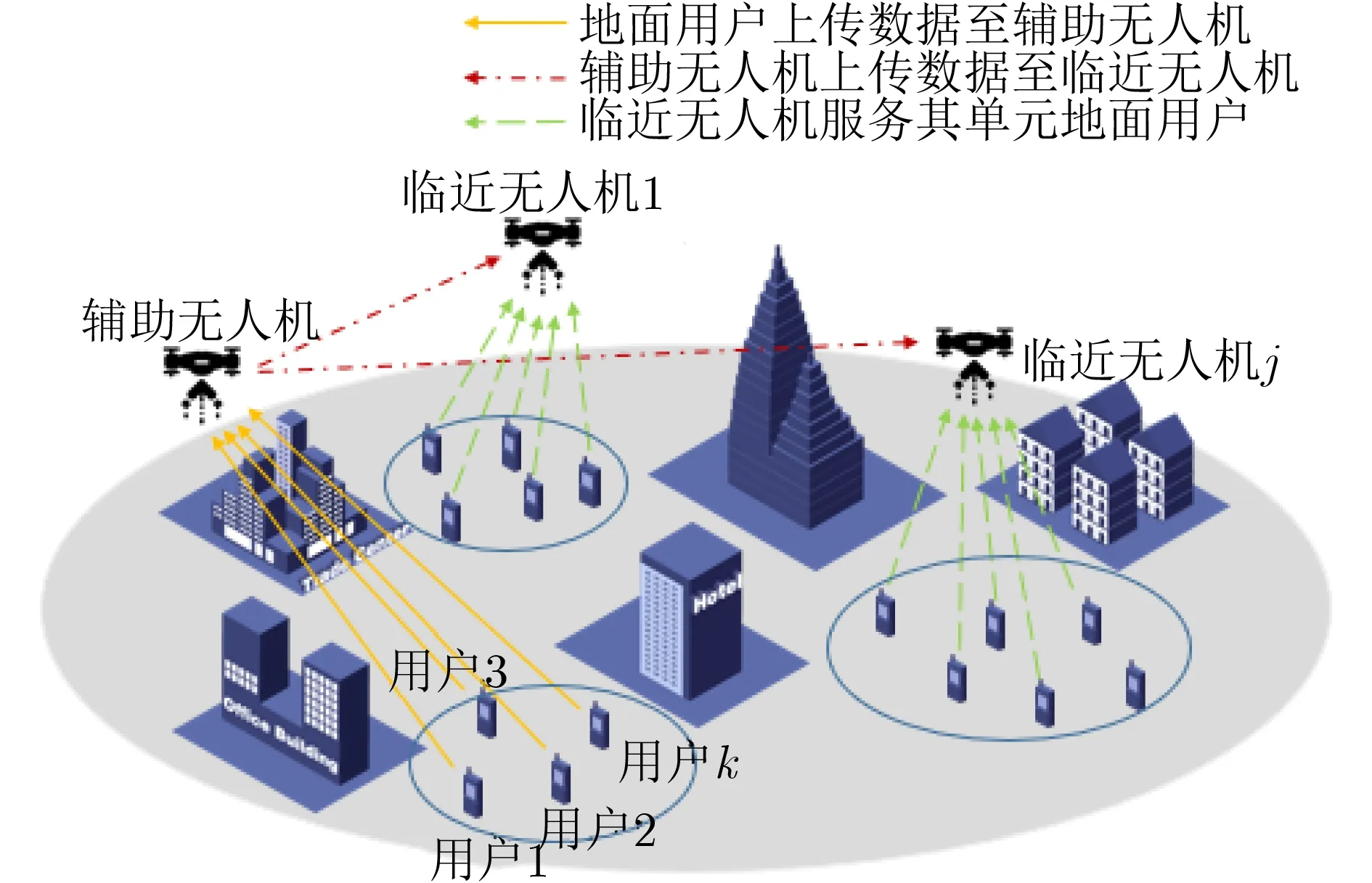
图1 系统模型

2.1 无人机轨迹模型

本文采用3D笛卡儿坐标系，其中第k个用户的位置可以表示为uk=[xk,yk,zk]T∈R3×1。为了便于分析，飞行过程被离散化。假设无人机的最大飞行速度为Vmax，周期T分为N个时隙。离散化后辅助无人机和临近无人机j在时刻n的位置为q(n)=[x(n),y(n),z(n)]T∈R3×1和qj(n)=[xj(n),yj(n),zj(n)]T∈R3×1。在周期T内无人机位置应满足以下条件

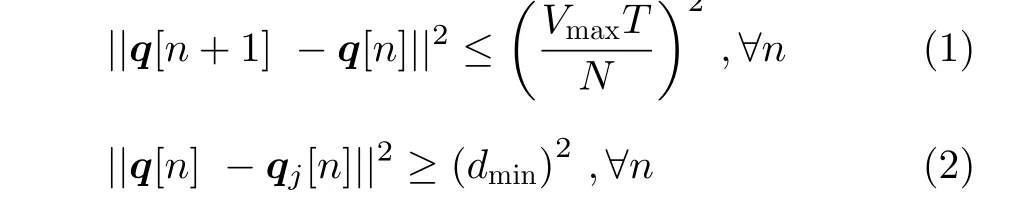
其中，dmin表示辅助无人机与临近无人机间的最小安全距离。同时，假定辅助无人机和临近无人机的飞行高度均固定。

2.2 通信模型

2.3 计算模型

其中，MUAV表示无人机质量(包括其有效载荷)。周期T内，临近无人机j的本地计算消耗能量为

为简化收发器的设计，我们考虑最常见的波束赋形方案-迫零过程。辅助无人机轨迹、用户卸载比、辅助无人机卸载比和临近无人机任务分配系数分别为Q={q[n],∀n}，L={lk[n],∀k,n}，M={m1[n],∀k,n}，b={bj[n],∀j,n}。假设地面用户和临近无人机的位置已知的条件下，本文的目标是通过联合优化UAV轨迹、用户卸载比、辅助无人机卸载比和临近无人机任务分配系数最小化整个周期T内系统最大总时延。优化问题表示为

式(22b)，式(22c)分别对应无人机最大飞行速度约束和飞行轨迹约束。式(22d)–式(22g)表示用户卸载比、辅助无人机卸载比和临近无人机任务分配比约束。式(22h)–式(22k)分别表示临近无人机计算约束、地面用户、辅助无人机和临近无人机能量约束。问题式(22)由非凸的目标函数构成，因此很难被直接解决。

3 联合优化算法

由于目标函数、轨迹以及能量约束对于辅助无人机轨迹仍是非凸的，因此，优化问题式(25)无法用现有的凸优化方法解决。在这一节中我们将通过采用连续凸优化技术解决优化问题式(25)，并利用块坐标下降法为问题式(25)提出一种有效的迭代算法。

3.1 用户卸载比、辅助无人机卸载比和临近无人机任务分配比优化

对于给定的变量集合{Q,M1,b}，简化问题式(25)为优化问题式(26)

3.2 无人机轨迹优化

对于给定的变量集合{L,M1,b}，简化问题式(25)为优化问题式(29)为

优化问题式(34)是一个凸优化问题，它可以用标准的凸优化求解器求解。注意，优化问题式(34)求得的最优目标值是优化问题式(29)最优目标值的上界。

3.3 整体算法与收敛性

上述收敛性分析可知每次迭代后整体的目标值是不增的。同时，因为问题式(25)的目标函数min(·)的目标值是有下界的，因此算法1保证收敛。同时，本文简化了现有的初始化方案[15]使得单无人机通过确定地面用户几何中心，从而确定无人机飞行初始轨迹，以覆盖每个时隙内所有服务用户。

表1 针对问题式(25)的优化算法

4 数值分析

表2 部分仿真参数列表

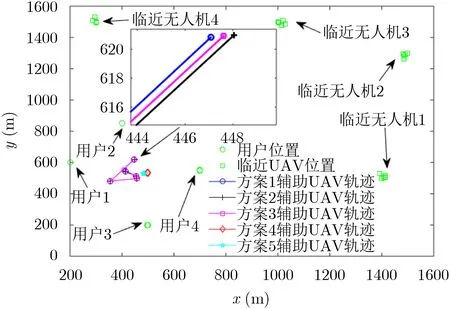
图2 5种方案的辅助无人机轨迹对比图

图2中相较于方案1，方案2的轨迹小幅偏向于临近无人机群方向。由于临近无人机计算频率的增加，辅助无人机在不对用户信道造成较大影响的情况下通过缩短与邻近无人机的距离，以便将很多数据传输给临近无人机进行计算。相较于方案2，方案3的轨迹偏向于用户。这是因为随着数据量的激增，用户信道状态成为制约数据传输的重要因素，缩短系统延迟的关键在于改善用户信道让更多的数据被卸载，无人机通过靠近用户缩短传输距离，从而改善信道。方案4和方案5也印证了这一观点。对比方案2和方案4以及方案3和方案5，均通过采取视距信道取代莱斯信道初步改善用户信道状态后，辅助无人机能够靠近临近无人机群方向，减小与机群的通信距离，提高通信传输速率，从而上传更多数据协同处理。

表3中相较于方案1，方案2随着临近无人机计算频率的增加，辅助无人机向临近无人机群靠近，以求将更多数据传输给临近无人机帮助计算，从表3可以看出用户卸载比和辅助无人机卸载比都有了一定提升，临近无人机获得更多计算数据量，并缩短了延迟。表4的方案1和方案2佐证了该结论。相较于方案2，方案3中辅助无人机和临近无人机获得的数据比重明显增加，说明随着数据量的增加，用户越来越不能满足计算的要求，必须将更多的数据上传给无人机辅助计算。方案4和方案5同样印证了这一点。对比方案2和方案4以及方案3和方案5，用户信道的改善显著增加了辅助无人机和临近无人机的计算数据量(在表4中计算数据的增加也体现在所有临近无人机上)，从而大幅提升辅助计算效率，减小系统总延迟。表4中数据的分配量与辅助无人机–临近无人机的距离呈强相关，并且随着临近无人机计算数据的增加，这种分配关系将得到进一步的加强。表4对比方案2和方案3、方案4和方案5，只有临近无人机4的计算数据占比呈上升趋势，这说明当数据总量激增时，系统会优先将计算任务分发给最近的临近无人机，这也印证了数据分配量与距离的强相关。

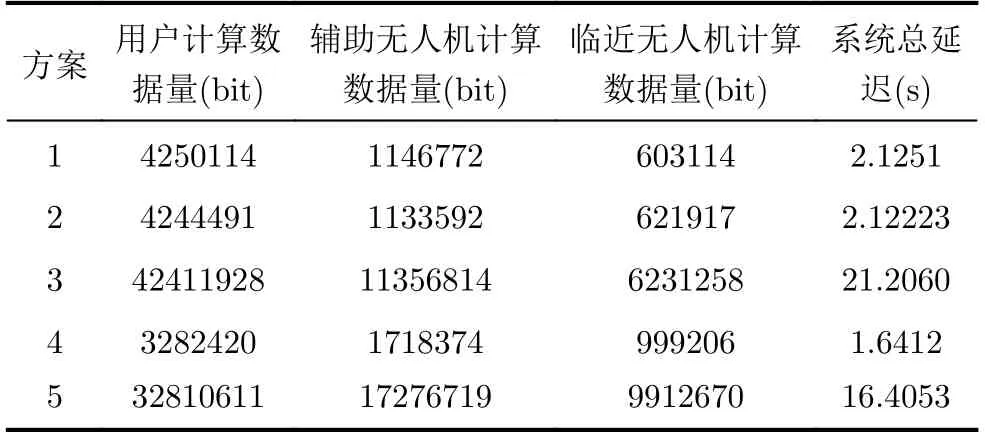
表3 5种方案的用户、辅助无人机、临近无人机计算数据量和系统总延迟对比

表4 5种方案的各临近无人机计算量对比(时刻n=1)

为了更好地说明临近无人机计算频率与系统总时延的关系，6种方法的用户信道均采用视距信道、辅助无人机计算频率4 GHz和数据总量3×105bit的条件：(1)本文算法；(2)辅助无人机悬停在用户几何中心上空；(3)辅助无人机采用初始化轨迹；(4)等卸载比等分配比方法(相等L,m1和b)；(5)无临近无人机方法；(6)无辅助无人机和临近无人机方法。图3表明本文方法的优势，同时说明了临近无人机计算频率的增加对系统总时延减小的趋势。方法1、方法2和方法3说明了无人机在每个时隙找寻最优点比大范围的规则轨迹更具优势，而MIMO技术会放大这种优势；方法4说明各层卸载比对缩减系统延迟起到决定性作用，卸载比的影响甚至超越辅助无人机轨迹优化的影响；方法5和方法6表明无人机对于边缘计算系统的性能带来显著提升。上述分析可以看出在无人机移动边缘系统中，辅助无人机对系统的影响最大，其次是卸载比和分配比，但是无人机轨迹的优化和临近无人机群的辅助也具有较大影响和更深的潜力。图4中方法2在大约40次迭代处收敛，方法4则在20次迭代处收敛。

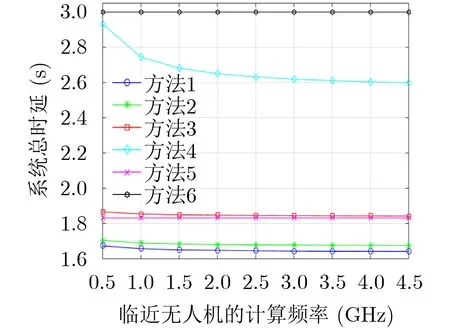
图3 不同方法下临近无人机计算频率与系统总时延关系的对比图(周期T=30s，N=5)

图4 方案2和方案4的收敛对比图

5 结束语

本文针对移动边缘计算系统计算资源不足的问题，构建了双层多无人机移动边缘计算系统。该系统通过MIMO技术和多临近无人机辅助计算，增强系统容量，减少系统总时延。其中，通过联合优化用户卸载比、辅助无人机卸载比、临近无人机任务分发比和辅助无人机轨迹从而最小化系统最大总时延。针对系统产生的非凸问题，我们采用连续凸优化技术和块坐标下降法将其转化为凸问题并求解。仿真部分针对不同因素对系统总时延的影响进行了讨论，并验证了本文算法的有效性和收敛性。