一种集中式四自由度磁轴承振动抑制方法

张灵修，张广明，欧阳慧珉

(南京工业大学 电气工程与控制科学学院，南京 211816)

0 引 言

与传统机械轴承相比，磁轴承具有无机械摩擦、使用寿命长以及动力损失小等优势，在飞轮储能、超高速金属切削加工和高速透平机械等领域有着极为广泛的应用前景[1]。

转子的质量不平衡会在旋转过程中产生大小与转速平方成正比、方向随时间变化的同频扰动，是系统中主要的扰动来源[2]。由于直接对转子的不平衡参数进行准确测量存在较大难度，在运行中对同频扰动观测和抑制更为可行。对此，国内外学者开展了广泛的研究，主要包括：基于变步长迭代搜寻的方法[3]、基于同步旋转坐标系的方法[4]、基于干扰观测器的扰动补偿方法[5]以及基于扩张状态观测器的扰动估计和补偿方法[6]。在现有研究成果中，虽然能够在低转速下对同频扰动抑制取得不错的效果，但大多采用了分散控制策略，并采用线性化的方式对电磁铁模型进行处理。由于线性化仅在工作点附近很小范围内准确，因而在定转子接触、磁通饱和等极限情况下，采用线性化电磁铁模型设计的控制器存在难以达到预期控制性能的问题。另一方面，由于将自由度之间的耦合作用内模化并纳入控制系统稳定性的考虑范围，在高转速工况下H∞鲁棒控制[7]等集中控制策略比分散控制策略具有更好的适用性，但存在计算资源需求量大和难以实现宽转速范围抗扰等问题。

针对上述问题，本文研究了以电磁力作为控制量的可行性，将扩张状态观测器与集中控制策略相结合，提出了一种以电磁力为控制量的四自由度状态反馈扰动抑制算法，并进行了仿真实验。本文的结构如下：

(1) 建立考虑转子陀螺效应变化和轴承动、静不平衡作用力的磁轴承动力学模型。

(2) 以电磁力为控制量，从系统总能量角度出发设计了考虑耦合作用模型和外部扰动补偿的集中式四自由度状态反馈控制器，并证明了其稳定性。

(3) 设计线性扩张状态观测器(LESO)对同频扰动进行观测，并通过所设计的控制器进行抑制。

(4) 利用Matlab进行实验仿真，对所提出的控制算法进行验证。

1 磁轴承-转子动模型

忽略轴向自由度和径向自由度之间的耦合，并假设转子工作在刚性模态下[8]，建立如图1所示的坐标系统。

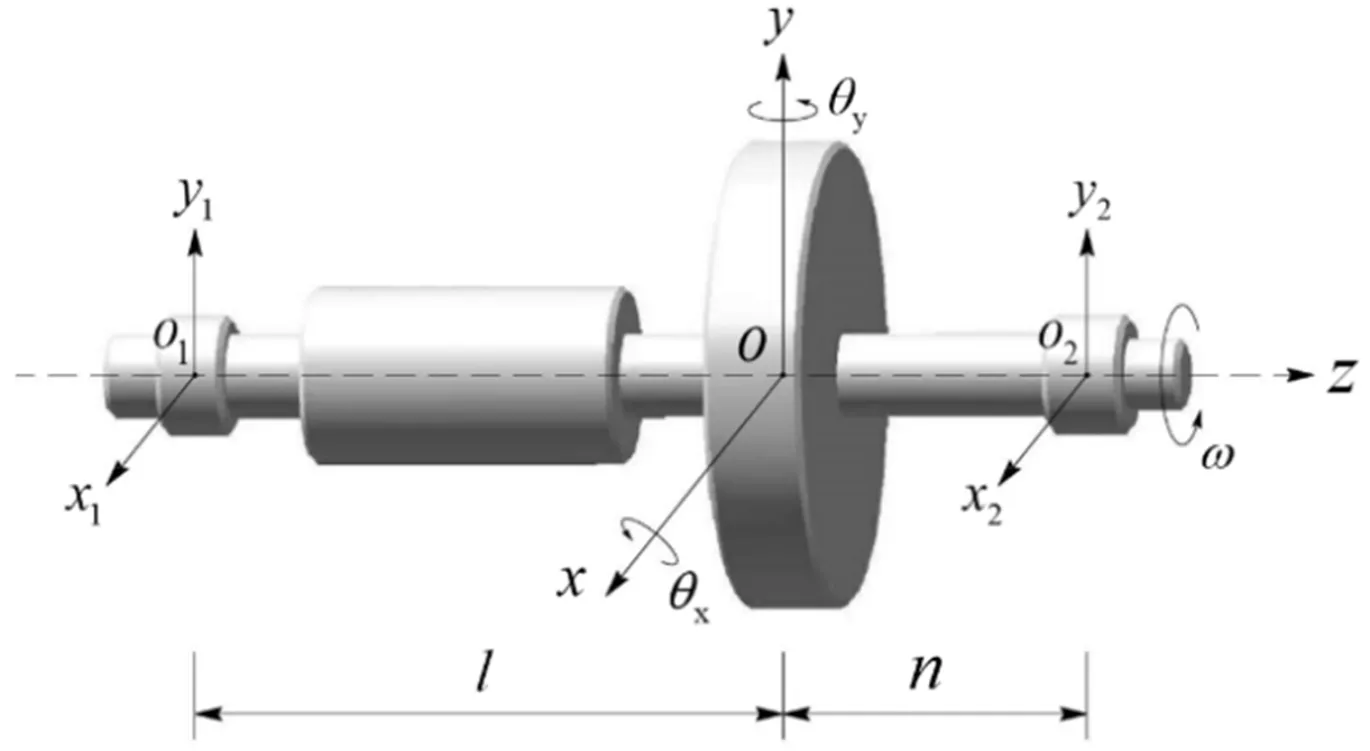
图1 转子空间运动示意图

其中o-xy为质心坐标系，o1-x1y1为左侧的轴承坐标系，o2-x2y2为右侧的轴承坐标系；l和n分别为左侧和右侧轴承距离质心的距离；θx和θy分别为转子在x轴和y轴方向转动的角度。

根据牛顿第二定律，当转子质心偏离平衡位置xg和yg时，有

(1)

式中,m为转子的质量，g为重力加速度，ω为转子的转速；转子在x轴和y轴方向上的转动惯量分别为Jx和Jy；左侧和右侧磁轴承作用在转子上的控制力分别为fLx、fLy、fRx和fRy；不平衡力和力矩分别为fex、fey、Tεx和Tεy。

式(1)的矩阵形式

(2)

其中

当转子旋转时，不平衡力和力矩在质心坐标下可表示为[2]

(3)

式中,δ为转子实际的质量中心和几何中心之间的偏差；ε为实际的惯性轴与几何轴之间的夹角；φ为不平衡力和力矩的初始相位。

记xL和yL分别为x1和y1方向上的位移距离，xR和yR分别为x2和y2方向上的位移距离。根据轴承坐标与质心坐标之间的近似变换关系，可得

(4)

定义误差向量为

(5)

(6)

将式(5)和式(6)代入式(2)中，可得转子在轴承坐标系下的以偏差量表示的运动方程

(7)

进一步对式(7)进行移项和变换，可得

(8)

其中

(9)

为不平衡扰动产生的加速度向量。比较式(3)和式(9)，可得

(10)

2 控制器设计

2.1 四自由度状态反馈控制器

差动式电磁铁的数学模型可以表示为如下的非线性的形式

(11)

式中,x为轴承坐标下转子偏离平衡点的距离；i为差动控制电流；s0为平衡点处转子与电磁铁之间气隙的长度；i0为平衡点电流；k为与磁轴承及转子结构有关的综合性参数。

在式(11)所给出的电磁铁模型及约束条件下，不难验证i(t)可由f(t)和x(t)唯一地反向计算得到。因此以f(t)作为待设计控制量与以i(t)作为控制量并无本质区别[9]，但能在控制器设计中使用更为精确的电磁铁模型。

对式(7)进行等价变形，可得

(12)

构建如下的非负能量函数

(13)

其中Kp为正定矩阵。

对式(13)求导，可得

(14)

将式(12)代入式(14)，有

(15)

如果Funb是已知的，构造如下反馈控制器

(16)

式中,Kd为正定矩阵。

将式(16)代入式(15)，化简后可得

(17)

由于式(16)所给出的控制律是在Funb已知的假设下得到的，但对于实际转子往往难以得到δ和ε的准确数值，因而需要通过扰动观测器对Funb进行估计。

2.2 扰动观测和估计

为了估计Funb的各个分量，现在以其第一个分量为例说明本文所提出的扰动观测器的设计方法。

由式(8)得左侧x轴方向下的转子运动方程为

(18)

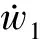
(19)

在式(19)的基础上将扰动力产生的加速度w1扩张为新的状态量x3，并通过构建扩张状态观测器(ESO)对系统状态量进行观测[10]。ESO的基本结构如图2所示

图2 扩张状态观测器结构图

其中u为观测器的输入信号，y为系统的输出信号，z1、z2和z3分别为状态量x1、x2和x3的观测值。设置观测器为如下线性形式

(20)

式中，b为输入增益，β01为位移反馈增益，β02为速度反馈增益，β03为扰动反馈增益。

当系统中的耦合关系模型比较准确且扰动有限时，为了降低观测器需要估计的总扰动范围，进而平滑输出曲线并降低对噪声的敏感[11]，可将u取为如下形式

(21)

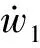
通过类似方法在其他坐标系方向分别设置上述状态观测器，可得

(22)

将式(22)代入式(10)，有

(23)

即得到了反馈控制器所需的Funb的观测值。

3 仿真验证

通过搭建磁轴承系统Matlab/Simulink模型，验证本文所述控制器对于同频扰动的抑制效果。磁轴承系统参数及给定的动、静不平衡参数如表1所示。

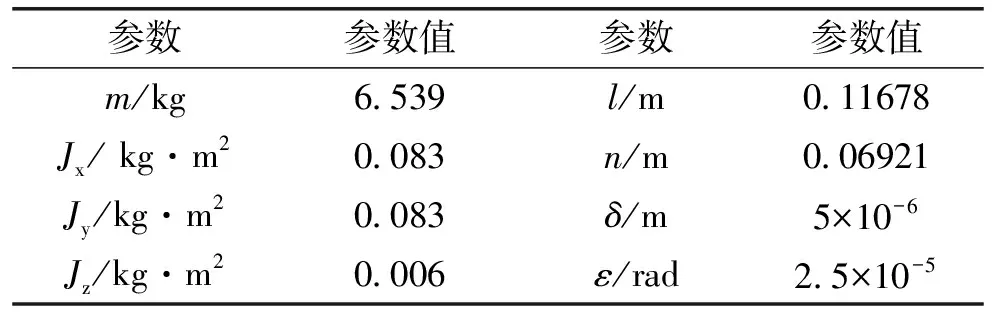
表1 系统参数

在进行对比的控制器中，两个控制器的Kp和Kd参数保持一致，各坐标系不同方向下的LESO参数通过带宽概念分别进行整定。根据控制器稳定条件，可将Kp和Kd取为如下形式

Kp=diag(kp1,kp2,kp3,kp4)

Kd=diag(kd1,kd2,kd3,kd4)

状态反馈控制器及LESO的参数如下表所示。

表2 控制器参数

转子转速变化曲线如图3所示。

图3 转速ω变化曲线

在0 s至1 s内转子转速不断上升，达到30000 r/min后保持匀速。

图4为左侧x轴处LESO对于不平衡扰动加速度w1的观测值与实际值的对比，图中虚线为扰动加速度的观测值，实线为扰动加速度的实际值。由图可见，观测器能够快速且准确地跟踪扰动信号。

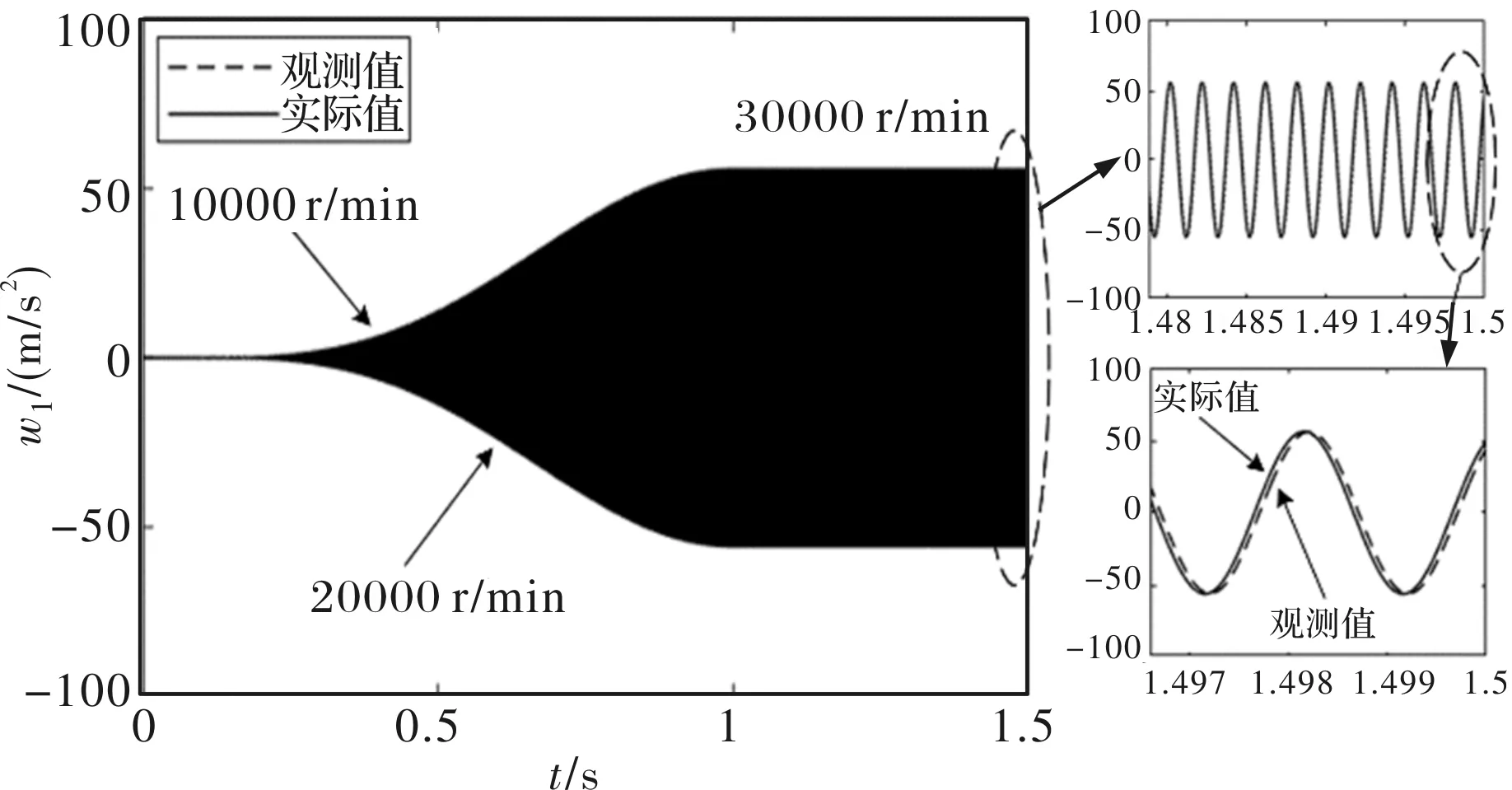
图4 左侧x轴处w1观测值与实际值的比较

图5为左、右轴承处转子的位移波动情况对比。图中实线为未采取扰动补偿措施的位移波动，虚线为扰动补偿后的位移波动。由图可见采取扰动补偿措施后，转子位移波动幅值在不同转速下均有明显下降。

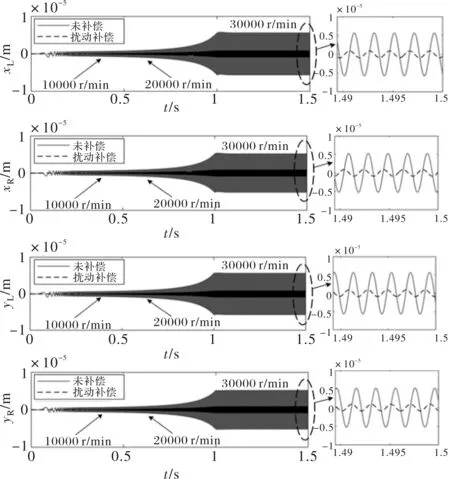
图5 左、右轴承处转子位移波动对比

为量化分析扰动补偿对于转子加速阶段和匀速阶段的扰动抑制效果，从图中取三个不同转速时转子的位移波动幅值情况进行定量分析，如表3、表4和表5所示。

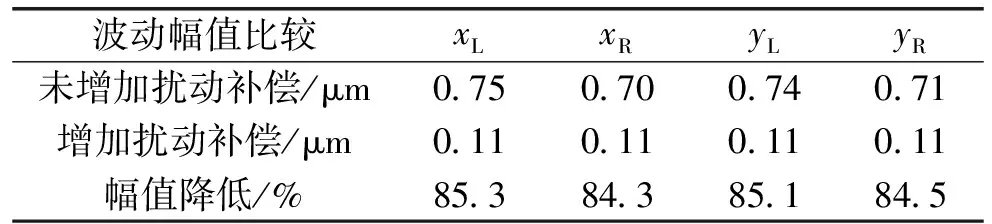
表3 干扰抑制特性比较(10000 r/min)

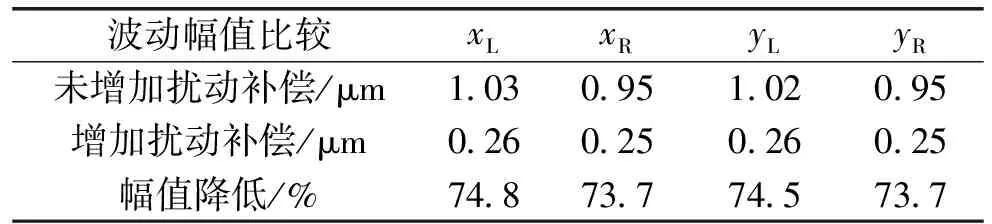
表4 干扰抑制特性比较(20000 r/min)

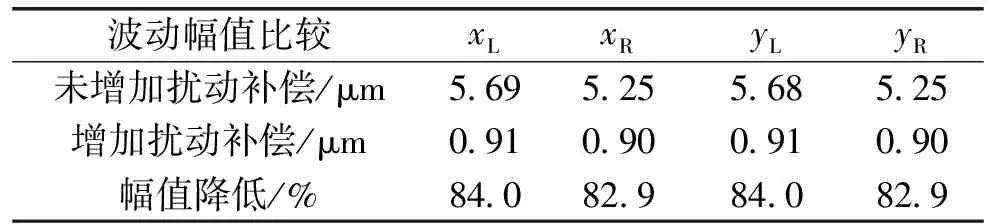
表5 干扰抑制特性比较(30000 r/min)

由表3和表5可以看出，在加速初始阶段以及匀速阶段位移波动幅值可降低80%以上；而在转速上加速度较快阶段，如表4所示，抑制效果依然能够维持在70%以上。

4 结 论

本文通过对磁轴承转子在运行中的空间运动状态进行建模和分析，从系统能量角度设计了集中式四自由度状态反馈控制器，并进行了稳定性分析；控制器以电磁力作为系统控制量，使其对于更为精确的非线性电磁铁模型具有更好的适用性；通过Matlab仿真，验证了集中式四自由度状态反馈控制算法的可行性和LESO对于同频扰动的观测及补偿效果，仿真结果表明本文所提出的组合控制器能够在较宽的转速范围内对转子同频扰动进行观测和主动抑制，转子运行精度提升显著。