基于模型预测电流补偿的电压稳定控制策略

杨鹏明，刘彦呈，张珍睿，郭昊昊，于春来

(大连海事大学 轮机工程学院，辽宁 大连 116026)

0 引 言

船舶综合电力推进系统作为船舶发展的新趋势，其动力通常采用直流供电逆变器-电机驱动系统。永磁同步电机(PMSM)因其结构简单、功率密度高、效率高、损耗小等优点[1]，被广泛作为推进电机使用。PMSM驱动系统在严格调速和恒负载转矩下具有负阻抗特性[2]，导致系统随着电机功率的增加而出现不稳定的现象，具体表现为逆变器直流环节电压振荡[3]。这种不稳定现象是由于LC滤波环节输出阻抗与逆变器-电机系统输入阻抗不匹配造成的。

虽然增大电容可以使系统稳定，但是大容量电容体积大，耐压低且寿命短，降低了系统的可靠性。据统计，60%的驱动电路故障都是由大容量电容引起的[4]。使用可靠性更高的弱电容逐渐成为新趋势，然而弱电容会进一步降低驱动系统的阻尼，引起直流环节电压振荡。常用的稳定方法可以分为无源阻尼技术和主动阻尼技术。无源阻尼技术是在LC滤波器的电感或电容上串联一个电阻[5]，从而减小了LC滤波环节输出阻抗。但是，这种方法不仅会导致额外的功率损失，还会产生更多的热量，造成系统过热，影响系统的使用寿命。主动阻尼技术是利用Middlebrook稳定判据等作为分析工具，从电机控制角度提出了一系列方法来提高直流供电逆变器-电机系统的输入阻抗。文献[6-7]采用基于参考电流的补偿策略(RCC)，通过提取直流环节电压的小信号并注入到q轴参考电流中，以修改系统输入阻抗，增加系统的阻尼，抑制直流环节电压的振荡。其中，文献[6]采用高通滤波器提取信号，文献[7]采用带通滤波器提取信号。然而，这些方法的电流环都采用PI控制器，在实际应用中，由于控制和采样延时问题[8]，PI控制器的带宽不能很大，导致快速性能差。模型预测控制(MPC)因其优异的控制性能而被作为电机控制领域的一个新研究热点，根据控制量的不同MPC可以分为模型预测电流控制(MPCC)和模型预测转矩控制(MPTC)。MPCC作为非线性控制器，通过代价函数直接控制逆变器的开关引脚，与电流滞环控制类似，MPCC的动态响应快[9]。

本文提出了一种基于模型预测电流补偿的(RCC+MPCC)稳定控制策略。通过高通滤波器提取直流环节电压的振荡小信号并注入到q轴参考电流中，然后使用电流预测模型预测出下一时刻的电流值，最后根据代价函数从基本电压矢量中选取最优电压矢量使预测电流值跟随参考电流值。使用快速性能更好的MPCC替换PI控制器，可以提高直流环节电压和电机转速的性能。仿真结果验证了该方法的有效性。

1 系统建模和振荡机理

1.1 系统稳定判据

图1为直流供电逆变器-永磁同步电机传动系统拓扑简图。这种拓扑结构可由等效戴维宁电路和等效控制框图表示，如图2所示。由图2(b)可以判断系统的闭环传递函数为

(1)

式中，Zo(s)、Zin(s)分别代表源侧输出阻抗和负载侧输入阻抗。

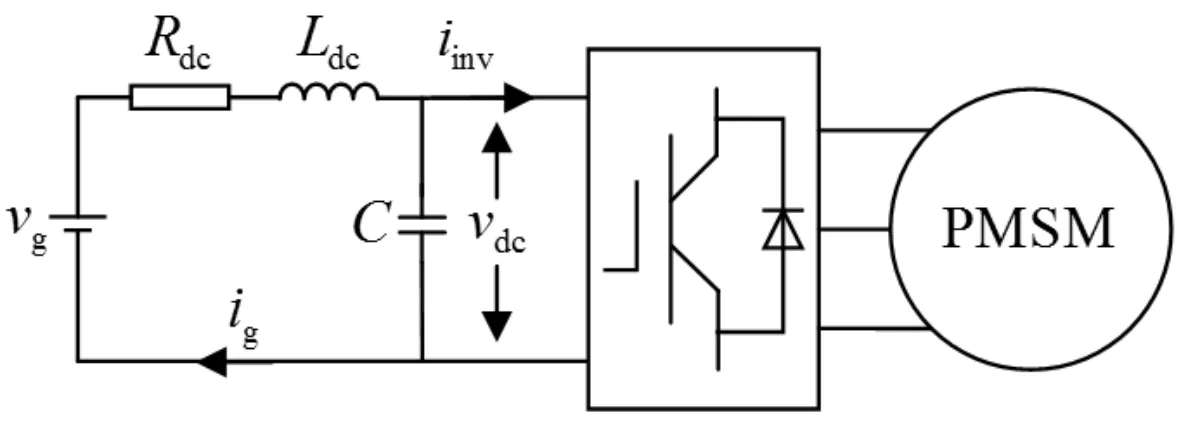
图1 系统拓扑简图

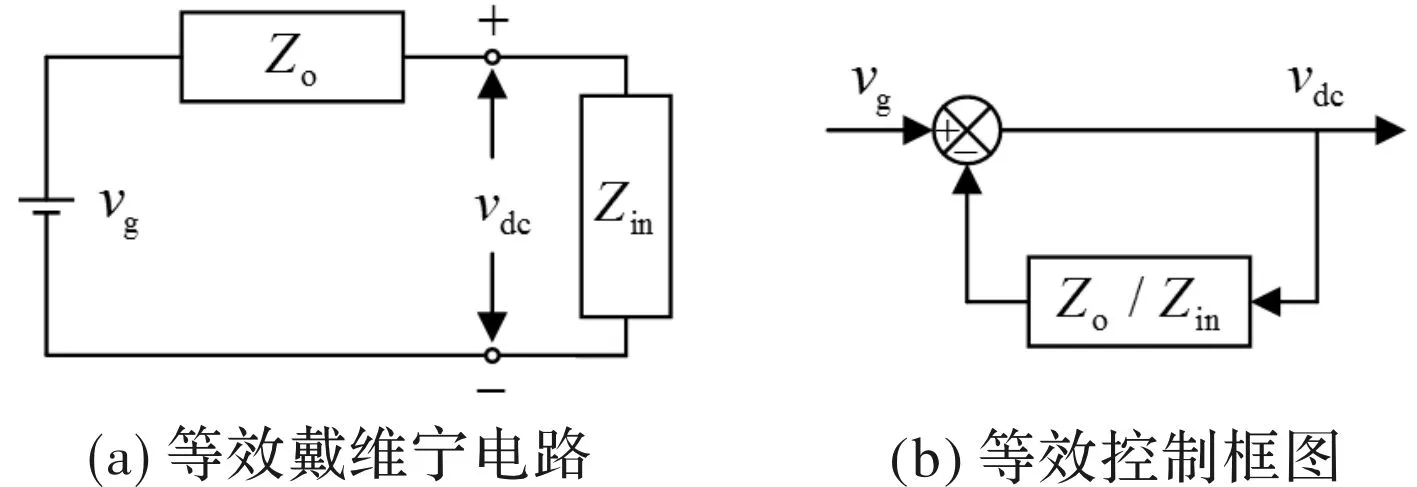
图2 系统等效图

由式(1)可知系统不稳定的根本原因是源侧输出阻抗Zo(s)与负载侧输入阻抗Zin(s)不匹配，即源侧与负载侧的阻抗比Zo(s)/Zin(s)不满足奈奎施特稳定判据。

1.2 LC滤波器的输出阻抗

由图1可知，根据基尔霍夫电压和电流定律可以得到源侧状态方程为

(2)

式中，vg、vdc分别代表电源电压和直流环节电压；ig、iinv分别代表电感电流和逆变器电流；Ldc、Rdc、C、t分别代表电感、线路电阻、电容和时间。

假设式(2)中的电源电压为常数，利用小信号的方法可以得到LC滤波器的小信号模型，为

(3)

式中，s为拉普拉斯算子；Δ代表相应参数的小信号。

根据式(3)，推导出LC滤波器的输出阻抗Zo(s)的小信号模型为

(4)

1.3 未补偿时负载侧的输入阻抗

永磁同步电机在dq坐标系下的电压方程和运动方程为

(5)

式中，vd、vq分别代表电机的d轴和q轴电压；id、iq分别代表电机的d轴和q轴电流；Ld、Lq、Rs、p、ψ、J、β分别代表电机dq相电感、相电阻、极对数、永磁体磁链、转动惯量和粘性摩擦系数；ωm代表机械角速度；TL代表负载转矩。

在dq坐标系下对逆变器进行建模时，可以用平均模型表示为[2]

(6)

式中，αd、αq分别代表逆变器占空比在dq坐标系下的d轴和q轴分量。

忽略逆变器的损耗，则逆变器的输入功率Pdc和电机消耗的功率PPMSM相等，因此逆变器输入功率和电机功率的关系表达式为

vdciinv=1.5(vdid+vqiq)

(7)

速度控制器和电流控制器的传递函数分别用Gs(s)和Gc(s)表示，因此q轴参考电流的表达式为

(8)

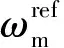
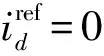
(9)

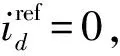
(10)

式中，Ωm、Iq分别代表机械角速度和q轴电流的稳态值。

逆变器的电压小信号表达式为

(11)

式中，Vd、Vq、Vdc分别代表电机d轴电压、q轴电压和直流环节电压的稳态值。

电机消耗功率与逆变器输入功率的小信号模型的表达式为

VdcΔIinv+IinvΔVdc=1.5(IqΔVq+VqΔIq)

(12)

式中，Iinv代表逆变器电流的稳态值。

q轴电流控制器的小信号表达式为

(13)

电机稳定运行时，电流环输出变化很小，dq轴参考电压的小信号为零[2]，即

(14)

联立式(10)、式(11)、式(13)、式(14)，可以得到ΔVdc和ΔIq的关系为

(15)

联立式(10)、式(12)、式(15)，并令β≈0，得到PMSM驱动系统的输入阻抗Zin(s)的小信号模型为

1.4 系统稳定性分析

目前，电机的高性能控制通常采用磁场定向控制，转速外环和电流内环使用PI控制器。根据PI控制器的传递函数和式(16)得到最终的输入阻抗Zin(s)以及式(4)的输出阻抗Zo(s)，在Bode图和奈奎施特图上表示出它们之间的关系，如图3所示。

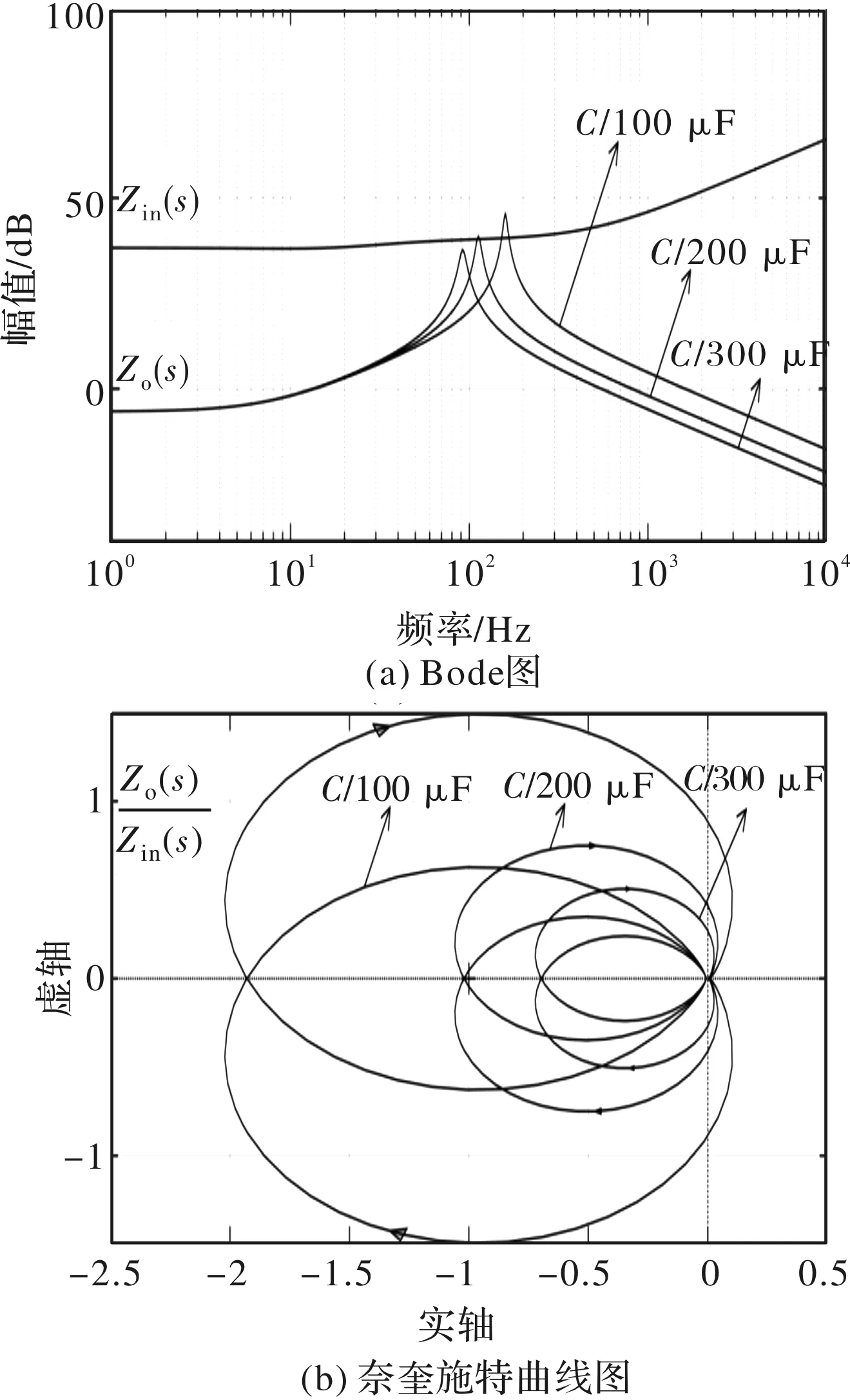
图3 不同电容下系统Bode图和奈奎斯特曲线

从图3(a)可以看出，直流供电逆变器-PMSM传动系统的电容的容值会影响源侧输出阻抗Zo(s)的谐振幅值。当电容减小时，源侧输出阻抗Zo(s)和负载侧输入阻抗Zin(s)存在重合部分，表明输出阻抗和输入阻抗不匹配，违反了MiddleBrook准则。从图3(b)也可以看出，当电容较小时，阻抗比的奈奎斯特曲线包围了点(-1,0)，系统是不稳定的。为了保证系统的稳定性，可以通过提高负载侧的输入阻抗来满足MiddleBrook准则。

1.5 基于参考电流的PI稳定控制策略

主动阻尼补偿技术的本质是利用电机的相电感吸收LC谐振引起的振荡能量，从而使系统稳定[10]。对于双闭环电机控制系统，基于参考电流补偿策略(RCC)的阻尼补偿信号注入点为转速外环的输出(q轴参考电流)，如图5所示。

采用高通滤波器和一个延时环节提取振荡信号并注入到q轴参考电流中，将延时环节等效成一个一阶惯性环节，则q轴电流控制器的小信号模型被改写为

(17)

式中，Kv、ωc为高通滤波器的增益系数和截止频率；Td为延迟环节的时间常数。

联立式(10)～式(12)、式(14)、式(17)得到补偿后的PMSM驱动系统的输入阻抗Zin(s)的小信号模型为

(18)

转速环和电流环的控制器采用PI控制器，则根据式(4)和式(18)在Bode图和奈奎施特图上表示出它们之间的关系，如图4所示。

从图4(a)可以看出，PI控制下补偿后的系统相比原系统提高了的输入阻抗，使其与输出阻抗不重合，满足了MiddleBrook准则，从图4(b)也可以看出补偿后系统的阻抗比的奈奎施特曲线不包围点(-1,0)，因此系统是稳定的。但是，由于控制和采样的延时问题，PI控制器的带宽不能很大，导致快速性能差。为此，提出了模型预测电流控制(MPCC)，以代替传统的PI控制。

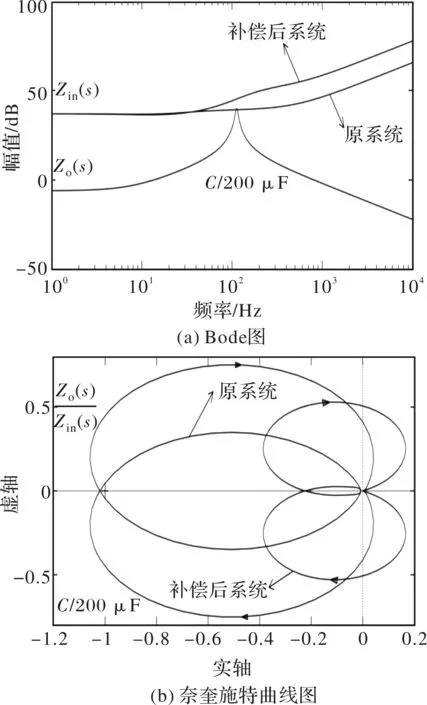
图4 补偿前和PI补偿后系统的Bode图和奈奎施特曲线

2 基于模型预测电流补偿的稳定控制策略

2.1 模型预测电流控制

MPCC的第一步是预测k+1时刻的电流。采用一阶前向差分法将式(5)中的电压方程离散化，用矩阵表示为

(19)

其中矩阵A和B分别为

(20)

式中，I代表单位矩阵；ωe(tk)代表电角速度在第k时刻的测量值；id(tk)、id(tk+1)、iq(tk)、iq(tk+1)分别代表d轴电流以及q轴电流在第k时刻的测量值和第k+1时刻的预测值；vd(tk)、vq(tk)代表两电平逆变器的八个基本电压矢量；Ts代表采样时间。

表1为αβ坐标系下两电平逆变器的基本电压矢量，其中包括六个非零矢量和两个零矢量。通过坐标变换将基本电压矢量变换到dq坐标系上。然后，根据dq坐标系下的基本电压矢量和电流预测方程(19)预测出八个k+1时刻的电流矢量。

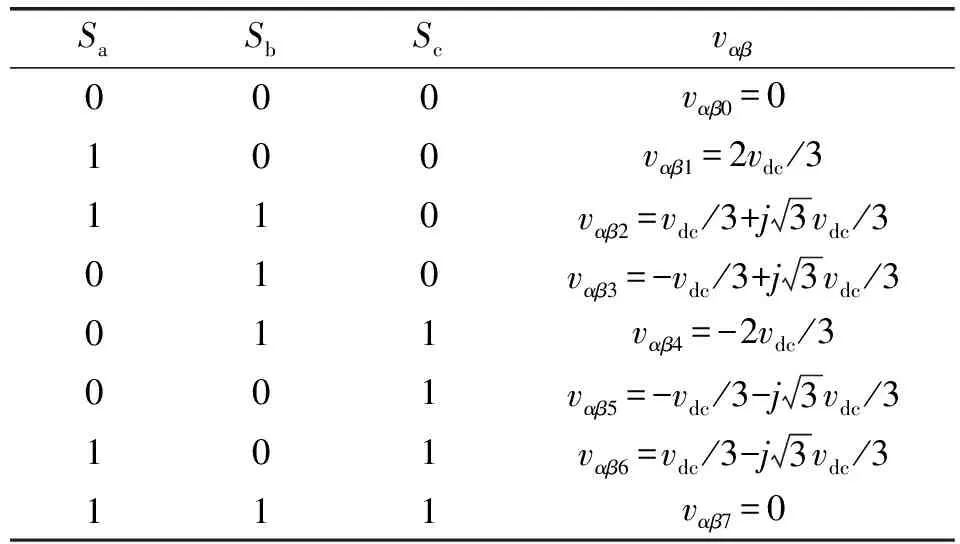
表1 αβ坐标系下两电平逆变器的基本电压矢量

MPCC的第二步是代价函数的评估，该算法决定了下一个采样时刻应用在逆变器上的开关状态Sa、Sb和Sc。为了评估八个预测电流矢量，定义代价函数为

(21)

根据式(21)算出八个基本电压矢量所对应的八个代价函数的值，从其中选出使代价函数最小的电压矢量输出，由于基本电压矢量与开关状态一一对应，所以MPCC不需要调制过程，而是直接改变逆变器的开关引脚，从而具有更快的动态响应。一步预测的MPCC的计算延时不可避免，通常采用二步预测的方法进行补偿[11]。

2.2 模型预测电流控制器的线性化

MPCC是一个非线性离散控制器，为了分析系统的稳定性，需要将控制器进行线性化[12]。将式(21)用矩阵的形式表示为

g=GTG

(22)

其中矩阵G为

(23)

将式(19)代入式(23)中得

(24)

其中矩阵F为

(25)

因此，矩阵GT可以表示为

GT=FT-Ts[vd(tk)vq(tk)]BT

(26)

联立式(22)、式(24)、式(26)将代价函数展开为

g=g1+g2+g3

(27)

式中参数分别为

定义电压矢量为

则式(27)对电压矢量的偏导为

(28)

令式(28)等于0，得到最优电压矢量为

(29)

为了验证所求的电压矢量为最小值，对式(28)二次求导为

(30)

由式(30)可知二阶偏导恒大于0，因此解为代价函数的最小值。

由于采样时间Ts很小，因此TsA≈0。联立式(25)、式(29)并进行相应简化得到

展开后得到MPCC的线性化模型为

(31)

由式(31)可知，当不考虑MPCC的非线性和离散性时，MPCC可以近似看成一个比例增益很大的比例控制器。

2.3 补偿后的负载侧输入阻抗

为了使系统稳定，采用高通滤波器和一个延时环节提取振荡信号并注入到q轴参考电流中，转速外环采用PI控制器，电流内环采用MPCC，控制框图如图5所示。

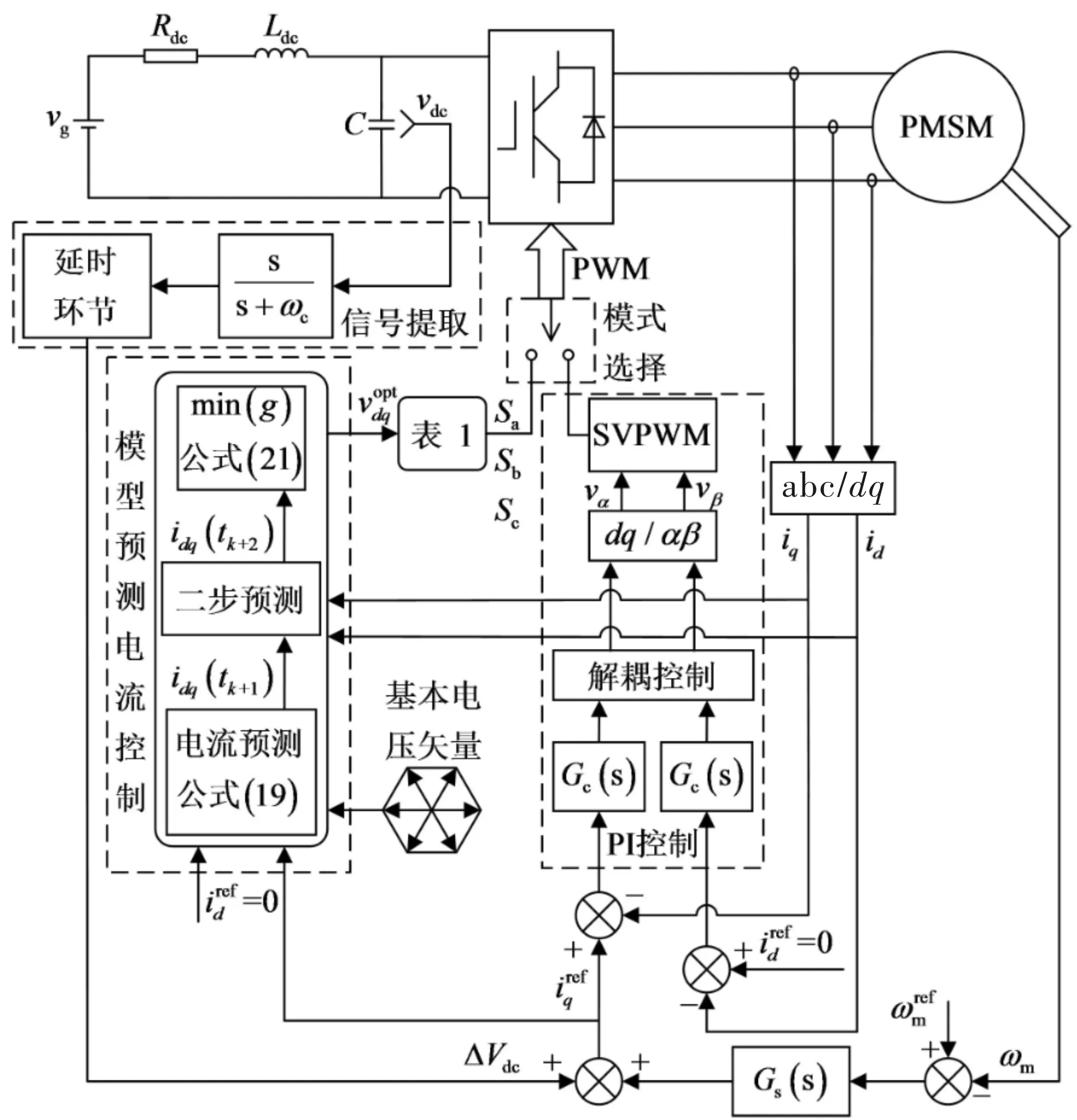
图5 系统控制框图

由式(31)可知，采用模型预测电流控制时，q轴参考电压为

(32)

联立式(17)和式(32)可知，采用MPCC时q轴参考电压的小信号为

(33)

转速环控制器采用PI控制器，则联立式(10)～式(12)、式(14)、式(33)得到MPCC控制下的PMSM驱动系统的输入阻抗Zin(s)的小信号模型为

(34)

其中，参数分别为

b0=2.25(Vq+VdcHv(s)Lq/Ts)Iqp2ψ2-1.5IinvVdcpψGs(s)Lq/Ts

2.4 补偿后系统的稳定性分析

转速环的控制器采用PI控制器，则根据式(4)和式(34)在Bode图和奈奎施特图上表示出它们之间的关系，如图6所示。

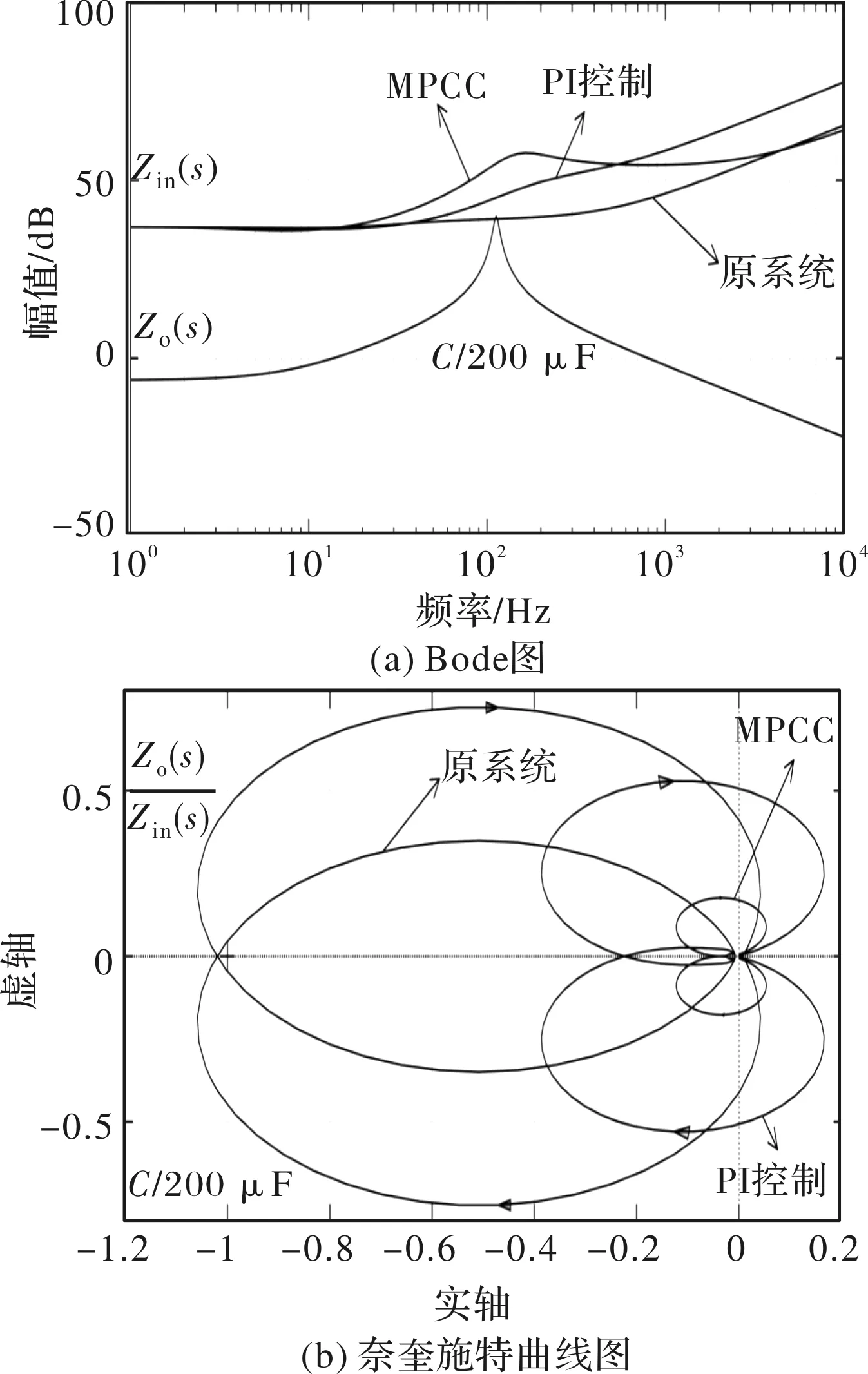
图6 补偿前和MPCC补偿后系统的Bode图和奈奎施特曲线

从图6(a)中可以看出，MPCC控制下补偿后的系统相比原系统提高了的输入阻抗，使其与输出阻抗不重合，满足了MiddleBrook准则，从图6(b)也可以看出补偿后系统的阻抗比的奈奎施特曲线不包围点(-1,0)，因此系统是稳定的。对比PI控制，MPCC能够提高更多的输入阻抗，即系统的稳定裕度更高，从图6(b)中也可以体现。

2.5 直流环节电压信号的提取

本文采用高通滤波器和延时环节来提取直流环节电压信号，因此需要设计高通滤波器的增益系数和截止频率，以及延时环节的延时时间。

高通滤波器需要提取直流环节电压信号中的振荡信号，因此高通滤波器的截止频率设置为系统的振荡频率。确定系统的振荡频率首先需要确定负载侧的功率和电流的关系，系统负载侧的功率和逆变器电流的关系为

(35)

将式(35)代入式(2)中得到整个系统的小信号状态方程为

(36)

式(36)的特征方程为

(37)

由于线路电阻Rdc的值较小，因此根据式(37)可以估算出系统的振荡频率ωr为

(38)

当电感Ldc=10 mH，电容C=200 μF时，根据式(38)估算出系统的振荡频率为112.5 Hz，因此，高通滤波器的截止频率ωc设置为112.5 Hz。

图7为不同增益系数下的MPCC补偿下输入阻抗和输出阻抗的Bode图。从图中可以看出，当增益系数较小时，Hv(s)≈0，注入的阻尼信号幅值太小，不能起到阻尼的作用，因此系统不稳定。当增益系数较大时，注入的阻尼信号幅值太大，相当于在电机起动时存在较大的扰动，不利于电机的稳定运行。因此，需要综合考虑增益系数Kv的选取，本文选取Kv=0.15。

图7 不同增益系数下的MPCC补偿效果

当ωc=112.5 Hz，Kv=0.15时，高通滤波器的Bode图如图8(a)所示。从图中可以看出，高通滤波器提取频率为112.5 Hz的振荡信号时，其相位会超前原振荡信号45°，从图8(b)中也可以看出，提取后的振荡信号的相位超前原振荡信号45°，因此仅采用高通滤波器提取振荡信号是无法起到阻尼效果。为了提高振荡信号的提取精确，必须将高通滤波器提取的振荡信号延迟45°，即1/4个振荡周期，因此，延时环节的延时时间设置为2.224 ms。从图8(c)可以看出，高通滤波器和延时环节提取的振荡信号的相位与原振荡信号基本相同。

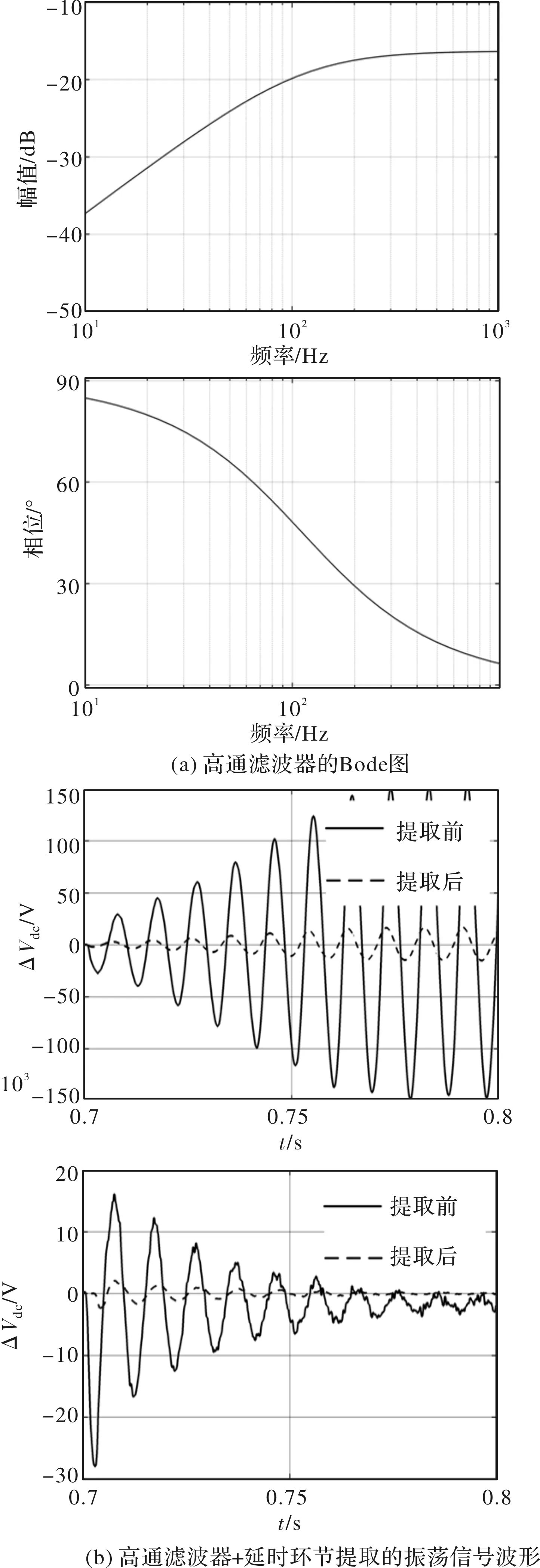
图8 系统振荡信号的提取波形

3 仿真验证

为了验证所提方法的有效性，本文根据图5在Matlab的Sumlink中搭建了仿真模型，并与基于参考电流的PI稳定控制的性能进行对比和分析。表贴式永磁同步电机型号为EML-10APB22。系统相关参数如表2和表3所示。

表2 LC滤波器参数

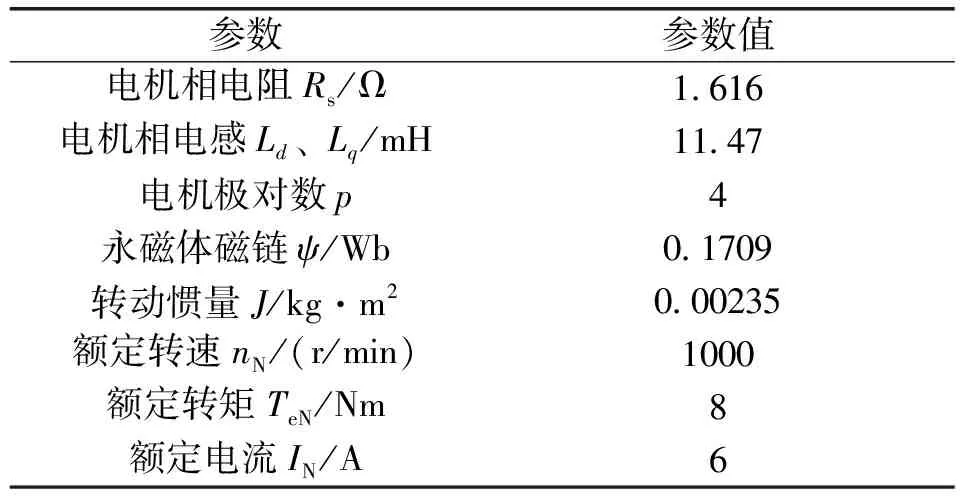
表3 表贴式永磁同步电机参数

3.1 RCC+MPCC的仿真验证

图9为C=300 μF且未补偿时轻载和重载下的直流环节电压和转速波形。从图中可以看出，无论轻载还是重载，系统都能依靠自身阻尼使系统稳定。因此当电容为300 μF时，系统总是稳定的，这与之前的分析完全一致。

图9 C=300 μF且未补偿时轻载和重载下的直流环节电压和转速波形

图10为C=200 μF时未补偿和RCC+MPCC补偿后直流环节电压和转速的波形图。从图中可以看出，当电机起动并到达额定转速时，由于负载转矩为零，电机功率小，未补偿系统的阻尼能够抑制直流环节电压的振荡。同时由于注入信号的影响，补偿后系统的直流环节电压和电机转速出现小幅度的波动。当0.4 s时突加8 Nm的负载转矩时，未补偿系统的阻尼已经不能抑制直流环节电压的振荡，导致系统不稳定。而RCC+MPCC补偿后的系统经过短暂的调节过程后，直流环节电压保持稳定。在q轴参考电流处注入的阻尼信号对电机而言是一种扰动，因此转速在起动和调节过程中会出现短时间的小幅波动。

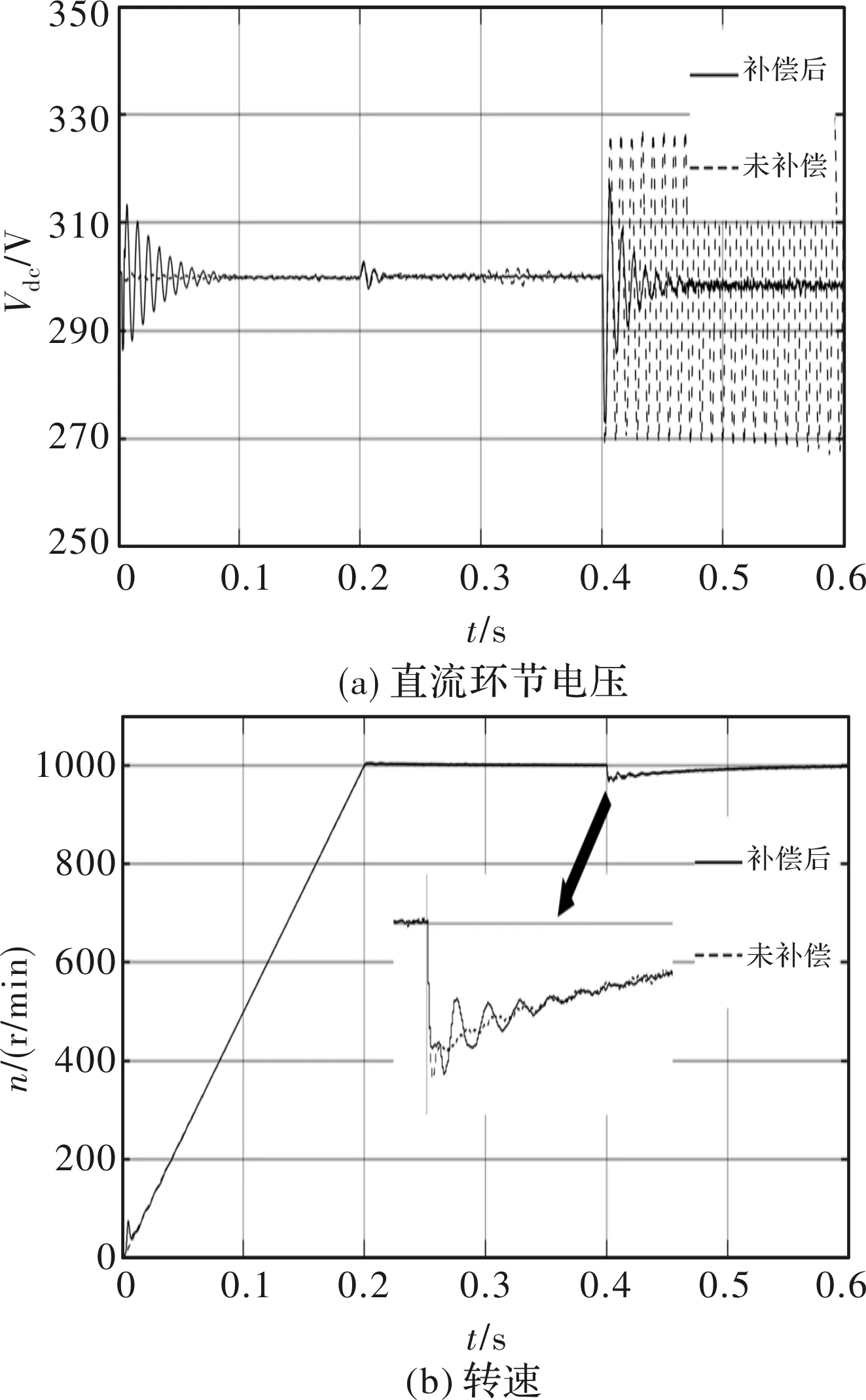
图10 C=200 μF时未补偿和RCC+MPCC补偿后直流环节电压和转速波形

3.2 RCC+PI和RCC+MPCC的仿真对比

图11为重载时PI和MPCC的对比仿真结果，转速外环的PI参数为Ksp=0.3和Ksi=3.5，PI电流内环的带宽为500 Hz。从图中可以看出，当电机起动并到达额定转速时，MPCC的直流环节电压的振荡幅值和转速的超调都要小于PI。0.5 s时突加8 Nm的负载转矩，MPCC的直流环节电压振荡幅值要小于PI且收敛速度更快，转速性能相差不大。表明重载时MPCC的直流环节电压和转速的性能要优于PI。

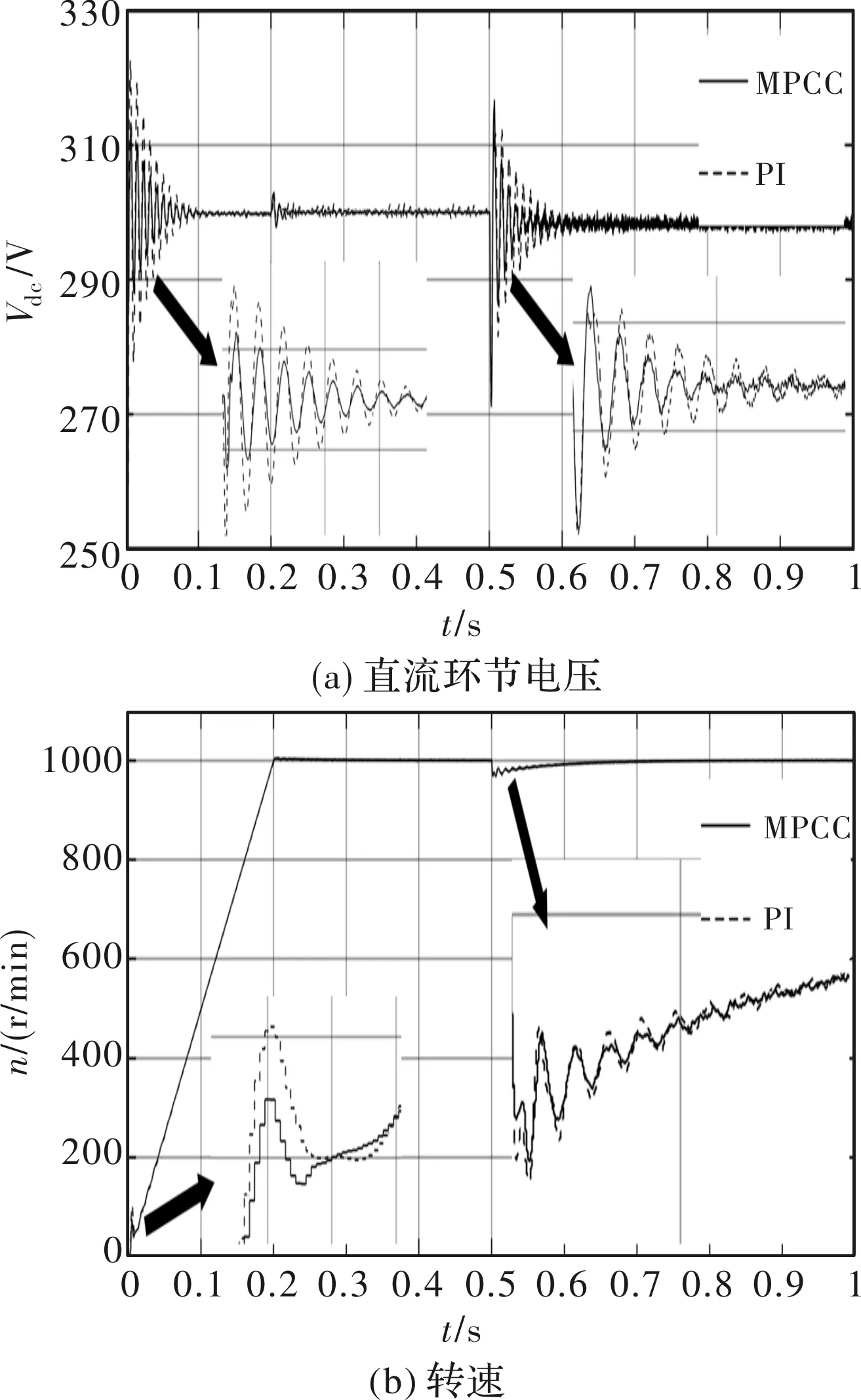
图11 重载下PI和MPCC的对比

图12为轻载时PI和MPCC的对比仿真结果，参数选取与图11一样。从图中可以看出，当电机起动并到达额定转速时，仿真结果和图11一样。0.5 s时突加2 Nm的负载转矩，MPCC的直流环节电压的动态性能与PI相差不大，但稳态精度比PI高，同时，MPCC的转速动态性能优于PI。表明轻载时MPCC的直流环节电压和转速的性能要优于PI。

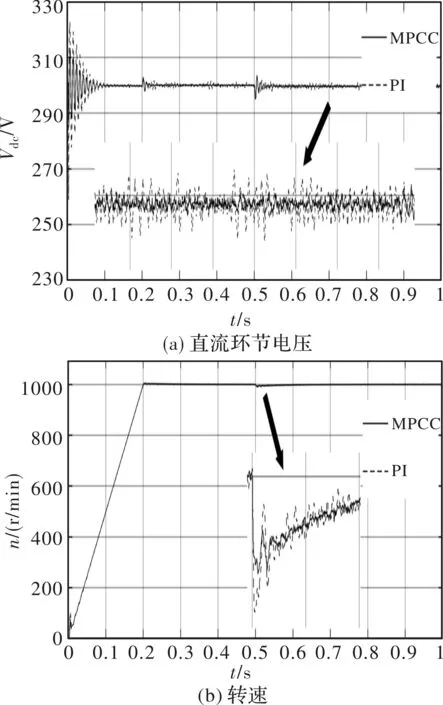
图12 轻载下PI和MPCC的对比

4 结 论

本文提出了一种基于模型预测电流补偿的稳定控制策略，通过在q轴参考电流注入直流环节电压小信号来抑制其振荡现象。同时，采用快速性更好的模型预测电流控制器替换PI控制器，提高了系统直流环节电压和电机转速的性能。仿真验证了本方法的有效性。