洛伦兹对称破缺框架下的广义克莱因-戈尔登谐振子*
王恩权 陈浩 杨毅 隆正文† Hassanabadi Hassan
1) (贵州大学物理学院,贵阳 550025)
1 引言
众所周知,应用于无自旋标量粒子的克莱因-戈尔登(Klein-Gordon,KG)谐振子[1,2]是受狄拉克谐振子[3,4]的启发而提出的,而狄拉克谐振子是在线性相互作用下描述自旋为1/2 粒子的物理对象.目前,相对论谐振子的推广,如KG 谐振子[5-10]、Kemmer 谐振子[11]、Duffin-Kemmer-Petiau 谐振子[12-14]以及狄拉克谐振子[15,16]的广义化是理论物理学家特别感兴趣的研究课题,尤其是在拓扑缺陷背景下的谐振子研究吸引了许多物理学家的兴趣.文献[8]在宇宙弦时空中通过一个新的动量算符来替代之前的动量算符实现了KG 谐振子的广义化,即作这样一个动量算符的替换:pµ →pµ+imωXµ.
此外,随着量子力学[17]和相对论的发展,由麦克斯韦电磁学衍生出来的规范理论已逐渐在物理学的各个分支中得到证实,如粒子物理学中弱电相互作用的统一解释了放射性衰变现象,基于希格斯机制,阐明了粒子物理学中的对称性和对称性自发破缺问题,建立了统一除引力之外的所有相互作用的标准模型(standard model,SM).然而,SM 面临着一些无法解释的物理现象,如暗物质和暗能量及引力相互作用等,因此,Kosteleck 和Samuel[18]在弦理论的基础上提出了具有洛伦兹对称破缺(Lorentz symmetry violation,LSV)的标准模型扩展理论(standard model extension,SME).后来,在考虑有效场论的情况下,具有量子效应的SME 得到了广泛应用.如Bakke 和Belich[19-21]提出的朗道型量子化理论,他们在LSV 背景下研究了自旋为 1/2 的中性粒子与磁场和电场组成的混合场的相互作用.另外,许多物理学家也在LSV 背景下研究了中性粒子与不同类型的势函数相互作用的情况,如反平方电势[22]和库仑型电势[23]等.LSV的应用还包括几何量子相位[24,25]和宇宙弦背景时空[26,27]等领域.
本文主要基于LSV 框架研究KG 方程描述的标量粒子的相对论量子效应.文献[28]分析了LSV 对KG 方程的影响.Vitória 和Belich[29]研究了KG 谐振子与LSV 产生的线性中心势的相互作用.因此,我们计划基于LSV,在存在和不存在磁场两种情况下研究康奈尔势函数在洛伦兹对称破坏框架中对广义KG 谐振子的影响.本文其他部分的主要内容如下:第2 节简要回顾LSV,并给出在LSV 背景下具有康奈尔函数的KG 谐振子方程;第3 节分别考虑康奈尔函数在有磁场和无磁场的情况下对KG 谐振子的作用;第4 节是结论.
2 洛伦兹对称破缺下的广义KG 谐振子
本节首先介绍洛伦兹对称破缺框架下的广义KG 谐振子,从标准模型扩展理论的角度来看,描述存在非最小耦合和电磁张量,且静止质量为m的相对论标量粒子的KG 方程为(ℏ=c=1)[29]

这里的电磁张量Fµν满足关系Fµν=∂µAν -∂νAµ,恒定的背景张量场来自于标准模型扩展理论之外的洛伦兹对称破缺,无量纲的张量系数是具有19 个独立非零分量的黎曼张量[30].此外张量系数κDE,κDB,κHE和κHB被定义为[31,32]
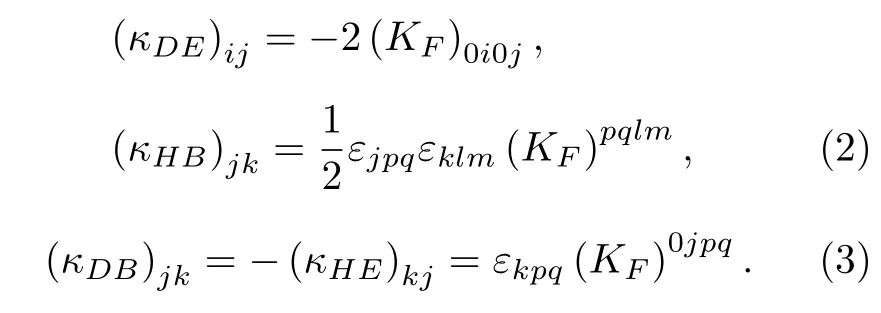
需要强调的是张量 (κDB)jk和 (κHE)kj是反对称矩阵,(κDE)ij和 (κHB)jk是对称矩阵.因此协变KG方程被重新表示为
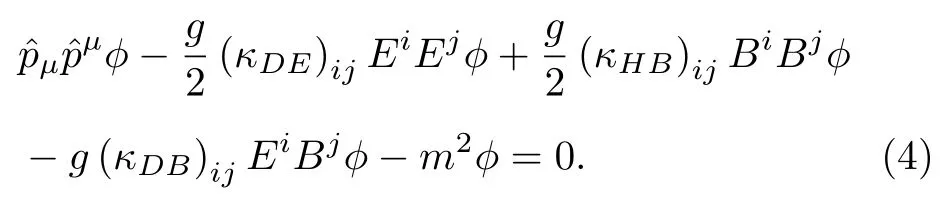
众所周知,KG 谐振子也被称为带有谐振子的KG场[1,2],通过非最小耦合,动量算符的相应变化如下:
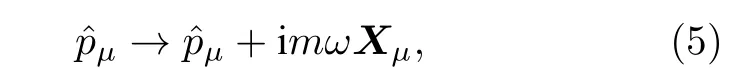
其中ω表示角频率.基于这一点,本文应用(1+3)维柱坐标形式下的闵可夫斯基时空度规
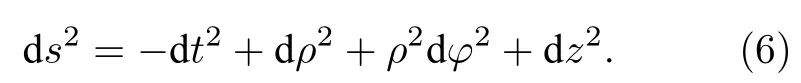
因此在考虑(5)式的作用后,(4)式中的KG 谐振子方程被重新写为
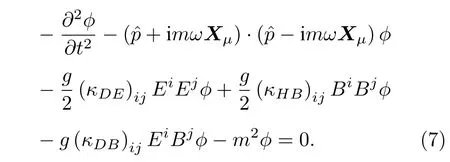
众所周知,KG 谐振子是通过考虑一个非最小耦合项的向量Xµ=(0,ρ,0,0,0)=ρρˆ 得出的,在这种情况下,用径向势函数f(ρ) 来代替ρ把KG 谐振子广义化,也就是

因此把(8)式代入(7)式,就可以得到如下二阶微分方程:
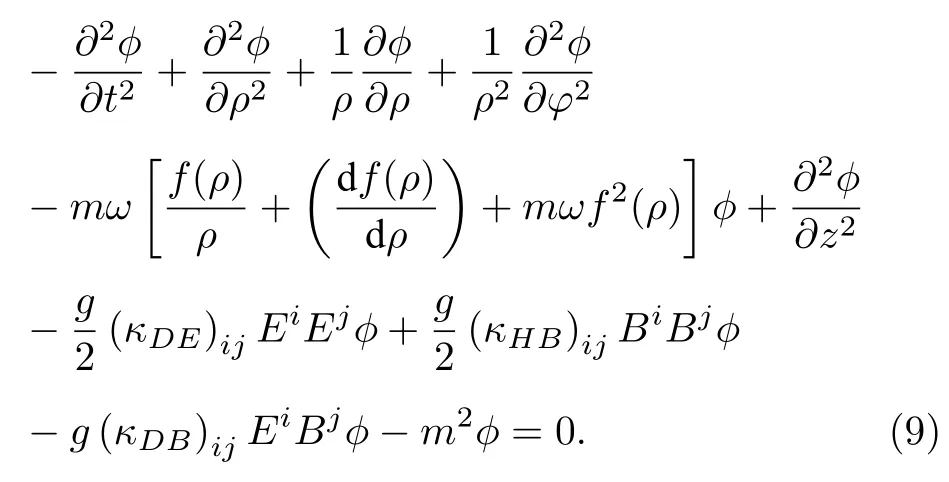
下面研究康奈尔势函数对广义KG 谐振子的影响,康奈尔势函数f(ρ) 可以写为
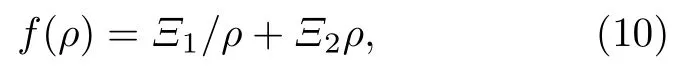
其中参数Ξ1和Ξ2分别表示规范理论中的库仑强度和弦张力.值得一提的是,康奈尔势在粒子物理学中有广泛的应用[33-36],它包含一个描述夸克和胶子相互作用的短程库仑势,以及一个长距离线性势.把(10)式代入(9)式可以得到

其中动量算符为=-i∂z,角动量算符为=-i∂φ.假设方程(11)的特解为
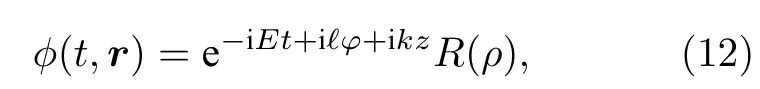
我们知道,径向波函数独立于坐标系的其他分量t,φ和z,(12)式中的ℓ=0,±1,±2,···是角动量算符的特征值,k是线性动量算符在z分量的特征值.
此时,把(12)式代入(11)式中得到
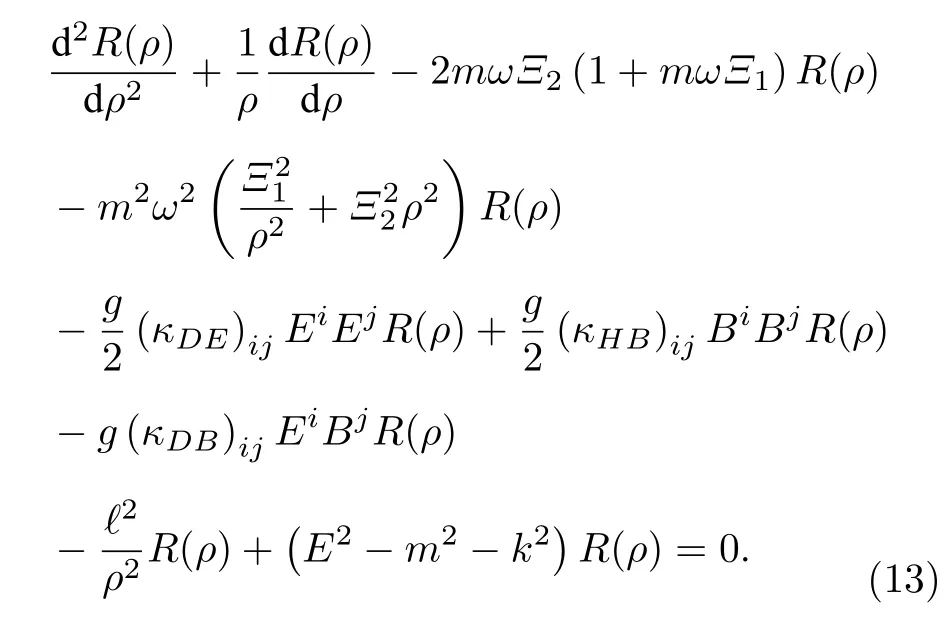
第3 节将研究在存在康奈尔势情况下洛伦兹对称破缺对广义KG 谐振子的影响.
3 洛伦兹对称破缺下广义KG 谐振子的能级与波函数

现在来求解方程(14)在两种不同情况下的能量本征值与束缚态波函数.
情况一不存在磁场,即B=0,此时待求解的方程(14)可被重新写为
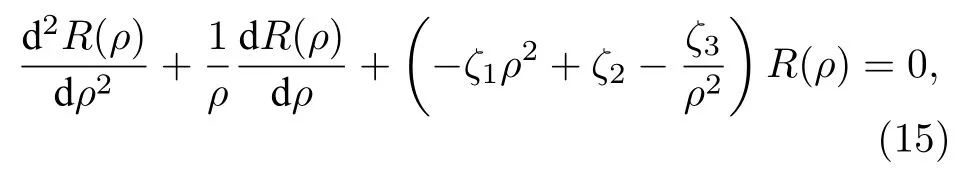
其中
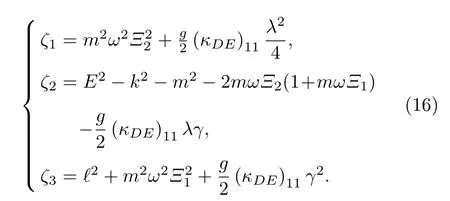
为了求解方程(15),令r=ρ2,则方程(15)变为
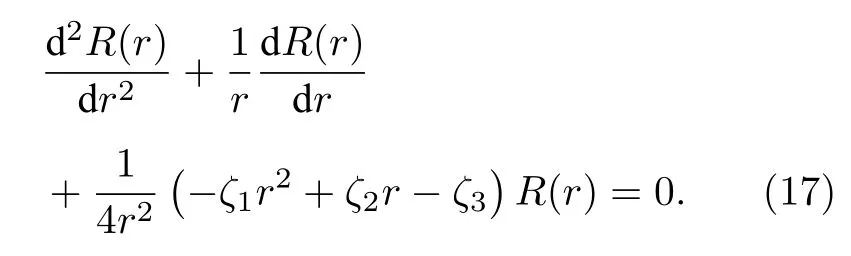
此时,可以发现波动方程与NU 方法[41,42]中的方程形式类似,Nikiforov-Uvarov (NU)方法对于求解量子理论中波动方程束缚态的精确解是非常有用的[43-48],NU 方法的详细说明见附录A.根据文献[48]结果,再依据附录A 中的NU 方法,可以得到波函数


将(19)式和(20)式代入(15)式,得到无磁场时洛伦兹对称破缺下KG 谐振子的非归一化径向波函数为

此外,为了更直观地反映不同λ值对波函数的影响,图1 给出了径向波函数R(ρ) 的图像.可以看出,在ρ →0 时径向波函数R(ρ) 的值为零,另外,径向波函数的振幅随着电场强度的增加而减少.通过系数关系
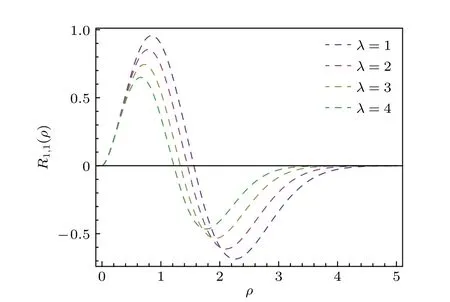
图1 以 ρ 为变量取4 个不同 λ 值的径向波函数Fig.1.Radial wave functions as a function of ρ for different λ .
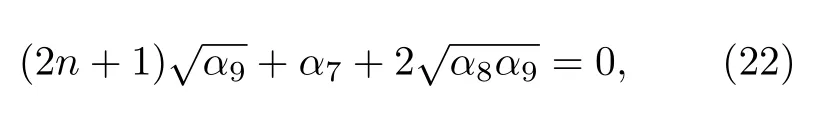
得到能量特征值为
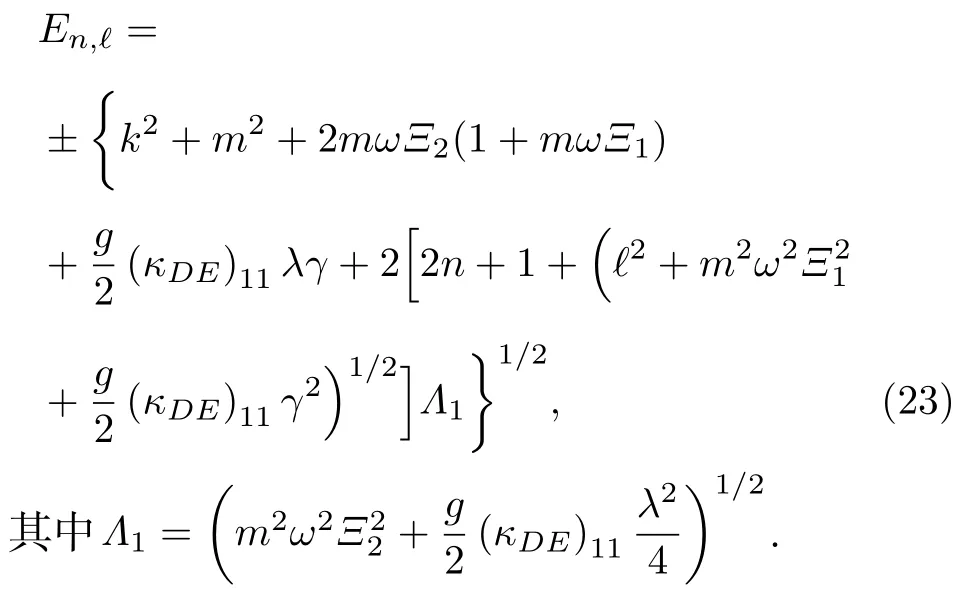
如果康奈尔势函数参数满足Ξ1=0,Ξ2=1,可以得到线性势作用下KG 谐振子的能量特征值为
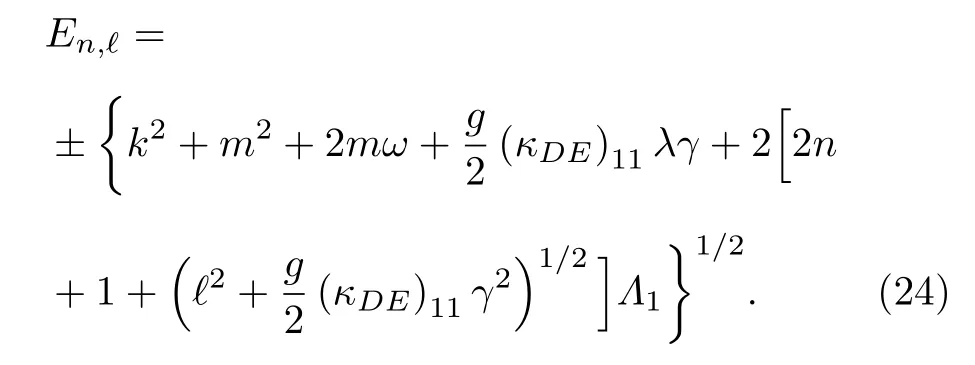
情况二 求解存在磁场B=B0的情况.方程(14)可重新写为

为了得到一个可解的波函数,令η=ρ2,则有

不难发现,方程(27)与NU 方程形式类似,所以同样利用NU 方法来处理这种情况.因此方程(27)的波函数可以假定为
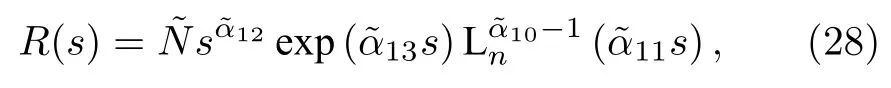
相关系数表示为
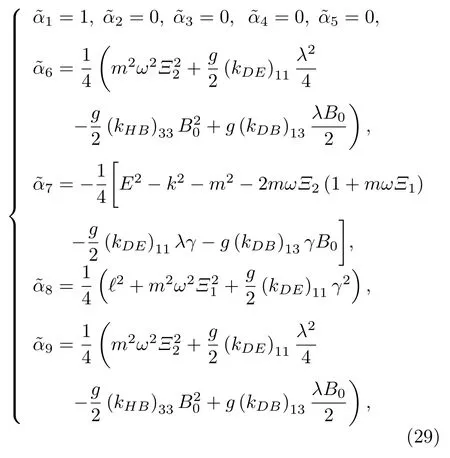
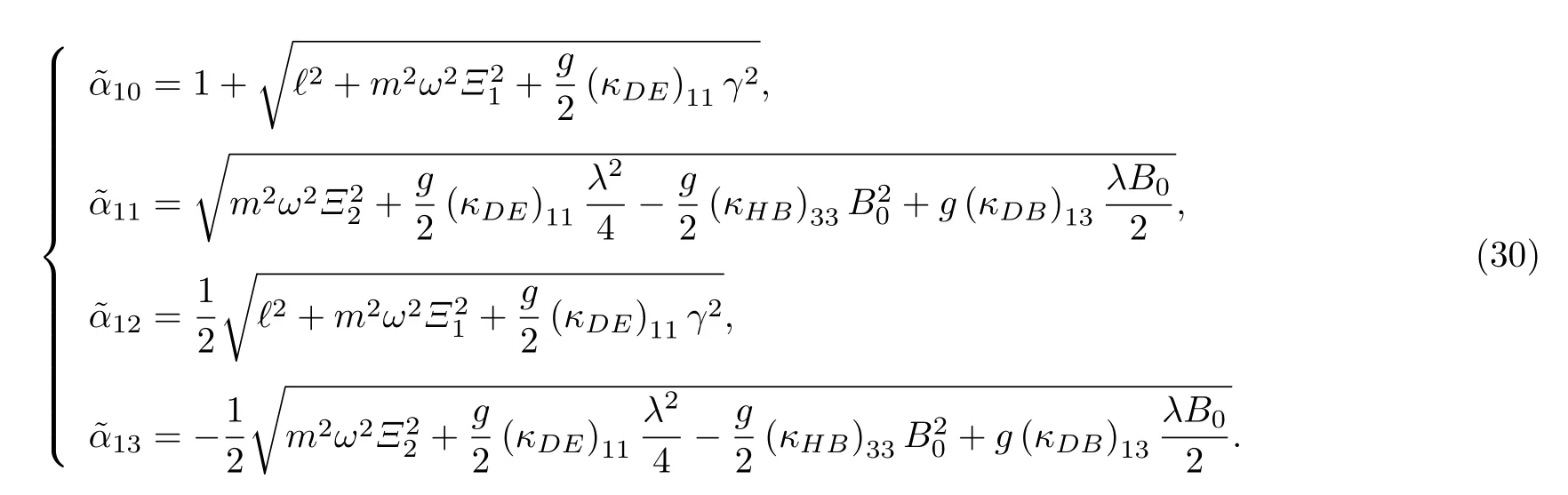
在洛伦兹对称破缺中具有康奈尔势函数且存在磁场情况下的广义KG 谐振子的非归一化径向波函数可以写为
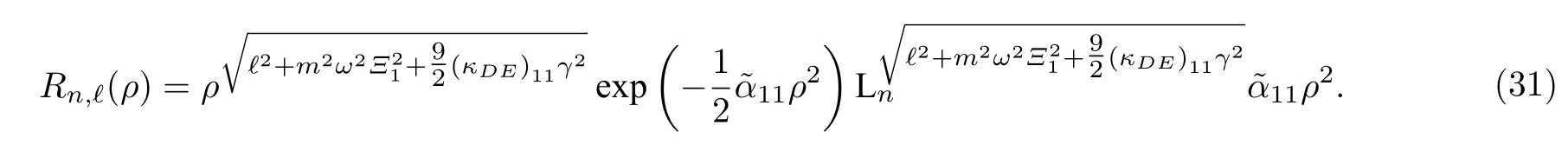
波函数(31)明显依赖于量子数l及图2 为非归一化的径向波函数R(ρ) 的图像,在图2中,令=(kDB)13=1,把ρ作为横坐标,画出了广义KG 谐振子在不同Ξ1值时的图像,能清晰地观察到径向波函数的振幅随着势函数参数的增加而增加.

图2 以 ρ 为变量取4 个不同1 值的径向波函数Fig.2.Radial wave functions as a function of ρ for different 1 .
根据系数关系
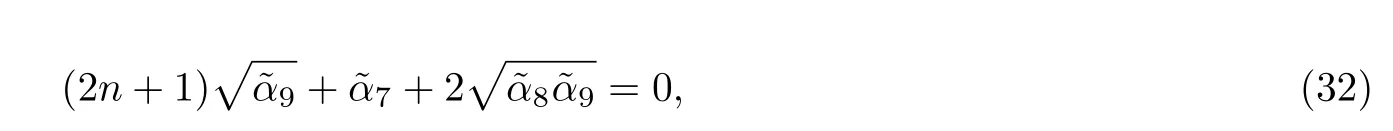
相应的能量特征值为
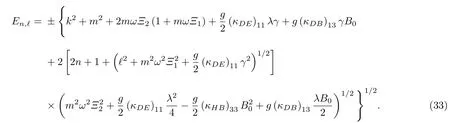

图3 以n 为变量取个不同 1 值的能量Fig.3.Energy eigenvalue as a function of n for different 1 .
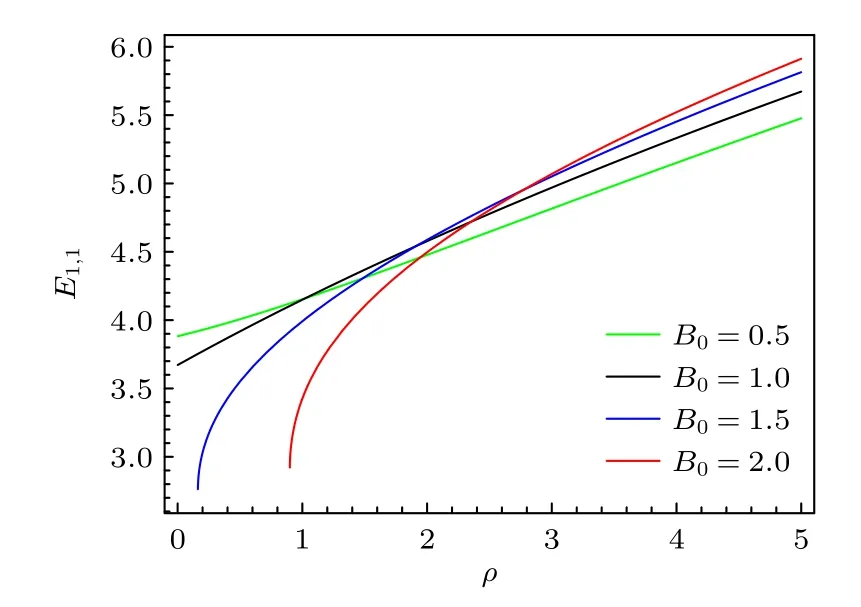
图4 以 λ 为 变量取4 个不同 B0 值的能量Fig.4.Energy eigenvalue as a function of λ for different B0 .
4 总结
本文研究了洛伦兹对称破缺框架下的广义KG谐振子,利用NU 方法分析了存在与不存在磁场时的广义KG 谐振子.此外还讨论了KG 谐振子在1的特殊情况.结果表明,存在磁场时的情况是无磁场情况的推广,因为当令B0=0时,束缚态能量特征值与无磁场时所得结果一致.两种情况下的径向波函数明显取决于洛伦兹对称破缺效应相关的参数和康奈尔势参数.此外,通过固定一些参数值,可以观察到在ρ→0 时径向波函数R(ρ) 的值也为零.另外,根据本文所画的图像得知,图1 中的径向波函数的振幅随电场强度的增加而减少,而图2 中的径向波函数的振幅随势参数的增加而增加.图3 显示了势函数参数对广义KG 谐振子能谱的贡献.可以看出,当固定量子数n时,较大的势函数参数对应着较大的能量特征值,而当固定势函数参数时,较大的量子数n所对应的能量特征值也相对较大.最后,发现在图4 中的能量特征值存在简并,同时在B0=1.5 和2 时,λ较小时能量特征值的增加趋势尤为显著.此外,从能谱的图像可以清晰地看到洛伦兹对称破缺的存在使得能谱得到了修正.
附录A Nikiforov-Uvarov 方法
本文利用NU 方法求解了二阶微分方程的本征函数,该方法有助于找到各种类薛定谔方程的特征值和特征函数,也可以用于一些涉及到二阶微分方程的其他物理背景中.在NU 方法中微分方程通常可以写成如下形式:

在NU 方法中微分方程的本征值通常通过如下方程给出:

其中涉及到的所有参数(α4···α13)都是通过α1,α2,α3和β1,β2,β3这6 个参数得到的:
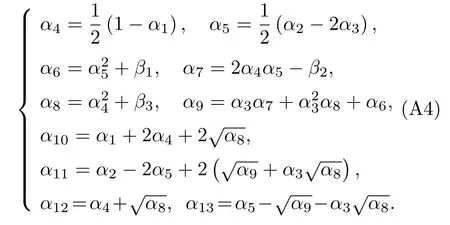
而α1,α2,α3和β1,β2,β3这6 个参数的值是可以通过微分方程(A1)直接确定的.
另外,对于α3=0 这种特殊情况有如下关系:

此时的波函数为


