极化敏感面阵的DOA-极化参数降维估计算法

刘淳熙，王文亮，彭冬亮*，陈志坤，吴美婵

(1.杭州电子科技大学 自动化学院，浙江 杭州 310018；2.中船(浙江)海洋科技有限公司，浙江 舟山 316021)

0 引言

随着电磁干扰和抗干扰技术的飞速发展，电磁环境日益复杂，电磁信号所蕴含的信息也越来越多[1-3]。普通阵列仅具有空域滤波能力，不能很好地区分期望信号和干扰信号，极化敏感阵列不仅能利用阵元间的相对空间位置进行空域滤波，还可以利用期望信号和干扰信号极化状态的差异在极化域滤波[4-6]，因此极化敏感阵列具有较强的抗干扰能力。

20世纪90年代以来，国内外学者对于极化敏感阵列的研究日益活跃，许多传统标量阵列的经典参数估计算法被推广到极化敏感阵列领域。

文献[7-8]利用旋转不变子空间(Estimation of Signal Parameters via Rotational Invariance Techniques，ESPRIT)算法实现了联合参数估计，但该方法需要对所估计的空间角度和极化参数进行额外配对，增加了计算量。文献[9]提出一种改进的ESPRIT算法，利用空域旋转不变关系得到6个旋转不变因子，通过数学运算得到一系列估计值，然后重构出多组对应的导向矢量，将其与噪声子空间一一正交检验，提取出正确的一组无模糊估计值，但算法运算复杂度较高，且ESPRIT类算法均对阵列结构有严格要求，不利于实际应用推广。文献[10]将MUSIC算法直接拓展到极化敏感阵列，通过多维搜索即可获得空域和极化域的参数信息。但是由于MUSIC算法需要进行谱峰搜索，同时对空域和极化域参数进行估计会使计算量急剧增大，因此有必要研究相关的降维算法。文献[11]提出了一种模值约束降维求根MUSIC算法，通过数学运算对波达角和极化参数进行剥离，先估计DOA信息，然后根据模值约束条件构造代价函数，通过闭式解求出极化参数。文献[12]提出一种恒模约束降维算法，对阵列接收矩阵用秩-1逼近恢复出信号的空域导向矢量和极化域导向矢量，然后估计出对应的参数。这些算法均能较为精确地估计出DOA和极化参数，但依然受到阵型的限制，仅适用于线阵或L阵。随着四元数模型在空间定位等领域的研究愈发广泛，一些学者将四元数模型与阵列参数估计算法相结合，提出了四元数MUSIC算法[13]、四元数求根MUSIC算法[14]以及降维四元数MUSIC算法[15]，将其应用到极化敏感阵列中。该方法虽然可以适当地降低一部分运算量，但无法精确估计极化参数。

实际工程中普遍应用二维面阵，现有的针对线阵或L阵的参数估计算法实际应用价值有限。因此本文提出了一种适用于极化敏感面阵的不等式约束降维MUSIC算法。在强噪声的多信源背景下，本算法能够较好地识别出信源的空域-极化域参数。算法首先利用Kronecker积的数学性质将极化域矢量与空域矢量分离，然后将四维联合谱估计问题转化为二元函数极值的求解，之后利用极化矢量的模值有界性构建不等式约束方程，得到空域参数估计值，同时将空间角度与约束方程结合得到极化参数估计。本算法大大降低了运算量，同时能够精确估计出DOA和极化参数。

1 阵列及其接收信号模型

本文研究极化敏感面阵，其阵元由双正交偶极子对构成，图1是由该阵元构成的M行N列的均匀面阵，图中的“黑色圆点”代表双正交偶极子。阵列摆放在XOY平面上，阵元间距d为半波长，即λ/2。定义俯仰角θ为与z轴正向的夹角，0≤θ≤π；定义方位角φ为顺时针与x轴正向的夹角，0≤φ<2π。

图1 极化敏感面阵结构Fig.1 Structure diagram of polarization sensitive array

假设空间中K个远场窄带信号入射到该面阵，其空间角度用(θk,φk),k=1,2,…,K表示，其中θk和φk分别表示第k个信号源的俯仰角和方位角。x轴和y轴上信号源的方向矢量分别为：

(1)

(2)

则阵列的空域导向矢量为[16]：

as(θk,φk)=ay(θk,φk)⊗ax(θk,φk),

(3)

式中，符号⊗表示Kronecker积。

电磁信号在空间中的传播如图2(a)所示，将信号的电场矢量E在两正交单位矢量eθ,eφ方向上分解，如图2(b)所示。

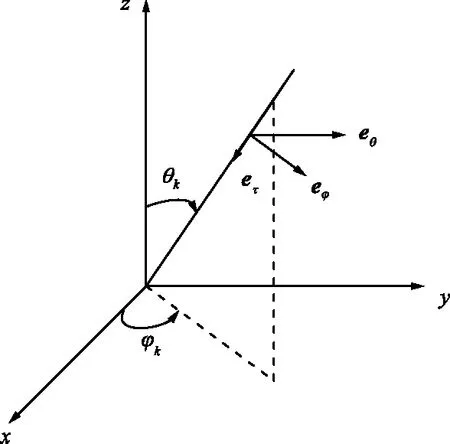
(a) 空间电磁信号传播

(b) 电场矢量分解图2 电磁信号传播与分解Fig.2 Electromagnetic signal propagation and decomposetion diagram

图2(b)中Vθ和Vφ为电场矢量E的2个分量，其中：

Vθ=sinγejη,Vφ=cosγ,

(4)

式中，γ∈[0,π/2]和η∈[-π,π]分别表示极化辅角和极化相位差，γ的正切值表示了eθ方向电场幅度与eφ方向电场幅度的比，η表示eθ方向电场与eφ方向电场的相位差。

在空间直角坐标系中，电场矢量E可以分解为：

E=Vθeθ+Vφeφ=

(Vθcosθcosφ-Vφsinφ)ex+

(Vθcosθsinφ+Vφcosφ)ey-(Vθsinθ)ez。

(5)

将矢量写成矩阵形式：

(6)

式中，γk,ηk分别表示第k个信源的极化辅角和极化相位差。本文所提阵列阵元为双正交偶极子对，仅能接收到与x轴和y轴平行的电磁波，则阵列的极化域导向矢量为：

(7)

因此阵列的极化域-空域联合导向矢量为：

a(θk,φk,γk,ηk)=ap(θ,φ,γ,η)⊗as(θk,φk)。

(8)

当K个远场窄带完全极化波入射到该极化敏感面阵时，阵列的接收数据x(t)可以写成下述形式：

AS(t)+N(t)，

(9)

式中，S(t)∈CK×1为入射信号矢量矩阵；N(t)∈C2MN×1为空-时-极化域白噪声矩阵；A∈C2MN×K为阵列流行矩阵：

A=[a1a2…ak…aK]，

(10)

式中，

ak=a(θk,φk,γk,ηk)。

(11)

根据式(9)所构建的信号模型，对K个目标的二维空间角度和二维极化角度进行估计的过程称为极化域-空域联合谱估计。

2 极化域-空域联合估计算法

2.1 四维MUSIC算法

(12)

式中，X=AS+N为P次快拍的接收数据矩阵。

对其进行特征值分解得到：

(13)

式中，US表示K个较大特征值所对应的特征向量构成的信号子空间；UN表示2MN-K个较小特征值所对应的特征向量构成的噪声子空间。

通过分析可知，信号子空间与阵列的导向矢量张成的空间是同一空间，信号子空间与噪声子空间相互正交[17]，则阵列的导向矢量与噪声子空间也正交，即：

aH(θk,φk,γk,ηk)UN=0,k=1,2,…,K。

(14)

考虑到实际接收数据矩阵是有限长的，且实际接收数据矩阵中混有噪声，因此a(θ,φ,γ,η)与UN不完全正交，即式(14)不完全成立，实际上求DOA是以最小优化搜索实现的，即四维联合谱函数定义为：

(15)

遍历θ,φ,γ,η四个参数，找出谱函数最大的K个峰值对应的方位角、俯仰角、极化辅角和极化相位差即为K个来波信号的参数估计值。

该传统MUSIC算法需要进行四维全局谱峰搜索，运算量极大，难以实现。本文利用极化参量模值的有界性，引入不等式约束将四维谱峰搜索降低至二维，先行估计二维空域参数，进而得到极化参数。

2.2 基于不等式约束优化的降维MUSIC算法

结合式(7)和式(8)，把阵列导向矢量写成仅包含空域参数的矢量和仅包含极化域参数的矢量的乘积形式：

Γ(θk,φk)σ(γk,ηk),

(16)

式中，

(17)

(18)

则式(15)谱函数可以改写成：

PMUSIC(θ,φ,γ,η)=

(19)

分析式(18)可知极化参数矢量σ(γ,η)的模值有如下关系：

(20)

令:

(21)

则四维谱函数的谱峰搜索过程可以转化为在不等式约束条件下的极值求解问题：

(22)

从四维谱峰搜索转换到不等式约束条件下的极值求解过程的证明过程可参见文献[18]，其中定义检测量为:

(23)

令:

(24)

以am(β)为待求解变量，对式(23)进行角度估计可转化为求解以下优化方程：

(25)

式中，e1=[1,0,…,0]T。本文中用σ(γk,ηk)和Γ(θk,φk)分别替换式(23)中的am(β)和[an(α)⊗IM]，以σ(γk,ηk)为待求解变量，相应改变对其模值的约束条件即可将式(19)的四维谱峰搜索问题转化为式(22)所示的优化方程求解问题。

构造代价函数：

L(θ,φ,γ,η,λ,ω)=σ(γk,ηk)HV(θ,φ)σ(γk,ηk)-

λ(‖σ(γk,ηk)‖2-3+ω2),

(26)

式中，λ是拉格朗日乘子;ω是新引入的松弛变量，目的是为了将不等式约束经过松弛后变为等式约束。对式(26)求导，并令结果为零：

(27)

进一步化简得：

V(θ,φ)σ(γk,ηk)=λσ(γk,ηk)。

(28)

(29)

对应求解即可得到第k个信源的极化参数估计值。

2.3 复杂度分析

本节对4D-MUSIC算法和本文所提的RD-MUSIC算法的计算量进行比较分析，2种算法均选用图1所示的阵列结构，竖直和水平阵列参数分别为M和N，入射信号数为K，快拍数为L，搜索的角度点数为n。

对于4D-MUSIC算法，求阵列接收信号自相关矩阵计算量为O{L(2MN)2}，矩阵特征值分解计算量为O{(4MN)3}，四维角度搜索计算量为O{n4(4MN+1)(4MN-K)}，总计算量为O{L(2MN)2+(4MN)3+n4(4MN+1)(4MN-K)}。

本文所提降维MUSIC算法计算自相关矩阵和获得特征值分解的计算量与4D-MUSIC算法相同，角度搜索时先对二维空间角度进行搜索，后对二维极化角度搜索，计算量为o{n2(16MN+4)(4MN-K)} ，总计算量为o{L(2MN)2+(4MN)3+n2(16MN+4)×(4MN-K)}。

图3给出了信源数L=2，分别采用1°粗搜索和0.1°精搜索时，4D-MUSIC算法和本文算法计算量随着阵元数变化的对比关系。

图3 2种算法复杂度对比Fig.3 Complexity comparison of two algorithms

为了更直观地看出本文算法在运行时间上的优势，表1给出了4D-MUSIC算法和本文算法的运行时间随着阵元数变化的对比关系。

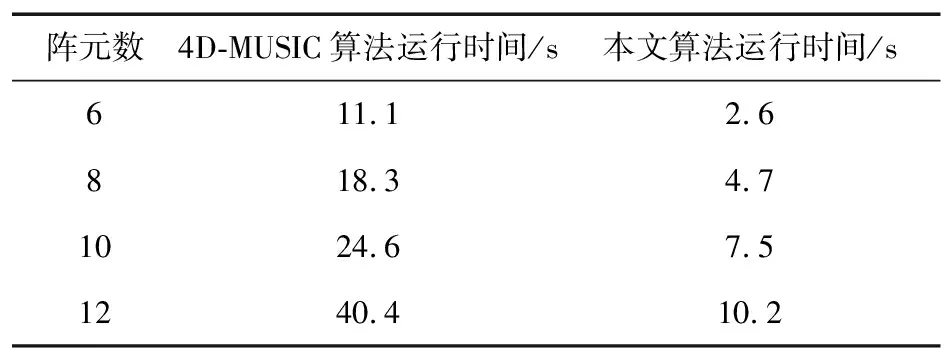
表1 4D-MUSIC算法和本文算法的运行时间随着 阵元数变化的对比关系

由图3和表1可见，本文提出算法的复杂度实际上远低于MUSIC算法的复杂度。这是因为在算法运行过程中M,N,K和L远远小于n，传统MUSIC算法的运算量为n4量级，而本算法运算量为n2量级，运算量大大降低。

3 仿真实验

本节用计算机仿真来验证本文所提算法的准确性及有效性。仿真所用阵列结构如图1所示，阵元数M=4,N=2，阵元间距为λ/2。

仿真1目标DOA与极化参数估计

考虑2个非相干信号入射到阵列，信号俯仰角为θ=[5°,20°]；方位角φ=[10°,50°]；极化辅角γ=[30°,45°]；极化相位差η=[60°,80°]。快拍数snap=1 000，信噪比SNR=20 dB。图4给出了空域参数的MUSIC谱图像，图上显示出2个清晰可辨的峰值，说明本算法能够正确估计出目标的二维空间参数。图5和图6分别给出了本算法所估计出的二维空间角度和二维极化角度的坐标图。从图6看出，本算法也能够对极化参数进行较为精准的估计。

图4 空域MUSIC谱Fig.4 Spatial MUSIC spectrum

图5 方位角与俯仰角坐标Fig.5 Coordinates of azimuth and elevation angle

图6 极化辅角和极化相位差坐标Fig.6 Coordinates of polarization auxiliary angle and polarization phase difference

仿真2算法性能与信噪比关系

本仿真对比了传统的4D-MUSIC算法和本文算法的空域、极化域参数估计性能。蒙特卡罗次数L为500，信噪比从-10 dB变化至20 dB，用均方根误差(Root Mean Square Error,RMSE)评估算法的空域和极化域参数估计性能，实验中RMSE计算如下：

(30)

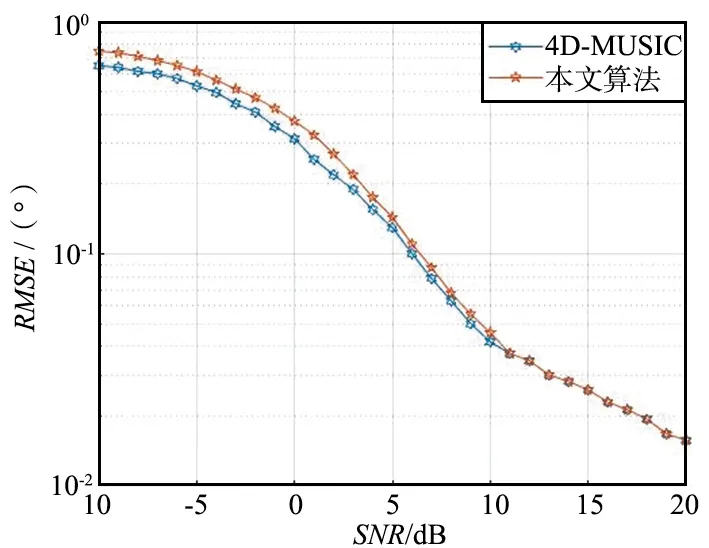
图7 DOA参数的RMSE随SNR变化曲线Fig.7 RMSE curve of DOA parameters varied with SNR

图8 极化参数的RMSE随SNR变化曲线Fig.8 RMSE curve of polarization parameters variedwith SNR

4 结束语

本文首先建立了一种适用于均匀平面阵列的长矢量接收信号模型，然后提出了一种适用于该阵列的空域-极化域联合估计算法。该算法利用极化矢量范数的有界性，将四维联合谱搜索过程转化为二维的约束优化问题，在估计精度基本不变的情况下显著降低了计算量。仿真实验证明算法在较低信噪比条件下仍能得到较高精确度的估计值。